Rep:Mod:SHMod3Phys
Stuart Haylock - Computational Lab - Module 3 - Physical Computational Chemistry Experiments
Aim:
The aim of this experiment is to characterise transition structures on potential energy surfaces for both the Cope rearrangement and the Diels Alder cycloaddition reactions. In these calculations, instead of using molecular orbital-based methods, I will be numerically solving the Schrödinger equation to locate transition structures.
The Cope Rearrangement
In this section I will be finding the energy minima of the transition structures within the Cope rearrangement (above). The Cope rearrangement is a [3,3]-sigmatropic shift and has numerous computational studies[1].
The first optimisation of 1,5 hexadiene with an "anti" linkage was done with the HF/3.21G level.
| File Name | Anti |
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RHF |
| Basis Set | 3-21G |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -231.69253522 a.u. |
| RMS Gradient Norm | 0.00002849 a.u. |
| Dipole Moment | 0.0000 Debye |
The symmetry of this molecule is Ci.
The second optimisation of 1,5 hexadiene with an "gauche" linkage was done with the HF/3.21G level.
| File Name | Gauche |
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RHF |
| Basis Set | 3-21G |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -231.68771616 a.u. |
| RMS Gradient Norm | 0.00000491 a.u. |
| Dipole Moment | 0.4556 Debye |
The symmetry of this gauche molecule is C2.
From this you can see that the anti conformation is the lowest in energy, although the gauche conformation is close in energy this may be due to secondary orbital interactions inducing a stabilisation effect ("gecko effect") and therefore lowering the energy of this conformation.
According to the conformation table in the instructions page[2] the molecules I have sketched are the Gauche 1 conformer and the Anti 2 conformer, judging by the energy, symmetry groups and the general design of the molecule.
As my anti hexadiene molecule already has a Ci symmetry group I then reoptimised the structure with a B3LYP/6.31G level which the following summary output.
| File Name | DFT Anti |
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -234.55970424 a.u. |
| RMS Gradient Norm | 0.00004654 a.u. |
| Dipole Moment | 0.0000 Debye |
Which still has a Ci point group. With the more accurate basis set and method you can see that the energy has decreased relatively substantially although there is almost no visible difference in the geometry of the molecule itself.
From the frequency analysis you can see there are no imaginary vibrations which means the molecule has optimised correctly.
| Values | |
|---|---|
| Sum of electronic and zero-point energies | 234.416244 |
| Sum of electronic and thermal energies | 234.408954 |
| Sum of electronic and thermal enthalpies | 234.408010 |
| Sum of electronic and thermal free energies | 234.447849 |
When these values are compared with literature[3] you can see a very good agreement with the experimental data with respect to energetic stability showing that this computed structure is practically the same as a experimental molecule.
Optimisation of the "Chair" and "Boat" transition structures
By computing the force constants for a reaction and using a specific coordinates for the transition structure bonds you can optimise a transition structure, and you can also calculate the activation energies.
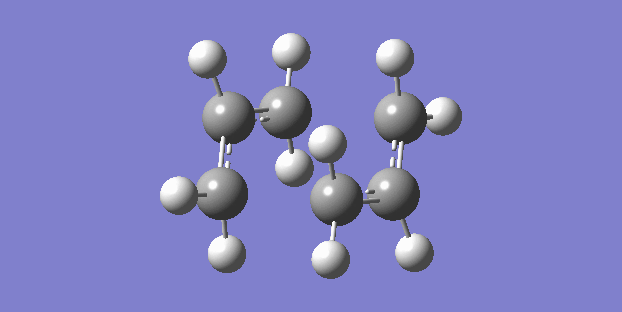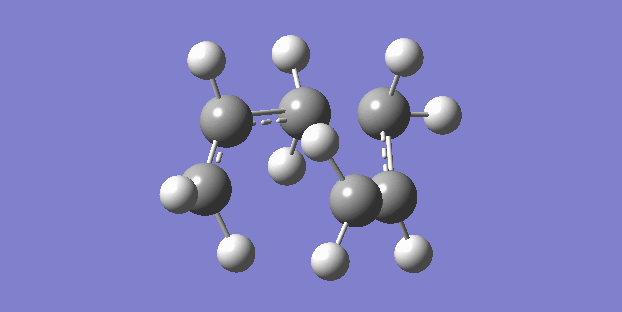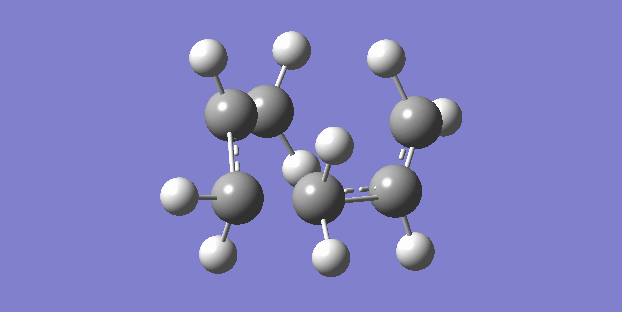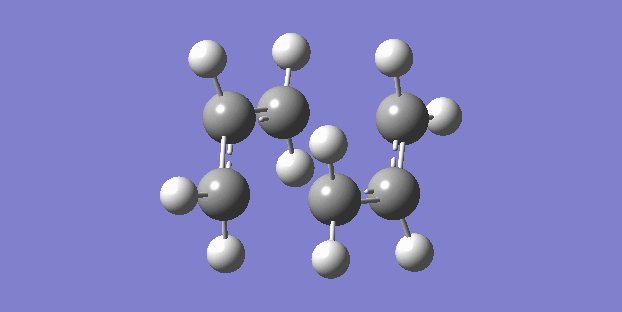The chair structure is the first that was sketched and optimised. The frequency calculation showed just one vibration which corresponded to the cope rearrangement. (right)
References
- ↑ Houk et al.,DOI:10.1021/ja00101a078
- ↑ https://www.ch.ic.ac.uk/wiki/index.php/Mod:phys3#Appendix_1
- ↑ E. Ventura, S. Andrade do Monte, M. Dallos, H. Lischka, J. Phys. Chem. A, 2003, 107 (8), pp1175-1180. DOI:10.1021/jp0259014