Rep:Mod:SG1994
Introduction
The transition state structure of a reaction is the structure which corresponds to the highest free energy along the reaction coordinate. The reactants must reach this structure (and energy) in order to form the products. Although transition structures cannot be isolated and studied directly in the laboratory they can be computed using a program and from there, the energies and geometries of these structures can be determined. Gaussview05 is used in this experiment to locate transition structures in the Cope Rearrangement of 1,2-hexadiene as well as in two Diels-Alder cycloaddition reactions.
Two different levels of theory were used in this experiment: the HF/3-21G and the B3LYP/6-31G(d); the latter being the more accurate level. It is usual to optimise first with the lower level of theory before using the higher as it shortens calculation time if the structure has already been roughly optimised.
The different methods used to calculate these transition structures were:
- Calculating the force constants using a guess structure that resembles the actual transition structure
- Using the redundant coordinates method to optimise the structure before locating a transition state
- The QST2 method where the transition structure is found through interpolation of the reactants and products
Opt+Freq optimisations were also run, where the vibrational frequencies of the transition structures can be determined as well as the thermochemical data required to calculate the corresponding activation energies. A frequency analysis calculates the second derivative of the potential energy plot and so the vibrational frequencies of a transition structure should be imaginary (negative) as it is a maximum on the plot.
Nf710 (talk) 13:59, 19 November 2015 (UTC) It would have been nice here if you could have included some understanding of the differences between the HF and DFT methods. such that HF uses slater determinants and a mean field for e-e repulsion and DFT uses functionals of the electron density
The Cope Rearrangement of 1,5-Hexadiene
Background

|
| The Cope Rearrangement |
The Cope Rearrangement is a concerted pericyclic reaction involving the [3,3] - sigmatropic rearrangment of 1,5-dienes [1]. The rearrangement can go via a boat or chair transition structures, both of which are structurally equivalent to diradicals [2]. In this experiment, 1,5-hexadiene will be used as an example to locate low-energy conformers ("anti" and "gauche" structures) as well as the transition structures involved in the rearrangement.
The reactants and products were first built and optimised before locating the transition states using the three methods mentioned in the background.
Optimising the Reactants and Products of 1,5-Hexadiene
HF/3-21G level of theory
The conformers of 1,5-hexadiene were built, cleaned and optimised using the HF/3-21G level of theory on Gaussview05.
The first conformer built was one with an "anti" linkage for the central four atoms as shown in Fig1. After cleaning and optimising, the energy was found to be -231.69253528 hartrees and the point group Ci. The log file for this optimisation can be found here.

This was found to be the anti2 molecule found in Appendix 1 of the script where its energy was calculated to be -231.69254 hartrees with also a point group symmetry of Ci. In comparison to Appendix 1, the energy of the structure is identical up to at least 6 d.p..
The second conformer built was one with a "gauche" linkage for the central four atoms (shown in Fig2).
The energy of this conformer is expected to be of higher energy than the anti2 molecule above due to the increased unfavourable interaction between the two largest substituents connected to the middle two carbon atoms. After cleaning and optimising, the energy was found to be -231.69153035 hartrees, supporting the theory of increased repulsion, and the point group C2. This molecule corresponds to the gauche4 molecule in Appendix 1 and the optimisation log file can be found here.
The lowest energy conformer was expected to be anti2 due to the antiperiplanar arrangement of the two largest substituents. However, the gauche3 molecule (Fig3) from Appendix 1 was found to be the lowest energy conformer.

After optimising, this conformer was found to have a point group of C1 and its energy was calculated to be -231.69266122 hartrees and the log file can be found here.
Nf710 (talk) 15:17, 19 November 2015 (UTC) You havent mentioned why the gauche 3 has the lowest energy. You could have shown this by looking at the orbitals in the .chk clearly showing favourable secondary orbital overla.
B3LYP/6-31G(d) level of theory
The anti2 molecule was then optimised using the B3LYP/6-31G(d) method - a higher level that produces a structure that is more representative of the experimental structure compared to the HF method.

The energy calculated using this method is -234.61171063 hartrees - lower than the energy when using the 3-21G method indicating the formation of a molecule which is more representative of the exact molecule. The optimisation log file can be found here.
Nf710 (talk) 15:20, 19 November 2015 (UTC) Correct energy
Frequency analysis was also performed on this molecule using the B3LYP method and the frequency log file can be found here. An absence of imaginary frequencies in this molecule confirms the successful optimisation to a minimum.
While both the structures of anti2 have a symmetry of Ci, the bond lengths differ slightly as compared in the table below.

| Bond lengths (Å) | ||
|---|---|---|
| Atoms | HF/3-21G | B3LYP/6-31G |
| C1-C2 | 1.31613 | 1.33350 |
| C2-C3 | 1.50891 | 1.50419 |
| C3-C4 | 1.55275 | 1.54816 |
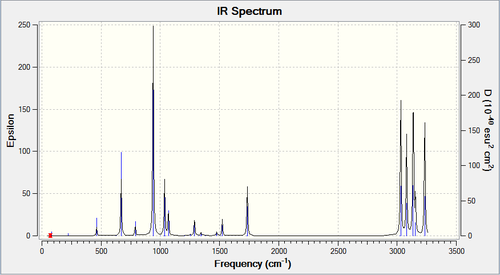
Above shows the vibrational frequencies of anti2.
Nf710 (talk) 15:22, 19 November 2015 (UTC) Nicely tabulated, however you havent shown dihedrals or really commented on the geoms that much. You also havent mentioned the thermochemistry data.
Optimising the "Chair" and "Boat" Transition Structures
1,5-hexadiene can undergo the Cope rearrangement via two different transition structures: the chair and the boat which can be seen below.
 |
 |
| Chair TS | Boat TS |
Three different methods were used to locate the transition structures of the Cope rearrangement of 1,5-hexadiene. These were: by computing force constants; using the redundant coordinate method; and using the QST2 method.
An IRC (Intrinsic Reaction Coordinate) method is also used to locate a transition state at its local minimum.
Computing Force Constants Method

An allyl fragment was drawn and optimised using the HF/3-21G level of theory. Two of these fragments were oriented in a chair arrangement approximately 2.0 Å apart with a point group symmetry of C2h to form a guess transition structure.
By using a Opt+Freq method to optimise to a transition structure (Berny) and choosing to calculate the force constants once allows the transition structure to be located provided that the calculation is ran on a structure that is close to the TS.
The transition structure generated has an energy of -231.61932187 hartrees with an imaginary frequency of magnitude 817.99 cm-1 found corresponding to the Cope rearrangement (see below), confirming the successful location of a transition state structure. The log file can be found here.
The terminal carbon (bond forming/breaking) distances were calculated to be 2.02138 Å.
Chair TS Vibration |
Nf710 (talk) 15:27, 19 November 2015 (UTC) It would have been nice here if you could have talked about why the frequencies are imaginary. It comes from the quantum harmonic oscillator and the 2nd derivative of the PES (force constant)
Redundant Coordinate Method
This method is useful when the guess transition structure is not representative of the actual structure. By first freezing the reaction coordinate - the bonds that are partially formed in the TS - and minimising the rest of the molecule before optimising to a transition state, the structure can be located.
The guess transition structure is optimised again, but to a minimum and with the terminal carbons frozen at a distance of 2.2 Å using the Redundant Coord Editor. This resulting structure is then reoptimised to a TS (Berny), finding the derivative of the terminal carbon bond lengths. The bond forming lengths were calculated to be 2.02074 Å; shorter than that calculated using the force constants method and thus further proving a more stable transition structure.
An imaginary frequency of magnitude 817.89 cm-1 (shown above) corresponding to the Cope rearrangement was found.The similarity of the frequencies using both methods show they have both produced transition structures are essentially the same. The log file can be found here.
QST2 method
The boat transition structure was optimised using this method, where the reactant and products are specified and the calculation locates the structure at the energy maximum between the two. The atoms were labelled as shown below.
 |
 |
The Opt+Freq method was used to optimise the structure to a transition structure (QST2) at the HF/3-21G level of theory. The resulting transition structure is a rather distorted one, not one resembling that of a boat.
The log file can be found here.
The structures of the reactants and products were modified by rotating the central C-C bond to closer resemble the boat structure before running the calculation again.
 |
 |
The boat structure has been successfully located and the log file can be found here. An imaginary frequency corresponding to the Cope rearrangement (shown below) was found of magnitude 840.04 cm-1.
Boat TS Vibration |
IRC Calculation
The Intrinsic Reaction Coordinate (IRC) calculation finds the local minimum of a transition state by recording points along the reaction coordinate. Increasing the number of points recorded allows more geometries to be considered and so the accuracy of the structure located is increased.
In this example, the chair transition structure was used and as the reaction coordinate is symmetrical, it is computed in the forward direction only. 50 points were found to be sufficient in finding the local minimum and the log file can be found here.
 |
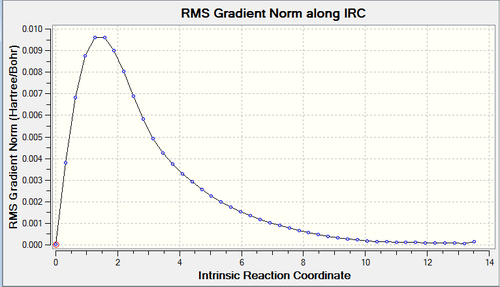 |
The IRC plot (left) shows the optimisation of the chair transition structure to a minimum while the RMS plot (right) is the derivative of the IRC plot. Reaching 0 on the RMS plot shows the successful optimisation to the structure of minimum energy.
Nf710 (talk) 15:31, 19 November 2015 (UTC) Nice IRC however you ahvent tried to find the structure that it connects. you could have done this by looking at the energy
Activation energies
Activation energies for the reaction are calculated for both the 3-21G and 6-31G(d) levels of theory. This is done by finding the energy difference between the anti2 reactant and the chair/boat transition structures.
Both the chair and boat transition structures obtained using the HF/3-21G method were used to run an Opt+Freq calculation on at the B3LYP/6-31G level of theory.
The chair log file can be found here and the boat here.
The chair has an imaginary frequency of magnitude 565.64 cm-1 and the boat 530.36 cm-1 confirming the generation of transition structures.
| Bond forming lengths (Å) | ||
|---|---|---|
| HF/3-21G | B3LYP/6-31G | |
| Chair TS | 2.02073 | 1.96767 |
| Boat TS | 2.13988 | 2.20664 |
While both the chair transition structures have very similar geometries (point groups: C2h as well as the two boats (point groups: C2v) the energies of these structures are very different. These energies are compared in the results table below.
Results Tables
| HF/3-21G | B3LYP/6-31G(d) | |||||
|---|---|---|---|---|---|---|
| Electronic energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | Electronic energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | |
| At 0 K | At 298.15 K | At 0 K | At 298.15 K | |||
| Chair TS | -231.619322 | -231.466705 | -231.461346 | -234.556982 | -234.414929 | -234.409008 |
| Boat TS | -231.619322 | -231.466699 | -231.461340 | -234.543093 | -234.402342 | -234.396008 |
| Reactant (anti2) | -231.692535 | -231.539539 | -231.532565 | -234.611711 | -234.469219 | -234.461869 |
The thermochemical data found in the log files for the reactant and transition structures are shown in the table above, with 1 hartree = 627.509 kcal/mol.
| HF/3-21G | B3LYP/6-31G(d) | Expt. | |||
|---|---|---|---|---|---|
| At 0 K | At 298.15 K | At 0 K | At 298.15 K | At 0 K | |
| ΔE (Chair) | 45.70 | 44.69 | 34.07 | 33.17 | 33.5 ± 0.5 |
| ΔE (Boat) | 41.97 | 41.33 | 45.71 | 44.69 | 44.7 ± 2.0 |
Using the higher level of theory has generated structures closer to the experimental values which shows a more representative structure.
Nf710 (talk) 15:41, 19 November 2015 (UTC) Your boat energy looks like it is slightly wrong. hence you at about 0.2 out on your activation energy. good comparison of geometries.
Nf710 (talk) 15:41, 19 November 2015 (UTC)In general this is a good report, you have done everything that has been asked out you (pretty much) however you haven't included any theory or understanding of the methods such as DFT or HF and you haven't shown any understanding of what happens in an optimisation.
The Diels-Alder Cycloaddition
(If you're going to use a different method, it's best to first use the script method and then compare with your method if you have time (AM1 and HF). This is only because you can end up with the wrong results and conclusions Tam10 (talk) 17:44, 12 November 2015 (UTC))
Background
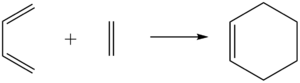 |
| Diels-Alder cycloaddition between cis-butadiene and ethylene |
The Diels-Alder reaction is a [4+2]-cycloaddition between a conjugated diene and a dienophile. The overlap of dienophile and diene π-orbitals result in the formation of σ-bonds in place of the π-bonds[3]. The reactions studied were: ethylene with cis-butadiene; and cyclohexa-1,3-diene and maleic anhydride.
Cis-butadiene and ethylene
Reactants
Cis-butadiene was then optimised to a minimum using using the HF/3-21G level of theory. The molecule has an energy of -154.05394317 hartrees and the log file can be found here.
 |
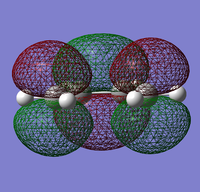 |
The HOMO of cis-butadiene is symmetric (s) while the LUMO is anti-symmetric (a).
Ethylene was built and optimised to a minimum the same method as for cis-butadiene. The log file can be found here. Its energy was calculated to be -77.60098811 hartrees and its HOMO and LUMO was visualised using Gaussview05 (see below).
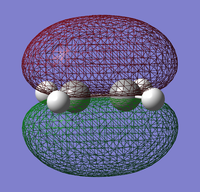 |
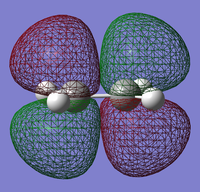 |
It can be seen that the HOMO of ethylene is anti-symmetric (a) while the LUMO is symmetric (s) with respect to the plane.
This indicates that it is the HOMO-LUMO interaction between the two molecules in the Diels-Alder cycloaddition.
Transition structure
The two reactants were placed 2.2 Å apart and optimised to a transition state (Berny) using the HF/3-21G level of theory. The transition structure generated has an energy of -231.60320857 hartrees with a terminal carbon distance of 2.20959 Å. The log file found here shows that there is an imaginary frequency of magnitude 818.34 cm-1 which corresponds to the DA cycloaddition.
|
|
The imaginary vibration is synchronous and can be seen that it is involved in the bond formation in the transition structure, whereas the vibration on the right hand side (lowest positive frequency) is not involved in the formation of bonds in the transition structure.
The typical sp3 and sp2 C-C bond lengths are 1.54 and 1.34 Å respectively [4] and the van der Waals radius of carbon is 1.70 Å [5]. The bond forming lengths in this structure are 2.21 Å, which is shorter than double the van der Waals radius, indicating an attractive interaction between the two reactants in the transition structure.
The HOMO of the transition structure. which can be seen below, is anti-symmetric with respect to the plane.
 |
 |
(Using AM1 you would see that the HOMO is antisymmetric Tam10 (talk) 17:44, 12 November 2015 (UTC))
The MOs involved in forming these transition structure MOs are the HOMO of cis-butadiene with the LUMO of ethylene and vice versa. This is an allowed reaction due to the MOs being of the same symmetries. According to the Woodward-Hoffman rules these reactions will be a 4πs+2πs reaction or a 4πa+2πa; both of which are thermally allowed reactions.
Results Tables
| HF/3-21G | |||
|---|---|---|---|
| Electronic energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | |
| At 0 K | At 298.15 K | ||
| TS | -231.603209 | -231.451339 | -231.445651 |
| Cis-butadiene | -154.053943 | -153.962189 | -153.958406 |
| Ethylene | -77.600988 | -77.545906 | -77.542948 |
Above is the thermochemical data of the reactants and products.
The activation energies at the HF/3-21G level of theory were calculated below.
| HF/3-21G | ||
|---|---|---|
| At 0 K | At 298.15 K | |
| ΔE | 35.614900 | 34.954134 |
The activation energy is lower at 298.15 K, this may be due to the increase in temperature providing more kinetic energy to the reactants, and thus being closer in energy to the transition structure.
Cyclohexa-1,3-diene and maleic anhydride
Reactants and products
Both cyclohexa-1,3-diene and maleic anhydride were built separately on Gaussview05 and optimised to a minimum using the HF/3-21G level of theory.
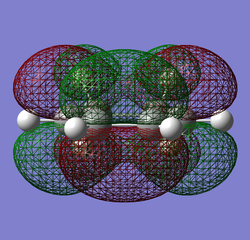
The energy of cyclohexa-1,3-diene was calculated to be -230.476524789 hartrees and its point group C2v. The log file for this optimisation can be found here.
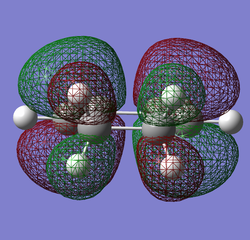 |
 |
The log file for maleic anhydride, with a calculated energy of -375.10351286 hartrees and with a point group of C2, can be found here.
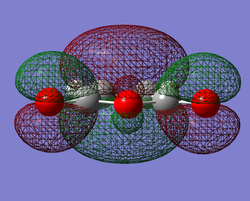 |
 |
The exo product was built by stacking the two optimised reactants (at a distance of 1.6 Å) with the C=O groups facing away from the double bond that is formed in the Diels-Alder cycloaddition. Bonds were formed and broken to resemble the product. This structure was optimised to a minimum at the HF/3-21G level of theory and its log file can be found here. It can also be seen here that it is the HOMO-LUMO intereaction that is allowed for the Diels-Alder reaction.
The endo product was generated in the same way as the exo but instead, with the C=O groups tucked under the diene (overlapping with the double bond formed in the product). Its log file can be found here.
Transition structures
The transition structures were located using the QST2 method. The exo TS log file can be found here and the endo TS log file can be found here.
The exo transition structure has an energy of -605.60359125 hartrees and the endo -605.61036819 hartrees, as visualised below.
|
|
Both of these imaginary frequencies corresponding to the Diels-Alder reaction confirm the formation of a transition state structure.
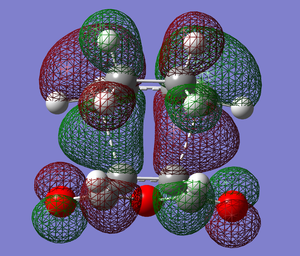 |
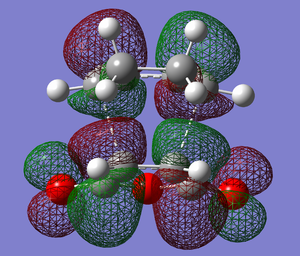 |
The HOMO above shows the overlap of the HOMO of cyclohexa-1,3-diene with the LUMO of maleic anhydride, proving the formation of a transition structure.
The secondary orbital overlap effect [6], a stabilising secondary interaction between the π-orbitals on the diene and on the C=O of maleic anhydride, predicts this too as there is no such interaction on the exo transition structure but there is on the endo. However, it can be seen in the HOMO and LUMO below that these interaction are not considered as there is no overlap between the π-orbitals. However, the π-orbitals are in phase with each other and so can potentially form a stabilising interaction.
(Talk about the sterics involved and the role they play Tam10 (talk) 17:44, 12 November 2015 (UTC))
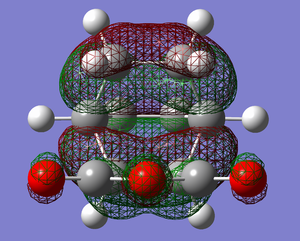 |
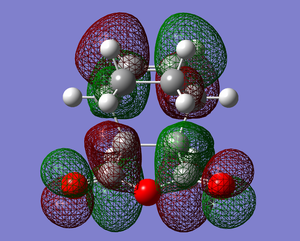 |
Above shows the HOMO and LUMO of the exo transition structure.
The bond forming lengths of both transition structures are compared in the table below.
| Bond forming lengths (Å) | ||
|---|---|---|
| HF/3-21G | B3LYP/6-31G | |
| Endo TS | 2.23070 | 2.26846 |
| Exo TS | 2.26075 | 2.29062 |
In both levels of theory, the exo bond forming lengths are longer than those in the endo, this supports the theory of the secondary orbital effect.
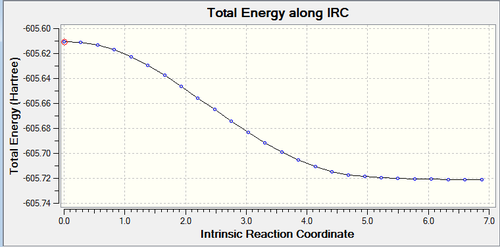
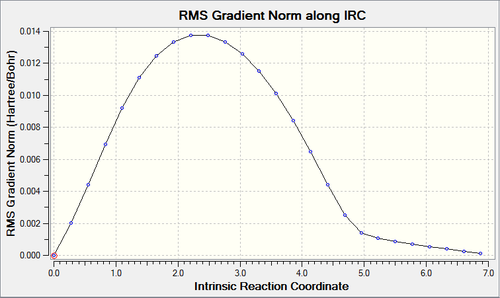
IRC calculations were run on both the transition structures in order to find the lowest energy transition structure. These can be views below and the log file for the endo can be found here and the exo here.
 |
 |
 |
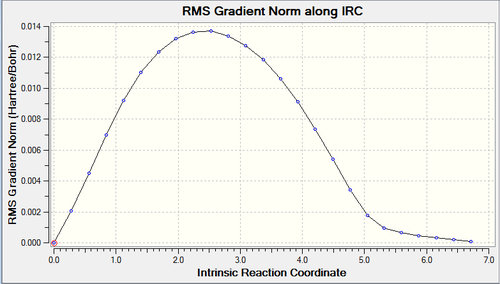 |
Above are the IRC plots for the endo (top) exo TS (below) and the RMS reaching zero shows the successful minimisation of energy.
Results Tables
| HF/3-21G | B3LYP/6-31G(d) | |||||
|---|---|---|---|---|---|---|
| Electronic energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | Electronic energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | |
| At 0 K | At 298.15 K | At 0 K | At 298.15 K | |||
| Endo TS | -605.610368 | -605.414902 | -605.405476 | -612.683397 | -612.502143 | -612.491790 |
| Exo TS | -605.603591 | -605.408139 | -605.398679 | -612.679311 | -612.498013 | -612.487663 |
| Cyclohexa-1,3-diene | -230.539671 | -230.407712 | -230.403444 | -233.415880 | -233.293224 | -233.288629 |
| Maleic anhydride | -375.103512 | -375.042910 | -375.038078 | -379.289535 | -379.233652 | -379.228469 |
The thermochemical data of the reactants and transition structures are tabulated above.
| HF/3-21G | B3LYP/6-31G(d) | |||
|---|---|---|---|---|
| At 0 K | At 298.15 K | At 0 K | At 298.15 K | |
| ΔE (Endo) | 22.41 | 25.65 | 15.52 | 15.88 |
| ΔE (Exo) | 26.66 | 26.88 | 18.11 | 18.47 |
A higher level of theory has optimised the transition structure and reactants as such that the activation barrier has been decreased. This may be due to the optimisation of the transition structures to a lower energy structure.
Conclusion
Gaussian was used to study the Cope Rearrangement and two Diels-Alder reactions in two different levels of theory. The Cope Rearrangement involved two different paths with different transition stuctures: chair and boat. The imaginary frequencies for these transition structures involved the bond forming atoms and so corresponded to the Cope Rearrangement.
Studying the Diels-Alder reactions involved visualising the orbitals involved in the reaction: the HOMO-LUMO interaction obeys the Woodward Hoffman rules and so is a thermally allowed reaction. The reaction between cyclohexa-1,3-diene was interesting in particular as the transition state oculd be of two orientations: the endo and exo. It was found that the endo transition state was more stable than the exo which was further supported by bond forming lengths.
The activation energies of these reactions were also calculated, showing that a higher level of theory brought the values to those found in literature and thus were closer to the exact structures, showing the successful generation of transition structures.
References
- ↑ S. J. Rhoads, N. R. Raulins. Organic Reactions. 1975(22): 1–252. DOI:10.1002/0471264180.or022.01
- ↑ M. B. Smith, Jerry March. March's Advanced Organic Chemistry. 2007; 1659-1673. DOI:10.1002/0470084960
- ↑ J. Clayden, N. Greeves, S. Warren. Atkins Organic Chemistry 2nd ed.. OUP Oxford; 2012. ISBN-13: 978-0199270293
- ↑ E. Lippert. The Strengths of Chemical Bonds. Butterworths Publications Ltd., London 1958. DOI:10.1002/ange.19600721618
- ↑ A. Bondi. van der Waals Volumes and Radii. J Phys Chem. 1964;68(3):441–51. DOI:10.1021/j100785a001
- ↑ M. A. Fox, R. Cardona, N. J. Kiwiet. Steric effects vs. secondary orbital overlap in Diels-Alder reactions. J Org Chem 1987;52(8):1469–74. DOI:10.1021/jo00384a016
