Rep:Mod:SDG01345038
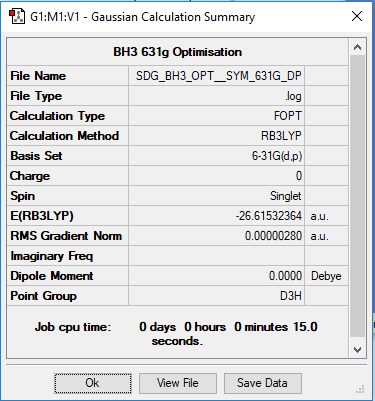
Borane BH3
B3LYP/6-31G Level
Item Value Threshold Converged?
Maximum Force 0.000006 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000022 0.001800 YES
RMS Displacement 0.000015 0.001200 YES
Frequency analysis log file SDGoptimisedsymmetrybh3.LOG
Ng611 (talk) 12:31, 5 June 2019 (BST) This is your optimisation .log file, not your frequency .log file
Low frequencies --- -2.2126 -1.0751 -0.0055 2.2359 10.2633 10.3194 Low frequencies --- 1162.9860 1213.1757 1213.1784
test molecule |
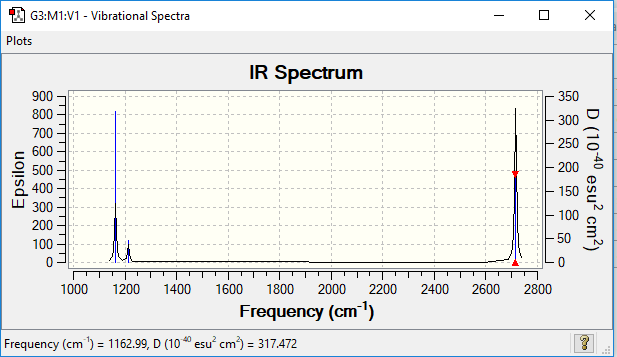
Vibrational spectrum for BH3
| wavenumber (cm-1 | Intensity (arbitrary units) | symmetry | IR active? | type |
| 1163 | 93 | A2" | yes | out-of-plane bend |
| 1213 | 14 | E' | slightly | bend |
| 1213 | 14 | E' | slightly | bend |
| 2582 | 0 | A1' | no | symmetric stretch |
| 2715 | 126 | E' | yes | asymmetric stretch |
| 2715 | 126 | E' | yes | asymmetric stretch |
Despite there being 6 vibrational modes, only 3 peaks are seen on the infrared spectrum for borane above. One of them, as seen in the previous table is IR inactive, as there is no overall dipole change, so does not show up. Next, there are two occasions where the modes have the same vibrational frequency (wavenumber). This means that they overlap on the spectrum and show up as the same peak. Therefore there are three visible peaks.
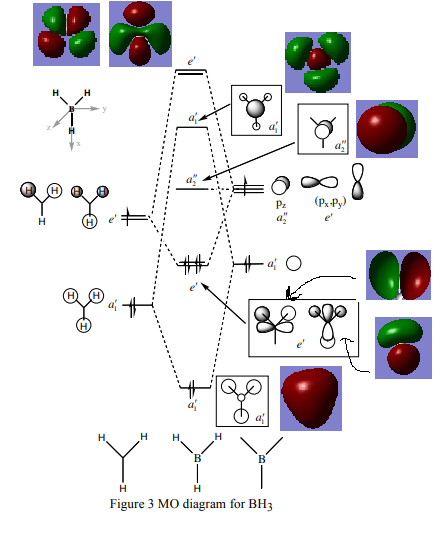
Molecular orbital diagram for borane
Above is the MO diagram for borane.[1] There is not a huge difference between the calculated molecular orbitals and the real MO's. This can be seen as their shape and relative orientations are extremely similar. If there was to be one difference it would be that the real MO's have a delocalised electron representation, where the orbitals are diffuse and not point structures. However, overall this shows that the LCAO approach is valid, accurate to an extent and useful for seeing in what order and orientation the orbitals combine to form the molecular orbitals. The LCAO approximation from quantum mechanics suggests that there is a smooth transition from the MO to the separated AO's as the bond distance tends to infinity. This can be seen as a difference between the two in the above diagram as before the AO's are combined to form the delocalised MO's, they are separate spheres that are not seen to be spatially interacting.
Determining the association energy of the N-B bond in H3NBH3
Finding the relative energies of the separated fragments
Shown above in the tables are the total energies of the separated ammonia and borane fragments and then the combined molecule. Due to differences in basis sets it is not possible to compare these directly and only relative energies can be used. The energies are reported in atomic units (A.U). It is known the accuracy of energy calculations on Gaussian are to about 5kJ/mol. This coverts to around 0.019 Hartrees, used in AU. Therefore, the energies that will be used for the relative energy calculations below are as followsː
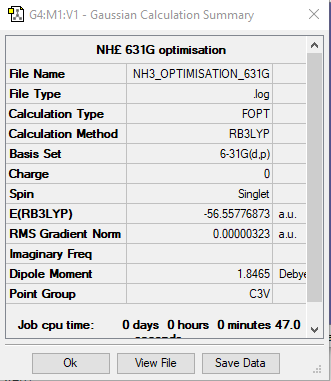
E(NH3)ː -56.56 ± 0.019 Hartrees
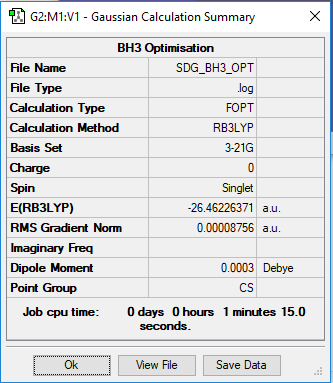
E(BH3)ː -26.46 ± 0.019 Hartrees
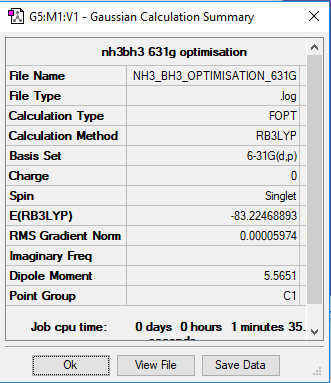
E(H3NBH3)ː -83.22 ± 0.019 Hartrees
Ng611 (talk) 12:37, 5 June 2019 (BST) Round at the END, not with your initial values. You've obtained an incorrect result because you rounded too early.
Therefore, using the formula shown below and comparing relative energies, it is possible to calculate the association energy of the N-B bond.
ΔE=E(NH3BH3)-[E(NH3)+E(BH3)]
ΔE=(-83.22)-((-56.56)+(-26.62))
ΔE= -0.04 ± 0.057 Hartrees
It was then possible to convert the above into kJ/mol, which was found to be around -105kJ/mol. This seems like a reasonable value for a bond energy especially this one as it would be a weak bond, giving me some confidence that the Gaussian calculations were taken out correctly. Comparing it to the C-C bond strength value in H3C-CH3 (ethane), which has a bond dissociation value of 368kJ/mol[2] (so association value of -368kJ/mol), this is a low value. Therefore this dative bond is a weak bond relative to others of a similar type.
Links to the log files for optimised NH3, BH3 and H3NBH3 are below. All calculations were of basis set 6-31G(d,p) and method RB3LPY.
Ng611 (talk) 12:34, 5 June 2019 (BST) Where are all the other items we asked for?
NI3 Optimisation
Below is a link to the LOG file where the results from the NI3 frequency calculation can be found. This followed an optimisation having locked the point group to C3v.
NI3FREQUENCYATTEMPT1SAMGUBBINS.LOG
Below is the summary table for the calculation that was carried out for NI3.
Below is the item table for NI3 showing the convergence and hence the success of the calculation.
Item Value Threshold Converged?
Maximum Force 0.000094 0.000450 YES
RMS Force 0.000049 0.000300 YES
Maximum Displacement 0.001088 0.001800 YES
RMS Displacement 0.000610 0.001200 YES
Below are the low frequencies for NI3.
Low frequencies --- -12.7179 -12.7118 -6.4125 -0.0040 0.0189 0.0621 Low frequencies --- 101.0754 101.0761 147.4556
Below is the Jmol for the optimised NI3.
test molecule |
The bond distance calculated on the Gaussian software was 2.184 Å.
Ionic Liquids Mini Project
Optimisation of N(CH3)4+ and P(CH3)4+
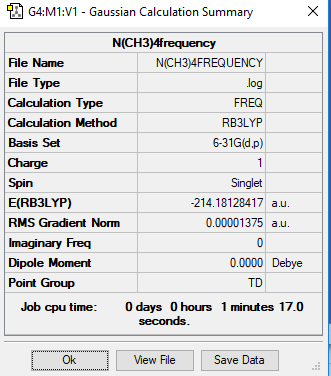
Links to the LOG files for both frequency optimisations are linked below as well as the summary tables and Jmol animations for the stated above molecules.
Below is the Jmol file for the P(CH3)4+ optimisation.
test molecule |
Below is the Jmol file for the N(CH3)4+ optimisation.
test molecule |
Below are the summary tables for the optimisations mentioned above.
Below is the item table and low frequencies table for the nitrogen centred molecule to show that the frequency optimisation was successful.
Item Value Threshold Converged? Maximum Force 0.000024 0.000450 YES RMS Force 0.000014 0.000300 YES Maximum Displacement 0.000169 0.001800 YES RMS Displacement 0.000150 0.001200 YES
Low frequencies --- -0.0007 0.0008 0.0010 22.6539 22.6539 22.6539 Low frequencies --- 188.8185 292.7544 292.7544
Again, below are the item and low frequency tables but this time for the phosphorus centred molecule.
Item Value Threshold Converged? Maximum Force 0.000027 0.000450 YES RMS Force 0.000022 0.000300 YES Maximum Displacement 0.000436 0.001800 YES RMS Displacement 0.000388 0.001200 YES
Low frequencies --- 0.0004 0.0010 0.0013 26.3157 26.3157 26.3157 Low frequencies --- 160.9744 195.4740 195.4740
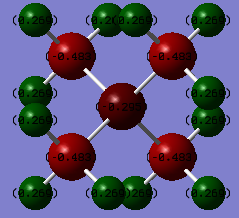
Ion Charge Distribution
Shown below is a table representing the numerical charges on each of the atoms in the tetramethylammonium ion. The overall charge can be found be summing the last column of total charge which gives the expected value of 1. All dipole units are in Deby and are only accurate to 0.01.
Atom Number of atoms Charge/Atom Total charge
Hydrogen 12 0.27 3.24
Carbon 4 -0.48 -1.92
Nitrogen 1 -0.30 -0.30
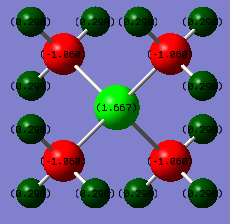
Shown below is a table representing the numerical charges on each of the atoms in the tetramethylphosphonium ion. The overall charge can be found by summing the total charge column, and again can be found to be positive 1. All dipole units are in Deby and are only accurate to 0.01.
Atom Number of atoms Charge/Atom Total charge
Hydrogen 12 0.30 3.60
Carbon 4 -1.06 -4.24
Phosphorus 1 1.67 1.67
Discussion
When being represented as [NR4]+, this does not mean that the positive charge is located on the nitrogen atom which is how it may seem on a pictorial representation.The formal charge on the nitrogen atom can be found using the equation below[3]ː
Formal Charge = (Group Number) - 1/2(Number of electrons in covalent bonds) - (Number of electrons in lone pairs)
For the tetramethylammonium ion this equates toː
Formal Charge = (5) - 1/2(8) - (0) = 1
This indicates that the positive charge in the ion is located on the nitrogen atom in the centre of the molecule. However, having used the Gaussian program to calculate the charge distribution as seen in the representations above, the positive charge is actually delocalised over the entire molecule and in fact the nitrogen itself is slightly negative, and it is the 12 hydrogen atoms bearing all of the positive charge contribution. The value for carbon is also negative, in fact the most negative in the molecule. Despite being the most electronegative atom in the molecule, nitrogen doesn't bear the largest proportion of negative charge per atom. It is actually carbon that does. This implies that the electronegativity argument is not sufficient to explain fully charge distribution in the molecule and that MO theory relieves this limit and allows the real picture to be seen. Hydrogen however does follow the electronegativity argument. It is the most electropositive atom in the molecule and hence bears the positive charge as expected.
Ng611 (talk) 12:42, 5 June 2019 (BST) You mention a dipole (which is good). Can you discuss how the partial charges and symmetry relate to the overall dipole?
For the tetramethylphosphonium ionː
Formal Charge = (5) - 1/2(8) - (0) = 1
This indicates that the positive charge on the ion is located on the phosphorous in the centre of the molecule. Despite this not being the correct way of explaining how the charge is distributed, it does turn out that the phosphorus is actually positively charged within the molecule. Phosphorous is more electropositive than carbon according to the Pauling electronegativity scale[4]. This means that according to theory it would be less able to accommodate any negative charge on the molecule relative to carbon, which turns out to be true as the four carbon atoms bear all of the negative charge in this ion, with hydrogen and nitrogen being delta positive to create the overall positive 1 charge. Again, the hydrogen's are delta positive as expected because they're the most electropositive atoms in the molecule.
To compare the two, it is easiest to compare atom by atom. For carbon, it is more delta negative in the tetramethylphosphonium ion. This is expected as it is the most electronegative atom in the molecule according to the Pauling scale and therefore is best placed to accommodate the negative charge. However, a difference from what would be expected occurs when looking at Hydrogen. Being the most electropostive atom by far in the tetramethylammonium ion, it is less relatively electropostive in the tetramethylphosphonium ion. This is because the ΔElectronegativity between the most and second most electropostive atoms in tetramethylammonium (H and C) are less than in tetramethylphosphonium (H and P). therefore it would be expected that the hydrogen's would have to accommodate more of the positive charge in tetramethylammonium than in tetramethylphosphonium, but this is not the case. Again this is down to limitations of the theory that can be improved by using MO theory.
Molecular Orbital Analysis
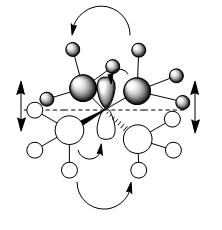
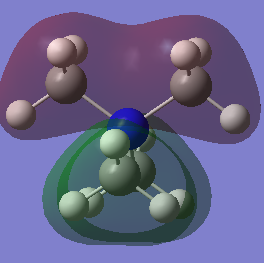
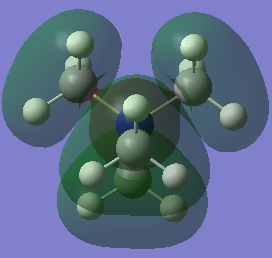
MO 7
In MO 7 there is one node located through the centre of the nitrogen atom perpendicular to the Pz orbital as seen by the dashed line on the drawn combination of FO's diagram. Overall, this is a bonding interaction as either side of the node all orbitals are in phase and strongly bonding hence lowering the overall energy of the molecule. The only antibonding interaction is when the spatially large methyl groupsof opposite phases on either side of the node interact destructively, but this effect is minimal, so still overall bonding.
Ng611 (talk) 12:43, 5 June 2019 (BST) You need to represent your CH3 orbitals with an appropriate fragment orbital (in all three orbitals). However this is a good LCAO otherwise. You also include arrows (presumably to highlight the key orbital interactions). You should consider adding descriptions to your labels though.
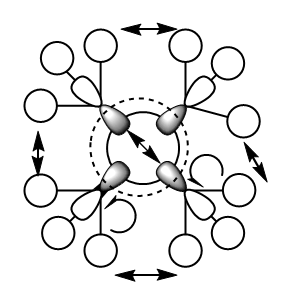
MO 10
MO 10 is interesting because of the way the node is placed. As seen in the diagram above, the node is circular, between the out of phase interactions of the 2p orbitals on carbon and the 2s orbital on the central nitrogen. All of the methyl groups are internally in phase and thus the methyl groups' spatial interactions will be in phase, bonding and hence lower the energy of the molecule overall. Despite this, the strong out of phase overlap between the 2s on nitrogen and the 2p orbitals on the four carbons means that this MO is overall antibonding and would not result in stable bonds being formed.
Ng611 (talk) A very confused orbital diagram here. The methyl FOs are actually s-type and result in an antibonding interaction with the molecule. You actually assign a p-type FO for the methyl group that gives an antibonding interaction with the central atom. I'm guessing this is to account for the 'nubs' of electron density that exist along the methyl bonds, but then you would expect to have a bonding interaction between the central atom and the methyl groups. As it happens, these nubs are not actually significant.
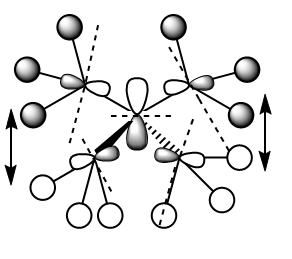
MO 12
MO 12 has 5 nodes overall and therefore it may be expected that it is antibonding, but in fact it is not. The 2p orbital on the central nitrogen is in phase with the 2p orbitals on each carbon (2 of each phase, see diagram). Each methyl's respective hydrogen atoms are also of the same phase as its 2p orbital and so this is a favourable interaction. The only unfavourable interaction again comes from the central node where either side of it the methyl groups are of different phases so spatially will not interact favourably. However, this is a small contribution and similar to what is seen in MO 7, hence overall this is a bonding MO.
Ng611 (talk) 12:56, 5 June 2019 (BST) A bit dubious of your FOs here as you seem to have a nodal plane that passes through 2 of your three methyl hydrogens, yet your FOs do not account for that.