Rep:Mod:SAS123

Ammonia

General Information

Molecule	NH3
Method	RB3LYP
Basis Set	6-31G(d,p)
Energy	-56.55776873 au
RMS Gradient	0.00000485 au
Point Group	C3v
N-H Bond Length	1.01798 Å
H-N-H Bond Angle	105.741°

Items Table

         Item               Value     Threshold  Converged?
 Maximum Force            0.000004     0.000450     YES
 RMS     Force            0.000004     0.000300     YES
 Maximum Displacement     0.000072     0.001800     YES
 RMS     Displacement     0.000035     0.001200     YES

NH3

[Optimised NH3 .log file]

Vibrations

Animating vibrations

1. How many modes do you expect from the 3N-6 rule?

I would expect 6 vibrational modes as there are 4 atoms and (3x4)-6=6.

2. Which modes are degenerate (ie have the same energy)?

Vibrational modes 2 and 3, and 5 and 6 are degenerate as they have the same energy.

3. Which modes are "bending" vibrations and which are "bond stretch" vibrations?

Vibrational modes 1,2 and 3 are bending modes and modes 4,5 and 6 are stretching modes.

4. Which mode is highly symmetric?

Vibrational mode 4 is the highly symmetric stretch.

5. One mode is known as the "umbrella" mode, which one is this?

Mode 1 is the "umbrella" mode

6. How many bands would you expect to see in an experimental spectrum of gaseous ammonia?

I would expect 4 bands in an experimental spectrum of gaseous ammonia, as there are 4 non-degenerate modes.

Atomic Charge

I would expect the charge on the N atom to be more negative than the H atom, as the N atom is more electronegative and draws electron density from its bonds and has a lone pair of electrons, making it more negatively charged. the charge on the N atom is -1.125 and the charge on the H atoms is 0.375.

Haber-Bosch Process

Nitrogen

General Information

Molecule	N2
Method	RB3LYP
Basis Set	6-31G(d,p)
Energy	-109.52412868 au
RMS Gradient	0.00000060 au
Point Group	D∞H

Items Table

         Item               Value     Threshold  Converged?
 Maximum Force            0.000001     0.000450     YES
 RMS     Force            0.000001     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000000     0.001200     YES

N2

[Optimised N2 .log file]

Hydrogen

General Information

Molecule	H2
Method	RB3LYP
Basis Set	6-31G(d,p)
Energy	-1.17853936 au
RMS Gradient	0.00000017 au
Point Group	D∞H

Items Table

         Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000450     YES
 RMS     Force            0.000000     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000001     0.001200     YES

H2

[Optimised H2 .log file]

Haber-Bosch Reaction Energy Calculation

E(NH3)= -56.55776873 au

2*E(NH3)= -113.11553746 au

E(N2)= -109.52412868 au

E(H2)= -1.17853936 au

3*E(H2)= -3.53561808 au

ΔE= -0.0557907 au = -146.48 kJ/mol

Therefore we can see that the product of ammonia is thermodynamically more stable than the reactants of hydrogen and nitrogen. This value was compared to the literature value of -92 kJ/mol, which was smaller in magnitude than the value calculated above. This literature value is an enthalpy change and in the calculation there were no specific details of the pressure or volume, as it is purely the change in energy and stability going from hydrogen and nitrogen to ammonia.

Chlorine

General Information

Molecule	Cl2
Method	RB3LYP
Basis Set	6-31G(d,p)
Energy	-920.34987886 au
RMS Gradient	0.00002510 au
Point Group	D∞H

Items Table

         Item               Value     Threshold  Converged?
 Maximum Force            0.000043     0.000450     YES
 RMS     Force            0.000043     0.000300     YES
 Maximum Displacement     0.000121     0.001800     YES
 RMS     Displacement     0.000172     0.001200     YES

Cl2

[Optimised Cl2 .log file]

Vibrations

There is only one vibrational frequency, as was expected as Chlorine is a linear molecule and so the expression 3N-5 is used. As chlorine has 2 atoms, the number of frequencies is (3x2)-5=1. This is a low vibrational frequency as the chlorine atoms are large and heavy, giving a large reduced mass and therefore short wavenumber and frequency. However, as chlorine is a diatomic molecule, the vibrational mode is IR inactive as there is no change in dipole moment. As there would be no IR spectrum formed by Chlorine, there was no literature IR spectrum to compare to, as the only vibrational mode was IR inactive.

Charge

As chlorine is a diatomic molecule, the bond is not polar and so there is no net charge on either atom.

Molecular Orbitals

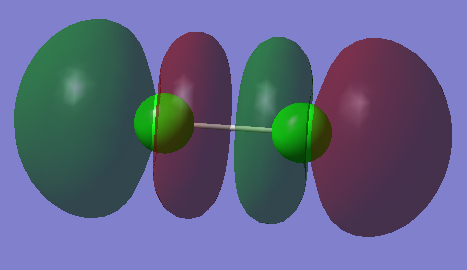
This orbital is the LUMO of the molecule, it is a σ* orbital and has a symmetry label of ungerade. It has an energy of -0.14206 au and is created by the interaction of the 3p_z AOs out of phase from the chlorine atoms. It is unoccupied and is an antibonding orbital.

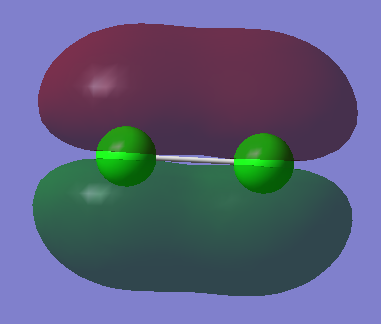
This orbital is the HOMO of the molecule, it is a π* orbital and has a symmetry label of gerade. It has an energy of -0.31361 au and is created by the interaction of the 3p_x AOs out of phase from the chlorine atoms. It is occupied and is an antibonding orbital.

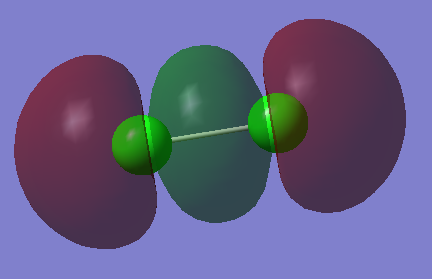
This orbital is in the HOMO/LUMO region, it is a π orbital and has a symmetry label of ungerade. It has an energy of -0.40695 au and is created by the interaction of the 3p_x AOs in phase from the chlorine atoms. It is occupied and is a bonding orbital.

This orbital is in the HOMO/LUMO region, it is a σ orbital and has a symmetry label of gerade. It has an energy of -0.47392 au and is created by the interaction of the 3p_z AOs in phase from the chlorine atoms. It is occupied and is a bonding orbital.

This orbital is slightly deeper in energy than the HOMO/LUMO region, as chlorine is an electronegative element, the MO is much deeper in energy. It is a σ* orbital and has a symmetry label of ungerade. It has an energy of -0.77746 au and is created by the interaction of the 3s AOs out of phase from the chlorine atoms. It is occupied and is an antibonding orbital.

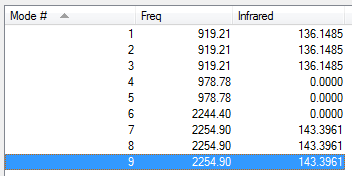
Silane Vibrations

We can see that there are 3N-6 vibrational modes as the molecule is non-linear, so in this case, there should be (3x5)-6= 9 vibrational modes. However some modes are degenerate and so there are only 4 different non-degenerate vibrational modes.

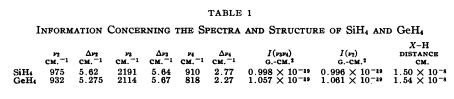
Below is a literature table of vibrations of silane.

However we can see from this, that because the two non-degenerate modes at around 2250 cm^-1 overlap and so only one peak is observed in the spectrum, as demonstrated in the table.