Rep:Mod:SAITYM945

Year 3 Physical Computational

Cope Rearrangement

Introduction

Cope Rearrangement is a [3,3]-sigmatropic rearrangement of 1,5-dienes. Cope rearrangement of 1,5-hexadiene had been subject to many computational studies and it is now generally accepted that the [3,3]-sigmatropic shift mechanism occurs via a 'boat' or a 'chair' transition. The objective of this tutorial course is to work out the low energy minima and the transition structure on the C₆H₁₀ potential energy surface to determine the preferred reaction mechanism. All conformers are labeled as the following from Appendix 1

Cope Rearrangement

Optimizing the Reactants and Products

1,5-hexadiene (anti)

In the first part of this exercise, the 1,5-hexadiene with an 'anti-linkage'(the 4 center carbon atoms are of app conformation)was drawn on Gaussian, and optimized using the HF/3-21G level of theory.

'anti 1' 1,5-hexadiene

The optimized 'anti' 1,5-hexadiene had total energy of -231.69260235 Hartrees with point group of C2 (anti 1).

1,5-hexadiene (gauche)

A 1,5-hexadiene molecule with 'gauche-linkage' was drawn and similarly to the example above was optimized using the HF/3-21G level of theory. The optimized 'gauche' 1,5-hexadiene molecule (gauche 4) had electronic energy of -231.69153035 Hartrees and a point group of C2 .

'gauche 4' 1,5-hexadiene

I had predicted that the gauche conformer is higher in energy than the anti conformer and this is due to higher stabilization energies in 'anti' form than the 'gauche' form. The anti form have 4 σ_C-H/σ*_C-H and 2σ_C-C/σ*_C-C interactions which have higher stabilizing energies than the 2 σ_C-H/σ*_C-H , 2 σ_C-C/σ*_C-H and 2 σ_C-H/σ*_C-C interactions present in the gauche form. The anti form also avoids the increased steric repulsion from the carbon atoms in the gauche conformation which also lower the energy of the anti conformer relatively. This prediction agrees with the energy results when you compare the total energies between 'anti 1' and 'gauche 4' where 'anti 1' conformer has lower energy. However out of the 10 conformers with distinct energy levels, when optimized using the HF/3-21G level of theory, gauche 3 is the lowest energy conformer. A possible explanation could be due to favorable orbital interaction between two π orbitals on the terminal carbons overcompensating for the steric repulsion and lower stablisation energies in gauche 3 conformer allowing it to lie in a lower energy level than the anti conformers.

'gauche 3' 1,5-hexadiene

Gauche 2 had electronic energy level of -231.69166701 Hartrees with a point group of C2.

Optimization of C_i anti 2 conformer of 1,5-hexadiene

The 'anti 2' conformer which is the lowest energy 'anti' conformer was drawn and optimized at the HF/3-21G level of theory giving electronic energies of -231.69253528 Hartrees and point group of C_i. The HF/3-21G optimized 'anti 2' 1,5-hexadiene was then re-optimized at the B3LYP/6-31G* level giving electronic energy at -234.61170280 Hartrees. The structures of both anti 2 conformer optimized at HF/3-21G and B3LYP/6-31G* were compared and the energies as well as the dihedral angles were seen to be significantly different. The conformer optimized at the HF/3-21G level had dihedral angles of 114.66879^o where as the conformer optimized at the B3LYP/6-31G* level had a dihedral angle of 118.52813^o. This change in dihedral angle is followed by a lowering of energy in the molecule. This could be a consequence of the dihedral angle, when re-optimized, moving closer to 120^owhich is the favored dihedral angle for atoms on the carbon adjacent to the carbon with the double bond. This 120⁰angle allows two σ bonds to interact with the π system rather than one at 90^o as well as eclipsing one of the hydrogen atom to the cis hydrogen atoms where the interaction between those hydrogen atoms is slightly van der waals attractive further lowering the energy. This favored conformation is called the A^1,3 eclipsed conformation and explains the shift of the dihedral angle going closer to 120^o when re-optimized..

Frequency calculation were done on the re-optimized 'anti 2' 1,5-hexadiene and the calculated energy level were noted down in Table 1.

HF/3-21G optimized 'anti 2'1,5-hexadiene

B3LYP/6-31G* optimized 'anti 2'1,5-hexadiene

Different Calculated energies for 'anti 2' 1,5-hexadiene(Table 1)

Different energies with correction	Energy/Hatrees
Sum of electronic and zero-point Energies	-234.469212
Sum of electronic and thermal Energies	-234.461856
Sum of electronic and thermal Enthalpies	-234.460912
Sum of electronic and thermal Free Energies	-234.500821

Optimizing the Boat and Chair transition state

Optimizing the Chair transition

An allyl fragment (CH₂CHCH₂)was drawn and subsequently optimized at the HF/3-21G level. This optimized fragment was then copied and pasted, and orientated in such a way that it formed a 'guess' transition structure for the chair transition. The terminal carbons were modeled in the guess transition so that it was roughly 2.2A apart. This transition state was then optimized using two different methods, one method by computing the force constant at the beginning of the calculation and the other by using the redundant coordinate editor.

Computing the force constant and optimizing to a TS(Berny)

Using the HF/3-21G level of theory, the guess transition state was optimized to a TS(Berny) with Force constant calculated once. The optimized structure had only one imaginary vibration at -817.9cm^-1,bond length between terminal carbons at 2.02 and electronic energy at -231.61932245 Hartrees

Vibration of the imaginary frequency for the chair transition(CLICK)

optimized chair transition

Optimizing the transition using a redundant coordinate editor

The bond length or the distance between the two terminal carbons opposite to each other in the guess transition was frozen and fixed using the redundant coordinate editor. The guess transition was then optimized to a minimum at the HF/3-21G level initially. When the optimization completed, the bonds were then relaxed again using the redundant coordinate editor and optimized this time to a TS(Berny) without calculating the force constant. The optimized chair transition gave only one imaginary frequency at -817.85^-1, bond length between terminal carbons at 2.02 and electronic energy at -231.61932243 Hartrees

Optimizing the Boat transition using the QST2 method

The QST2 method was used to optimize the boat transition at the HF/3-21G level. This method requires you to input the reactants and the products, and automatically calculates the transition state. It is important to number the atoms of the reactants and the product accordingly and the transition state structure cannot be too far away from the structure of the reactants and the product or the method will not work. This was outlined when trying to optimize the boat transition using 'anti 2' 1,5-hexadiene modeled as the reactant and the product where it failed to rotate around the center bond and processed the wrong transition state. It is however still possible to optimize the boat transition starting from 'anti 2' by manually modelling closer to the gauche form and processing it under the QST2 method. The QST2 method successfully optimized the boat transition giving an imaginary frequency at -839.87cm^-1, bond length at 2.14A and electronic energy at -231.60280240 Hartrees.

reactant

product

boat transition

incorrect transition calculated from QST2 method

Vibration of the imaginary frequency for the boat transition(CLICK)

Using the Intrinsic Reaction Coordinate method (IRC)

The IRC method allows you to follow the lowest energy path from the transition to the local minimum on a potential energy surface. The IRC method was applied to the chair transition and it can be seen that the chair transition connects to form the gauche 2 conformer.

IRC of chair transition

Gauche 2

Re-optimization of transition states using the B3LYP/6-31G* level

The chair and boat transitions were re-optimized in the B3LYP/6-31G* level. Both transitions lowered its energy significantly. The chair transition gave electronic energy of -234.55698303 Hartrees, bond length of 1.96A and imaginary frequency at -565.54cm^-1. The boat transition gave electronic energy of -234.54309308 Hartrees, bond length of 2.20Å and imaginary frequency at -530.46cm^-1. Table 2 shows the energies of the transitions optimized at the HF/3-21G and B3LYP/6-31G* level. Gauche 3 is the lowest energy conformer relatively and was therefore used as the reactants for these transitions to work out the activation energies subsequently. Activation energies are in kcal/mol where 1 hartree = 627.509 kcal/mol.

Comparison of Energies/hartree (Table 2)

	HF/3-21G			B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
Chair TS	-231.619322	-231.466698	-231.461340	-234.556983	-234.414929	-234.409009
Boat TS	-231.602802	-231.450929	-231.445300	-234.543093	-234.402341	-234.396006
gauche 3 (Reactant)	-231.692661	-231.539486	-231.532646	-234.611329	-234.468693	-234.461464

Activation energies of the transition states in kcal/mol (Table 3)

	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Experimental
	0K	298.5K	0K	298.5K	0K
ΔE of Chair TS	45.675125	44.745156	33.737393	32.915984	33.5 ± 0.5
ΔE of Boat TS	55.570314	54.810401	41.636477	41.075484	44.7 ± 2.0

The activation energies are generally in good agreement to experimental values suggesting computational method are a good method in estimating activation energies of reactions.

B3LYP/6-31G* optimized chair transition state

Vibration at the imaginary frequency for B3LYP/6-31G* optimized chair transition state (CLICK)

B3LYP/6-31G* optimized boat transition state

Vibration at the imaginary frequency for B3LYP/6-31G* optimized boat transition state (CLICK)

As it can be seen in the table and the models, when re-optimized at the B3LYP/6-31G* level, although the geometry of the transition states do not change too much, the energy difference are very large. The differences between the HF/3-21G and B3LYP/6-31G* optimized structures are around 2.9 hartree which is around 1820kcal/mol. This is a massive energy difference and empathizes the importance of optimizing from lower level to higher, in this case HF/3-21G to B3LYP/6-31G* level of theory.

The Diels Alder Cycloaddition

Cycloaddition of Ethylene and Butadiene

Both ethene and cis-butadiene were optimized using the AM1 semi-empirical molecular orbital method, and then at the HF/3-21G and B3LYP/6-31G* level of theory. The energies are given in Table 5 where combined energies will be used to work out the activation energies of the transition state. The HOMO and the LUMO of cis-butadiene are anti-symmetric and symmetric respectively and the HOMO and the LUMO of ethene are symmetric and anti-symmetric respectively.

Energies of ethene and cis-butadiene at AM1 semi-empirical and B3LYP/6-31G* level (Hartree) (Table 5)

	AM1 semi-empirical			B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
cis-butadiene	0.048797	0.134552	0.138573	-155.985949	-155.900825	-155.896783
ethene	0.026190	0.077198	0.080252	-78.587458	-78.536231	-78.533189
Combined energies	0.074987	0.21175	0.218825	-234.573407	-234.437056	-234.429972

HOMO and LUMO of cis-butadiene and ethene

HOMO(a)	LUMO(s)	HOMO (s)	LUMO (a)

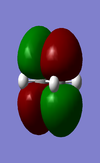Ethylene+cis butadiene transition structure

The transition structure was characterized and optimized using the QST2 method. Cyclohexene was optimized at the AM1 semi-empirical molecular orbital method, and then at the HF/3-21G and B3LYP/6-31G* level of theory to be inputted as the product for the QST2 method, with ethene and cis-butadiene as the reactants. The QST2 method gave a Ethylene+ cis butadiene transition structure, where when IRC was run on it, connected to give the cyclohexene, confirming that it is in fact the wanted Diels-Alder transition state. The transition state was re-optimized at the B3LYP/6-31G* level.

reactants	product	transtion state	IRC	Vibration at imaginary freqeuncy

HOMO of transition state (a)	LUMO of transition state (s)	lowest positive frequency vibrations

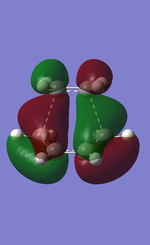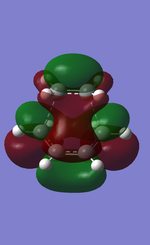The molecular orbitals of the transition state is plotted above with HOMO anti-symmetric and LUMO symmetric with respect to the plane. The bond length of the partially formed C-C bond was 2.27Å. Typical sp3 and sp2 carbon carbon bond length are 1.54Å and 1.35Å respectively. The van der Waals radius of the C atom is 1.70Å. The partial bond length of 2.27Å is much bigger than the typical C-C bond lengths and therefore is a very weak bond. However it is smaller than the sum of the Van der Waals radius for carbon and therefore there must be an attractive force between the carbons. This partial bond can therefore be concluded as a result of Van der Waals attractive force between the carbon atoms.

The transition state gave a imaginary frequency of -524.78cm^-1 and looking at the vibration in the model, it can be clearly seen that the two bond formed are formed synchronously. The lowest positive frequency vibration at 135.76cm^-1 which can be seen above, is an asynchronous movement along the horizontal plane between the molecules.

The calculated HOMO of the transition is anti-symmetric MO and is an interaction between the LUMO of ethene and the HOMO of the cis-butadiene and is a bonding MO between the carbons of ethene and cis-butadiene. This reaction is allowed due to the correct orientation of the MO allowing good overlap when the two molecules approach.

Summary of energies

	AM1 semi-imperical			B3LYP/6-31G*
	electronic energies	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	electronic energies	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
transition state	0.11165469	0.253276	0.259454	-234.54389648	-234.403321	-234.396903
activation energies(kcal/mol)		26.06	25.50		21.17	20.75
Experimental activation energies(kcal/mol)	25.1 (0K)	32.8-34.3(800K)

The activation energy of AM1 semi-empirical level is generally in good agreement with experimental values. This suggest that computational methods in predicting energies of diels alder reaction at the AM1 semi-empirical level is a valid method

Diels-Alder reaction between Cyclohexa-1,3-diene and maleic anhydride

Both the endo- and the exo- transition structure were characterized and optimized using the QST2 method at the AM1 semi-empirical level and then at HF/3-21G and B3LYP/6-31G* level. Exo form gave partial bond length at 2.29Å and imaginary frequency at -448.55cm^-1. The endo form gave partial bond length at 2.268Å and imaginary frequency at -447.04cm^-1 . The energies of the transitons are listed in a table below. There is a notable difference in the partial bond length in the endo and the exo form with endo being slightly shorter. This suggest that the partial bond length is stronger in the endo transition and is more likely to be favored.

endo-	HOMO of endo	imaginary frequency vibration	exo-	HOMO of exo	imaginary frequency vibration

Summary of energies

	AM1 semi-imperical			B3LYP/6-31G*
	electronic energies	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	electronic energies	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
endo	-0.05150479	0.133494	0.143684	-612.68339669	-612.502141	-612.491787
exo	-0.05041967	0.134883	0.144882	-612.67931093	-612.498012	-612.487661

relative energies

heading	relative electronic energies (kcal/mol)
	AM1	B3LYP/6-31G*
endo	0	0
exo	0.680	2.59

secondary orbital overlap

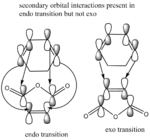
Table above shows that the endo transition is lower in energy than the exo transition with agreement at two level of theory. Endo product predominates due to it being the kinetic product with lower energy transition state. This is due to the secondary orbital overlap illustrated in a diagram on the right. The HOMO of both transitions consist of interactions between the LUMO of the malaeic anhydride and HOMO of the 1,3-cyclohexadiene which are both anti-symmetrric with respect to plane and therefore can overlap and react. However in the endo transition state, there is an extra orbital interaction that is not present in the exo transition thus leading to lower endo transitions energies. This reaction therefore is under kinetic control.Although secondary orbital overlap is likely to be the predominate force for endo being favored, another factor maybe that the exo transition state is stericly more hindered the endo transition state. This is due to the closer positioning of the sp3 hydrogen atom to the C=O carbon atom present in exo-TS but not endo-TS. The distance between these atoms is 2.53Å which is smaller than the combined van der waals radius of hydrogen and carbon atoms and therefore repulsive.