Rep:Mod:SA4213TS

Introduction

In this computational experiment, transition structures for two reactions – the Cope Rearrangement and two Diels Alder cycloadditions – were studied. This computational approach is necessary as transition structures cannot be isolated and studied experimentally. For this Gaussian 09W (Visualised via GaussView 5.0.9) was used to follow the potential energy surfaces for three reactions:

1. Cope Rearrangement of 1,5-hexadiene
2. Diels-Alder cycloaddition of ethene and s-cis-butadiene
3. Diels-Alder cycloaddition of cyclohexa-1,3-diene and maleic anhydride
• Exo
• Endo

It is necessary to understand the nature of transition states as it provides information relevant for kinetics – we can find activation energies and thus the rate of reactions - and also for reaction mechanisms in order to plan successful experiments in the laboratory.

In the Cope Rearrangement the conformation between ‘chair’ and ‘boat’ was explored to find the lowest energy, and therefore most likely conformation in the transition structure. Also studied were the differences in 1,5-hexadiene’s conformation with anti-periplanar and synclinal linkages. The difference between transition states for endo- and exo-cycloaddition products for the Diels-Alder reaction were also studied.

We used three calculation methods at differing levels of theory: Hartree-Fock/321-G, B3LYP/6-31G(d), DFT/Semi-Emperical/AM1.

With the Hartree-Fock method, the single electron wavefunctions in the system are approximated to be a single Slater determinant to produce a solution of more accurate orbitals. This is iteratively repeated until an energy minimum is achieved. This method overlooks electronic correlation instead using a mean field for electron-electron repulsion. In Density Functional Theory (DFT) instead of wavefunctions being analysed the properties are determined via studying the functional of the electron density, again using the variational principle to minimise the energy. Our procedure involved guessing a reasonable transition structure and optimising to a minimum, before optimising the transition structure using the TS (Berny) method or the QST2 method where atoms in both the optimised product and reactant are labelled and then a maxima is found on the potential energy surface linking both structures.

Nf710 (talk) 21:44, 17 January 2016 (UTC) Good brief overview of the various computational methods, you have shown some understanding

The Cope Rearrangement of 1,5-Hexadiene

Optimization of 1,5-Hexadiene conformers

In order to optimise the 1,5-hexadiene conformers optimisations to a minimum were carried out by Gaussian 09W with a 3-21G basis set using the HF method.

Conformer	Molecule	Summary	Point Group	Energy/Hartrees	Energy Difference/ kcal mol-1
Anti1			C2	-231.692602	0.03702
Anti2			Ci	-231.682793	6.19226
Gauche4			C2	-231.691530	0.70971
Gauche3			C1	-231.692661	0.00000

(You must include jmol script to display the optimised geometry for each of your files. At the moment you're showing the input geometry Tam10 (talk) 14:52, 10 January 2016 (UTC))

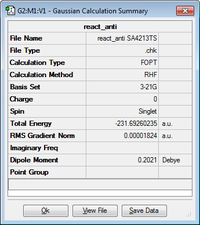
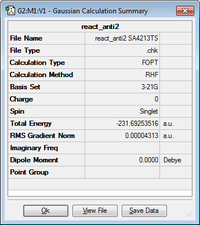
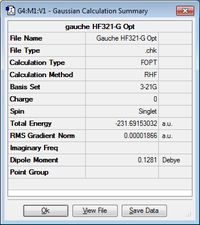
The log files can be found here: anti1, anti2, gauche4, gauche3

The 'Gauche3' conformation has the lowest energy of all the conformations of 1,5-hexadiene. This is due to the secondary orbital interactions between the two pi-bonds, we can see this when we visualise the MO, and see that the twist in the structure allows the pi-bonds to be in phase and interact with each other to reach a lower energy.

Nf710 (talk) 21:47, 17 January 2016 (UTC)Good use of the secondary orbital overlap, clearly shown

Reoptimization of 1,5-Hexadiene conformers

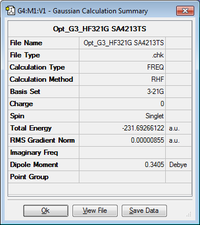
The 'anti2' conformer was reoptimised at DFT B3LYP/6-31G(d).

Conformer	Molecule	Summary	Point Group	Energy/Hartrees
Anti2		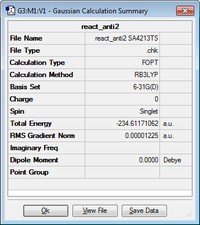	Ci	-234.611711

Whilst we have achieved a lower energy with this higher level of theory, we cannot directly compare the energies of two different methods as they are using different approximations and therefore having a different zero point and so the scaling cannot be compared. As discussed above, DFT - as a higher level of theory - produces more accurate results than HF. Density functional theory has an additional term in its hamiltonian operator to account for the exchange-correlation potential due to spin and charge. Hartree Fock does not take this into account and so we consistently get higher energies than DFT. What we can compare however, is the geometries of the optimised 'anti2' structures for DFT/6-31G(d) and HF/3-21G:

Nf710 (talk) 21:49, 17 January 2016 (UTC) Very Good understanding!

Atoms	HF/3-21G / Å	B3YLP/6-31G(d)/ Å
C1-C2	1.31618	1.33350
C2-C3	1.50882	1.50420
C3-C4	1.55317	1.54816

The carbon atoms are labelled as per the image of molecule above. The DFT/B3LYP/6-31G(d) method obtains bond lengths which are closer to literature values compared to HF/3-21G. There is a lengthening of the double bond (C1-C2) and shortening of the single bonds (C2-C3 and C3-C4) in the molecule. This increase may not be as important in a small molecule like 1,5-hexadiene, but higher level methods would be necessary to ensure reliable replication and optimisation of molecules.

Atoms	HF/3-21G / Å	B3YLP/6-31G(d)/ Å
C1-C2-C3-C4	114.62606	118.59945
C2-C3-C4-C5	180.00000	180.00000
C3-C4-C5-C6	-114.62606	-118.59945

The DFT method shows an increase in the dihedral angle of around 4° compared to the HF method.

Frequency Analysis

Next, a frequency analysis was performed on the optimised 'anti2' 1,5-hexadiene using the B3LYP/6-31G(d) method.

Energy Summary	Predicted IR Spectrum

The energy summary shows that there are no imaginary frequencies. The second derivative of energy is the force constant for the degree of freedom being studied. For an energy maxima, the second derivative will be less than zero, therefore the force constant will be negative. The IR frequencies are calculated from:

$f=\frac{1}{2\pi }\sqrt{\frac{k}{m}}$

as the second derivative of energy is the force constant, a negative value will produce an frequency with an imaginary component.

Additionally our calculation provided thermochemistry properties:

Data	Calculation at 298 K/ Hartrees
Sum of Electronic and Zero-Point Energies	-234.469218
Sum of Electronic and Thermal Energies	-234.461868
Sum of Electronic and Thermal Enthalpies	-234.460924
Sum of Electronic and Thermal Free Energies	-234.500809

These four energies show the potential energy at 0K and the zero-point energy; the second shows the energy which includes the translational, rotational, and vibrational energy modes at 298.15 K and 1 atm (E = E + E_vib + E_rot + E_trans); the third provides a correction for RT; and the last includes the entropic contribution to the energy.

Nf710 (talk) 21:59, 17 January 2016 (UTC) Nice explanation of the imaginary frequency. you should have included bond angles in geom comparison.

Optimisation of Chair and Boat Transition Structures

Next it is necessary to find the transition structures for the Cope Rearrangement. Three different methods are used (all using the HF/3-21G basis set): Optimising the chair transition state using TSBerny, optimising the chair transition state by freezing co-ordinates, and optimising the boat structure to find its transition state using the QST2 method.

Optimising the allyl fragment

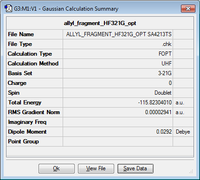
First we optimised an allyl fragment to a minimum in a similar fashion as described above.
The LOG file can be found here.

Molecule	Summary	Point Group	Energy/Hartrees
		C2v	-115.823040

Optimising the "Chair" Transition Structure

Using the HF/3-21G level of theory

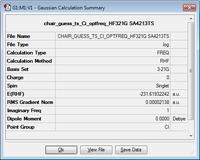
Now we have an optimised allyl fragment, we can use two of them positioned in a chair-like fashion which were then optimised using Gaussian. This was performed running and optimisation and frequency calculation, optimising to TSBerny, force constants calculated once, and an additional 'opt=noeigen' term added to keywords to prevent the calculation from crashing if we have multiplie imaginary frequencies.

Molecule	Summary	Predicted IR Spectrum	Energy/Hartrees
			-231.619322

The LOG file can be found here.

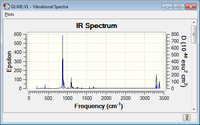
The energy summary shows one imaginary frequency was obtained, this had a value of -817.96 cm^-1. This imaginary frequency confirms that we have obtained a transition state, and its vibration is shown below.

If .gifs don't play open in a new tab to show vibrations

Using the Frozen Coordinate Method

This method uses the redundant co-ordinate editor. Using the input file for the TS Berny calculation containing the staggered optimized allyl fragments, where the co-ordinates of the terminal ends of the fragments are frozen at 2.20Å. A calculation is then run to optimize the molecule to a minimum, once again, at the HF/3-21G level keeping the rest of the molecule frozen. Next the bond breaking/bond making distances are optimised to find the transition state.

Molecule	Summary	Energy/Hartrees
		-231.619322

The LOG file can be found here.

Again the energy summary shows one imaginary frequency which had a value of -817.89cm^-1, confirming that we have obtained a transition state using this method.

Method Comparison

Both TSBerny and using the redundant co-ordinate editor (RCE) produced a transition state, which was confirmed by the negative frequency of very similar magnitude: -817.96cm^-1 for TSBerny and -817.89cm^-1 for RCE. The similarity of the frequencies and the energies (equal up to 6 decimal places) suggest both methods work well in finding the transition state for the Cope Rearrangement through a chair structure. Additionally we can look at the geometries:

Atoms	TSBerny/Å	RCE/Å
C1-C6	2.02023	2.02023
C3-C4	2.02073	2.02076

These values corroborate with each other to give us confidence in suggesting that both methods work well in producing a chair transition structure despite their differences in approach (and approximations).

Optimising the "Boat" Transition Structure

Using the QST2 method

Now we move to the boat structure and use the QST2 method at HF/3-21G level. In this method, we provide Gaussian with a guess structure for the reactant and product, and Gaussian interpolates between the two structures, reaching an energy maxima between the two arrangements of atoms to reach a transition state. With the QST2 method, as it is automated, it is necessary to provide Gaussian with our best guess of the reactant molecule before the transition state. Therefore we rotated our previously optimised 'anti2' conformer to look similar to a boat structure as shown below - for both the reactant and product C2-C3-C4-C5 atoms dihedral angles were set to 0° and C2-C3-C4 and C3-C4-C5 were set at 100°. This structure is then copied into another window in the input file to produce our reactant, with labelling such that the rearrangement has occured. With the QST2 method, we need to provide Gaussian with information linking the specific atom in the reactant molecule to where we want it to be after in the product molecule. This was done by labelling each atom in both structures. As you can see a bond has broken between C3 and C4 and formed between C1 and C6. The calculation was set to Opt+Freq optimising to QST2 with HF/3-21G.

Reactant	Product

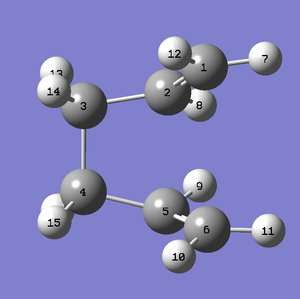
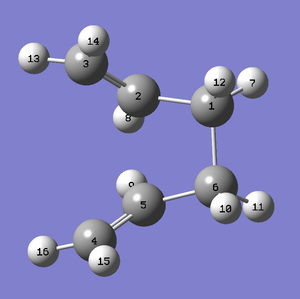
Molecule	Summary	Energy/Hartrees
		-231.60280

The LOG file can be found here.

The energy summary shows one imaginary frequency produced confirming it as a transition state. This frequency was -839.98 cm^-1. This frequency is visualised below, corresponding to the vibration that leads to the Cope Rearrangement.

Nf710 (talk) 22:02, 17 January 2016 (UTC) All your energies and frequencies are correct here

Intrinsic Reaction Coordinate (IRC) analysis

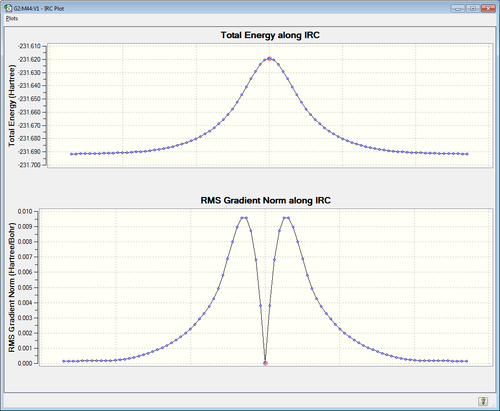
Intrinsic Reaction Coordinate analysis was then performed on the chair transition structure. This computation finds the reaction path from the transition structure, as the transition structure is the local maximum Gaussian can then calculate the steepest descent on either side of the maximum until it reaches a local minimum. It does this by running a set of optimisations until it finds the minima. Here this number of optimisations was set at 80 and Gaussian was told to follow IRC in both directions and force constants were always calculated.

IRC Analysis	Reaction Pathway

The LOG file can be found here.

The reaction pathway was calculated in both directions. As shown above the transition state is at a maximum and our reactants and products are achieved as you fall off this peak. The RMS Gradient Norm Along IRC shows the reaction going from a reactant (The RMS Gradient starting from a point tending towards zero) to a point of energy inflexion (its maximum) at which point is rapidly descends to zero again as we reach the transition state peak. Then the reverse happens as we go to the product, showing that our reaction co-ordinate was symmetric and therefore we needn't have calculated in both directions.

Nf710 (talk) 22:09, 17 January 2016 (UTC) It still looks nice though. You could have worked out the conformer it connects by optimizing down the last point on the IRC

Activation Energies

In order to find more accurate energies of our transition states, they were reoptimised at B3LYP/6-31G(d) starting from our lower level of theory HF/3-21G calculations. The energies in the table below are all in Hartrees. We can calculate the activation energies by taking the difference with the optimised 'anti2' conformation energy. The 6-31G(d) LOG file is provided for boat and chair.

	HF/3-21G			B3LYP/6-31G(d)
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.619323	-231.466697	-231.461339	-234.556931	-234.414902	-234.408975
Boat TS	-231.602802	-231.450929	-231.445300	-234.543079	-234.402348	-234.396006
Reactant (anti2)	-231.692540	-231.539539	-231.532566	-234.611711	-234.469219	-234.461869

The activation energies are provided below in kcal/mol:

	HF/3-21G	HF/3-21G	B3LYP/6-31G(d)	B3LYP/6-31G(d)	Expt.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)	45.70901	44.69558	34.08440	33.19146	33.5 ± 0.5
ΔE (Boat)	55.60357	54.76020	41.96215	41.32963	44.7 ± 2.0

From these two tables we can see that the chair transition structure has a lower energy, therefore a smaller activation energy. This tells us this is the preferred structure. Also the energies outputted by the 3-21G calculation aren't on parity with those from 6-31G(d). The activation energies are consistently higher for the Hartree-Fock method and do not match with those from experiment as well as the 6-31G(d) does.

Additionally the geometries of the two calculations can be directly compared:

Chair	Boat

BOAT	Bond Length for 6-31G(d)/Å	Bond Length for 3-21G/Å
C1-C2	1.39334	1.38144
C1-C6	2.20487	2.14004

CHAIR	Bond Length for 6-31G(d)/Å	Bond Length for 3-21G/Å
C1-C2	1.40765	1.38928
C1-C6	1.96603	2.02023

We can see that the smaller basis sets can achieve approximately similar geometry compared to the higher level 6-31G(d) calculations with bond lengths close to the higher level. However when looking at their energies, they do not reach as accurate of a value as the higher basis set calculations.

Nf710 (talk) 22:15, 17 January 2016 (UTC) Well done your energies are correct and you have come to the correct conclusion that geoms can be well approximated at a lower level of theory. you have done what is asked of you and shown a good level of understanding.

Diels Alder Cycloadditions

Like the Cope Rearrangement, Diels Alder cycloadditions are also concerted pericyclic reactions between a diene and a dienophile. Therefore they are subject to the Woodward Hoffmann rules which state that in a thermal pericyclic reaction (such as ours) the total number of (4q + 2)_s and (4r)_a components must be odd - where q and r are any positive integer and the subscripts s and a refer to the descriptions of topology for suprafacial and antarafacial interactions between the frontier orbitals. These rules forbid interactions where the orbitals have different symmetry properties, so no overlap density is possible. If allowed by the Woodward Hoffman rules the π orbitals of the dieneophile form σ bonds with the π orbitals of the diene, hence a cycloaddition. For the Diels Alder cycloadditions, preferably we would require that the diene is electron rich and the dienophile is electron poor so that there is a favourable orbital interaction between the LUMO and HOMO of the reactants. This can be achieved through substituents on our reactants. Additionally these substituents can affect regiochemistry, stabilising bonds being made through π orbital interaction - this is known as a secondary orbital effect.

Under study are two reactions, the first between 1,3-butadiene and ethene and the second between maleic anhydride and 1,3-cyclohexadiene. The reactions will be computed via the AM1 semi-empirical molecular orbital method, instead of a method such as Hartree-Fock as it is less computationally heavy as it uses NDDO (neglect of differential diatomic overlap) which replaces the Hartree-Fock secular equation by overlooking the overlap integral. Additionally AM1 makes use of experimental data to forego calculations HF would do. All of these reduce computing time when analysing more complex organic molecules.

(Good intro. Regioselectivity is also controlled through sterics Tam10 (talk) 15:00, 10 January 2016 (UTC))

Butadiene and Ethene

Separately butadiene and ethene were optimised to a minimum using semi-empirical AM1

Butadiene

Molecule	Summary	Point Group	Energy/Hartrees
		C2v	0.048797

The LOG file can be found here.

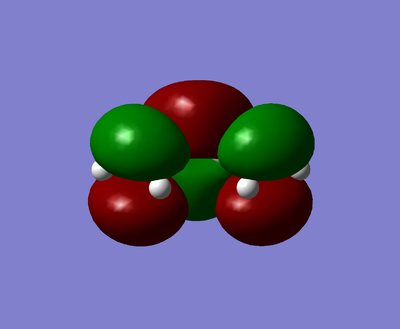
HOMO	LUMO

The visualised butadiene's MOs show that the HOMO is antisymmetric and the LUMO is symmetric.

Ethene

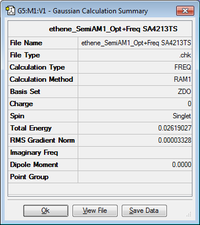
Molecule	Summary	Point Group	Energy/Hartrees
		D2h	0.026190

The LOG file can be found here.

HOMO	LUMO

The visualised MOs show that the HOMO is symmetric and the LUMO is antisymmetric. Thus the HOMO-LUMO combinations are of correct symmetry.

Transition Structure

Optimisation

The optimised structures were put together and spaced at a distance of 2.26 Å. This guess structure was then optimised using TSBerny to find the new optimised transition structure for the cycloaddition:

Molecule	Summary	Energy/Hartrees
		0.111655

The LOG file can be found here.

(You could have included script to show the vibration with the jmol. For example, adding <script>frame 71; vibration 2</script> to the jmol will produce the result below Tam10 (talk) 15:00, 10 January 2016 (UTC))

The energy summary shows an imaginary frequency. This had a value of -956.38 cm^-1. The vibration follows the movement of ethene towards butadiene, as expected for the transition state, with synchronous bond formation at both ends:

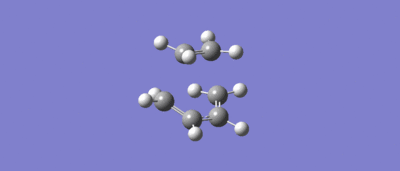
Additionally we can view the MOs of the transition state structure:

HOMO	LUMO

The molecular orbitals of the transition state show that the HOMO is antisymmetric and the LUMO is symmetric with respect to the plane. As said before the HUMO-LUMO combinations of the reactants were of the right symmetry. The HOMO of the TS is a combination of ethene's LUMO and butadiene's HOMO. The LUMO of the TS is a combination of ethene's HOMO and butadiene's LUMO.

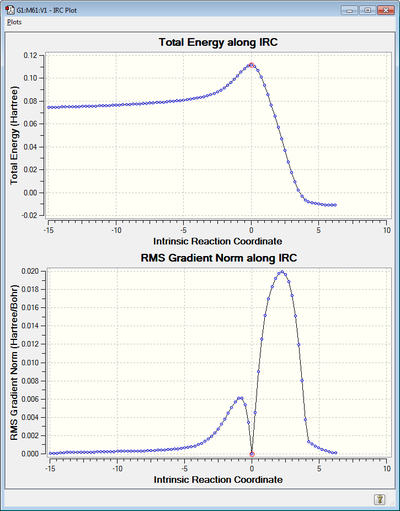
IRC Analysis

IRC Analysis	Reaction Pathway

The LOG file can be found here.

As before the reaction pathway was calculated in both directions as the reaction isn't symmetric. As shown above the transition state is at a maximum and our reactants and products are achieved as you fall off this peak. The RMS Gradient tends to zero on both sides of the transition state however the total energy plot shows that the reactants are a higher energy than the cyclohexene product, thus we can predict the reaction is exothermic.

Geometry Analysis

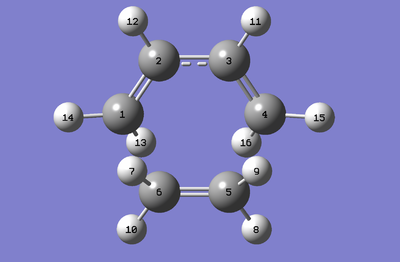
Atoms	Distance/Å
C1-C2	1.38191
C2-C3	1.39747
C3-C4	1.38187
C4-C5	2.11954
C5-C6	1.38296
C6-C1	2.11899

The average bond lengths for double and single bonds are 1.33 and 1.54 Å respectively. In this reaction we're breaking double bonds and forming two single bonds between C1-C6 and C4-C5. The values from the calculation give a value of 2.12 Å, which shows a reduction in length from the set at 2.26 Å. The Van der Waals radii for a single carbon is 1.70 Å, as our transition structure has optimised the bond length to 2.12 Å this indicates that there are bonds being formed as we're within twice the Van der Waals radius of a carbon atom. The C1-C2 and C3-C4 show lengthening from the double bond literature value of 1.33 Å, as we're breaking π bonds we would expect this lengthening. Also between C2-C3, a π bond is being formed, thus we see a reduction from 1.54 Å, but it hasn't yet reach 1.33 Å. Therefore we can conclude there are bonding interactions are happening, and coupled with the imaginary frequency we can conclude this is a transition state.

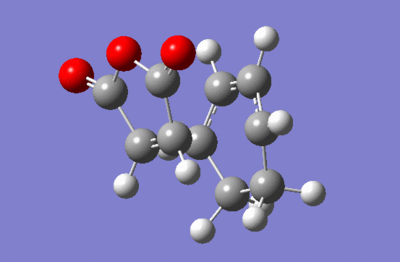
Maleic Anhydride and cyclohexadiene

For this reaction, QST2 was used to find the transition structure. This required optimising reactants separately and combined, and also optimising the exo and endo transition states.

Maleic Anhydride

Molecule	Summary	Point Group	Energy/Hartrees
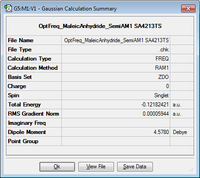
		CS	-0.121824

The LOG file can be found here.

HOMO	LUMO

The visualised maleic anhydride's MOs show that the HOMO is symmetric and the LUMO is antisymmetric.

1,3-cyclohexadiene

Molecule	Summary	Point Group	Energy/Hartrees
		C2	0.027711

The LOG file can be found here.

HOMO	LUMO

The visualised MOs show that the HOMO is antisymmetric and the LUMO is symmetric. Thus the HOMO-LUMO combinations are of correct symmetry.

Exo and Endo

Exo

Molecule	Summary	Point Group	Energy/Hartrees
		C1	-0.159909

The LOG file can be found here.

Endo

Molecule	Summary	Point Group	Energy/Hartrees
		C1	-0.160171

The LOG file can be found here.

Optimisation of the Exo Cycloaddition

As before, the reactants were placed 2.2 Å apart and arranged to look similar to the exo product that was placed in the product window. As for the boat structure above both the product and reactant molecules were labelled to match. This guess structure and product were optimised to QST2 via the Semi-Empirical AM1 method:

Molecule	Summary	Point Group	Energy/Hartrees
		C1	-0.050419

The LOG file can be found here.

HOMO	LUMO

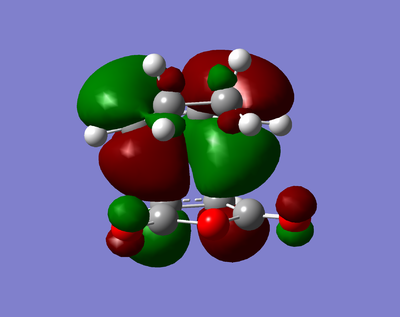
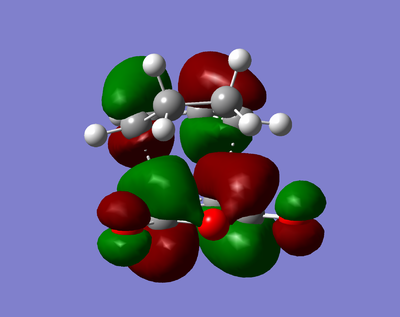
The visualised MOs show that both the HOMO and the LUMO is antisymmetric.

The energy summary above shows one imaginary frequency, confirming that a transition state has been obtained. The frequency was found at -812.20 cm^-1.

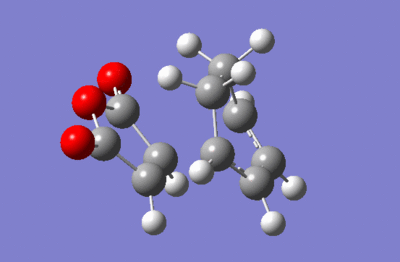
This vibration points to our calculation achieving a viable transition state as we see the double bond of the dienophile and the terminal carbons of the diene move towards each other.

IRC Analysis

When IRC analysis was performed the calculation unexpectedly shows the product as the starting point - the TS input doesn't have bonds between reactants as seen in the frame where the plot hits minimum energy. Nonetheless the IRC still follows an expected shape discounting this point. The GIF produced is the backwards reaction but shows the reaction we expect in reverse, with the maleic anhydride and 1,3-cyclohexadiene approaching and forming the exo product.

(This glitch in the IRC is probably due to GaussView reading an error file. Don't worry though - what you have is sufficient evidence of a successful TS calculation Tam10 (talk) 15:20, 10 January 2016 (UTC))

IRC Analysis	Reaction Pathway

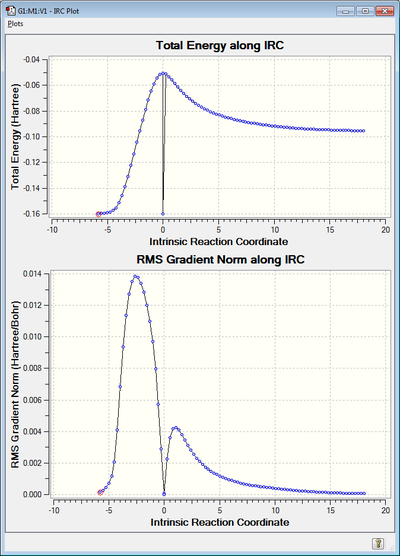
The LOG file can be found here. The GJF file is also attached here, this calculation resulted in an error.

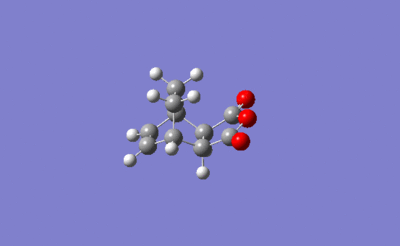
Optimisation of the Endo Cycloaddition

Molecule	Summary	Point Group	Energy/Hartrees
		C1	-0.051505

The LOG file can be found here.

HOMO	LUMO

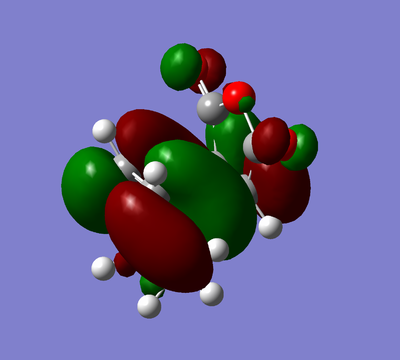
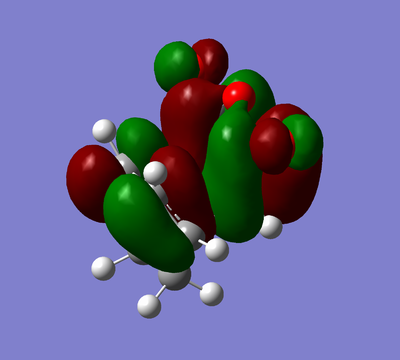
Again the HOMO and the LUMO are antisymmetric.

The energy summary above shows one imaginary frequency, confirming that a transition state has been obtained. The frequency was found at -806.37 cm^-1.

Again this vibration is a viable transition state as we see the double bond of the dienophile and the terminal carbons of the diene move towards each other.

IRC Analysis

When IRC analysis was performed, again the calculation used the product before expected. The IRC shows the transition state going into the products.

IRC Analysis	Reaction Pathway

The LOG file can be found here. The GJF file is also attached here, this calculation also resulted in an error.

	AM1 Semi-Empirical
	Electronic energy/Hartrees	Sum of electronic and zero-point energies/Hartrees	Sum of electronic and thermal energies/Hartrees
		at 0 K	at 298.15 K
Exo TS	-0.050419	0.134880	0.144881
Endo TS	-0.051505	0.133494	0.143682
Cyclohexa-1,3-diene	0.027711	0.152502	0.157726
Maleic anhydride	-0.121824	-0.063347	-0.058193

	AM1 Semi-Empirical
	at 0 K	at 298.15 K
ΔE Exo TS/ kcal/mol	28.690339	28.455651
ΔE Endo TS/ kcal/mol	27.820612	27.703267

The tables above show that the endo transition state has a lower energy than the exo TS. This in itself favours thermodynamic reactions, but additionally the activation energy for the endo TS is smaller which favours the kinetic pathway. The endo transition structure is lower in energy and as such is the preferred transition path.

(I'm not sure what you mean by "favours thermodynamic reactions". If you're talking about the thermodynamic product you'd need to calculate the reaction enthalpy Tam10 (talk) 15:20, 10 January 2016 (UTC))

Secondary Orbital Overlap Effect

	LUMO+1	LUMO+2
Exo TS
Endo TS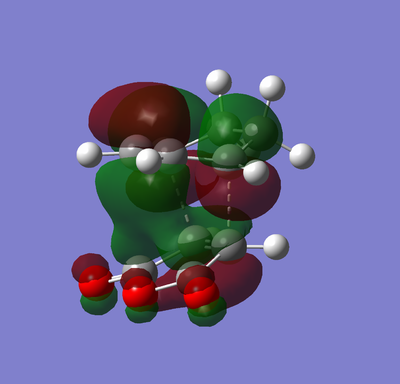

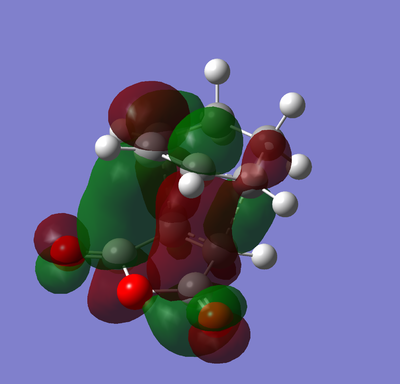
Visualising the MOs of the exo and endo transition states can help explain why the expected thermodynamically most stable exo product doesn't dominate. Orbital interactions outside of those needed for the cycloaddition provide the stabilisation that makes the endo TS more stable. These are available when the π systems of the two halves of the cycloaddition can favourably interact after the cycloaddition has occured. In this case the π* of the C=Os in the maleic anhydride part is interacting favourably with the π system in the 1,3-cyclohexadiene part. This is only available in the cis-endo product as the double bond created in the cycloaddition is roughly parallel enough to have a favourable overlap with the π* lobes from the two C=Os. For the trans-exo product these two systems are positioned at opposite sides of the molecule therefore it is more difficult for these to interact strongly.

(This is a good case. However, performing AM1 calculations for the endo and exo product would reveal that the endo is actually lower in energy Tam10 (talk) 15:20, 10 January 2016 (UTC))

Geometry Analysis

Exo	Endo

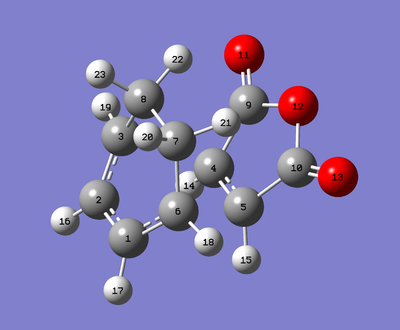
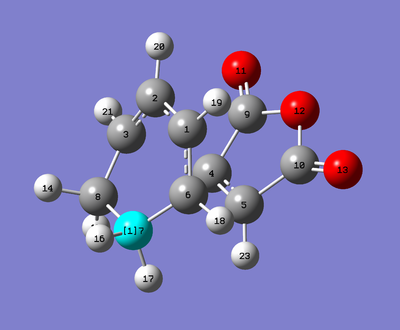
Atoms	Exo Bonds/Å	Endo Bonds/Å
C1-C2	1.39(674)	1.39(724)
C2-C3	1.39(448)	1.39(304)
C3-C4	2.16(809)	2.16(249)
C4-C5	1.41(010)	1.40(849)
C5-C6	2.17(268)	2.16(228)
C1-C6	1.39(423)	1.39(304)
C7-C8	1.52(232)	1.52(295)
C6-C7	1.48(963)	1.49(058)
C5-C10	1.48(802)	1.48(923)
C22-C11(exo) /C20-C11(endo)	2.69(573)	3.31(690)

Whilst the distances are all essentially the same - as Gaussian's bond length accuracy can only be trusted to 2 decimal places, the C5-C6 distance differs by 0.01040 Å, which is greater than any of the other distances. This should come as no surprise as these are the bonds being formed and so are at the mercy of multiple factors. Both transition states have a bond making distance of less than twice the carbon Van der Waals (VdW) radius so we can assume there is bonding interactions happening for both. But the endo TS has the shorter C5-C6 bond of the two TSs indicating that there is greater bonding interaction occuring at its transition state than for the exo TS. This can be rationalised by the secondary orbital overlap effect discussed above. Additionally the substituents of the exo and endo TSs play a role in lengthening the bond making length, C22-C11 (for exo) is within the VdW radii of H (1.20) and O (1.52), which would indicate a disfavourable steric interaction causing lengthening of the C5-C6 bond. In the endo TS the CH₂CH₂ fragment is on the other side of the molecule and the planar CHCH hydrogens are outside of the VdW radii distance.

(Good discussion here Tam10 (talk) 15:20, 10 January 2016 (UTC))

Conclusion

This experiment analysed the Cope Rearrangement of 1,5-hexadiene, the cycloaddition of cis-butadiene and ethene, and the cycloaddition of 1,3-cyclohexadiene and maleic anhydride using Gaussian 09W. During our analysis of the Cope Rearrangement, we found the energies of the conformers of 1,5-hexadiene and compared levels of theory with the 'anti2' conformer. It was found that DFT/B3LYP/6-31G(d) was a more accurate method when looking at the geometry of the optimised conformers due to its method of calculation compared to HF/3-21G. The boat and chair transition structures were both studied and found that the chair structure was of a lower energy (and therefore activation energy) and that the 6-31G(d) level of theory was more accurate to experimental values. In all cases the transition state was confirmed via obtaining a negative frequency which told us, the vibration produced an energy maximum.

For the Diels Alder reactions, all calculations were done at the Semi-empirical/AM1 level of theory. This uses experimental data to forego some of the calculations in the previous methods to reduce computation time. The first reaction studied showed us the concerted nature of the reaction and some of the symmetry considerations that need to be passed in order for a successful reaction. The reaction between maleic anhydride and 1,3-cyclohexadiene was more informationally rich. From this reaction we studied the secondary orbital effect, and used it to rationalise why the cis-endo transition state was dominant over the trans-exo state - something we couldn't previously do without a computational analysis. Additionally we saw how the exo form had more steric clash between the oxygen lone pairs and the hydrogens on the sp³ carbons. AM1 provided to be sufficient for these two reactions, however it wouldn't perform as accurately for more complex systems or for transition metals, thus a more expensive method would be necessary.

To improve upon this study it may be beneficial to try all the transition state methods (TSBerny and RCE) for the two Diels Alder reactions. This would allow us to have a larger range of data for comparison, to conclude the best method for each case. Also testing the limits of the QST2 input could have beneficial to see how far from the optimal transition structure our guess could be.