Rep:Mod:Rickiezhang
NH3 Molecule
Molecule Summary
| Molecule | NH3 |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final Energy | -56.55776873 au |
| RMS Gradient | 0.00000485 |
| Point Group | C3V |
| N-H Bond Length | 1.01798 Å |
| H-N-H Bond Angle | 105.741° |
Item Table
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Jmol and Optimisation file
NH3 molecule |
Vibrations of the molecule
We expect 6 modes from the 3N-6 rule where N is the number of atoms in the molecule. (In this case 4)
There are 2 degenerate modes at frequencies of 1693.95 (Modes 2 and 3) and 3589.82 (Modes 5 and 6).
The bending modes are 1,2 and 3 and the stretching modes are 4,5 and 6.
Mode 4 is highly symmetrical.
Mode 1 is the umbrella mode.
Since there are 2 pairs of degenerate modes we would expect to see 4 bands in the experimental spectrum of gaseous ammonia but, we only see 2 bands as the modes 4,5 and 6 are too low in infra-red intensity to be seen in the spectrum.
There are no negative frequencies, which shows that the molecule is fully optimised.
Charges on the molecule
We can see that Nitrogen contains a -1.125 charge and the Hydrogens have a charge of 0.375.
This is expected as Nitrogen is a very electronegative element so is electron withdrawing creating a more negative charge on itself, as a result the Hydrogens bear a positive charge.
N2
Molecule Summary
| Molecule | N2 |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final Energy | -109.52412868 au |
| RMS Gradient | 0.00000060 |
| Point Group | D*H |
| N-N Bond Length | 1.10550 Å |
| N-N Bond Angle | 180° |
Item Table
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Jmol and Optimisation file
N2 molecule |
Vibrations of the Molecule
This molecule is fully optimised as there are no negative frequencies.
We use the 3N-5 rule as this is a linear molecule which gives us 1 expected mode as shown in the table.
The mode is a stretching mode that is symmetrical.
There is no dipole-dipole moment so no band would be seen in the spectrum of N2.
H2
Molecule Summary
| Molecule | H2 |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final Energy | -1.17853936 au |
| RMS Gradient | 0.00000017 |
| Point Group | D*H |
| H-H Bond Length | 0.74279 Å |
| H-H Bond Angle | 180° |
Item Table
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Jmol and Optimisation file
H2 molecule |
Vibrations of the Molecule
There is no negative frequencies for H2 showing it has been fully optimised.
There is one mode shown that is a symmetrical stretching mode as predicted from the 3N-5 rule.
The infra-red frequency is 0 showing that there is no dipole-dipole moment for a band to be seen in the spectrum of H2.
Haber-Bosch process energy calculation
E(NH3)= -56.55776873 au
2*E(NH3)= -113.1155375 au
E(N2)= -109.52412868 au
E(H2)= -1.17853936 au
3*E(H2)= -3.53561808 au
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.05579074 au
ΔE= -146.48 KJ/mol
The ammonia product is more stable because the reaction is exothermic which results in a decrease in energy from the reactants to the product.
ClF Molecule
Molecule Summary
| Molecule | ClF |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final Energy | -559.94269578 au |
| RMS Gradient | 0.00014211 |
| Point Group | C*V |
| Cl-F Bond Length | 1.66434 Å |
| Cl-F Bond Angle | 180° |
The bond length of ClF calculated isn't identical to the literature value of 1.628[1] but the difference is within experimental error.
Item Table
Item Value Threshold Converged? Maximum Force 0.000246 0.000450 YES RMS Force 0.000246 0.000300 YES Maximum Displacement 0.000433 0.001800 YES RMS Displacement 0.000613 0.001200 YES
Jmol and Optimisation file
ClF molecule |
Vibrations of the Molecule
The 3N-5 rule predicts one mode for the CLF molecule.
This modes is seen to be a stretching mode with the Fluorine atom stretching more than the Chlorine atom probably due to the fact that Fluorine is much lighter.
We would expect to see 1 band in an experimental spectrum of gaseous ClF.
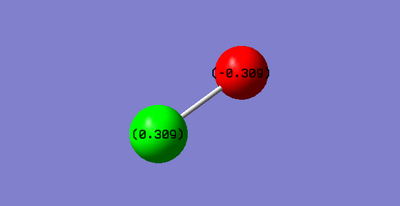
Charge on the Molecule
The Fluorine atom has a charge of -0.309 and the Chlorine atom has a charge of 0.309.
This is as expected as Fluorine is more electronegative so would be more electron withdrawing and hence develop a relative negative charge while the Chlorine being less electronegative will have a relative positive charge.
Molecular Orbitals
MO 1 with energy of -101.63074 au
This is an occupied non-bonding orbital made up of the 1s of Fluorine. This is the lowest energy MO and is deep in energy.
MO 4 with energy of -7.31069 au
MO 6 with energy of -7.29213 au
These are occupied non-bonding orbitals made up of the 2p orbitals of Chlorine. From the energies of the MOs we can deduce that MO 4,5 and 6 are degenerate.
MO 7 with energy of -1.21864 au
This is an occupied sigma bonding orbital formed from the constructive overlap of the 2s of Fluorine and the 3s of Chlorine. This forms a bonding and anti-bonding pair with MO 8 which both are involved in bonding. We can see that the Fluorine atom contributes more to bonding than the Chlorine atom since it is more electronegative and hence deeper in energy. Electronegative atoms such as Fluorine contribute more to bonding MOs and contribute less to anti-bonding MOs.
MO 8 with energy of -0.83311 au
This is an occupied sigma anti-bonding orbital formed from the destructive overlap of the 2s of Fluorine and the 3s of Chlorine. There is more Cl character in this MO as the less electronegative atom, in this case Chlorine, contributes more to anti-bonding MOs.
MO 9 with energy of -0.52314 au
This is an occupied sigma bonding orbital formed from the constructive overlap of the 2p of Fluorine and the 3p of Chlorine. This is a bonding and anti-bonding pair with MO 14.
MO 10 with energy of -0.46713 au
This is an occupied pi bonding orbital formed from the constructive overlap of the 2p of Fluorine and the 3p of Chlorine. This MO has degenerate energy with MO 11. This is a bonding and anti-bonding quadruplet along with MO 11, 12 and 13 which are all involved in bonding.
MO 12 with energy of -0.32855 au
This is an occupied pi anti-bonding orbital formed from the destructive overlap of the 2p of Fluorine and the 3p of Chlorine. This has degenerate energy with MO 13. This is one of the HOMOs along with MO 13.
MO 14 with energy of -0.12150 au
This is an unoccupied sigma anti-bonding orbital formed from the destructive overlap of the 2p of Fluorine and the 3p of Chlorine. This is the LUMO of the molecule and is relatively high in energy.