Jump to content

Rep:Mod:Rhysxyz

From ChemWiki

Conformational Analysis using Molecular Mechanics

The Hydrogenation of Cyclopentadiene Dimer

Cyclopentadiene dimerises to give the endo-conformer, 2, rather than the exo-conformer, 1.

Endo-dimer Exo-dimer
Cyclopentadiene endo-dimer
Cyclopentadiene exo-dimer

To determine whether the dimerisation is under kinetical or thermodynamic control, we can look at the energy of each of the conformers. A kinetically controlled reaction has a low energy transition-state (TS); a thermodynamically controlled reaction has a low energy product state.
Using Avagadro the energies of the two conformers can be calculated by optimising geometries (forcefield = MMFF94):

Dicyclopentadiene Energies (Table 1)
Conformer Total Energy / kcal/mol
Endo 58.19067
Exo 55.37345

The calculations show that the exo- product is lower in energy than the endo- product. Therefore, it is reasonable to deduce that the reaction proceeds via a kinetic pathway where the TS of the endo- product is lower than the TS for the exo- product. The endo-adduct is lower by approximately 3 kcal/mol, which is in agreement with the calculations ran by Caramella et al[1]. This paper illustrates a great reaction profile of the endo- and the exo- pathways, showing that my theory that the endo- TS is lower than the exo- TS is in agreement with their work.

Endo-dicyclopentadiene can be hydrogenated at either of the two double bonds to give either molecule 3 or molecule 4.

Hydrogenated Dicyclopentadiene Energies (kcal/mol) (Table 2)
Molecule Total Energy Bond Stretching Angle Bending Stretch Bending Torsional Out-of-plane Bending Van der Waals Electrostatic
3 51.22782 3.23053 29.79484 -1.96214 1.64622 0.02135 13.62462 5.12068
4 41.25800 2.82562 24.66315 -1.65740 -0.38272 0.00023 10.66219 5.14693

Looking at the calculations produced in Avagadro, 4 is lower in every energy category (except electrostatic energy as neither molecule is significantly charged). This proves that 4 is much more easily obtained in comparison to 3 and it can be deduced that this is the thermodynamic product. The main difference in energies comes from the bond-stretching energies, a reasonable assumption for this being particularly high in molecule 3 is that the double bond present in the 6-membered ring will cause it to deviate away from its desired angle, more so than a double bond in a 5-membered ring will(such as molecule 4).

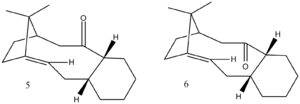
Atropisomerism in an Intermediate related to the Synthesis of Taxol

Two isomers, 5 or 6, are formed as an intermediate in the synthesis of the drug Taxol [2], and has been shown to have anti-cancer effects for the ovaries as well as other body parts.[3]. The carbonyl group can be facing either up or down and when left standing the carbonyl isomerises to the more stable form ; this is known as atropisomerism. To determine the more stable form, calculations were run on Avagadro using an MMFF94s force-field. The results are presented in Table 3, and it is clear that 6 is the most stable isomer; the largest contributor to the difference in energies is the 'total angle bending energy' where there is a 16.46956 kcal/mol difference.

It might be useful to note that calculations ran on different diastereoisomers (isomerism around the alkene) also gave different energies, if we label molecules 5 and 6 diastereoisomers as molecule 5.5 and 6.5 respectively, you can see that the energy of 6 and 6.5 are remarkably close, however alkene 5 and 5.5 have a larger difference.
To try and further minimise the energy of molecule's 5 and 6, I altered the cyclohexane ring so that it was in chair-conformation instead of the twist-boat-conformation. My prediction was correct and the cyclohexane being in the chair-conformation does lower the energy as shown in Table 3.
For all instances the major difference between the two carbonyl isomers is the angle bending energy, which shows that the carbonyl facing down must give the least conformational strain regardless of the geometry elsewhere in the ring.
Isomer 5
Isomer 6

Relative Energies (kcal/mol) of 5 and 6 (Table 3)
Molecule Total Energy Angle Bending Energy
5 86.82836 30.91186
6 66.29272 19.01612
5.5 80.12850 34.07231
6.5 67.34749 23.14255
Molecule 5 chair-conformation 75.09588 25.92035
Molecule 6 chair-conformation 61.18817 16.89811

The alkene reacts abnormally slowly, this is largely due to the fact it is what is known as a 'bridgehead olefin'. This makes it a hyperstable alkene, so stable it has a negative olefin strain energy.[4]. Olefin strain energy is defined as "the difference between the strain energy of an olefin and its respective hydrocarbon"[5] Calculations in Avagadro show that the hydrogenated molecule of 6 has a higher overall energy of 76.44244kcal/mol; a difference of +10.14972 kcal/mol. The angle bending energy of this hydrocarbon is 24.96307 kcalm/mol, this is 5.94695 kcal/mol less stable than olefin 6. This shows that hydrogenation may be unfavourable and is further evidence that the alkene is of a high stability.

Spectroscopic Simulation using Quantum Mechanics

Molecule 7 is a derivative of molecule 6, the formation is shown in a paper by Paquette[6].
Calculating the geometry at the density function level (DFT) using Guassian we can simulate a prediction for the NMR of this molecule. Below are the list of peaks for the 1H and 13C NMR from the calculations in comparison to the literature values[6]. The calculations had the following properties: Theory = B3LYP; Basis = 6-31G(d,p); Solvent = chloroform.

Molecule 7
Molecule 7
NMR comparisons between calculations[7] and literature[6] (Table 4)
1H 13C
Calculation Literature Calculation Literature Difference
ppm No peaks ppm Multiplet Relative integration ppm ppm ppm
5.38 1 5.21 m 1 212.245 211.49 0.755
3.36 1 3.00-2.70 m 6 148.90 148.72 0.18
3.14 1 2.70-2.35 m 4 118.549 120.9 2.351
3.05 1 2.20-1.70 m 6 89.0635 74.61 14.4535
2.98 1 1.58 t 1 67.5725 60.53 7.0425
2.83 1 1.50-1.20 m 3 56.3133 51.30 5.0133
2.54 1 1.10 s 3 55.5398 50.94 4.5998
2.45 2 1.07 s 3 50.093 45.53 4.563
2.21 1 1.03 s 3 46.8327 43.28 3.5527
2.11 2 44.4622 40.82 3.6422
1.99 4 41.299 38.72 2.579
1.86 1 37.6786 36.78 0.8986
1.77 2 36.2853 35.47 0.8153
1.68 1 32.0826 30.84 1.2426
1.53 2 29.0631 30.00 0.9369
1.41 1 28.6958 25.56 3.1358
1.31 1 25.8626 25.52 0.5126
1.11 4 25.213 22.21 3.003
0.98 2 23.2864 21.39 1.8964
21.7426 19.83 1.9126
13C NMR, Molecule 7

13C
Both spectra have the same number of peaks. All shifts are pretty close except that of calculated 89.0635 ppm with a literature value of 74.61 ppm leaving a difference of over 14 ppm; and calculated 67.5725 ppm with a literature value of 60.53 ppm leaving a difference of 7.0425 ppm. Aside from this all shifts are within 5 ppm of each other. There could be several reasons for the difference in shifts, one reason could be that my simulated conformation is not an exact match of that synthesised in the literature. However, looking at the Jmol above for molecule 7 and the literature reference given, I think it is safe to say that my molecule is the same as the literature's. So perhaps the molecule synthesised wasn't entirely the correct conformation.

1H NMR, Molecule 7

1H
The calculation gives 30 peaks for the hydrogen NMR, looking at the molecule I do not agree that all protons are in separate environments (for example, the 3 protons on the methyl group coming off the cyclohexane ring). However, the literature lists only 8 environments, whereas I think there are more environments than that. The reason being is that the literature has grouped several of the peaks into multiplets without giving specific splitting pattern. The paper was published in 1990 suggesting the advanced NMR analysis software available to us now was not present, so large groupings of peaks would have been hard to define into separate environments.
The actual NMR shifts seem to be quite different though, this could mean that our two molecules are quite different; there is something else to consider though, and that is that the article is using deuteriated benzene as a solvent, whereas I used chloroform(CDCl3 ), this could alter all the shifts, so it is hard to tell what the main issue in the difference in spectra are.



Analysis of the Properties of the Synthesised Alkene Epoxides

This section will focus on the two alkenes, dihydronaphthalene and trans-stilbene, and their epoxidation reactions when using the Shi catalyst or the Jacobsen catalyst.

Crystal structures of the catalysts

Shi Catalyst

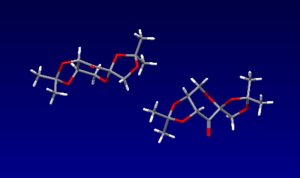
There are three anomeric carbons in the Shi catalyst, all the bond lengths of the anomeric carbons to the oxygen atoms have been analysed using the Cambridge crystal database (CCDC) and Mercury software; I have listed them in the image below (all lengths in Angstroms). As you can see the lengths of each anomeric C-O bond is different except for one. This could be due to the anomeric effect. This is where the alpha anomer is in a resonance structure by donation of an oxygen lone pair into the correctly aligned antibonding C-O orbital, Π*C-O. When this dissociated resonance form is present we can expect one C-O bond to have partial double bond character, i.e. a stronger, shorter bond, and the other C-O bond to have partial non-bonding character, i.e. a longer, weaker bond. For the anomeric carbon where the two bond lengths are 1.403A, we can assume there is not much, if any, resonance occuring, therefore it might not even technically be defined as an anomeric carbon.


Jacobsen Catalyst

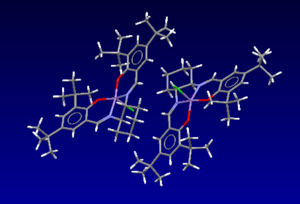
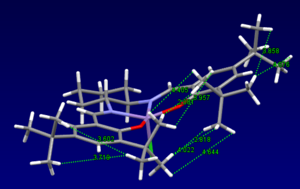
Below are the bond distances between different hydrogens on the two tert-butyl groups in the centre of the molecule. I have listed the shortest bonds. Two times the van der Waals radii for hydrogen is 2.1A[8], anything less than this is repulsive, and anything greater (although not too much greater or no interaction will be seen at all) is attractive, therefore these hydrogen interactions between the adjacent tert-butyl groups will be slightly attractive, lowering the overall energy of the molecule.

Distances between tert-butyl hydrogens(Table 5)
Inter-atomic bond distance
2.081
2.818
3.957
4.022
4.405
4.644







NMR of epoxides

Dihydronaphthalene oxide

1H NMR
1H NMR dihydronaphthalene oxide[9]

As you can see the literature and the calculated hydrogen NMR shifts for dihydronaphthalene oxide are very similar. They both have the same number of environments; the main difference being that the literature values are approximately 0.2-0.3ppm less than the calculated values, apart from that the two spectra seem to be very similar

1H NMR Dihydronaphthalene oxide(Table 6)
No peaks Shift/ppm[9] Lit. peaks/ppm Lit. multiplicity & int.[10]
1 7.615 7.34 m, 1H
2 7.390 7.14-7.23 m, 2H
1 7.251 7.01 d, 1H
1 3.560 3.78 d, 1H
1 3.483 3.65 t, 1H
1 2.967 2.65-2.70 m, 1H
1 2.267 2.45 dd, 1H
1 2.210 2.31-2.39 m, 1H
1 1.873 1.60-1.70 m, 1H
13C NMR
13C NMR dihydronaphthalene oxide[9]

Once again, the two spectra are very similar for dihydronaphthalene oxide, most peaks in the literature being almost exactly the same as calculated! Looking at the 1H and 13C spectra, I think it is safe to say that the simulated molecule is very much in agreement with the actual synthesised molecule from the literature.

13C NMR Dihydronaphthalene oxide(Table 7)
No peaks Shift/ppm[9] Lit. peaks/ppm[10]
1 135.4 135.6
1 130.4 131.5
1 126.7 128.5
1 123.8 127.4
1 123.5 127.3
1 121.7 125.1
1 52.8 54.1
1 52.2 51.7
1 30.2 23.4
1 29.1 20.8

Trans-stilbene oxide

1H NMR
1H NMR trans-stillbene oxide[11]

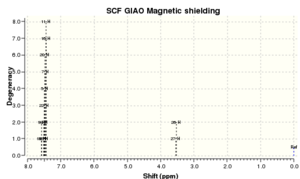
All the peaks once again match the literature, except the literature has grouped 10 hydrogens into the same environment as a singlet. These 10 hydrogens will correspond to the aromatic hydrogens and will all have similar environments, however they will be slightly different. Perhaps they have been grouped up in the reference because the spectra is not as well resolved due to lack of analysis software in the past. This of course leaves the final two hydrogens which will be on the two sp2 hybridised carbons bridging the two benzene rings together.

1H NMR Stilbene oxide(Table 7)
No peaks Shift/ppm[11] Lit. shifts/ppm Lit. multiplicity & int.[12]
2 7.571 7.4 s, 10H
8 7.507-7.450
2 3.54 3.88 s, 2H
13C NMR
13C NMR trans-stillbene oxide[11]

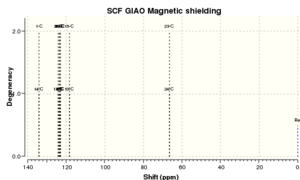
The two spectra for the carbon-13 NMR are in close agreement for this molecule. The literature is missing 2 peaks that the calculation showed. The six low-field shifts will correspond to the carbon atoms in the aromatic ring, and maybe the literature could not resolve each of the individual peaks and so grouped two of them togethr - this would make sese as you cannot integrate a carbon-13 NMR and so peaks can easily be hidden.

13C NMR Stilbene oxide(Table 8)
No peaks Shift/ppm[11] Lit. shifts/ppm[13]
2 134.1 137.1
2 124.2 128.5
2 123.5 128.2
2 123.2 125.5
2 123.1
2 118.3
2 66.4 62.7

Absolute configurations of the Epoxides

There are three ways to measure the absolute configuration of the epoxides. These are:

  1. Optical rotation at a specific wavelength (optical Rotatory Power)/at various wavelengths (Optical Rotatory Dispersion)
  2. Electronic circular dichroism
  3. Vibrational circular dichroism

However, I will only be using optical rotation as the other two methods are not available in the third year synthesis laboratory.
(It is worth noting that the optical rotation of compounds can vary quite differently from report to report in the literature)

  • Literature optical rotation for dihydronaphthalene oxide (S,R) = [Alpha]22D=21 deg[14]
  • Calculated optical rotation for dihydronaphthalene oxide (S,R) = [Alpha] ( 5890.0 A) = 35.91 deg[15]
The literature and the calculation are in close agreement both positive rotation. The reason for the slight difference could be due to the difference in temperature and concentration.


  • Literature optical rotation for stilbene oxide (R,R) = [Alpha]25D= 319.8 deg[16]
  • Calculated optical rotation for stilbene oxide (R,R) = [Alpha] ( 5890.0 A) = 298.20 deg[17]
The two optical rotation are once again in good agreement, I think it is safe to assume the difference is for the same reasons mentioned above.

The close optical rotation of both compounds to the literature suggests the simulated compound is of the correct configuration.

Transition state analysis of β-methyl styrene

For both catalysts the total energy for each transition state, after it has been corrected for entropy and zero-point thermal energies, has been identified. The difference between the free energy of two diastereoisomers has then been calculated and converted to K (the ratio of concentrations of the two transition states based on their energy difference) using the well-known equation ΔG=−RTlnK. Finally, the enantiomeric excess can be calulcalated using the equation ee=K−1K+1.[18]

Shi catalysis for trans-β-methyl styrene epoxidation

Free energies of trans-β-methyl styrene epoxidation TS's[19] (Table 9)
TS# (R,R) (S,S) Delta(G) K ee %
Hartree kJ/mol
1 -1343.022970 -1343.017942 0.005028 13.201014 0.0048528 99.0
2 -1343.019233 -1343.015603 0.003630 9.530565 0.0213493 95.8
3 -1343.029272 -1343.023766 0.005506 14.456003 0.0029242 99.4
4 -1343.032443 -1343.024742 0.007701 20.2189755 0.0002856 99.9

For each diastereoisomeric pair, the (R, R) conifguration is the enantiomer in excess by over 95%. Diastereoismomer pair 4 shows that the (R, R) configuration is almost 100%!

Jacobsen catalysis for trans- and cis-β-methyl styrene epoxidation

Free energies of trans-β-methyl styrene epoxidation TS's [19](Table 10)
TS# (S,S) (R,R) Delta(G) K ee %
Hartree kJ/mol
1 -3383.262481 -3383.253816 0.008665 22.7499575 0.0001028 99.98
2 -3383.257847 -3383.254344 0.003503 9.1971265 0.0244249 95.2

For the Jacobsen epoxidation of trans-β-methyl styrene, the (S, S) configuration is the enantiomer in excess, once again by over 95% in both cases. This is the opposite to the Shi catalyst which gave predominately the (R, R) enantiomer.

Free energies of cis-β-methyl styrene epoxidation TS's[19] (Table 11)
TS# (S,R) (R,S) Delta(G) K ee %
Hartree kJ/mol
1 -3383.259559 -3383.251060 0.008499 22.3141245 0.0001226 99.98
2 -3383.253442 -3383.250270 0.003172 8.328086 0.0346870 93.3

The epoxidation of cis-β-methyl styrene using the Jacobsen catalyst gives the (S, R) enantiomer in excess, one that is almost 100% and the other slightly lower at 93.3%, this is the lowest ee value seen for the epoxidation ran on this experiment. However it is still highly selective.


For both the Jacobsen and the Shi catalysis reactions the free energy difference between each diastereoisomeric pair appears to be minimal, differing only after the second decimal point. However, we can see that this small difference in free energies should not be over-looked as it can largely affect the outcome of the percentage of each enantiomer in the product.


Non-Covalent Interactions (NCI)

NCI interactions, as suggested by the abbreviation, involve interactions between atoms that are non-covalent. This can include, for example, hydrogen bonds and electrostatic interactions. We can simulate NCI's on molecules, and analyse the semi-qualitative result. One such simulation is below for the transition state between the active Shi catalyst and (R, R) trans-β-methyl styrene.[20]

Orbital

The different colours indicate different attractions. The colour code is as follows: blue = very attractive; green = mildly attractive; yellow = mildly repulsive; red = strongly repulsive. The analysis shows that the interactions between the catalyst and the substrate are many mildy attractive interactions. There is also a multi-coloured ring, this is indictative of a covalent bond forming in the transition state, this type of interaction is usually ignored and is considered to be a semi-covalent interaction. Within the catalyst itself there are some small but very strong repulsive interactions in the 5-membered rings. This would appear to be from the repulsion between the two highly electronegative oxygen atoms present in both of the rings. In the 6-membered rings on the catalyst and the substrate there are 'yellow', mild-repulsive interactions. This is also probably because of repulsion between the atoms in the ring being forced to be quite close together; however this repulsive interaction is not as strong as the previously mentioned because of the absence of highly electronegative atoms.

Investigating the Electronic topology (QTAIM)

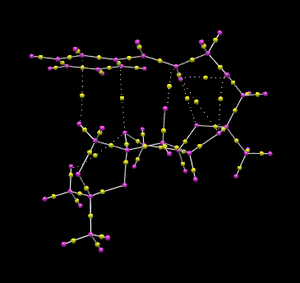
QTAIM is complementary to the NCI analysis, as it includes NCI analysis, but mainly focuses on electron-density in covalent interactions (i.e. very strong attractive interactions classified as bonds). Using QTAIM we can locate the BCP (bond critial point) which has the curvature appropriate for a specific bond. You can also see weak non-covalent BCP's, such as hydrogen bonds.
Below is a QTAIM analysis of the same transition state that was used for NCI analysis (Shi catalyst on (R, R) trans-β-methyl styrene).[20] The small yellow spheres are the BCP's between two atomic nuclei, their quantitative position (space coordinates) are currently not available due to computational limitations, so have to be estimated qualitatively. The yellow spheres connected by dotted lines are the non-covalent interactions. Interesting points of the QTAIM analysis:

  • There is an NCI between a Shi hydrogen and a substrate carbon; and an NCI between a Shi and a substrate hydrogen.
  • BCP's are closer to carbon atoms in a carbon-oxygen bond.
  • BCP's are closer to hydrogen atoms in a carbon-hydrogen bond.
trans-β-methyl styrene QTAIM analysis
trans-β-methyl styrene QTAIM analysis

Suggesting new candidates for study

Searching Reaxys.com I found an alkene Pulegone which could be used to study the epoxidation reaction in a similar fashion. This compound could be of interest because it can epoxidate[21] to form two isomers. It also has different reported ORP's, this could be checked using computational methods.

References

  1. ↑ P. Caramella, P. Quadrelli and L. Toma, Journal of the American Chemical Society, 2002, 124, 1130-1131. DOI: DOI:10.1021/ja016622h
  2. ↑ S. W. Elmore and L. A. Paquette, Tetrahedron Letters, 1991, 32, 319-322. DOI: DOI:10.1016/S0040-4039(00)92617-0 )
  3. ↑ F. A. Holmes, A. P. Kudelka, J. J. Kavanagh, M. H. Huber, J. A. Ajani and V. Valero, in Taxane Anticancer Agents, American Chemical Society, Editon edn., 1994, vol. 583, pp. 31-57. DOI: DOI:10.1021/bk-1995-0583.ch003
  4. ↑ A. B. McEwen and P. v. R. Schleyer, Journal of the American Chemical Society, 1986, 108, 3951-3960. DOI: DOI:10.1021/ja00274a016
  5. ↑ W. F. Maier and P. V. R. Schleyer, Journal of the American Chemical Society, 1981, 103, 1891-1900. DOI: DOI:10.1021/ja00398a003
  6. ↑ 6.0 6.1 6.2 L. A. Paquette, N. A. Pegg, D. Toops, G. D. Maynard and R. D. Rogers, Journal of the American Chemical Society, 1990, 112, 277-283. DOI: DOI:10.1021/ja00157a043
  7. ↑ DOI:10042/27477
  8. ↑ A. Bondi, The Journal of Physical Chemistry, 1964, 68, 441-451. DOI: DOI:10.1021/j100785a001
  9. ↑ 9.0 9.1 9.2 9.3 DOI:10042/27479
  10. ↑ 10.0 10.1 D. Xiong, X. Hu, S. Wang, C.-X. Miao, C. Xia and W. Sun, European Journal of Organic Chemistry, 2011, 2011, 4289-4292. DOI: DOI:10.1002/ejoc.201100512
  11. ↑ 11.0 11.1 11.2 11.3 DOI:10042/27478
  12. ↑ K. S. Ravikumar, F. Barbier, J.-P. Bégué and D. Bonnet-Delpon, Tetrahedron, 1998, 54, 7457-7464.DOI: DOI:10.1016/S0040-4020(98)00396-2
  13. ↑ D. J. Phillips, J. L. Kean and A. E. Graham, Tetrahedron, 2013, 69, 6196-6202. DOI: DOI:10.1016/j.tet.2013.05.036
  14. ↑ R. W. Draper, D. Hou, R. Iyer, G. M. Lee, J. T. Liang, J. L. Mas, W. Tormos, E. J. Vater, F. Günter, I. Mergelsberg and D. Scherer, Organic Process Research & Development, 1998, 2, 175-185. DOI: DOI:10.1021/op970121s
  15. ↑ DOI:10042/27480
  16. ↑ B. Wang, X.-Y. Wu, O. A. Wong, B. Nettles, M.-X. Zhao, D. Chen and Y. Shi, The Journal of Organic Chemistry, 2009, 74, 3986-3989. DOI: DOI:10.1021/jo900330n
  17. ↑ DOI:10042/27481
  18. ↑ S. T. Schneebeli, M. L. Hall, R. Breslow and R. Friesner, Journal of the American Chemical Society, 2009, 131, 3965-3973. DOI: DOI:10.1021/ja806951r
  19. ↑ 19.0 19.1 19.2 Data taken from calculations ran by Henry Rzepa: https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:organic#Assigning_the_absolute_configuration_of_the_product
  20. ↑ 20.0 20.1 Rzepa, Henry S. (2013): Gaussian Job Archive for C21H28O7. figshare.DOI:10.6084/m9.figshare.738028
  21. ↑ W. Reusch and C. K. Johnson, The Journal of Organic Chemistry, 1963, 28, 2557-2560. DOI:10.1021/jo01045a016 10.1021/jo01045a016
Retrieved from "https://chemwiki.ch.ic.ac.uk/index.php?title=Rep:Mod:Rhysxyz&oldid=817792"