Rep:Mod:Rhubarbicon2802
Hydrogenation of a Cyclopentadiene Dimer
Relative energy of dimer 1
31.8834kcal/mol
Pentahelicene |
Relative energy of dimer 2 Stretch: 1.2285 Bend: 20.8763 Stretch-Bend: -0.8293 Torsion: 9.5092 Non-1,4 VDW: -1.5645 1,4 VDW: 4.3327 Dipole/Dipole: 0.4490
Total Energy: 34.0018 kcal/mol 34.0018kcal/mol
Pentahelicene |
Relative energy of dimer 3 Stretch: 1.2324 Bend: 18.8641 Stretch-Bend: -0.7625 Torsion: 12.2469 Non-1,4 VDW: -1.5627 1,4 VDW: 5.7523 Dipole/Dipole: 0.1631
Total Energy: 35.9337 kcal/mol
35.9937kcal/mol
Pentahelicene |
Relative energy of dimer 4 Stretch: 1.0963 Bend: 14.5074 Stretch-Bend: -0.5493 Torsion: 12.4972 Non-1,4 VDW: -1.0507 1,4 VDW: 4.5124 Dipole/Dipole: 0.1407
Total Energy: 31.1540 kcal/mol
Pentahelicene |
When comparing pairs 1 and 2 and 3 and 4, the optimised forms of the conformations give very different energy values. From the values obtained, dimer 1 is more thermodynamically stable than dimer 2 and dimer 4 is more thermodynamically stable than dimer 3. However, it has been found that dimer 2 is more readily formed than dimer 1. This means that the cyclodimerisation of cyclopentadiene is kinetically, rather than thermodynamically controlled. This means that the aspect of thermodynamic stability is overidden by the fact that the transition state is more stable in dimer 2 than it is in dimer 1.
The question is, however which one of the double bonds of dimer 2 is more easily hydrolysed? This can be determined, by first comparing the data obtained from dimers 3 and 4 with the data obtained from dimer 2. First of all, when comparing overall energies, as expected, the total energy of 2 is higher than both 3 and 4. This makes sense, as in a reaction the products should be of lower energies than the reactants. However, the total energy of 4 is much lower than 3. When these energy values were broken down into their individual compenants, it was seen that there was only one value that made all of the difference between 4 and 3: the bending coefficient. This was much higher in 3 than it was in 4. This means that the double bond in 3 has a great deal more trouble bending than it does in dimer 4, as this is the only difference between the two molecules. However, what cannot be determined is just how much of that bending energy can be attributed to those double bonds alone. To find this out, calculations were carried out on another molecule that had neither of the two double bonds. Although this is only an approximation, as this actually increased the energy ( because of the torsion), this could be a useful way of finding out just how much of the bending energy is from the double bonds. The bending energy of dimer 2 is 20.8763 and that of the molecule without double bonds is 12.78 (both kcal/mol). Subtracting this value from both the bending energies of 3 and 4 shows that the double bond in 4 is almost 3 times more favourable than the double bond in dimer 3. This means that the hydrogenation of that more strained double bond would be most thermodynamically favourable.
The above can be explained by the fact that double bonds are stabilised, by the interaction between the π* and the σC-H bond. For this interaction to take place, the groups on the alkene must be eclipsed. However, this results in A1,3 eclipsed compression, as the adjacent groups get too close. The alkene in dimer 3 is higher than it is in dimer 4, because the bridging C-C bond between the ring is forcing the two groups closer together than they would like. The distance across the ring when there is a bridging carbon is 2.3Å- when there is no bridging carbon, it is 2.8Å. This phenomenon can also be shown when comparing the angles of the double bonds in dimers 3 and 4. The bond angle in dimer 3 is 108o; the bond angle in dimer 4 is 112o. The larger bond angle shows that the groups are further apart, meaning they repel each other less.
Stereochemistry of Nucleophilic Addition to a Pyridinium Ring
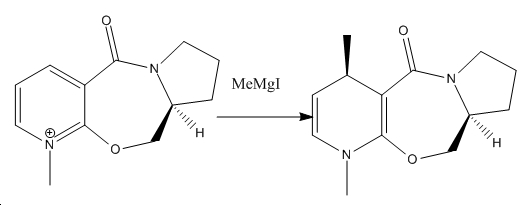
In the first reaction, a Grignard reagent is used to deliver a methyl group to the ring that is adjacent to the carbonyl group. The geometry of this can be rationalised, by the intermediate that the Grignard reagent forms with the reactant. 7
Pentahelicene |
Stretch: 0.9516 Bend: 6.5675 Stretch-Bend: 0.1067 Torsion: 9.3764 Non-1,4 VDW: -2.7113 1,4 VDW: 12.1556 Charge/Dipole: 2.1652 Dipole/Dipole: -4.0303
Total Energy: 24.5815 kcal/mol
This shows the stereochemistry of the reactant (total energy 24.5815kcal/mol). This model shows that the carbonyl group is not in the same plane of symmetry as the aromatic ring. Indeed there is an angle of 40o between the two planes. This will certainly have an effect when the actual reaction is carried out.
When the Grignard reagent reacts with this reactant, there are two possible outcomes to the reaction shown below:
Pentahelicene |
In this case, the methyl group that has been added on by the Grignard reagent is coming out of the page.
Stretch: 1.4357 Bend: 14.3820 Stretch-Bend: 0.1626 Torsion: 6.0176 Non-1,4 VDW: -2.2702 1,4 VDW: 13.2624 Dipole/Dipole: -4.0153
Total Energy: 28.9747 kcal/mol
The other possibility is having the methyl group going in with respect to the aryl group as shown below:
Pentahelicene |
Stretch: 1.5243 Bend: 14.6230 Stretch-Bend: 0.1955 Torsion: 6.2000 Non-1,4 VDW: -1.8440 1,4 VDW: 13.5294 Dipole/Dipole: -4.0156
Total Energy: 30.2126 kcal/mol
Thermodynamically, the former is favoured over the latter, as is seen by the calculated relative energies of the molecules. However, so as to determine whether this reaction is kinetically, or thermodynamically controlled, the actual mechanics of the reaction has to be determined to find which of these is the predominant product.
Pentahelicene |
As can be seen from this model, the coordinated Mg creates a very bulky group (N.B. this is not the actual model of this molecule, as the software used could not process the Mg atom). This is due to the fact that Grignard reagents coordinate in a tetrahedral manner when in a solution, which in the presence of this reactant would result in the carbonyl oxygen also being used as a coordination site. 7This carbonyl oxygen is already outside of the plane of the aromatic ring by 40 degrees (most likely because of the lone pairs interacting with the delocalised ring). This would explain why the methyl group migrates in the opposite orientation with respect to the carbonyl oxygen. The stereochemistry of the rest of the molecule remains unchanged. As it happens, the 7-membered ring is so rigid that only the two conformations shown are possible. 7
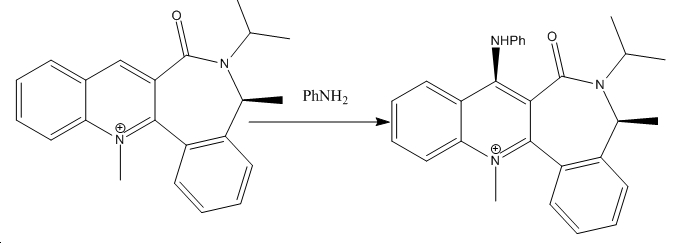
Reaction 2
In this reaction, phenylamine acts as a nucleophile on a quinoliunium salt. The angle between the plane of the aromatic ring and the carbonyl oxygen in this case is 43o. When this molecule is optimised, it is found that it twists about the 7 membered ring. Ideally, this whole system ought to be planar, so as to allow delocalisation, yet here there is an angle of 47o between the quinoline portion of the molecule and the other aromatic ring. This is because a fully planar system would bring the R groups too close, which would result in repulsive forces. Stereochemically, the most favoured conformation would be one in which the aromatic rings are at right angles to each other. However, this is offset by the energetic benefits of having as much delocalisation as possible between the rings. This twist results in atropisomers.
Stretch: 1.6980 Bend: 6.7368 Stretch-Bend: 0.3458 Torsion: -6.4816 Non-1,4 VDW: -1.7830 1,4 VDW: 17.4526 Charge/Dipole: 2.3920 Dipole/Dipole: -4.7915
Total Energy: 15.5691 kcal/mol
The reaction of this molecule with phenylamine results in an even more twisted molecule. Indeed the angle between the quinoline group and the phenyamine group is 85o- only 5o off a complete right angle. This is because this particular group is so bulky that any energetic gains from delocalisation would be offset by steric hindrance.
The total energy of this molecule is 19.994kcal/mol
Pentahelicene |
Stereochemistry and Reactivity in the Synthesis of Taxol
Taxol could be found in two possible conformations: one with the carbonyl sticking upwards and the other with it sticking downwards. So as to determine which is the most likely to be found, the energies of both were minimised and compared.
This led to the realisation that it was indeed the one with the carbonyl group sticking down that was the more stable.
Pentahelicene |
Stretch: 2.5561 Bend: 10.7187 Stretch-Bend: 0.3265 Torsion: 19.6274 Non-1,4 VDW: -1.3138 1,4 VDW: 12.5503 Dipole/Dipole: -0.1811
Total Energy: 44.2840 kcal/mol
Pentahelicene |
Stretch: 2.6641 Bend: 15.9045 Stretch-Bend: 0.3929 Torsion: 18.3154 Non-1,4 VDW: -1.2106 1,4 VDW: 12.7343 Dipole/Dipole: 0.1435
Total Energy: 48.9441 kcal/mol
In both case, the alkene groups are very stable and only react very slowly. This has several reasons: first of all, they have substituents on three of the four positions- these being very bulky substituents. Another reason is that alkenes tend to react as nucleophiles, which means that attack comes about by electrons being put into the HOMO. The HOMO in this case would be the π* orbital, which is sterically protected.
How one might induce Peptide Hydrolysis
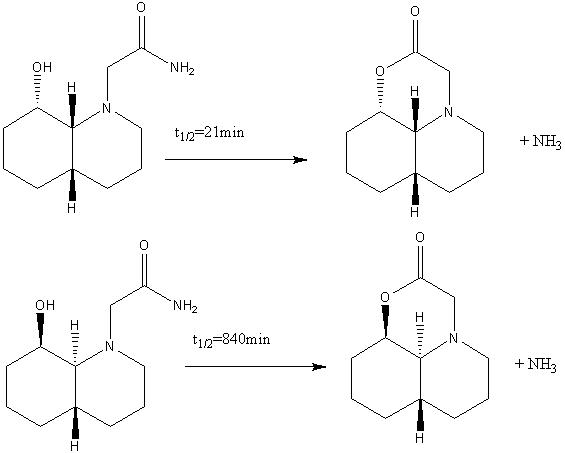
Usually the hydrolysis of a peptide bond can take anything up to 500 years. However, enzymes create such an ideal environment for this reaction to happen that the bond can be broken in less than a second. Peptide hydrolysis has been found to take place with a lactone intermediate. 1 Synthetically there are two methods in which this intermediate can be generated; one of them takes 21 min, the other 840 min. How can this be rationalised? To find this out, the relative energies, as well as geometries of the molecules in the two reactions below had to be found, using ChemBio3D. This reaction was specifically tailored, so that the rotation of the molecules are resticted, without introducing any extra strain. 1
The reactant of the first reaction is a cis-decalin. However, in the above reaction scheme, is not clear is whether the ring N-substituent is in an equatorial, or in an axial position.
Stretch: 1.7827 Bend: 4.9778 Stretch-Bend: 0.5919 Torsion: 13.8664 Non-1,4 VDW: -7.7012 1,4 VDW: 12.0984 Dipole/Dipole: -4.7840
Total Energy: 20.8320 kcal/mol
In the above case, the N-subtituent was placed into the equatorial position and then the molecule was optimised. The most trouble with the software was encountered whilst trying to stop the OH group from being in the same orientation as the hydrogens between the rings.
cisdecalin |
So as to have an objective comparison, the same was done with the N-substituent in the axial position. Particular difficulty was found when trying to create molecules that were NOT exactly the same after optimisation.
Stretch: 1.6450 Bend: 7.2855 Stretch-Bend: 0.6650 Torsion: 16.7735 Non-1,4 VDW: -6.0028 1,4 VDW: 11.8815 Dipole/Dipole: -6.6215
Total Energy: 25.6260 kcal/mol
cisdecalin |
When comparing the two possible reactant conformers, it is clear that the former (equatorial) conformer is more thermodynamically stable than the latter. What is also visible from the models is that the NH2 group is in the correct position to engage in hydrogen bonding with the carbonyl oxygen in both of the conformations.
The product of this cis-decalin reaction was then examined, so as to determine its most likely geometry. When putting the N-substituent in the equatorial position, the following values were obtained:
Stretch: 1.2775 Bend: 9.0488 Stretch-Bend: 0.1095 Torsion: 14.9422 Non-1,4 VDW: -3.1168 1,4 VDW: 9.7610 Dipole/Dipole: -4.3996
Total Energy: 27.6225 kcal/mol
While examining this model, it was realised that putting the N-substituent in the axial posistion would not be possible if the remaining geometry were to be retained. Indeed, it would create such a strained system that it would not be favourable in any way for the product to adopt this conformation.
The same reaction in the the trans-decalin conformation is significantly slower than its cis-decalin analogue. Why this is the case can only be related to the stereochemical difference between the two conformations.
The reactant of the second reaction could have the N-substituent in either an axial, or in an equatorial position.
The axial conformation yielded the following results:
Stretch: 1.3799 Bend: 2.9327 Stretch-Bend: 0.3887 Torsion: 11.5535 Non-1,4 VDW: -5.8325 1,4 VDW: 9.4021 Dipole/Dipole: -5.0377
Total Energy: 14.7866 kcal/mol
This is already a much lower value than what was seen in the cis-decalin case. As can be determined from the model (the pink "atoms" are actually lone pairs of electrons), there is hydrogen bonding in this case.
cisdecalin |
Now the equatorial position was tried and the following results were obtained:
Stretch: 1.5310 Bend: 3.3572 Stretch-Bend: 0.4894 Torsion: 6.4632 Non-1,4 VDW: -6.4862 1,4 VDW: 9.7754 Dipole/Dipole: -3.1455
Total Energy: 11.9846 kcal/mol
As it happens, this is of an even lower energy than before. However, this in no way means that it is necessarily this form of the reagent that goes on to react.
cisdecalin |
The product too could be a mixture of two conformers. Below is the one with an equatorial N-substituent.
Stretch: 1.4225 Bend: 7.3785 Stretch-Bend: 0.5716 Torsion: 8.0410 Non-1,4 VDW: -3.2714 1,4 VDW: 16.1205 Dipole/Dipole: 4.6556
Total Energy: 34.9183 kcal/mol
The same molecule, but with the N-substituent in the axial position was constructed:
Stretch: 1.1968 Bend: 7.7703 Stretch-Bend: 0.5966 Torsion: 4.6411 Non-1,4 VDW: -3.3568 1,4 VDW: 14.7978 Dipole/Dipole: 4.2782
Total Energy: 29.9240 kcal/mol
cisdecalin |
This is significantly lower than the equatorial conformer.
In both cases, it is the equatorial conformation that is preferred (i.e. lower in energy). This agrees with the literature 1. However, in the latter case (the trans-decalin), this conformation does not allow hydrogen bonding to take place, as the nitrogen group is not in the same plane as the carbonyl. When comparing the first to the second reaction, part of the reason that the former reaction has a much shorter half life than the latter can be attributed to hydrogen bonding. This intramolecular hydrogen bond is of particular significance, as it has been suggested that it is this orientation that activates the hydroxyl oxygen that is attacking the nitrogen group.1. In the former reaction, both the axial and the equatorial molecules have hydrogen bonding between the carbonyl group and the NH2 group. In the latter reaction, there is only hydrogen bonding when the NH2 is in the axial position.
When comparing the relative energies of the second reaction, it is found that the equatorial conformer is higher in energy than the axial conformer. This would suggest that there would be more of the latter than the former. However, the axial conformer does not have intramolecular hydrogen bonding that could activate the attacking group. This is of no particular consequence, as the Curtin-Hammet principle states that: " the major conformer in the starting material may not be the most reactive". This must mean, however that there is a significant energy penalty when this reaction is supposed to proceed, as most of the reactant will be in the form of the equatorial conformer. This probably is the key factor when explaining why the first reaction proceeds far more quickly than the latter.
Another reason for the rapidity of the first reaction is because the reagents (both axial and equatorial) are much higher than the corresponding trans-decalin analogues. This plays an important role when the actual energies of the products are compared with the reactants. In the first reaction, there is not much of a difference in energy- if anything, the energies of the products are lower than those of the reactants. In the second, this is not the case- they are actually higher in energy. This must mean that the conformers in the former reaction are more strained, which means that the reaction relieves this strain, which is most likely what drives it forward at this pace. The conformers in the latter case are subject to a lot less strain, which means that the reaction does them no great energetic favours. The reactions carried out agree with what is stated in the literature. 1
The fact that it does not take 500 years to hydrolyse these peptide bonds can be attributed to the fact that the relevant groups are put into the correct orientation. This is actually what happens in the enzyme when this reaction takes place in less than a second- the freely rotating peptide is locked into place and forced to react. These particular molecules react in such a way, as the shape has been restricted so that the reacting groups are in the correct position. This particular reaction is first order and the reason it reacts is because the activation energy has been lowered.
Regioselective Addition of Dichlorocarbene
Regioselective Addition of Dichlorocarbene
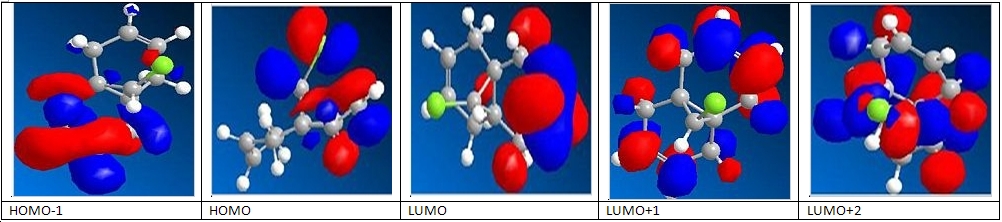
So as to determine how this molecule would react were it being attacked by an electrophile, it was necessary to create a model of the molecular orbitals. This was done for the HOMO-1, the LUMO, LUMO+1 and the LUMO+2. As it is acting as an electrophile, it is the HOMO that we are most interested in, as this is the most accessible orbital for electrons to be taken from. Below are the molecular orbitals generated using the MOPAC function of ChemBio3D. As can be seen from the screen shots, the HOMO is largely concentrated on the double bond exo to the chlorine. This means that it is this position that is first hydrogenated, as it is where the HOMO is concentrated and it is not sterically hindered.
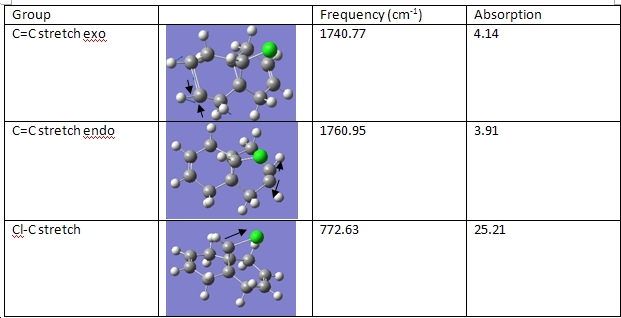
By submitting the optimisation to SCAN and then the frequency (the function in which both are supposed to occur at once failed), the vibrations for the dichlorocarbene, as well as the monohydrogenated dichlorocarbene were found. Particular interest was payed to the C=C and the Cl-C stretching frequencies, as the two differently hydrogenated compounds were compared in this manner.
Dichlorocarbene
Monohydrogenated Dichlorocarbene
As can be seen from the C=C and C-Cl stretching frequencies, these are different when the molecule has two, or one double bond. Indeed, with the dichlorocarbene, the stretching frequencies are not the same; with the monohydrogenated dichlorocarbene, the double bond's stretching frequency is different to that in the dichlorocarbene in the same position.
The frequencies of the C=C groups in the dichlorocarbene can be rationalised as follows: the exo C=C group has a lower frequency than the endo C=C group, because electron density is being donated from the π orbital to the C-Cl σ* orbital. From what can be seen from the MO depiction of this molecule, these orbitals would be in the correct orientation for this to happen. This would decrease the strength of the C=C double bond, as electron density is removed from the bond, by this form of delocalisation. As the electrons are being donated into the antibonding orbital of the C-Cl bond, this would too be weakened. Weaker bonds result in lower stretching frequencies:
The monohydrogenated dichlorocarbene does not have this double bond exo to the C-Cl bond. This would explain why the C-Cl stretch is now stronger than it previously was: there is no more overlap between the п orbital and the σ* orbital, meaning that this bond is not weakened.
Research Project
Regiocontrolled Addition of Arylboronic Acids to Allenes Using Palladium and Platinum Catalysts5
Many reactions produce an array of different products that then need to be separated out, so as to be able to isolate the desired product. Some of these products are easier to separate than others- particularly difficult are isomers. Many different techniques are utilised to characterise and then to separate the different molecules. Many isomers may look very similar and have very similar properties, yet they can have huge differences when it comes to delivering the results that they have been tailored to deliver. The pharmaceutical industry is certainly no stranger to these difficulties. Indeed, there have been several examples in which an only slightly different drug has had extremely adverse effects on those who ingested it. One of the most famous examples is thalidomide- a drug frequently prescribed to pregnant women for morning sickness which resulted in many deformed babies. Another example is mefloquine- an antimalarial drug, which is currently sold as a racemic mixture. It is suspected that one of the enantiomers is responsible for fighting the malaria parasite, while the other is responsible for side effects by which around 25% of patients are plagued. 2
The reaction that will be examined is the Regiocontrolled Addition of Arylboronic Acids to Allenes Using Palladium and Platinum Catalysts. In this reaction, several isomers were produced. However, as this was a particularly thorough investigation, only 2 specific reactions will be examined. The first question is: how can they be told apart? The reaction is the following:
The first isotope's IUPAC name is (E)-1-(1-Hydroxycyclohexyl)-2-phenyl-1-propene, the second's IUPAC name is 1-(1-Hydroxycyclohexyl)-2-phenyl-2-propene.
This reaction uses a transition metal catalyst to add an arylboronic acid to an allene. This reaction results in the production of three different products- two of which are isomers of each other (as can be seen by the molecular weight). It is also found that using a different transition metal catalyst changes the relative distribution of these products. This investigation will be on the products obtained when reacting the allene with a platinum-based catalyst ([Pt2(OH)2(PPh3)4][BF4]2 (2), KOH). In this case, the distribution of the products (left to right) is 20%, 2% and 66%.
It must be confessed that in this particular reaction it is very easy to tell the products apart, as they will not only have completely different IR stretching frequencies, but they will also give completely different NMR specta (H, or C13). The two isomers are exactly the same except in one respect: the double bond is differently positioned. This difference would be picked up by IR, as the bending frequency of the C-H of the double bond would be different, due to the different degree of substitution. There would be a difference in the 640-860cm-1 region with the former bend being at a higher frequency. 3
The NMR spectra would be very different from one another. Indeed, this would probably be the best way to tell them apart. A simple HNMR would quickly show which one was which.
The former isotope has The latter isotope has 4 distinct environments (excluding the phenyl group, which shall be ignored). The two vinylic hydrogens are too far away to couple to any of the other protons, so it would show up as a singlet in the 4.6- 5.9 ppm region.
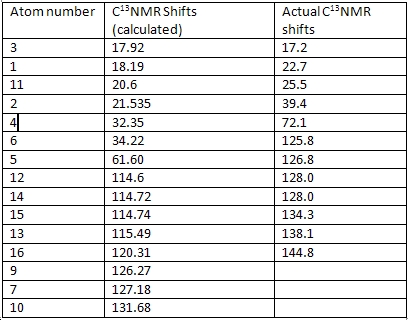
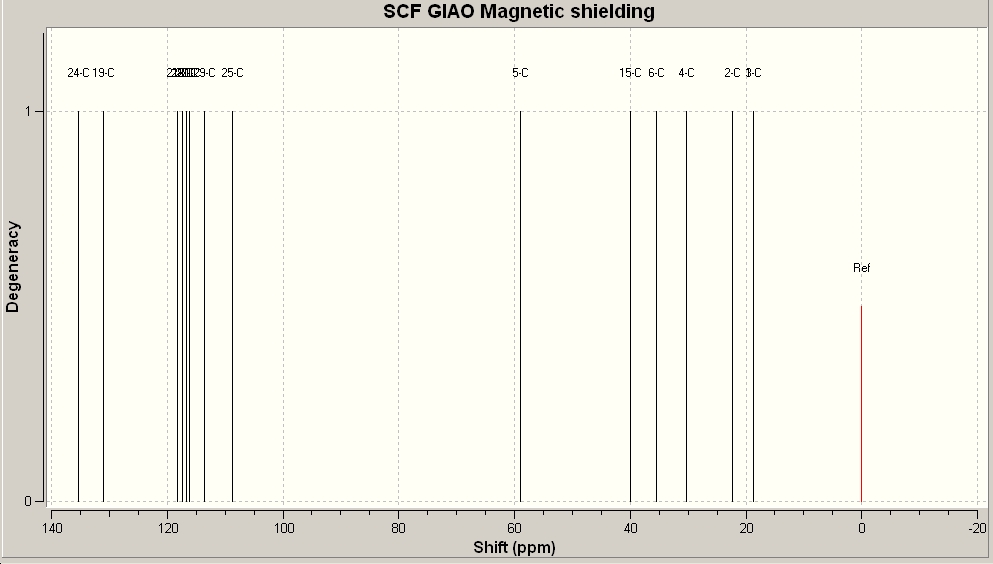
The C13NMR was generated, using GaussView. This was then compared with the actual C13 NMR of this molecule. In this way, the accuracy of the Gaussview optimisation and then the generation of the NMR can be assessed.
The calculated values of the C13 NMR of (E)-1-(1-Hydroxycyclohexyl)-2-phenyl-1-propene were compared with the actual values obtained through experiment. The experimental C13 NMR has fewer values than the calculated NMR, which can be explained by the fact that the program sees the molecule in fragments that have numerical imput values and then uses these values to calculate properties of molecules that exist as separate entities in their own right. The program cannot take all interactions into account and also cannot see that some of the expected shifts might not be present. As the C13 NMR data for this molecule is not particularly well labelled in the literature, it is difficult to correlate the experimental values with the calculated ones. There are three missing values and as the data was so poorly labelled, it is difficult to tell which ones these are. Comparing the values with the calculated ones may also not be wise, as it is unclear as to how accurate they are.
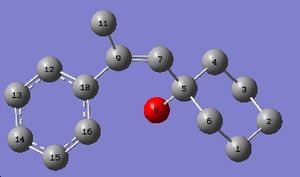
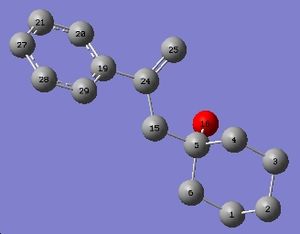
The same was done for the less substituted isomer. As the data was from the same paper, it was equally badly labelled, so the correlation between the values is again difficult. This molecule has even more calculated shifts that do not appear in the experimental NMR. The actual NMRs should be on the supporting information, but there are characters on them that cannot be supported by this computer, which is unfortunate, as these would have had the integrals from which the NMR could be interpreted.
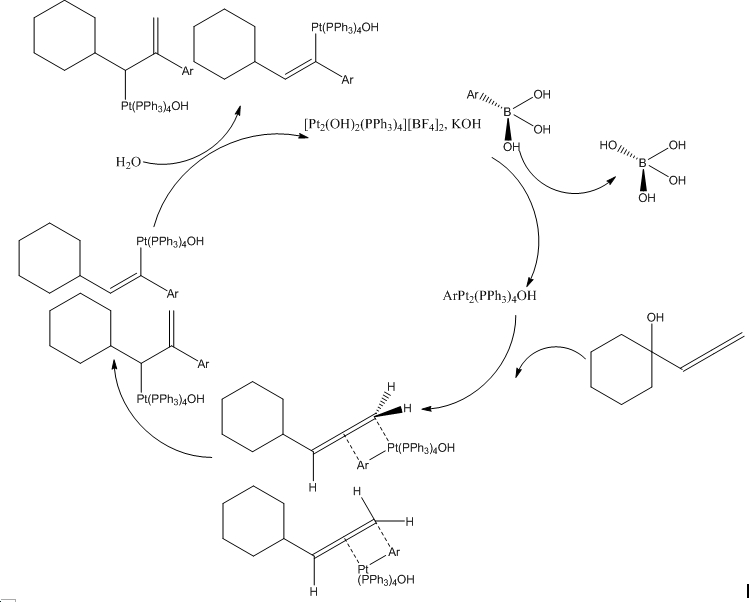
A proposed mechanism for the reaction is as follows. As would be expected, it works in a cycle:
References
1 [http://pubs.acs.org/cgi-bin/abstract.cgi/joceah/2008/73/i16/abs/jo800706y.html Nicolette M. Fernandes, Fabienne Fache, Mari Rosen, Phuong-Lan Nguyen, and David E. Hansen,J. Org. Chem. Vol. 73, No. 16, 2008]
6 Supplementary information of reference 5
7 Arthur G. Schultz, Lawrence Flood, and James P. Springer, J. Org. Chem.; 1986; 51(6) pp 838 - 841