Rep:Mod:RUNAOns3
Module 3
Introductions
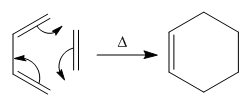
In module one, the problem of predicting whether the major product in a reaction is the kinetic or thermodynamic product was encountered. It was concluded that information regarding the transition states in the formation of the products was needed in order to make any decision in this matter. This computational module aims to calculate the low energy minima and transition states structures of 1,5-hexadiene during a concerted [3+3] sigma-tropic rearrangement, Cope rearrangement. The chair transition state has been found to be at a lower energy compared to the boat.[1] Furthermore, techniques gained in the tutorial part of this module will be used to analyse a Diels-Alder cycloaddition reaction.
 |
Cope Rearrangement of 1,5-hexadiene
Optimization of 1,5-hexadiene
Drawn on Guassview 5.0, anti and gauche conformers of 1,5-hexadiene (structures 1 and 2) were optimized using HF/3-21G level theory with 250 MB memory limit.. The Jmol of the resulting structures is accompanying the image of the conformers. The log files were checked to confirm that the force, and displacement had converged upon optimization. However on calculating the vibrational spectra of these two molecules, it was found that the anti-structure has two imaginary frequencies.Also, the energy of this conformer doesn't match exactly to those in appendix one, its energy is closest to Anti-1. Subsequently another anti structure was drawn and optimized, structure 3. This second anti-1,5-hexadiene corresponds to Anti 1 in the appendix.
| Conformation (Corresponding structure in Appendix) | Total Energy/ a.u. (Mcalmol-1 | RMS Gradient Norm /a.u. | Dipole /Debye | Point Group |
|---|---|---|---|---|
| Structure 1 (Anti 3) DOI:10042/to-11027 | -231.6854 (-145.38) | 0.00012 | 0.00 | C2h |
| Structure 2 (Gauche 2)DOI:10042/to-11028 | -231.6917 (-145.39) | 0.0000072 | 0.3804 | C2 |
| Structure 3 (Anti 1)DOI:/10042/to-11205 | -231.6926 (-145.39) | 0.00001149 | 0.2023 | C1 |
| Structure 4 (Anti 2)DOI:10042/to-11212 | -231.6925 (-145.39) | 0.00003926 | 0.00 | Ci |
| Structure 5 (Gauche 3) DOI:10042/to-11090 | -231.6927 (-145.39) | 0.00000605 | 0.3407 | C1 |
The anti and gauche 1,5-hexadiene shown in structure 1 and 2 at first indicated no symmetry when optimized, but after the structures were symmetrizing the point group was C2h/C1 and C2/C1 respectively.
 |
 |
 |
|
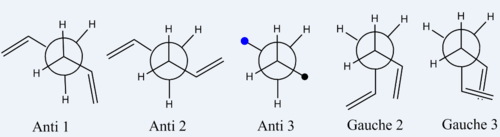
| Newman projections of 1,5-hexadiene conformations use in this report. The blue dot represent a C=C behind the plane of the page and the black dot is the C=C group coming out of the plane of the page. |
Other conformers of 1,5-hexadiene were optimized in the attempt to obtain Gauche 3 structure in appendix 1, these have been noted in table 1. All these structures were re-optimized with Density Function Theory with 6-31G(d) basis set.
| Conformation | Total Energy/ a.u. (kcalmol-1 | RMS Gradient Norm /a.u. | Dipole /Debye | Point Group |
|---|---|---|---|---|
| Structure 1 (Anti 3) DOI:10042/to-11224 | -234.6049(-147.22) | 0.000027 | 0.00 | C2h |
| Structure 2 (Gauche 2)DOI:10042/to-11213 | -234.6107(-145.39) | 0.0000087 | 0.4401 | C2 |
| Structure 3 (Anti 1) DOI:10042/to-11225 | -234.6118 (-147.22) | 0.00001087 | 0.2611 | C1/2 |
| Structure 4 (Anti 2) DOI:10042/to-11215 | -234.6117 (-147.22) | 0.00001343 | 0.00 | Ci |
| Structure 5 (Gauche 3) DOI:10042/to-11214 | -234.6113 (-147.22) | 0.00000382 | 0.3959 | C1 |
Structures 1 and 2 have similar energies. Nevertheless, the anti-conformer is at a slightly higher energy than gauche. Anti-periplanar conformations would have been predicted to have lower energy because such conformers suffer from less steric interactions. Given that, gauche conformations in this situation are of lower energy than the anti, there may be some electronic interactions stabilizing the gauche conformers more than in the anti-structures. It appears that the conformation in which the two double bonds are close to each gives the most stable conformer. The bonds may be able to interact with each favourable thus stabilizing the molecule.
Comparison of HF/3-21G and B3LYP/6-31G(d)
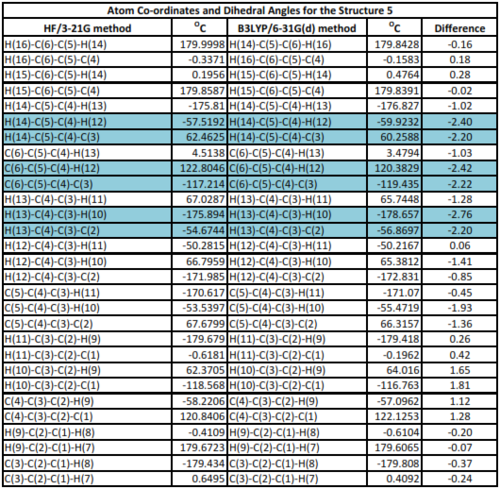
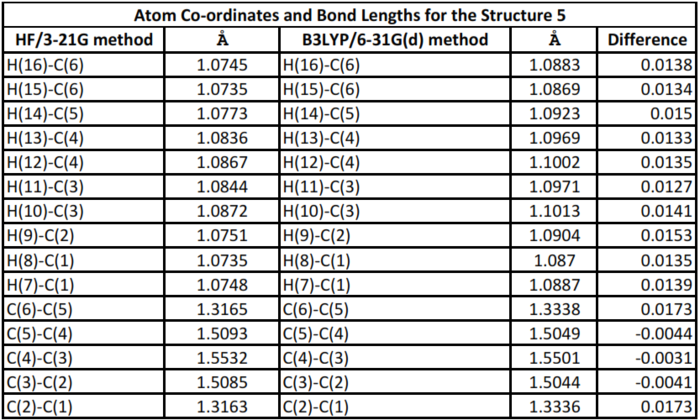
Examining table 3 and 4, the differences between the properties of structure 5 optimised using HF/3-21G and B3LYP/6-31G(d) is clear. Theses difference highlight the reason why energies and geometries of isomeres obtained from different methods and basis sets cannot be compared. Since the B3LYP/6-31G(d) method has a bettter basis set and offers better optimization of the structures, the parameters from method may be taken to be closer to experimental measurements.
|
|
Vibrational Spectra of the Structures using HF/3-21G and B3LYP/6-31G(d)
The vibrational frequencies of the structures mentioned above were calculated confirm successful optimization of the conformers. Unfortunately, this showed that optimization of structure 1 have failed because it had two imaginary frequencies. The vibrational spectra of B3LYP/6-21G(d) optimized strucutre 1 also had imaginary frequencies. This may have been because structure 1 is the transition state between two conformers.Since structure 1 was not fully optimized its thermodynamicc properties will not be calculated.
| Conformation | IR Spectrum from HF/3-21G | IR Spectrum from B3LYP/6-31G(d) |
|---|---|---|
| Structure 1 | 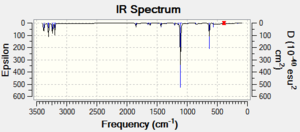 DOI:10042/to-11259 DOI:10042/to-11259 |
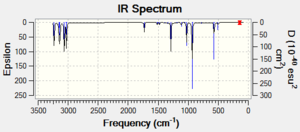 DOI:10042/to-11258 DOI:10042/to-11258
|
| Symmetric C=C stretch /cm-1, Intensity | 1848.88, 0.00 | 1726.89, 0.00 |
| Assymmetric C=C stretch /cm-1, Intensity | 1851.27, 12.54 | 1730.25, 9.80 |
| Structure 2 | 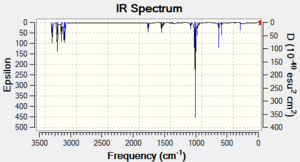 DOI:10042/to-11249 DOI:10042/to-11249 |
 DOI:10042/to-11250 DOI:10042/to-11250
|
| Symmetric C=C stretch /cm-1, Intensity | 1848.68, 31.84 | 11734.37, 7.12 |
| Assymmetric C=C stretch /cm-1, Intensity | 1858.18, 8.73 | 1734.41, 6.76 |
| Structure 3 |  DOI:10042/to-11251 DOI:10042/to-11251 |
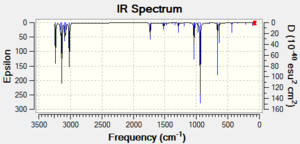 DOI:10042/to-11252 DOI:10042/to-11252
|
| Symmetric C=C stretch /cm-1, Intensity | 1855.95, 6.41 | 1731.96, 4.73 |
| Assymmetric C=C stretch /cm-1, Intensity | 1858.12, 10.17 | 1734.86, 13.55 |
| Structure 4 | 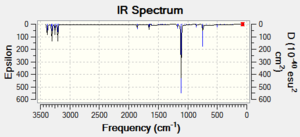 DOI:10042/to-11254 DOI:10042/to-11254 |
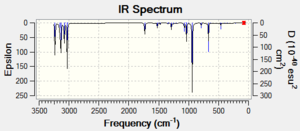 DOI:10042/to-11257 DOI:10042/to-11257
|
| Symmetric C=C stretch /cm-1, Intensity | 1848.88, 0.00 | 1726.89 0.00 |
| Assymmetric C=C stretch /cm-1, Intensity | 1851.27, 12.54 | 1730.25, 9.80 |
| Structure 5 |  DOI:10042/to-11247 DOI:10042/to-11247 |
 DOI:10042/to-11248 DOI:10042/to-11248
|
| One C=C stretch /cm-1, Intensity | 1855.32, 6.96 | 1731.86, 6.89 |
| Other C=C stretch /cm-1, Intensity | 1856.22, 7.01 | 1732.97, 6.13 |
Looking at the table 5 a number of trends can be drawn out. Overall, the carbon-carbon double bond stretches for the Hf/3-21G optimised structures occurs at a higher frequency than the B3LYP/6-21G(d) optimized structures. This is problably due to the quality of the method and basis set used in the calculation. B3LYP/6-21G(d) calculation is able to provide lower energy vibrational frequency for the structures, which is closer to the experimental value.
Another trend which agrees with chemistry intution is the fact that the intensities of the C=C symmetric stretches are very low and often IR inactive. 1,5_hexadiene, like many aliphatic molecules have very small dipole. The difference in electronegativity between carbon and hydrogen is smal hence the bond is no very polar. Carbon-carbon single/double bonds are not polar hence overall the C-C stretches are weak. The C=C symmetric stretch, especially, don't produce much change in dipole because any dipole changes cancel each other out. This cancelling is less effective in the gauche structure because of the bent structure. It must be noted that the double bonds in structure 5, stretch independently unlike in the other conformers.
Analysis of the Thermodynamic Properties of 1,5-Hexadiene
The energies of the molecules in tables 1 and 2 can not be directed compared to experimental data. Thermodynamic parameters calculated fore the structures however can be compared to experimental data; these can be found in the log files of the frequency calculation of the structures.
| Structure | E = Eelec + ZPE | E = E + Evib + Erot + Etrans | H = E + RT | G = H - TS |
|---|---|---|---|---|
| 2 | -231.538704 | -231.531794 | -231.530850 | -231.570132 |
| -234.468284 | -234.460968 | -234.460024 | -234.500011 | |
| 3 | -231.539601 | -231.532645 | -231.531707 | -231.570953 |
| -234.469298 | -234.461966 | -234.461022 | -234.500862 | |
| 4 | -231.539538 | -231.532563 (-231.532566)[2] | -231.531618 | -231.570919 |
| -234.469212 | -234.461856 | -234.460912 | -234.500820 | |
| 5 | -231.539486 | -231.532647 | -231.531703 | -231.570640 |
| -234.468693 | -234.461464 | -234.460520 | -234.500705 |
The energy of the Anti 2 conformation agrees closely to the value in the results table from module 3 wiki page.
E = Eelec + ZPE - the sum of electronic and zero-point energies, (potential energy at 0 K including the zero-point vibrational energy).
E = E + Evib + Erot + Etrans -the sum of electronic and thermal energies (energy at 298.15 K and 1 atm of pressure which includes contributions from the translational, rotational, and vibrational energy modes at this temperature).
H = E + RT -the sum of electronic and thermal enthalpies, ( contains an additional correction for RT, which is particularly important when looking at dissociation reactions).
G = H - TS -the sum of electronic and thermal free energies, (includes the entropic contribution to the free energy).
Hatree Fock/3-21G theory has has been used to optimise different conformations of the 1,5-hexadiene and it has shown the order of stability of structures.
Chair and Boat Transition State
Optimization to TS(BERNY) Transition State Using HF/3-21G Theory Level
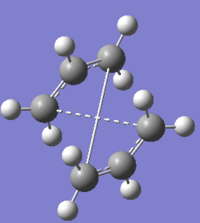
An Allyl fragment was optimized using HF/3-21G theory level DOI:10042/to- . This fragment was copied and pasted twice into a new molecule group window on Gaussview 5.0 and orientated to produce a chair transition state, for the Cope rearrangement of 1,5-hexadiene. The transition state structure has one imaginary vibrational frequency, -817.99 cm-1, this vibration correseponds to the Cope-rearrangement.
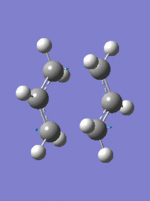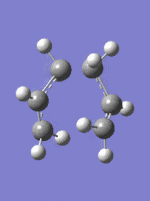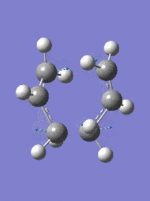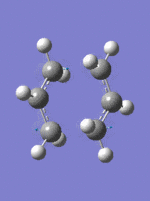
Frozen Coordinates Transition State Optimization method
The guess chair transition structure was copied to a new molecule group window and the distance between the terminal carbons were fixed to 2.2Â and the structure was optimized to a minimum using HF/3-21G method DOI:10042/to-to- . The fragment separations within in double the carbon van der waals radius (3.4Â), therefore interaction between the molecules is possible. The resulting structure was then optimized, with the coordinates of the terminal carbons unfrozen. Subsequently, the distance between the terminal carbons decreases. Again a negative vibration, corresponding to the transition state is observed at -818 cm-1.
QST2 Transition Opimization Method
This method allows optimization to the transition structure by specifying the reactant and the product of the Cope-reaction. For successful completion of this method the atoms of the reactant molecule and the product must correspond, as shown in the image below.
Optimization of the conformers above failed to produce to give the boat transition state, but gives the chair transition state, DOI:10042/to-to-11275 . This is due to the inability of QST2 method to allow rotation around the central carbon atoms. Consequently the structure had to manually adjusted, shown below, for a successful transition state optimization, DOI:10042/to-11276 . Again, an imaginary frequency is observed at -840.14cm-1.Observation of a single vibrational frequency congruent with the reaction step, hence formation of the transition state.
Chair Transition State Intrinsic Reaction Co-ordinate
Rection co-ordinates are often drawn not-to-scale to explain a number of concepts in chemistry, Hammond's postulate, difference between thermodynamic and kinetic product. This excersise allows a reaction co-ordinate to be drawn quantitatively and to observe the changes in the structure as the molecules move through the reaction co-ordinate.
It is impossible to determine which conformations of 1,5-hexadiene optimise to chair and boat transition states. IRC allows the minimum energy pathway from the transition state to be followed to reach the local minimum. The IRC was calculated for the optimized chair (TS(BERNY) transition state structure above).
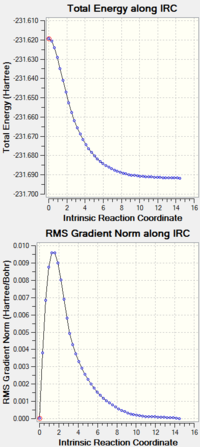 |
Loooking at the IRC, when 50 points is used, it is clear from the gradient graph that the mina has not been located because the gradient if is larger, it should be less than less than 0.001, what's more the energy graph as if it still decreasing. Subsequently, 100 points were used in another IRC calculation. Now, the gradient is low and the energy seems to have reached a minimum. To confirm this another IRc was calculation using 150 points. Without doubt, it can be stated that IRC with 100 point is sufficient and the starting conformaer has been obtained.
Boat Transition State Intrinsic Reaction Co-ordinate
The IRC was also calculated for the boat transition structure. The IRC was run with 100 points, and it graph appears to have reached a minimum, the gradient has plateaued at a small value and the energy of the starting conformer is plateauing, a calculation with more points would have been useful here.
 |
Activation Energies
Vibrational frequencies of the final chair and boat transition structures obtained above were calculated in order to obtain good thermochemistry data.
| HF/3-21G | DFT-B3LYP/6-31G(d) | ||||||
|---|---|---|---|---|---|---|---|
| Structure | Point Group | Electronic energy/ Ha | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | Electronic energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies |
| Chair Transition State | C2h | -231.619322241 | -231.466698 | -231.461339 | -234.61068500 | -231.466698 | -231.461339 |
| Boat Transition State | C2v | -231.61926791 | -231.466686 | -231.461314 | -234.57252007 | -234.430557 | -234.423528 |
| HF/3-21G (298 K)/kcalmol-1 | B3LYP/6-31G(d)(298 K)/kcalmol-1 | |
|---|---|---|
| ΔE (Chair) | +44.69 | +91.0 |
| ΔE (Boat) | +44.71 | +24.59 |
The Activation energy for the chair agrees well lit literatire of 44.7 kcal/mol.[3] From the difference between the Anti 2 (reactant) and the chair transition state is lower than between the reactant and the boat transition state. Hence, it can be concluded that the Cope-rearrangement would take place via a chair transition state.
Diels-Alder Reactions
Diels-Alder reactions are [4+2] cycloaddition reactions between s-cis conjugated dienes and and alkenes or alkynes. During the reaction pi-bonds of the diene and the dienophile interact to form two sigma bonds and one pi-orbital. Interaction of the frontier orbitals of the diene and dienophile can either be allowed or forbidden. Allowed interactions describe the favourable interaction between the frontier orbitals of the diene and the dienophile. Forbidden interactions occurs when the two interacting fragment orbitals have different symmetries and are unable overlap, (ie. a nodal plane is produced between the two molecules), otherwise they can only overlap antara-facially. This would require twisting of the dienophile' which is not possible in ethylene.[4]
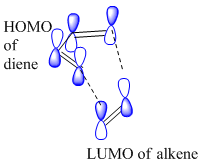
In Diel-Alder reactions, the diene is generally electron rich and the alkene is substituted, making it electron deficient. The formation of two σ provides a driving force for this reaction. Diels-Alder reactions involve the supra-facial overlap of the HOMO and LUMO of the reactants.The frontier orbital need to have the same symmetry for the reaction to be thermally allowed. Two Diels-Alder reaction will be analyzed in this part of the module. These are the reaction between butadiene and ethylene, and cyclohexa-1,3-diene and maleic anhydride. The transition states of these reactions will be optimized using the first method learned in the tutorial above; the frontier orbitals will also be visualized to observe how they help to explain the regiochemistry of the major product.
Figure 1b shows the typical supra-facial overlap of the frontier orbitals involved in a Diels-Alder reactions. The LUMO in the alkene is anti-symmetric with respect to plane of symmetry through the C=C bond. Also, the s-cis butadiene HOMO is anti-symmetric with reaspect to a plane of symmetry through the C(2) - C(3)single bond. Interaction of these orbitals are allowed.
Diels-Alder Reaction between Butadiene and ethylene
Using AM1 semi-empirical molecular orbital method, s-cis butadiene and ethylene were optimized separately. The log files for thesee calculations are DOI:10042/to-11382 and DOI:10042/to-11383 respectively. Butadiene HOMO and ethylene LUMO are antisymmetric with respect to the plane of symmetry shown in Fig. 2 as mentioned above. Meanwhile, butadiene LUMO and ethylene HOMO are symmetric with the same plane of symmetry. Reaction between diene LUMO and dienophile HOMO are possible when the alkene is electron rich and the diene is electron poor. This is an reverse electron demand system. However, the diene here is "electron rich" the HOMO of butadiene is expected to interact with the LUMO of ethylene. By examining the orbital interaction in the transition state this assumption can be confirmed.
 |
 |
 |
 |
Transition State Analysis
In order to optimize the transition structure of the Diels-Alder reaction. The AM1 optimized butadiene and ethylene were used to produce a guess transition state structure. The guess transition structure can be seen in figure 3. The double bonds in the reactants have been "delocalised", drawn as dashed bonds, because this would be expected in the transition state. The transition state was then optimised using AM1 semi-empirical method and optimization technique 2. This was repeated again using DFT/6-31g(d) level theory.
 |
| AM1 optimised Transition State DOI:10042/to-11451 | B3LYP/6-31G(d) optimised Transition State DOI:10042/to-11410 | |||||
|---|---|---|---|---|---|---|
| Energy /Hartree | 0.10745322 | -234.54390 | ||||
| RMS Gradient Norm/ Hartree | 0.00618695 | 0.00000594 | ||||
| Imaginary Frequency / cm-1 |  -419.28 -419.28 |
 -524.83 -524.83
| ||||
| Lowest Vibrational Frequency /cm-1 |  102.50 102.50 |
|||||
| The vibrations above show the approach of the carbon atoms on ethylene occurring one after the other. This would correspond to the formation of one bond and then the other rather than the concerted mechanism associated with Diels-Alder reactions. | ||||||
| Dipole / Debye | 0.4153 | 0.394 | ||||
| IR spectrum | 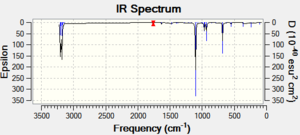 |
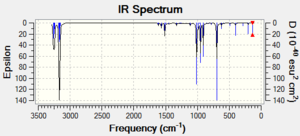
| ||||
| HOMO -1 |  Antisymmetric Antisymmetric
| |||||
| HOMO |  Antisymmetric Antisymmetric |
 Symmetric Symmetric
| ||||
| LUMO |  Symmetric Symmetric |
 symmetric symmetric
| ||||
| Geometry of Transition state |
| |||||
| C-C lit. Bond lengths/Å, | sp2-sp2= 1.38, sp3-sp3=1.46 Carbon van der waals radius = 1.70[5] | |||||
| Intrinsic Reaction Coordinate | 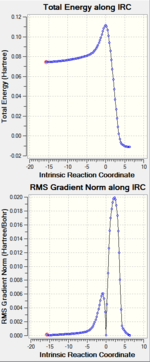 DOI:10042/to-11494 DOI:10042/to-11494 |
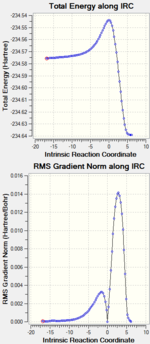 DOI:10042/to-11455 DOI:10042/to-11455
| ||||
| Both the IRC show the two possible routes for the transition state, to produce the produce or go back to the starting material. Nevertheless firstly, the structures above are confirmed to be the transition state because they are the highest energy structure in on these graphs. The reaction coordinate at zero correspond is the transition state and corresponds to the starting structure. Considering B3LYP/6-31G(d), as the reaction co-ordinate proceeds forward from zero towards 10, the product cyclohexene and the starting material, s-cis butadiene and ethylene, achieved are -234.63915000 and -234.57538828 Ha respectively. The energy of the product and starting material from the AM1 are 0.07458431 and -0.07099623 Ha respectively. | ||||||
The presence of a single imaginary frequency corresponding to the transition state, confirms successful optimization of the transition state. The HOMO orbital, when using the AM1 theory, shows clearly the symmetry expected for the supra-facial interaction of the HOMO and LUMO of butadiene and ethylene respectively - it is anti-symmetric, symmetry is preserved. The HOMO of the transition state, when using B3LYP/6-31G theory, at first appears strange because it shows a nodal plane between butadiene and ethylene. Nevertheless, corresponds to the allowed interaction of the butadiene LUMO and ethylene HOMO. As mentioned before, the orbitals here show the interaction of the LUMO of butadiene and HOMO of ethylene, this molecular orbital is symmetric around the plane of symmetry cutting through the C(2)-C(3) bond in butadiene and C=C in ethylene.
The bond lengths in the AM1 optimized transition structure are generally suggest that the reaction is further along in the B3LYP/6-31G(d) than in AM1. The C=C bond in butadiene in AM1 is shorter than in B3LYP/6-31G(d), meanwhile the C(2)-C(3) bond in butadiene is longer in Am1 than in B3LYP/6-31G(d). However the distance between the fragments in greater in B3LYP/6-31G(d) than inAm1. The distance between the two fragments is less than double the carbon Van der waals radius, ergo there is a fair amount of overlap between the orbitals already in the transition state.
Diels-Alder Reaction between Maleic Anhydride and 1,3-Cyclohexadiene
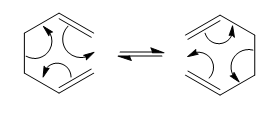
Maleic anhydride reacts with 1,3-cyclohexadiene via a Diels-Alder reaction to give two possible products. The kinetic, endo product, is generally the major product whilst the exo-product is produced as the major product under forcing conditions. By analysing the molecular orbitals of the transition state the secondary-orbital interaction, responsible for making the endo product the major product, can be identified. In this Diels-Alder reaction the endo product is also the thermodynamic product.
The endo product is produced when maleic anhydride approaches the diene with the anhydride part of the molecule underneath 1,3-cyclohexadiene. This allows for favourable secondary-orbital interaction which lowers the energy of the transition state, hence the reactions follows that lower pathway.
 |
The transition state for the reaction above was optimised to a TS(BERNY) using B3LYP/6-31G(d) level theory, endoDOI:10042/to-11445 and exo DOI:10042/to-11446 . The molecular orbitals of the reactants can be found in table 2.
| Maleic Anhydride B3LYP/6-31G(d) DOI:10042/to-11456 | 1,3-Cyclohexadiene DOI:10042/to-11457 | ||||
 |
 |
 |
 |
 |
 |
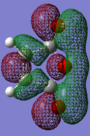
Superior method B3LYP/6-31G(d) has produce molecular orbitals with correspond with expectation for maleic anhydride. Naturally, the p-orbitals on oxygen should be in the HOMO of the molecule. Such thorough calculation enables quick recognition of the orbital interacting this Diels-alder reaction, for example LUMO of maleic anhydride is overlapping with the HOMO of 1,3-cyclohexadiene to make the HOMO in the exo and endo transition state.
Molecular orbitals with the same symmetry with respect to the same plane of symmetry will have favorable interactions. Maleic anhydride HOMO and 1,3-cyclohexadiene LUMO interaction is allowed whilst interaction of maleic anhydride LUMO and HOMO of 1,3-cyclohexadiene is allowed.
The anhydride group of maleic anhydride is electron withdrawing making the double bond electron deficient. Meanwhile cyclohexadiene is electron rich, as the alkyl electrons are electron donating. Subsequently the LUMO of maleic anhydride and 1,3-cyclohexdiene will be expected to be the dominating interaction in the transition state of this Diels-Alder reaction.
The molecular orbitals of the endo and exo transition state can be found in the table below.
| HOMO-1 | HOMO | LUMO | LUMO+1 | ||
|---|---|---|---|---|---|
| Endo |  |
 |
 |
 | |
| Exo |  |
 |
 |
 | |
This most significant different in the bond lengths of the endo and exo transition state is that maleic anhydride is closer to 1,3-cyclohexadiene in the edno transition structure than the exo.
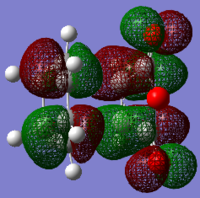
Secondary orbital interactions can clearly be seen in the LUMO+1 orbital of the endo transition state. The C=O π orbital is interacting with the maleic anhydride C=C π orbitals. The orbitals in the endo LUMO-1 is more condensed than in the exo. These close interaction, although it is in the LUMO+1, are stabilizing the transition state of the endo molecule. The HOMO and LUMO of the exo and endo are equal except for the LUMO-1, ergo it is this orbital interaction which is responsible for the preference of the endo, kinetic product over the exo thermodynamic product.
Intrinsic Reaction Co-ordinate
| Endo IRC | Exo IRC | ||||
|---|---|---|---|---|---|
 |
 | ||||
| DOI:10042/to-11513 | DOI:10042/to-11518 | ||||
The IRC confirm that the transition state was indeed optimized since it the structure with the highest energy on the graph.
Conclusion
Through this exercise, it has been demonstrated that the endo transition state lower in energy than the exo. DFT-B3LYP/6-31g(d) theory level optimization of the transition and visualization of the molecular orbitals helped to identify the secondary orbital interaction which is stabilizing the endo transition state. It has also been shown that the endo product is the thermodynamic product. The effectiveness of the different calculation levels have also been examined, and of course the DFT-B3LYP/6-31g(d) has proved itself superior in the exercise.
In conclusion this course has added an extra dimension to chemistry, allowing students to visualized concepts, eg. secondary orbital interaction, that mentioned and maybe taken for granted. It is obvious that the secondary orbital interaction is in the LUMO+1 orbital in the transition state. It is also interesting to actually to calculate the the IRC to observe the transient transition state and the vibrational frequencies associated with the that reaction step.
- ↑ M. J. Goldstein, M. S. Benzon, J. Am. Chem. Soc., 1972, 94 (20), pp 7147–714, Template:DOI: 10.1021/ja00775a046
- ↑ Rsults Table in Module 3 wiki page, wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:phys3, date:16/12/11
- ↑ Olaf Wiest, Kersey A. Black, and K. N. Houk', J. Am. Chem. SOC., Vol. 116, No. 22, 1994 10337
- ↑ Henery Rzepa, Pericyclic Reaction Course, Imperial College London,http://www.ch.ic.ac.uk/local/organic/pericyclic/, date:16/12/11
- ↑ Bondi, A. J. Phys. Chem., 1964, 68',3 pg.441–51. DOI:10.1021/j100785a001 .