Rep:Mod:RUNAOns1

Module 1: Organic

Modelling Using Molecular Mechanics

Molecular mechanics computes the energy of a molecule in terms of a set of classical potential energy functions.

The potential energy functions and the parameters used for their evaluation are known as a “force-field”. Molecular Mechanic methods are based on the following principles:

• Nuclei and electrons are lumped together and treated as unified atoms
• The atoms are treated as spheres and bonds are treated as springs
• Non-bonded interactions between atoms are described using potential functions derived from classical mechanics
• Individual potential functions are used to describe the different interaction
  • eg. bonding stretching,angle bending, torsion (bond twisting), and through space interactions
• Potential energy functions rely on empirically derived parameters (force constants, equilibrium values) that describe interactions between sets of atoms
• The sum of the interactions determines the conformation of the molecule
• Molecular mechanical energies are only have meaning when used to compare relative steric energy between two or more conformational isomers of the same molecule

After an energy minimization calculation, the total energy of the molecule is given as a summation of the additive, non-interacting terms below.

Stretch - represents the energy associated with distorting bonds from their optimal length. It is comprised of diatomic bond stretches each expressed as a simple Hookes law potential

Bend - is the energy associated with deforming triatomic bond angles from their optimal values (also a simple Hookes law potential)

Stretch-Bend - represents the energy required to stretch the two bonds involved in a bond angle when that bond angle is severely compressed.

Torsion - represents the energy associated with tetra-atomic bond torsions (a cosine dependance)

Non-1,4 van der Waals - term represents the energy for the through space interaction between pairs of atoms that are separated by more than three atoms.

1,4 van der Waals - is the energy of the through space interaction of atoms separated by two atoms.

Dipole/Dipole - represents the energy associated with the interaction with the interaction of bond dipoles.

Cyclopentadiene Dimer

Cyclopentadiene dimerises readily at room temperature via a Diels-Alder reaction to give two possible isomers. The Endo Rule suggests that the kinetic endo product will be the major product in the reaction under non-thermodynamic conditions. Using computational chemistry, MM2 force field, to calculate the total energy of the exo and endo cyclopentadiene dimer isomers, the thermodynamic product can be determined.

Structure 1: The exo-dimer of cyclopentadiene

Structure 2: The endo-dimer of cyclopentadiene

Table 1:Energies of the exo and endo isomers of cyclopentadiene dimer calculated using Allinger's MM2 force field.

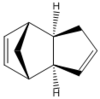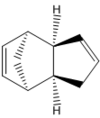	Energies/ kJmol-1
	Stretch	Bend	Stretch-Bend	Torsion	Non-1,4 VDW	1,4 VDW	Dipole-Dipole	Total Energy
exo structure 1	5.38	86.11	-3.51	32.04	-5.93	17.72	1.58	133.37
endo structure 2	5.23	87.22	-3.50	39.79	-6.45	18.07	1.87	142.25

Fig. 1a: 'Structure of the exo showing possible reasons for the reduced torsion and bend energy of the molecule. Fig. 1b: Structure of the endo-dimer of cyclopentadiene illustrating the distance responsible for the increase torsion energy in this product.

Clearly the exo product is thermodynamically favored because its total energy is approximately 9 kJmol^-1 lower then endo product's total energy. In both molecules, stretch-bend and non-1,4 van der Waals energies are stabilizing the molecules. However the torsion energy of the endo product is the major term increasing the total energy of the isomer. From examining the Jmol structures the tetra-atomic arrangement responsible for the increase in the torsion can be observed, these structure have been shown more clearly in in fig. 1. All the angle strains results in the endo product having a larger bend energy, for example there is a larger deviation of angle between C(7), C(8) and C(4) from 109^o in the endo product compared to the exo. The tetra-atomic bond torsion mostly responsible for the endo product being the non-thermodynamic product have been highlighted in Fig. 1b. There are two of these interactions in the molecule due to the plane of symmetry in the cylohexene ring part of the molecule. In comparison, there is a larger distance similar atoms in the exo product supporting the fact that is the thermodynamic product.

Molecular mechanics tells chemists the most thermodynamic product. From this information, though, the major product in the dimerisation reaction of cyclopentadiene can not be determined. However by looking at the cyclopentadiene dimerisation mechanism and identifying the secondary orbital interaction in the formation of the endo product, it can be concluded that the endo product is the kinetic product.It's transition state is more stabilised, and thus provides a lower energy pathway, than that of the exo product. Consequently, the endo product would be the major product in the dimerisation of cyclopentadiene. Under kinetic control, dimerisation of cyclopentadiene is irreversible, consequently the lower energy pathway is taken and thus the major product would be the endo isomer.

Structure 3: The hydrogenated cyclopentadiene

Structure 4: The hydrogenated cyclopentadiene

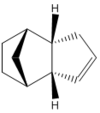The Hydrogenation of endo-Cyclopentadiene Dimer

The endo-cyclopentadiene dimer can be hydrogenated to give a dihydro structure, under forcing conditions the tetrahydro derivative is obtained. By calculating the energies of the two isomers, the thermodynamically favored product can be determined. Again, this information does not confirm the experimental major product. Information on the transition state of molecule during hydrogenation is needed to identify the product with the lower transition state. It is of course possible that the thermodynamic product is also the kinetic product, however modeling the transition states these molecules during hydrogenation is required to ascertain the the major product of the reaction.

Table 2: Energies of the endo-hydrogenated cyclopentadiene dimer isomers.

	Energies/ kJmol-1
	Stretch	Bend	Stretch-Bend	Torsion	Non-1,4 VDW	1,4 VDW	Dipole-Dipole	Total Energy
Structure 3	5.23	80.15	-3.50	46.34	-6.88	24.26	0.68	146.29
Structure 4	4.59	60.78	-2.30	52.29	-4.48	18.88	0.59	130.34

Structure 4 is the thermodynamic dihydro derivative of the endo-cyclopentadiene product because its energy is 16 kJmol^-1 lower than the total energy of structure 3. A number of factors are increases the molecular energy of structure 3, namely the bending energy, torsional strain and 1,4 van der Waals interaction. The large bend engergy in structure 3 is due to the small angle (108^o compared to the expected 120^o) between the alkene double bond and the adjacent single bond. This angle has been highlighted in fig. 2a. The corresponding angle in structure 4 is 112^o, this supports structure 4 having a lower angular strain.

Figure 2a and 2b: Jmol of structure 3 and 4 from left to right.
Structure 3	Structure 4

Overall the use of molecular mechanics to identify thermodynamic products in a reaction have been utilized. However, it has been recognized that more information, such as reaction mechanisms and transition state energy are required in order to make substantial predictions on the outcomes of reactions.

Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

An intermediate used in the synthesis of taxol, structure 5 or 6, is initially prepared with the carbonyl group pointing either up or down. These are atropisomers, the rotation around a single bond is large enough to allow these structures to be isolated as conformers.. Structures 5 and 6 were minimized using MM2 and MMFF94 for comparison. The conformational isomers of the taxol intermediate are illustrated in structures 5 and 6 and the energies of these structures have been tabulated in table 3.

Structure 5: The taxol intermediate molecular structure where the carbonyl is up.

Structure 6: The taxol intermediate molecular structure where the carbonyl is down.

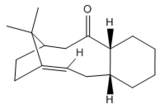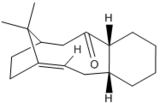Structure 6 is more thermodynamically stable than 5, as shown in table 3. The most stabilizing contribution to the overall energy, for both conformations, is the non-1,4 van der waals interactions due to the interaction of the carbonyl oxygen with neighbouring hydrogen atoms. The non-1,4 van der Waals interaction is greatest for structure 6, possibly due to the closer proximity of hydrogen atoms to the carbonyl oxygen when the carbonyl group is facing down. Bend, torsion and non-1,4 van der Waals interaction are the more destabilizing interaction in structures 5 and 6. The bridging group is increasing the energy of the molecule. Nevertheless, in structure 5 where the carbonyl group is up resulting in increased angle strain, along with the bridging group on the molecule a the larger bend and torsion energy is observed. From angles highlighted in Jmol structures 5 and 6, it can be recognised that the angles in structure 5 have deviated more from ideal that those in structure 6, ergo resulting in a higher bend energy.

Table 3: The lowest energies of structure 5 and 6 isomers minimised using MM2.

	Energies/ kJmol-1
	Stretch	Bend	Stretch-Bend	Torsion	Non-1,4 VDW	1,4 VDW	Dipole-Dipole	Total Energy
Structure 5	11.18	66.56	1.67	76.40	-4.92	53.08	0.61	205.57
Structure 6	10.58	44.56	1.33	82.78	-5.77	52.52	-0.75	185.27

Structures 5 and 6 can be seen as three fused cyclohexane rings. The first ring and second rings conformations are relatively tightly locked because of the bridging group. Consequently, the first nearly always has an eclipsed boat-like conformation, which would destabilize the molecule. In structure 6, since the carbonyl group is facing down there is less eclipsed structure than in structure 5. All these factors contribute to make structure 6 the more thermodynamicaly stable conformer.

A number of conformations are possible for structures 5 and 6, by changing the conformation of the cyclohexyl ring. The total energies of these structures have been collated in the table below. Structure 5a gives the taxol intermediate 5 in its most stable conformations because the cycloheyl ring is in a chair conformation and the whole molecule is a staggered as possible. Structure 5b has the cyclohexyl group in a twist boat conformation, since this is an energy maximum in a energy profile of cyclohexane the conformation produces a high energy conformer in the intermediate. Similarly this have be observed in structure 6c which has molecular energy that is nearly three times its chair alternative (structure 6 a). Meanwhile, structure 6b also refers to the chair conformation of the cycloheyl ring, but the up position of the carbon circled in fig. 3 is increasing the energy of the system.

Table 4: The energies of different conformation of structures 5 and 6.

	Total Energy
	MM2/ kcal mol-1	MMFF94/ kcal mol-1
Structure 5a (Chair)	204.60	295.14
Structure 5b	469.09	319.26
Structure 6a (Chair)	185.28	253.38
Structure 6b	222.61	312.85
Structure 6c (Twist boat)	533.29	277.55

Fig. 3: Comparison of structure 6a and 6b.

The geometry of conformers have been minimised using MM2 and MMFF94. These produce energy values that are very different in size, however, the same trends trends in energy persist in the two sets of data. Although it must be recognised that the difference in MM2 calculated energies for the structures tend to be higher that than that from MMFF94 calculation.

Experimentally it is found that electrophiic additions to the double bond in both structuresis slow. This reactivity is expected when considering the rehybridisation required (sp² to sp³) in such a reaction and the diasterous consequence this would have on angle strain. Consequently, these taxol intermediate are hyperstable alkenes because they are more stable than their corresponding alkane.

Modelling Using Semi-empirical Molecular Orbital Theory.

Regioselective Addition of Dichlorocarbene

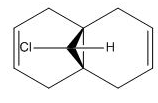
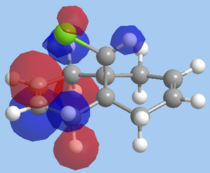
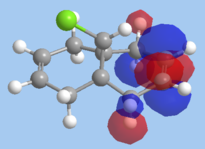
Molecular mechanics will be used to assess the the reactivity of double bonds in structure 7. The structure was first minimised using MM2 and then MOPAC using PM6 method, the HOMO and LUMO orbitals of dichlorocarbene were calculated using MOPAC/PM6 and RMI. Orbitals obtained from RMI were more symmetric than those from PM6, for that reason the molecular orbital surfaces from RMI calculation is used in this report. The optimization file can be found on DOI:10042/to-10371

Structure 7

Fig. 6: Reaction of dichlorocarbene with Molecular structure of dichlorocarbene.

Structure 7: HOMO - 1

Structure 7: HOMO

Structure 7: LUMO

Structure 7: LUMO +1

Structure 7: LUMO +2

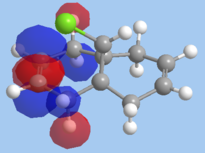On the whole, the orbitals from MOPAC/RMI are fairly symmetrical with respect to the plane of symmetry in this C_s molecule. The molecular orbitals obtained are in line with chemistry intution. A π-orbital is expected to be the HOMO orbitals. However the position of the Cl atom is affecting the energy of the endo π-orbital. The difference in energy of the two double bonds is due interaction of the exo π-orbital with Cl-C σ* orbital. Energy of the exo π-orbital is therefore lowered as shown in the molecular diagram in fig. 7. Reason for regioselective addition to the endo π-bond can now to explained. The endo π-bond is the more nucleophilic than the exo since it is at a higher energy. Therefore, electrophilc addition reaction wil occur at the endo π-bond first.

Fig. 7: Molecular orbita diagram to show the lowever of the exo π-orbital

Vibrational Energy

PM6 was used to optimise the geometry of dichlorocarbene, and Guassian interface was used to create a B3LYP/6-31G(d,p)input file used by SCAN to measure the optimum vibrational frequency of the molecule. The vibrational energy measured and the group stretches responsible for them have been tabulated below.

Bond	Structure 7		Dihydro derivate of Structure 7
	Calculated Bond Length/Å	Wavenumber of stretch/cm-1	Calculated Bond Length/Å	Wavenumber of stretch /cm-1
C-Cl	1.789	772.59	1.791	776.84
C=C endo	1.332	1760.98	1.332	1761.67
C=C exo	1.336	1740.81	-	-

These calculated vibrational frequencies agree with the arguement put forward above. Cl-C vibration in structure 8 occurs at a sligthly lower wavenumber because as electron density from the exo double bond to the Cl-C σ*orbital weakens the Cl-C σ bond. Following this, the exo C=C bond vibration is lower than the endo vibration because the bond is losing electron densit to the Cl-C σ* orbital. There is little change in the calculated bond lengths between the two structures. Furthermore the Cl-C bond length in structure 8 is shorter than in structure 9 due to weakening of the bond by the pi-donation into its σ* orbital.

Monosaccharide chemistry: glycosidation

[[File:AnomerA_MM2.png|structure of anomer A with the carbonyl below the plan of the oxonium ion]

anomer a

anomer b

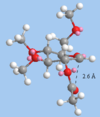MM2 states that the energy of anomer a (29.70 kJmol^-1) is higher than that of anomer b. In anomer a, the carbonyl is further away from the delta positive oxonium carbon than in anomer b. This interaction therefore stabilises the structure of b more than a.

Mini-Project: Assigning regioisomers in "Click Chemistry"

Click chemistry, introduced by Sharpless, is an umberella term used to describe a range of chemical reactions with certain desirable properties. Such properties include; simple reaction conditions, stereospecificity in reactions, high yield and atom economy,and preparation of simple products with non-offensive byproducts being generated.

1,3-Dipolar cyloaddtion between azide and an alkyne is a click reaction. This reaction, also known as the azide Huisgen alkyne cyloaddition, proceeds via an aromatic transitions state to give a 1,4-disubstituted triazole with a copper (II) catalyst. In the presences of ruthenium catalyst the 1,5-disubstitute product is obtained.

However this project aims to use the computational skills gained whilst completing module 1 to confirm which regioisomer is produced when Cu(II) catalyst is used. C¹³ NMR will be calculated and compared with the experimental results obtained by Zhang et. al.

Mechanism of 1,3-dipolar cycloaddition

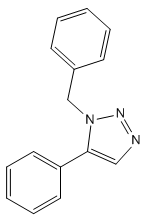
There are three aromatic-pi systems in these molecule. Therefore the molecules are expected to be highly planar in order to maximise the overlap integral between the cyclic p-orbitals. This is mostly the case, but due to the methylene group on the azide the structure is not fully planar as shown in the Jmol structures.

Energy minimisation using MM2 force field suggests that the 1,4-product is the thermodynamic product it has energy 10.67 kJmol^-1 whilst the 1,5-product has 17.24 kJmol^-1. It is the angluar strain which increases the bend energy of the 1,5-product making it in the less favoured regioisomer. The angle responsible for this have been highlighted in the Jmol structure.

Structure 9: 1,4-product

Structure 10: 1,5_product

Assignment of the C¹³ NMR of the regioisomers.

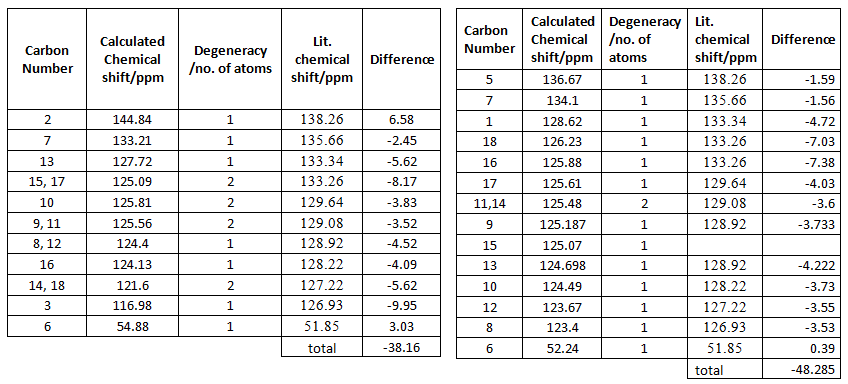
The table of the NMR data can be found below. There are more peaks in the calculated NMR than in the experimental. Eleven peaks should be expected becasue there are four pairs of equivalent carbon atoms in the structures. Phenomena, such as spin-orbit coupling may be limiting the ability SCAN to relistically calculate the NMR, especially since there is a lot of aromatic ring systems in the products.

All the carbon appeared in the expected region for aromatic carbon, approximately 100 - 150 ppm. The most shielded carbon is the methylene carbon. This is because it is the perfect distance away from the hetroaromic ring to experience the shielding effect of the ring current. On the other hand carbon 2 inthe 1,4 product and carbon 5 in the 1,5 product are the most deshielded carbons because the phenyl group is withdrawing electron density from the heteroaromatic ring and furthermore nitrogen also withdraw electron density due to its electronegativity.

From the table, the overall difference in the NMR data suggest that the 1,4-product is the most likely product because it has the smalles deviation from literature.

Structure 10: 1,4-product

Structure 11: 1,5_product

Structure 10: 1,4-product, C13 NMR assignment for the 1,4 and 1,5 product respectively.

Conclusion

Admittedly there is much scope for improvement on this report, due to time limitations, further analysis and such as proton NMR and more literature references could be used to analyze the data fully. Nevertheless, this project has demonstrated the a variety of equipment and software chemists have at their disposal to to analyze and elucidate the structures of compounds and access stereo and regioselectivity. Having said this though, computational chemistry can not be independent of theoretical and practical chemistry as demonstrated by the exercise on the dimierizsation of cyclopentadiene and its hydrogenation. Questions raised in these exercises required practical work and chemical intuition to be solved, and were not easily answered by computational chemistry. Also, limitations in computational chemistry to deal with animated dynamic molecules in the mini project had resulted in poor matching between calculated chemical shifts and literature. In fact, the equivalency of atoms appears to be quiet random when looking at the computational NMR data. Alternatively an NMR spectrum of the sample could have confirmed the regioisomer quite easily.