Rep:Mod:RS5215
NH3 Molecule
NH3 Molecule |
Optimization Summary
Below is a table containing a summary of how the optimization was calculated and a few physical properties.
| Molecule | NH3 |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| E(RB3LYP) /a.u. | -56.55776873 |
| RMS Gradient /a.u. | 0.00000485 |
| Point Group | C3v |
| Optimized N-H Bond Length | 1.01798 |
| Optimized H-N-H Bong Angle | 105.741o |
This is the 'Item' table which shows that the optimization has completed and has really converged onto a stationary point.
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
A link to the completed NH3 optimisation file can be found here.
Vibrational Analysis
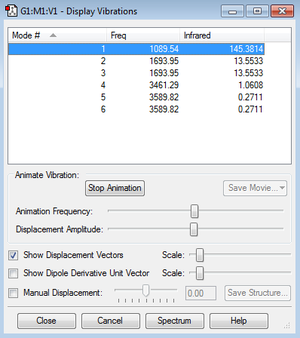
Using the 3N-6 rule, 6 modes are expected as N is equal to 4. The screenshot shows that this expectation is confirmed.
Modes 2 and 3 are degenerate as well as modes 5 and 6. Modes 1-3 are "bending" vibrations and modes 4-6 are "bond stretch" vibrations. Mode 4 is highly symmetric.
Mode 1 is known as the umbrella mode.
In an experimental spectrum of gaseous ammonia, you would expect to see 4 bands in the spectrum as the degenerate modes would result in a single band.
Charge Analysis
A negative charge would be expected on the nitrogen atom as it is highly electronegative; as a result the hydrogen would be expected to have a positive charge.
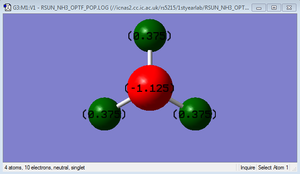
As expected, the charge on the nitrogen atom is -1.125 and the charge on each hydrogen atom is 0.375.
H2 Molecule
| Molecule | H2 |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| E(RB3LYP) /a.u. | -1.17853936 |
| RMS Gradient /a.u. | 0.00000017 |
| Point Group | D∞h |
| Optimized H-H Bond Length | 0.74279 |
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES
There is one mode of vibration with a frequency of 4465.68.
N2 Molecule
| Molecule | N2 |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| E(RB3LYP) /a.u. | -109.52412868 |
| RMS Gradient /a.u. | 0.00000060 |
| Point Group | D∞h |
| Optimized N-N Bond Length | 1.10550 |
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
N2 also has one mode of vibration with a frequency of 2457.33
Molecular Orbitals
Nitrogen has an electronic configuration of 1s22s22p3 and so N2 has 7 occupied molecular orbitals (MOs).
The following are images of the bonding and antibonding MOs produced by the 1s atomic orbitals (AOs).
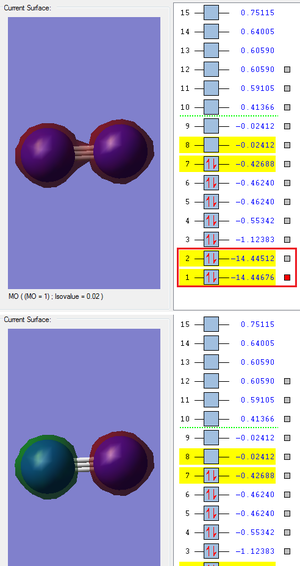
The highlighted band shows the energies of both the MOs. They are much deeper in energy than the MOs produced by the valence AOs. They are also not very involved in chemical bonding as there is hardly any overlap between them. The difference between their energies is not very great which is also due to the lack of overlap.
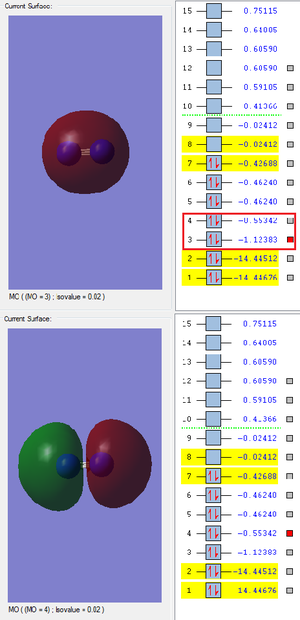
The next band is the MOs produced by the 2s AOs. As these are valence AOs there is a much greater overlap and they are heavily involved in the chemical bonding. There is also a greater difference in the energy of the bonding and antibonding MO which is due to intensity of the overlap.
Reaction Energies
Using the energies of the molecules above, the energy of the reaction 3H2 + N2 -> 2NH3 can be found. All following energies are in atomic units.
E(NH3)= -56.55776873
2*E(NH3)= -113.11553746
E(N2)= -109.52412868
E(H2)= -1.17853936
3*E(H2)= -3.53561808
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -113.11553746 - [-109.52412868 + -3.53561808]
= -113.11553746 - -113.05974676
ΔE = -0.0557907
After converting to kJ per mole the result is -146.47848285 kJmol-1.
As the reaction is exothermic, the product would be lower in energy than the reactants are. Therefore, the product is more stable than the reactants.
Project Molecule: Cl2
Optimization Summary
| Molecule | Cl2 |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| E(RB3LYP) /a.u. | -920.34987886 |
| RMS Gradient /a.u. | 0.00002510 |
| Point Group | D*H |
| Optimized Cl-Cl Bond Length | 2.04174 |
| Optimized Cl-Cl Bong Angle | 180o |
Item Value Threshold Converged? Maximum Force 0.000043 0.000450 YES RMS Force 0.000043 0.000300 YES Maximum Displacement 0.000121 0.001800 YES RMS Displacement 0.000172 0.001200 YES
Vibrational Analysis
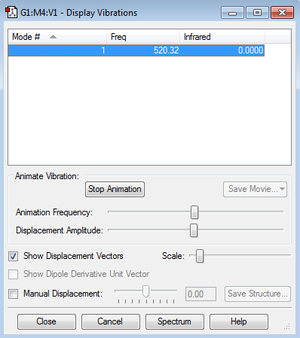
The screenshot shows that there is only one mode of vibration, as expected from the 3N-5 rule for linear molecules. The vibration is a 'bond stretch' vibration.
Charge Analysis
It is expected that both atoms in Cl2 have a charge of zero as it is a homonuclear diatomic molecule and so both atoms have the exact same electronegativity.
Molecular Orbitals
The electronic configuration of a chlorine atom is 1s22s22p63s23p5, hence in Cl2 17 occupied molecular orbitals are expected.
Below are images of a few molecular orbitals followed by a description of each.
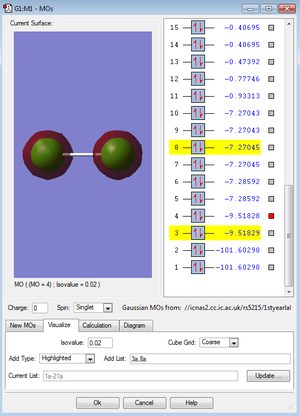
At -9.5, these are deeper in energy than the MOs produced by the valence electrons, however they are not as deep in energy as the molecular orbitals formed by the 1s2 atomic orbitals. The 1s2 AOs combine to form molecular orbitals that are incredibly deep in energy - at around -101.6.
For both the 1s and 2s MOs there is barely any overlap at all and the AOs are tightly constricted to their respective nuclei.
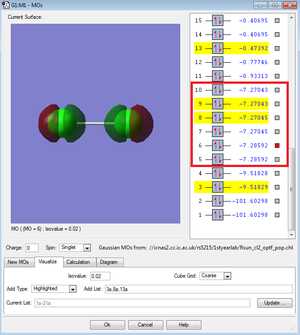
The red box highlights the MOs formed by the 2p AOs.
These MOs are also deeper in energy than the MOs produced by the valence electrons - these are in the range of -7.2 to -7.3. Similarly to the 1s and 2s orbitals, there is no overlap. Because of this, the difference in energy between the bonding and antibonding MOs is very slight. These orbitals are not very involved in chemical bonding.
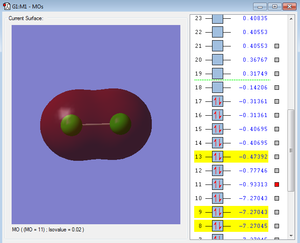
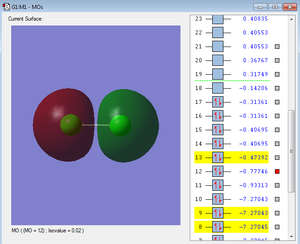
These are formed by the valence AOs. They have a much more extensive overlap and are heavily involved in chemical bonding. Dissimilar to the bonding and antibonding MOs of the inner AOs, the difference of energy between the 3s bonding and antibonding MOs is greater due to the strong overlap of the bonding MO.
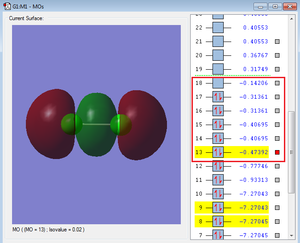
The red box highlights the MOs formed by the 3p AOs. The bonding MO shown above has a very strong overlap and a higher energy than the 2p MOs. These are also heavily involved in chemical bonding. Similarly to the 3s energies, the range of energies of the 3p MOs is greater than the range of energies of the MOs produced by the 2p AOs, also due to the much stronger overlaps.
MOs 16 and 17 are the HOMOs (which are degenerate 3p antibonding MOs) and MO 18 is the LUMO (which is also a 3p antibonding MO from the along bond).

