Rep:Mod:RP2513

Introduction

This computational experiment is centred on characterising transition structures for two types of reactions, the Cope-rearrangement and the Diels-Alder reaction. For the Cope-rearrangement, focus is put on the optimisation of the chair and boat transition structures of the [3,3] sigmatropic rearrangement of 1,5-hexadiene. The Diels Alder reaction study is based on the transition structure of the [4+2] cycloaddition of ethene and butadiene. The cycloaddition reaction of maleic anhydride and cyclohexa-1,3-diene is also discussed, with the exo and endo transition states being investigated.

Transition states correspond the the energy maxima on a potential energy surface and thus cannot normally be isolated as they fall back to the minima of the reactants and products. Nevertheless, computational chemistry allows for the study of these transition states. The analysis of transition states allow for key information on the reaction to be found such as the activation energy and the reaction mechanism.

This study uses the Gaussview programme to draw the reactants and form the transition states, while optimising them with various level of theory. The calculation methods used for these optimisations are Hartree-Fock/3-21G, B3LYP/6-31G(d) and Semi-Empirical/AM1 levels of theory.

The Cope rearrangment of 1,5-hexadiene

Background

The Cope rearrangement is a pericyclic reaction involving the [3,3] sigmatropic rearrangement of 1,5 dienes. It was first discovered by Arthur C. Cope in 1940, and has since been used extensively in organic synthesis. The Woodward-Hoffman rules can be applied to this reaction and show it is thermally allowed. This is because the Cope rearrangement consists of a suprafacial component (σ2_s) and 2 antrafacial components (π2_a), which when applied to the equation (4q + 2)_s + (4r)_a gives an odd number, confirming it is thermally allowed. This study focuses on the Cope rearrangement of 1,5-hexadiene, as shown in the reaction scheme in figure 1.

The Cope rearrangement has undergone a number of experimental and computational studies, with particularly focus on its mechanism. In the past there has been disagreement on whether the reaction occurs via a concerted mechanism or not. However, it is now accepted that it occurs through a concerted mechanism through a boat or chair transition structure. In this study the reactants, products and transition states have been investigated. The calculations for these studies were performed using the Density Functional Theory and Hartree-Fock levels of theory.

Figure 1. The Cope Rearrangement of 1,5-hexadiene.

Nf710 (talk) 13:38, 10 February 2016 (UTC) Good Mechanistic understanding on the reaction.

Comparison of Hartree-Fock and Density Function Theory

The calculations in this study are focused on finding the local minima of the products and reactants and the maximum associated with the transition state. The Density Functional Theory and Hartree-Fock levels of theory are used to do this. The HF level of theory approximates the wavefunctions using the Slater determinant. DFT looks at functionals of electron density rather than at wavefunctions. HF theory finds the energy of the electrons in molecular orbitals by using a mean field for electron interactions, ignoring electron correlation. HF doesn’t account for the electron correlation because electrons of the same spin can be placed together in a orbital which is not allowed and would cause the calculation to be incorrect. This causes values calculated using HF theory to be higher than the true value. DFT produces more accurate results and values that are more precise, this is because it uses less approximations than HF and accounts for electron correlation.

Nf710 (talk) 13:52, 10 February 2016 (UTC) Method based on HF (with the appropriate corrections) are actually more accurate. But yes you are correct that because the probability in space of electrons with opposite is not correlated (they can be at the same place at the same time) the the colombic repulsion is higher and therefor you can a slight error in the energy.

Optimisation of the Conformers of 1,5-Hexadiene

To start, several conformers of 1,5-hexadiene were drawn in Gaussview and were optimised using the HF/3-21G level of theory, the results for this can be seen below.

Conformer	Jmol Structure	Energy (Hartrees)	Point Group	Summary of Results
anti2		-231.69253528	Ci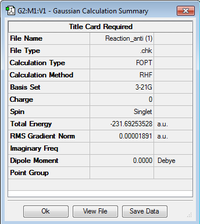
gauche3		-231.69266120	C1
gauche6		-231.68916020	C1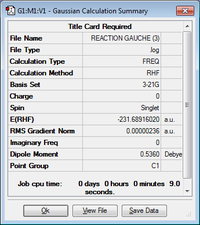

The lowest energy conformer for 1,5-hexadiene was found to be the gauche3 conformer. Initial expectations may be that it has more steric clash than other conformers and would be higher in energy. However, by looking at the molecular orbitals it can be seen that the twist in the structure allows for secondary orbital interactions between the π bonds, with favourable inphase overlap of the orbitals in the π system, this is shown in figure 2.

Nf710 (talk) 13:54, 10 February 2016 (UTC) Good use of the orbitals to expalin the energy differences

Figure 2. MO showing favourable interactions in gauche3.

Reoptimisation of the Anti2 Conformer of 1,5-Hexadiene at B3LYP/6-31G(d) Level of Theory

The anti2 conformer was reoptimised at the B3LYP/6-31G(d) level of theory, the results are shown below.

Conformer	Jmol Structure	Energy (Hartrees)	Point Group	Summary of Results
anti2		-234.61171061	Ci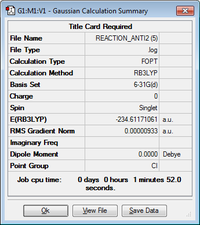

The energies of the two different levels of theory cannot strictly be compared as different approximations are used. However, it can be seen that as discussed earlier, the Hartree-Fock method gives an energy that is higher than for the Density functional theory. This is because DFT takes in account the electron correlation due to spin and charge, whilst HF does not which causes it to have a higher energy. Although the energies cannot be directly compared, the difference in geometries can be compared and discussed.

Nf710 (talk) 14:22, 10 February 2016 (UTC) Good explanation. they have different hamaltonians

Atoms	HF/3-21G (Å)	B3YLP/6-31G(d) (Å)
C14-C12	1.31613	1.33349
C12-C4	1.50891	1.50423
C4-C1	1.55275	1.54811

It can be seen when comparing the two levels of theory that for HF/3-21G the C14-C12 bond length (C=C) is shorter, while for C12-C4 and C4-C1 the bond lengths are longer. The literature values for these are (C14-C12: 1.34 Å, C12-C4: 1.51 Å, C4-C1: 1.54 Å). Comparing these to the values found it can be seen for the C14-C12 bond length the DFT method is closer to the literature value while for C12-C4 and C4-C1 both levels of theory are close. This shows that the B3LYP/6-31G(d) level theory is better at producing the structure.

Atoms	HF/3-21G (°)	B3YLP/6-31G(d) (°)
C14-C12-C4-C1	114.66877	118.57123
C12-C4-C1-C10	180.00000	180.00000
C4-C1-C10-C7	-114.66877	-118.57123

The dihedral angles of the two conformers are shown in the table above. It can be seen that the DFT method gives a value for the dihedral angle that is approximately 4° higher than the HF method. The DFT method gives a value of dihedral angle closer to 120° which is the expected value for an sp2 hybridised carbon which is trigonal planar.

Nf710 (talk) 14:25, 10 February 2016 (UTC) dihedral is not to do with hybridisation that would be a 3 center bond angle which is 120 for sp2.

Frequency Analysis

Frequency analysis was performed on the B3LYP/6-31G(d) optimised anti2 structure, the results can be seen below.

Figure 4. Summary of the anti2 conformer frequency analysis.

Figure 5. IR spectrum of the anti2 conformer, obtained using a frequency analysis.

The vibrational frequencies are shown in the IR spectra below. It can be seen all values are positive and real and show no negative imaginary frequencies. Imaginary frequencies are found at the maxima on a potential energy surface, while at a minimum only real positive values are found. This is because imaginary frequencies represent a negative in the second derivative of the potential energy surface thus represent a maximum which is the transition state. The second derivative of energy is the force constant for the degree of freedom, at a maxima the derivative will be negative thus the force constant will be negative. From the equation below it can be seen that from the square root of the negative force constant an imaginary solution will be formed and thus an imaginary frequency. A positive second derivative represents a minimum and gives positive vibrations which is what was observed here.

$v=\frac{1}{2\pi }\sqrt{\frac{k}{m}}$

A number of thermochemical values were calculated from the frequency analysis, this can be seen below.

	0K	298K	500k	1000k
Sum of Electronic and Zero-Point Energies (Hartrees)	-234.469214	-234.469214	-234.469214	-234.469214
Sum of Electronic and Thermal Energies (Hartrees)	-234.469214	-234.461866	-234.451158	-234.408594
Sum of Electronic and Thermal Enthalpies (Hartrees)	-234.469214	-234.460922	-234.449575	-234.405427
Sum of Electronic and Thermal Free Energies (Hartrees)	-234.469214	-234.500800	-234.530716	-234.627475

Figure 6. Graph showing the variation of energies at different temperatures.

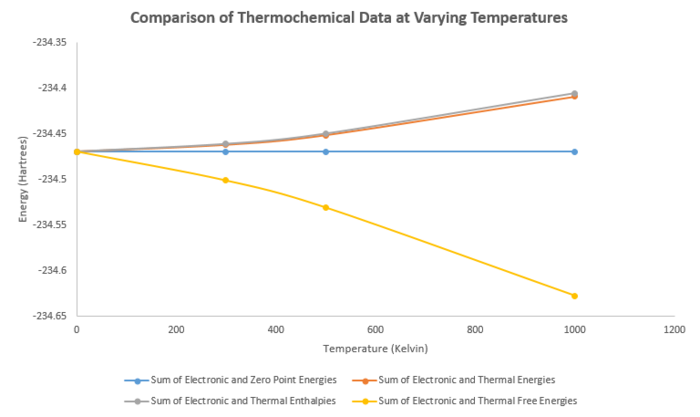
It can be seen from the data above that at 0k all 4 energies are the same, as there is no thermal energy contribution. As the temperature increases, the sum of electronic and zero point energies remains the same. The sum of electronic and thermal energies and enthalpies both increase to a higher energy as temperature increases, from the graph it can be noted that the rate of increase is almost the same for both. The sum of electronic and thermal free energies decreases to a lower energy as temperature increases. These changes in energy are as expected, as the thermal energies and entropies increase as temperature increases, while the free energies decrease.

Nf710 (talk) 14:30, 10 February 2016 (UTC) Excellent comparison at different temperatures

Optimisation of Boat and Chair Transition Structures

Next the transition structure of the Cope rearrangement was found. The boat and chair transition structures were studied to find which one gave the lowest activation energy for the reaction. This was done using the HF/3-21G level of theory with 3 different methods; finding the chair transition structure by optimising with TS(Berny), optimising with the use of frozen coordinates, and finding the boat transition structure by optimising using the QST2 method.

Optimisation of Allyl fragment

Initially an allyl fragment was drawn and optimized using the HF/3-21G level of theory. The results for this can be seen below.

Molecule	Jmol Structure	Energy (Hartrees)	Point Group	Summary of Results
Allyl Fragment		-115.82304010	C2v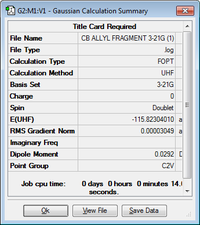

Optimisation of Chair Transition Structure

Using "Guess" Transition Structure Method

The optimised allyl fragment was duplicated and the two fragments were placed together in a staggered conformation with separation of the terminal carbons at 2.2 Å, in order to form a guess structure for the chair transition state. The guess chair structure was optimized to a transition state by optimizing using to a TS(Berny). The results are shown below.

Jmol Structure	Energy (Hartrees)	Summary of Results
	-231.61932157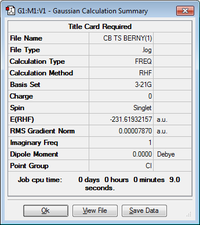

The calculation converged and formed the chair transition structure. Frequency analysis found the negative imaginary frequency that was, as discussed before, indicative of the transition structure. The value for this imaginary frequency was -817.85cm^-1.

Imaginary Frequency Vibration that leads to the Cope Rearrangement.

Optimisation using Frozen-Coordinate Method

The chair transition state can also be obtained using the frozen coordinate method. The guess structure used before with the two optimized allyl fragments was used again, the separation between terminal carbons was once again 2.2 Å but this time the separation was frozen in place. The structure was then optimized using the HF/3-21G level of theory. After this the bond breaking/forming distance were optimized, once again using the HF/3-21G level of theory. This produced the chair transition state as shown below.

Jmol Structure	Energy (Hartrees)	Summary of Results
	-231.61932233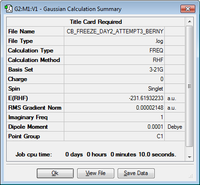

As expected, an imaginary frequency was found for the transition state at -817.88cm^-1.

Imaginary Frequency Vibration that leads to the Cope Rearrangement.

Comparing Methods

Both methods gave an imaginary frequency confirming the transition state was found. Comparing the bond breaking and forming distances for the chair structure, it can be seen that values are very similar for both methods. The bond forming lengths are very close, with the breaking length being slightly shorter for the frozen method. However the difference is not very significant and it can be concluded that both methods are good at producing the geometry of the transition state.

Method	Bond Breaking Length (Å)	Bond Forming Length (Å)
Guess Transition Structure	1.38918	2.02132
Frozen Transition Structure	1.38929	2.02073

Optimisation of Boat Transition Structure

Using the QST2 Method

The boat transition structure was optimized using the QST2 method using HF/3-21G level of theory. This is done by the calculation interpolating between the reactant and product to reach an energy maxima and hence find the transition state between them. It is necessary to label the molecules for this calculation to be done, as shown below.

Figure 7. Labeling of atoms for initial structure.

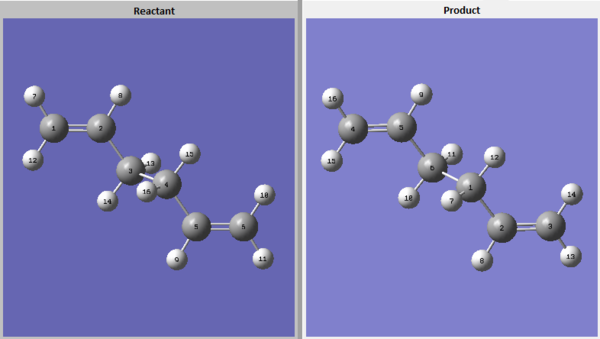
Initial attempts at optimizations resulted in failure as the initial structure was too different to the transition state, as shown below. The process is automated and the calculation only translated the allyl but did not take into account rotation about central bonds.

Figure 8. Failed Transition State from initial QST2 calculation.

In order to make sure the optimization was successful the geometries of the product and reactant were altered to better resemble the transition state by adjusting the dihedral angle. It was then optimized again with the QTS2 calculation using the HF-3-21G level of theory.

Figure 9. Atom labeling for modified structure.

This time the boat transition structure was successfully formed. This was confirmed by the imaginary frequency at value -840.23cm^-1.

Jmol Structure	Energy (Hartrees)	Summary of Results
	-231.60280222

Imaginary Frequency Vibration that leads to the Cope Rearrangement.

Intrinsic Reaction Coordinate Analysis

The optimized chair transition structure was analysed using an intrinsic reaction co-ordinate which shows the reaction pathway from the transition structure. It was found the IRC converged after 44 steps despite 50 steps being initially chosen for the calculation. It is only necessary to run the IRC in the forward direction due to the symmetry of the reaction coordinate. The total energy can be seen to start at a maximum which is the transition state and it falls off to the minimum of the reactants or products. The RMS gradient can be seen to go to 0 confirming that the local minimum had been found. The IRC was run at the HF-3-21G level theory as it must match that of the optimized structure.

Figure 10. Total energy and RMS Gradient along the IRC for the optimised Chair strucutre.

To confirm that the reaction converged and is symmetrical, the IRC was run again at 70 steps and in both directions. The results below can be seen to show that the curve is a mirror image from either side, justifying the use of only one direction. The IRC also converged at 44 steps again as shown by RMS gradient reaching 0.

Figure 10. Total energy and RMS Gradient along the IRC, run in both directions and for 70 steps for the optimized Chair structure.

After running the IRC the molecule found at the end at the minimum was taken and reoptimised to a minimum using the HF/3-21G level of theory. This was done to find which conformer was obtained. The results for this can be seen below, with the energy found corresponding to the gauche2 conformer.

Nf710 (talk) 14:32, 10 February 2016 (UTC) correct frequencies energies and conformer

Jmol Structure	Energy (Hartrees)	Summary of Results
	-231.69166702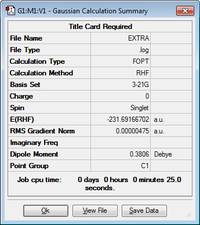

Activation Energy

In order to find the activation energies of the two transition states, the HF/3-21G optimised structures were reoptimised using the B3LYP/6-31G(d) level of theory. This was done by optimising to a TS(Berny) as before, the results for the reoptimisations can be seen below.

The results of the reoptimisation of the Boat transition structure can be seen below, an imaginary frequency of -530.36cm^-1 was found.

Jmol Structure	Energy (Hartrees)	Summary of Results
	-234.54309307

Imaginary Frequency Vibration that leads to the Cope Rearrangement.

The results of the reoptimisation of the Chair transition structure can be seen below, an imaginary frequency of 565.54cm^-1 was found.

Jmol Structure	Energy (Hartrees)	Summary of Results
	-234.55698303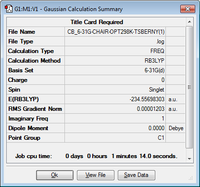

Imaginary Frequency Vibration that leads to the Cope Rearrangement.

Using the reoptimised transition structures, the activation energies for the reactant can be calculated. This is done by looking at the thermochemical properties of the optimised anti2 reactant and the reoptimised chair and boat transition states. These thermochemical properties are listed below.

	HF/3-21G			B3LYP/6-31G(d)
	Electronic energy (Hartrees)	Sum of electronic and zero-point energies at 0 K (Hartrees)	Sum of electronic and thermal energies at 298.15 K (Hartrees)	Electronic energy (Hartrees)	Sum of electronic and zero-point energies at 0 K (Hartrees)	Sum of electronic and thermal energies at 298.15 K (Hartrees)
Chair Transition State	-231.619322	-231.466705	-231.461345	-234.556983	-234.414929	-234.409009
Boat Transition State	-231.602802	-231.450930	-231.445302	-234.543093	-234.402342	-234.396008
Anti2 Reactant	-231.692535	-231.539540	-231.532567	-234.611711	-234.469214	-234.461866

The activation energies listed below are calculated by taking the difference in energies between the anti2 reactant and the boat and chair transition states.

	HF/3-21G		B3LYP/6-31G*		Expt.
	0 K	298.15 K	0 K	298.15 K	0 K
ΔE (Chair)(kcal/mol)	45.704618015	44.692445998	34.064326065	33.168243213	33.5 ± 0.5
ΔE (Boat)(kcal/mol)	55.603572490	54.759572885	41.962781848	41.326487722	44.7 ± 2.0

From the table of activation energies it can be seen that the activation energy at 0k is higher than at 298k. This is expected as at 298k the presence of thermal energy helps the reactant reach the activation barrier hence less energy is needed to be input. It can also be seen that the calculations using the 6-31G9(d) level of theory were much closer to the experimental values than for HF/3-21G. By comparing the activation energies for the chair and boat transition structures it can be found that the chair structure is consistently lower in energy thus it can be concluded that the Cope Rearrangement preferentially proceeds though the lower energy pathway of the chair transition state.

Geometry Comparison

Chair	Boat

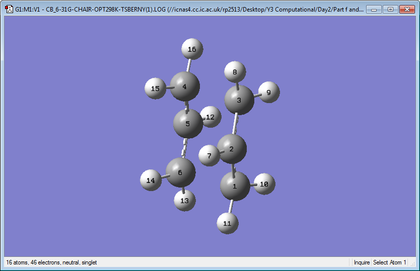
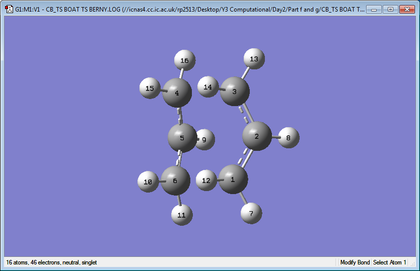
Boat	Bond Length for 3-21G (Å)	Bond Length for 6-31G(d) (Å)
C1-C2	1.38150	1.39323
C1-C6	2.13996	2.20665

Chair	Bond Length for 3-21G (Å)	Bond Length for 6-31G(d) (Å)
C1-C2	1.38930	1.40750
C1-C6	2.02072	1.96755

Comparing the geometries for the two different basis sets shows that the bond breaking lengths are very similar for both theories, while there is a slightly bigger difference in the bond forming lengths. However, the difference is not very significant thus is can be concluded that the geometry can be well approximated with lower levels of theory. Conversely, when looking at energy, the lower level of theory is much less precise than higher levels of theory.

Nf710 (talk) 14:47, 10 February 2016 (UTC) you have come to correct conclusion and have got the correct energies. in gerneal this has been a good report and you have gone beyond what you were asked. you could have gone into more depth with the quantum chemistry methods

Diels Alder Reaction

Background

In this next part of the study, two different Diels Alder cycloaddtion reactions were investigated. The Diels Alder reaction is a [4+2] cycloaddition and is a concerted pericyclic reaction. In this reaction two conjugated π systems react to form two new σ bonds and a ring. The reaction is usually between a electron rich diene and a electron poor dienophile, this is as the energy gap between the HOMO and LUMO is minimized, allowing for better orbital interaction. Applying the Woodward Hoffman rules to this reaction it can be seen from the equation (4q + 2)_s +(4r)_a an odd number is obtained. As an odd number is obtained from the equation the reaction is thermally allowed. The two Diels Alder cycloadditions being looked at are the reaction between ethene and cis-butadiene, and the reaction between maleic anhydride and cyclohexa-1,3-diene.

Figure 10. Ethene and cis-butadiene cycloaddition

Figure 11. Regioselectivity of the Diels-Alder cycloaddition.

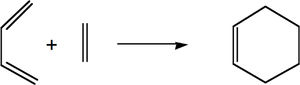
For the Diels-Alder reactions, the semi-empirical/AM1 level theory will be used for this experiement. The semi-empirical level of theory is based on the Hartree-Fock theory but is much less complex which is advantageous as using the HF method without any approximations is very expensive. AM1 calculations use the Neglect of Differential Diatomic Overlap integral approximation and uses parameters from empirical data, which makes the calculation less complex and thus favourable to use over HF.

Diels Alder Cycloaddition of Cis-Butadiene and Ethene

Optimisation of Cis-Butadiene and Ethene

To study the cycloaddition of cis-butadiene and ethene, the reactant molecules were created in GaussView and then optimised to a minimum using the Semi-Empirical/AM1 level of theory.

Cis-butadiene

The cis-butadiene was optimized as described above, with the results shown below.

Molecule	Jmol Structure	Energy (Hartrees)	Point Group	Summary of Results
Cis-butadiene		0.04879718	C2v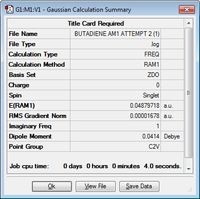

(This isn't actually the true minimum energy geometry at the AM1 level. The dihedral angle between the 4 carbon atoms shouldn't be 0. The difference in energy is negligible, but be careful that all your vibrations are positive Tam10 (talk) 16:19, 29 January 2016 (UTC))

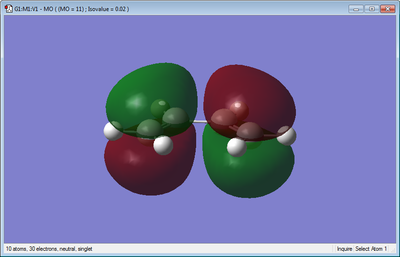
The molecular orbitals of cis-butadiene were also obtained and these can be seen visualized below.

HOMO of Cis-butadiene	LUMO of Cis-butadiene

From the visualizations above it can be seen for cis-butadiene that the HOMO is anti-symmetric and the LUMO is symmetric.

Ethene

The ethene molecule was optimised as described above, the results can be seen below.

Molecule	Jmol Structure	Energy (Hartrees)	Point Group	Summary of Results
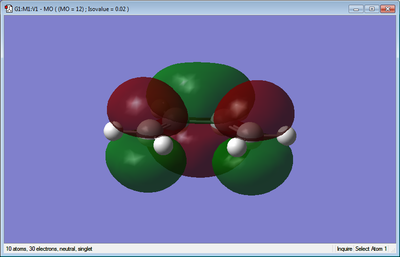
Ethene		0.02619029	D2h

The molecular orbitals of ethene were also obtained and these can be seen visualized below.

HOMO of Ethene	LUMO of Ethene

From the visualizations above it can be seen for ethene that the LUMO is anti-symmetric and the HOMO is symmetric.

Optimisation of the Transition State of the Diels-Alder Cycloaddition of Ethene and Cis-butadiene

Using the optimised structure of cis-butadiene and ethene it was then possible to determine the transition state of the Diels-Alder cycloaddition. The transition state was obtained by first creating a guess transition structure as was done earlier for the Cope rearrangement. This guess structure was formed by placing the two molecules 1.95 Å away from each other. The structure was then optimised to a TS(Berny) using the Semi-Empirical/AM1 level of theory. The results of this can be seen below.

Jmol Structure	Energy (Hartrees)	Summary of Results
	0.11165480

An imaginary vibrational frequency was found with the value of -955.76cm^-1. This confirms that the transition state has been found. The movement of the atoms towards each other represents the synchronous carbon-carbon bond formation at the ends of the molecules. The new bonds are formed at the same time in a concerted fashion.

Imaginary Frequency Vibration leading to the Diels-Alder reaction.

When examining the positive vibrational modes it can be seen that these do not contribute to the formation of the new bonds. This is exemplified by the first positive vibration at 147.15cm^-1 which shows no movement of the molecules towards or away from each other and hence no bond formation is being shown.

(Well said. It's worth looking at the vectors that correspond to each of these vibrations. The vectors of the first positive vibration are perpendicular to the reaction path Tam10 (talk) 16:19, 29 January 2016 (UTC))

First positive vibration of the transition structure.

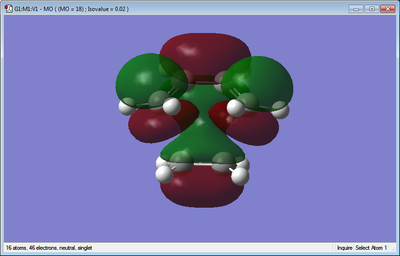
The molecular orbitals of the transition structure can also be observed, as shown below.

HOMO of Transition Structure	LUMO of Transition Structure

It can be seen that the HOMO of the transition structure is anti-symmetric and the LUMO is symmetric. For the cycloaddition of the reactants the interacting orbitals must be of the same symmetry so the overlap intergral is non-zero. By looking at the HOMO of the transition state it can be seen that it is formed by the combination of the HOMO of cis-butadiene with the LUMO of ethene, which are both anti-symmetric. The LUMO of the transition state is made up of the LUMO of cis-butadiene and the HOMO of ethene, both of these are symmetric. The combinations that make up the HOMO and LUMO of the transition state have matching symmetry and matching phases when they interact thus allowing the reaction to occur.

Geometry Analysis

Figure 12. Numbering of Atoms for Transition State Structure.

Atom Number	Bond Length (Å)
C1-C2	1.38188
C2-C3	1.39750
C3-C4	1.38176
C5-C6	1.38286
C1-C5	2.11881
C4-C6	2.11979

The Van-Der-Waals radius of a carbon atom is 1.70 Å, while the average bond lengths for a single and double carbon-carbon bonds are 1.33 Å and 1.54 Å respectively. It was seen that the distance between C1-C5 and C4-C6 are around 2.12 Å this is much less than double the Van-Der-Waal radius of a carbon atom, indicating there is some bonding interaction as a new single bond is formed. The bond lengths for C1-C2, C3-C4 and C5-C6 were seen to be around 1.38 Å, this is longer than the average double bond length suggesting they are elongating as they turn into single bonds. The C2-C3 distance is almost 1.40 Å which is much shorter than the average single bond length suggesting the formation of a double bond. The distance between carbon atoms in the transition structure displays the formation of the new bonds found in the product.

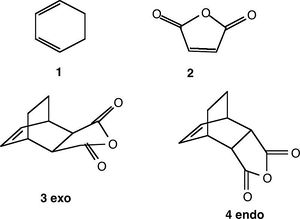
Diels-Alder Cycloaddition of Maleic Anhydride and Cyclohexa-1,3-diene

The regioselectivity of the Diels Alder reaction was explored by looking at the exo and endo transition states of the cycloaddition of maleic anhydride and cyclohexa-1,3-diene.

Optimisation of cyclohexa-1,3-diene

A molecule of cyclohexa-1,3-diene was drawn in Gaussview and optimised to a minimum using the Semi-Empirical/AM1 level of theory. The results for this can be seen below.

Molecule	Jmol Structure	Energy (Hartrees)	Point Group	Summary of Results
Cyclohexa-1,3-diene		0.02771128	C2

The molecular orbitals of cyclohexa-1,3-diene were also obtained and these can be seen visualized below.

HOMO of Cyclohexa-1,3-diene	LUMO of Cyclohexa-1,3-diene

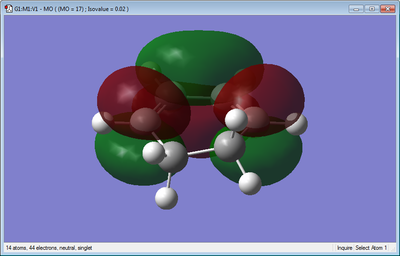
It can be seen from the visualizations above that for cyclohexa-1,3-diene the HOMO is anti-symmetric and the LUMO is symmetric.

Optimisation of Maleic Anhydride

A molecule of maleic anhydride was drawn in Gaussview and optimised to a minimum using the Semi-Empirical/AM1 level of theory. The results for this can be seen below.

Molecule	Jmol Structure	Energy (Hartrees)	Point Group	Summary of Results
Maleic Anhydride		-0.12182421	C2v

The molecular orbitals of maleic anhydride were also obtained and these can be seen visualized below.

HOMO of Maleic Anhydride	LUMO of Maleic Anhydride

It can be seen from the visualizations above that for maleic anhydride the LUMO is anti-symmetric and the HOMO is symmetric.

Exo Transition Structure

Using the optimised reactants as done earlier, a guess structure with a seperation of 1.95 Å was formed. The reactants were placed in a orientation as to ressemble the exo transition state. This guess structure was optimised to a TS(Berny) using the Semi-Empirical/AM1 level of theory. The results for this reaction can be seen below.

Jmol Structure	Energy (Hartrees)	Summary of Results
	-0.05041982

An imaginary vibrational frequency was found with the value of 812.51cm^-1. This confirms that the transition state has been found. It can be seen by the movement of the atoms towards each other, that there is synchronous carbon-carbon bond formation.

Imaginary Frequency Vibration leading to the Diels-Alder reaction.

The molecular orbitals of the transition structure can also be observed, as shown below.

HOMO of Exo Transition Structure	LUMO of Exo Transition Structure

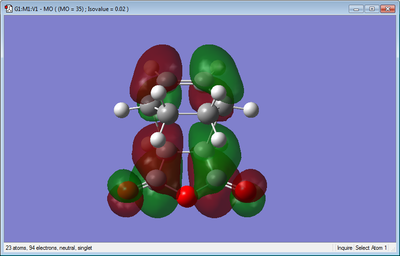
For the molecular orbitals, it can be seen that both the HOMO and LUMO are anti symmetric.

Endo Transition Structure

Once again a guess transition structure was formed, this time by placing the optimised reactants in a orientation that resembles the endo transition state. The guess structure was then optimised to a TS (Berny) using the Semi-Empirical/AM1 level of theory.

Jmol Structure	Energy (Hartrees)	Summary of Results
	-0.05150479

An imaginary vibrational frequency was found with the value of 806.33cm^-1. This confirms that the transition state has been found. It can be seen by the movement of the atoms towards each other, that there is synchronous carbon-carbon bond formation.

Imaginary Frequency Vibration leading to the Diels-Alder reaction.

The molecular orbitals of the transition structure can also be observed, as shown below.

HOMO of Endo Transition Structure	LUMO of Endo Transition Structure

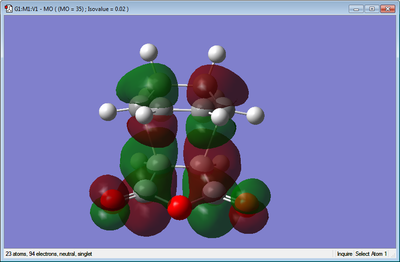
For the molecular orbitals, it can be seen that both the HOMO and LUMO are anti symmetric.

Comparing Endo and Exo Transition States

The energies and geometries of the endo and exo transition state conformers were compared and analysed.

Energy Comparison

The thermochemical data for the reactants and transition states have been extracted and are given below. Using this data, the activation energies for the endo and exo transition states have been calculated.

	AM1 Semi-Empirical
	Electronic energy (Hartrees)	Sum of electronic and zero-point energies (Hartrees)	Sum of electronic and thermal energies (Hartrees)
		0 K	298.15 K
Exo TS	-0.050420	0.134883	0.144883
Endo TS	-0.051505	0.133493	0.143682
Cyclohexa-1,3-diene	0.027711	0.152502	0.157726
Maleic anhydride	-0.121824	-0.063347	-0.058194

	AM1 Semi-Empirical
	0 K	298.15 K
ΔE Exo TS (kcal/mol)	28.69473155	28.45816066
ΔE Endo TS (kcal/mol)	27.82249404	27.70452235

From the data in the tables above it can be seen that the endo transition state has a lower activation energy that the exo. This shows that the cycloaddition between cyclohex-1,3-diene and maleic anhydride preferentially occurs through the endo transition state as it is lower in activation energy and hence is the kinetic pathway.

Comparison of Geometry

Exo Transition Structure	Endo Transition Structure

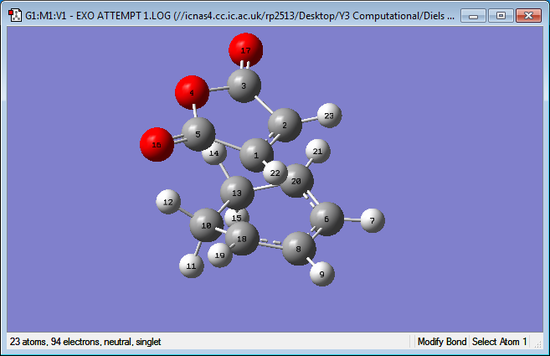
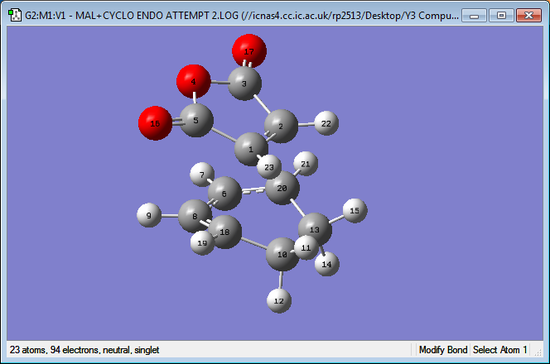
Atoms	Exo Bonds (Å)	Endo Bonds (Å)
C1-C2	1.41016	1.40852
C1-C5	1.48815	1.48925
C1-C18	2.17012	2.16234
C8-C18	1.39442	1.39308
C6-C8	1.39674	1.39727
C6-C20	1.39440	1.39302
C2-C20	2.17032	2.16254
O16-H12 (Exo) / O16-H9 (Endo)	2.69242	3.31661
O17-H14 (Exo) / O17-H7 (Endo)	2.69214	3.31706

The distances for the Gaussium bond lengths are only accurate to 2 decimal places as the level of error is fairly high. It can be seen that most of the bond lengths are equal at 2 decimal places however the biggest difference comes from the C2-C20 bond distance which is noticeably larger in the exo transition state when compared to the endo. This distance between atoms is where the formation of a new bond occurs, as shown by the distance being less than twice the Van-Der-Waals distance of carbon (1.70 Å). It can be seen that the endo bond forming distance is lower than exo, suggesting that there is a more favourable bonding interaction. One reason for this difference is because of the sterical interactions between the two molecules in the transition states. In the exo transition state it can be seen the distance O16-H12 and O17-H14 is 2.69 Å, this is less than Van-Der-Waals radius for hydrogen(1.20 Å) and oxygen (1.52 Å) showing there will be a disfavourable steric clash between these atoms. For the endo transition state the distance O16-H9 and O17-H7 is much longer at 3.32 Å and hence there is no interaction. Overall, the steric clash in exo prevents it from having as favourable overlap as the endo transition state. Secondary orbital interactions also help favour the endo transition state.

Secondary Orbital Interactions

Endo TS	Exo TS

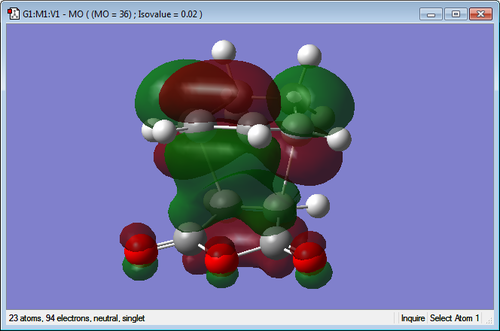
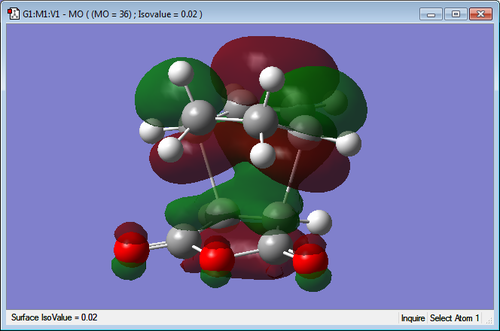
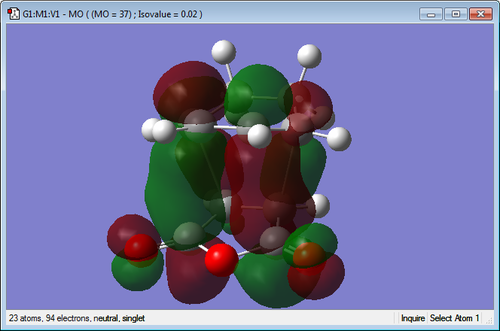
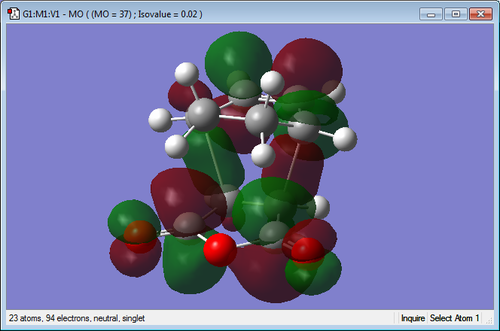
The molecular orbitals of the transition states have been visualized for the LUMO +1 and +2 of the exo and endo. It can be seen in the endo that there is a favourable interaction between the π bond system on the cyclohexa-1,3-diene and the π* orbitals of the C=O bonds on the maleic anhydride. This overlap of orbitals is good for the endo transition state as the orbitals are in close proximity. When examining the exo transition state it can be seen that this interaction is much less strong as the orbitals are positioned on the opposite end of the molecule making it much too far to interact well. This more favourable secondary orbital interaction in the endo makes the transition structure lower in energy and thus more favourable for the kinetic pathway.

(Good attempt. It's likely that there won't be a high enough population in the LUMOs to create much of an effect, however Tam10 (talk) 16:16, 29 January 2016 (UTC))

Conclusion

In conclusion, this computational experiment explored the Cope rearrangement of 1,5-hexadiene and the Diels Alder cycloaddition of butadiene and ethene and the reaction between maleic anhydride and cyclohexa-1,3-diene.

For the Cope rearrangement, the HF/3-21G and B3LYP/6-31G(d) levels of theory were used through the study. Different conformers of 1,5-hexadiene were formed and optimised. The anti2 conformer was used to compare different levels of theory. The B3LYP/6-31G(d) level of theory was found to be the most accurate, as fewer approximations are used during calculations when compared to the Hartee-Fock method. The chair and boat transition structure were constructed and optimised. The formation of these transition states was confirmed by the presence of an imaginary frequency. The activation energies were also examined and it was found that the chair transition state was of a lower energy, with the B3LYP/6-31G(d) level of theory giving the most accurate results.

The Diels alder reaction was also examined, with all the reactions being run at the Semi-empirical/AM1 level of theory. The first reaction studied was the cycloaddition of ethene and butadiene, the reactants were optimised and the transition state was found and analysed. The regioselectivity of the Diels alder cycloaddition was explored with the reaction of maleic anhydride and cylohexa-1,3-diene. The activation energies of the endo and exo transition states were found and it was seen that the endo was lower in energy and thus the preferred kinetic pathway. This was rationalised by comparing the sterics and secondary orbital interactions in the transition state, it was found that there was more steric strain in the exo and that there were more favourable orbitals interactions between the C=O π* and the π system of the diene in the endo transition state.

For further study on this experiment, the QST3 method of calculation could be used instead of QST2. This method also includes a guess transition structure in the calculation and thus gives a more accurate result. In addition, the study of inverse electron demand Diels-Alder reactions could be done to see whether this effects the transition state.