Rep:Mod:RM2DS3
Computational Module 2
Computational Analysis of BH3
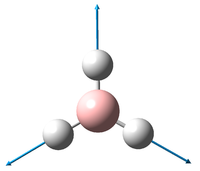
Optimising the Structure of BH3
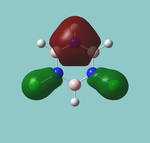
A rough trigonal planar structure of BH3 with trivial bond lengths (1.5Å) was modelled and submitted for optimisation using the B3LYP method and 3-21G basis set.
What follows is an excerpt of the output file generated by Guassian.
Item Value Threshold Converged?
Maximum Force 0.000413 0.000450 YES
RMS Force 0.000271 0.000300 YES
Maximum Displacement 0.001610 0.001800 YES
RMS Displacement 0.001054 0.001200 YES
Predicted change in Energy=-1.071764D-06
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
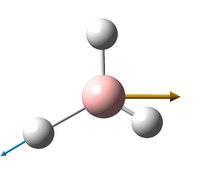
! R1 R(1,2) 1.1935 -DE/DX = 0.0004 !
! R2 R(1,3) 1.1935 -DE/DX = 0.0004 !
! R3 R(1,4) 1.1935 -DE/DX = 0.0004 !
! A1 A(2,1,3) 120.0 -DE/DX = 0.0 !
! A2 A(2,1,4) 120.0 -DE/DX = 0.0 !
! A3 A(3,1,4) 120.0 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
It can be seen that all 3 bond distances have converged to 1.19Å, while the angles have retained the ideal 120o that they started with. The bond length is in good agreement with what is observed[1]
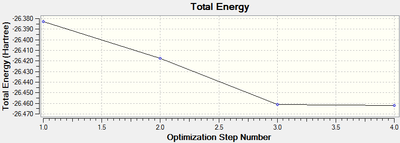
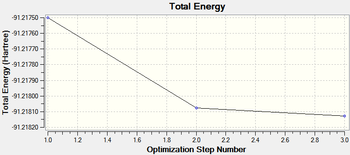
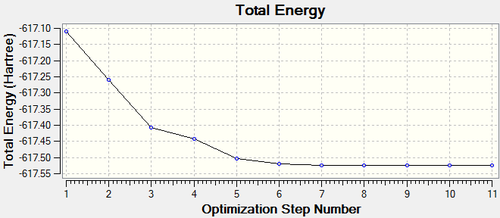
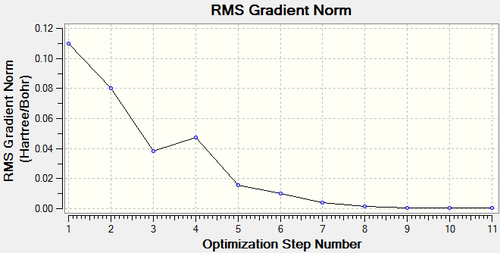
The optimisation took 4 steps, which can be seen below.
| Opimised Structure | Total energy | Animation | |||
|---|---|---|---|---|---|
|
 |
| |||
| RMS Gradient | |||||
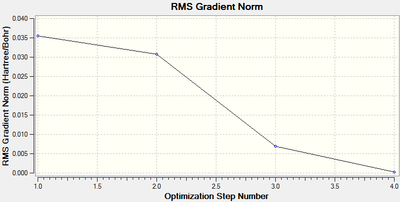
|
- ↑ Kawaguchi, K; J. Chem. Phys. 96, 3411 (1992) DOI:10.1063/1.461942
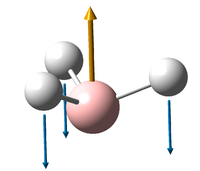
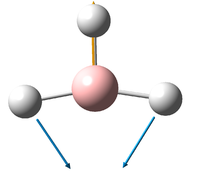
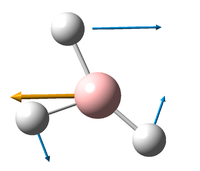
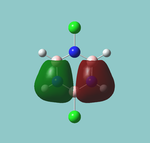
Vibrations of BH3
The following output is obtained for vibrational analysis of BH3 using B3LYP method and 3-21G basis set.
Full mass-weighted force constant matrix:
Low frequencies --- -66.7625 -66.3592 -66.3589 -0.0020 0.0031 0.2123
Low frequencies --- 1144.1483 1203.6413 1203.6424
Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman scattering
activities (A**4/AMU), depolarization ratios for plane and unpolarized
incident light, reduced masses (AMU), force constants (mDyne/A),
and normal coordinates:
1 2 3
A" E' E'
Frequencies -- 1144.1483 1203.6413 1203.6424
Red. masses -- 1.2531 1.1085 1.1085
Frc consts -- 0.9665 0.9462 0.9462
IR Inten -- 92.8665 12.3148 12.3173
Atom AN X Y Z X Y Z X Y Z
1 5 0.00 0.00 0.16 0.00 0.10 0.00 -0.10 0.00 0.00
2 1 0.00 0.00 -0.57 0.00 0.08 0.00 0.81 0.00 0.00
3 1 0.00 0.00 -0.57 -0.38 -0.59 0.00 0.14 0.38 0.00
4 1 0.00 0.00 -0.57 0.38 -0.59 0.00 0.14 -0.38 0.00
4 5 6
A' E' E'
Frequencies -- 2598.4249 2737.4364 2737.4371
Red. masses -- 1.0078 1.1260 1.1260
Frc consts -- 4.0092 4.9714 4.9714
IR Inten -- 0.0000 103.7400 103.7333
Atom AN X Y Z X Y Z X Y Z
1 5 0.00 0.00 0.00 0.11 0.00 0.00 0.00 0.11 0.00
2 1 0.00 0.58 0.00 0.02 0.00 0.00 0.00 -0.81 0.00
3 1 0.50 -0.29 0.00 -0.60 0.36 0.00 0.36 -0.19 0.00
4 1 -0.50 -0.29 0.00 -0.60 -0.36 0.00 -0.36 -0.19 0.00
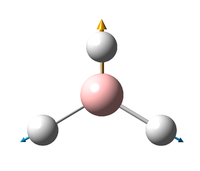
All the "low frequencies", which are just translations, are small relative to the found frequencies.
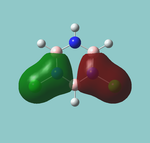
6 frequencies have been found; one of A'' and 2 degenerate pairs of E' symmetries. By finding these symmetries in the D3h character table below, it is possible to confirm which are IR active or not.
The first stretch at 1140cm-1 is allocated A''. It can more accurately be allocated as A''2 a C'2 rotation about a B-H bond will "swap" the other two hydrogen. However, they will be out of phase, and hence this is gives a result of -1 in the symmetry table, only exhibited by A''2 and not A''1.
As for A', this stretch must be A'1 as all transformations in all symmetry elements (notably C'2) give the same molecule in the correct phase.
The E' pairs are unambiguous.
According to the symmetry table, only E' and A''2 vibrations are IR active. E' has two perpendicular linear vectors in x and y, while A''2 has a single linear vector in z. This exactly what is seen in the calculations in the change in dipole caused by the vibration.
| E | 2C3 | 2C'2 | σh | 2S3 | 3σv | Linear (Rotation) | Quadratic | |
| A'1 | 1 | 1 | 1 | 1 | 1 | 1 | - | x2+y2,z2 |
| A'2 | 1 | 1 | -1 | 1 | 1 | -1 | (Rz) | - |
| E' | 2 | -1 | 0 | 2 | -1 | 0 | x,y | x2-y2,xy |
| A''1 | 1 | 1 | 1 | -1 | -1 | -1 | - | - |
| A''2 | 1 | 1 | -1 | -1 | -1 | 1 | z | - |
| E'' | 2 | -1 | 0 | -2 | 1 | 0 | (Rx,Ry) | xz,yz |
These calculations show that the E' pairs consist of two degenerate, perpendicular vibrations.
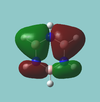
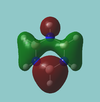
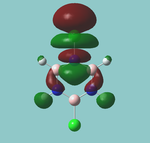
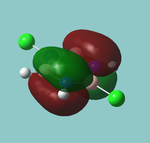
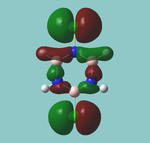
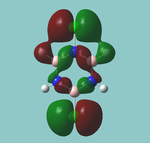
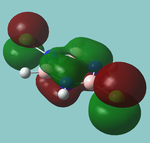
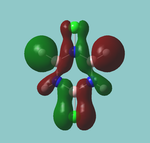
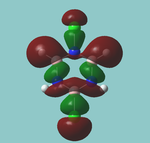
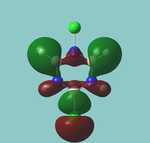
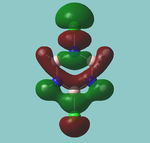
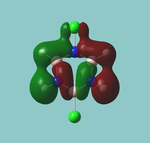
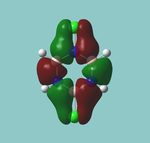
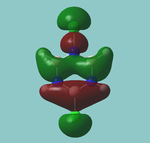
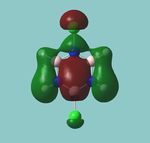
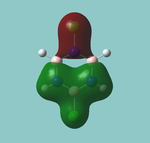
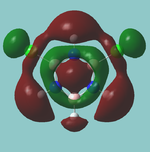
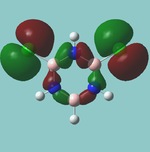
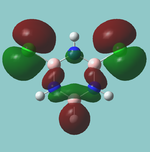
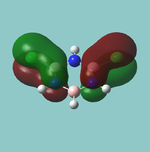
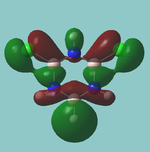
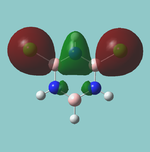
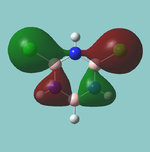
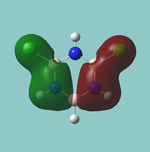
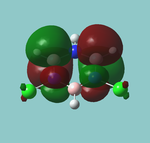
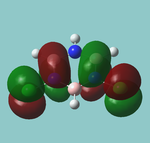
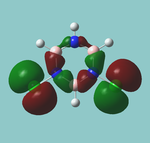
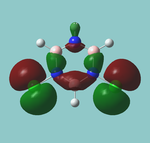
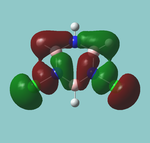
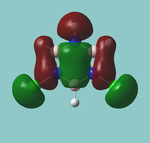
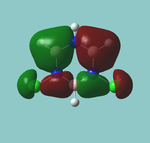
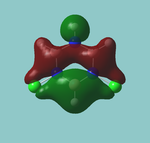
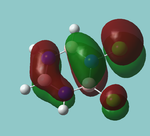
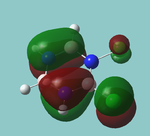
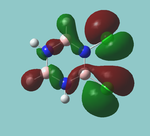
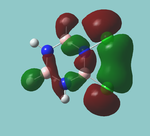
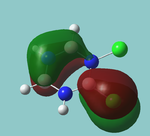
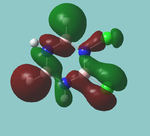
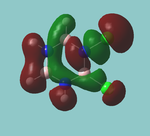
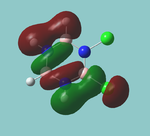
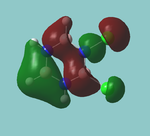
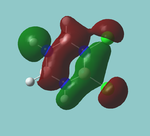
MO diagram
Calculated using B3LYP method and 6-31G basis set[1] (optimised with 6-31G).
| JMol orbitals | LCAO | |||||||
|---|---|---|---|---|---|---|---|---|
| 7 | 8 | e' | ||||||
|
|
 | ||||||
| 6 | a1' | |||||||
|
 | |||||||
| 5 | a2'' | |||||||
|
 | |||||||
| 3 | 4 | e' | ||||||
|
|
 | ||||||
| 2 | a1' | |||||||
|
 | |||||||
| 1 | a1' | |||||||
|
||||||||
Energy Levels from Gaussan:
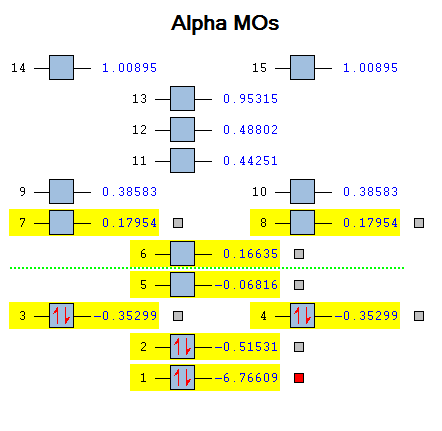
The orbitals with black filled headings are those filled with electrons (explicitly shown on Gaussian diagram)
The LCAO approach actually yields fairly accurate representations for most of the MO's shown. The least accurate are the highest degenerate pair, which with a bit of imagination can be fitted, but the exact positioning and shape of the nodes is not accurately shown. The second highest MO is also not too accurate with respect to its coefficients. Overall however, for a relatively simple method, it provides an excellent qualitative description of molecular orbitals.
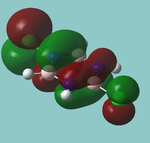
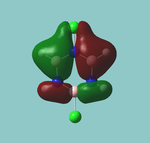
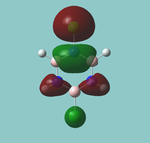
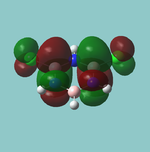
NBO analysis
| By Colour | ||
|---|---|---|
 | ||
| ||
| Values | ||
 | ||
In the .out file, it is seen a below:
Summary of Natural Population Analysis:
Natural Population
Natural -----------------------------------------------
Atom No Charge Core Valence Rydberg Total
-----------------------------------------------------------------------
B 1 0.27845 1.99954 2.72201 0.00000 4.72155
H 2 -0.09282 0.00000 1.09266 0.00015 1.09282
H 3 -0.09282 0.00000 1.09266 0.00015 1.09282
H 4 -0.09282 0.00000 1.09266 0.00015 1.09282
=======================================================================
* Total * 0.00000 1.99954 6.00000 0.00046 8.00000
Further information can be obtained from the .out file:
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
1. (1.99856) BD ( 1) B 1 - H 2
( 45.36%) 0.6735* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 0.0000 0.0000
0.8165 0.0000 0.0000 0.0000
( 54.64%) 0.7392* H 2 s(100.00%)
1.0000 0.0001
2. (1.99856) BD ( 1) B 1 - H 3
( 45.36%) 0.6735* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 0.7071 0.0000
-0.4082 0.0000 0.0000 0.0000
( 54.64%) 0.7392* H 3 s(100.00%)
1.0000 0.0001
3. (1.99856) BD ( 1) B 1 - H 4
( 45.36%) 0.6735* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 -0.7071 0.0000
-0.4082 0.0000 0.0000 0.0000
( 54.64%) 0.7392* H 4 s(100.00%)
1.0000 0.0001
4. (1.99954) CR ( 1) B 1 s(100.00%)
1.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000
5. (0.00000) LP*( 1) B 1 s(100.00%)
6. (0.00000) RY*( 1) B 1 s( 0.00%)p 1.00(100.00%)
7. (0.00000) RY*( 2) B 1 s( 0.00%)p 1.00(100.00%)
8. (0.00000) RY*( 3) B 1 s( 0.00%)p 1.00(100.00%)
9. (0.00000) RY*( 4) B 1 s( 0.00%)p 1.00(100.00%)
The first three are bonding orbitals (BD) made of approximately equal parts (though actually in a slight excess towards boron). Within this bonding orbital, the hydrogen contribution is fully (100%) s in character (of course), while the boron contribution is ⅓ s and ⅔ p in character. In other words, this contribution is formally from an sp2 hybrised orbital.
The B core (CR) is purely s, as expected, however, the B lone pair is also assigned s. Something may have gone wrong in the calculation. It may be the case that the program has allocated the LP to the 3s (Rydberg) orbital instead of the 2p (valence) which is shown at 6. In fact, this does seem to be what happend as there are 4 RY p orbitals following the "s" lone pair, which must correspond to 3px/y/z and the "missing" 2pz orbital.
The Ground State Structure of TlBr3
Optimising TlBr3 using the B3LYP method and LANL2DZ basis set yields the following output[1], which confirms its convergence.
Item Value Threshold Converged?
Maximum Force 0.000002 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000022 0.001800 YES
RMS Displacement 0.000014 0.001200 YES
Predicted change in Energy=-6.083913D-11
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 2.651 -DE/DX = 0.0 !
! R2 R(1,3) 2.651 -DE/DX = 0.0 !
! R3 R(1,4) 2.651 -DE/DX = 0.0 !
! A1 A(2,1,3) 120.0 -DE/DX = 0.0 !
! A2 A(2,1,4) 120.0 -DE/DX = 0.0 !
! A3 A(3,1,4) 120.0 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
For reference, the final energy is -91.21812851 a.u.
Bond angle is found to be 120o, and considering that D3h was forced, no other value is expected. The bond length is 2.65 Å. This is reasonable compared to the real bond length in the dihydrated complex of 2.51 Å [2]
| Final Optimised Structure of TlBr3 | Optimisation Profiles | |||
|---|---|---|---|---|
|
| |||

|
- ↑ .log output file for optimisation of TlBr3
- ↑ Glasser, J; Johansson, G Acta Chemica Scandinavica A 36 125-135 (1982) DOI:10.3891/acta.chem.scand.36a-0125
Frequency Anaylsis
The obtained modes are identical as for BH3 as it is the same point group.
The following output[1] is obtained:
Low frequencies --- -3.4213 -0.0026 -0.0004 0.0015 3.9367 3.9367
Low frequencies --- 46.4289 46.4292 52.1449
Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman scattering
activities (A**4/AMU), depolarization ratios for plane and unpolarized
incident light, reduced masses (AMU), force constants (mDyne/A),
and normal coordinates:
1 2 3
E' E' A2"
Frequencies -- 46.4289 46.4292 52.1449
Red. masses -- 88.4613 88.4613 117.7209
Frc consts -- 0.1124 0.1124 0.1886
IR Inten -- 3.6867 3.6867 5.8466
Atom AN X Y Z X Y Z X Y Z
1 81 0.00 0.28 0.00 -0.28 0.00 0.00 0.00 0.00 0.55
2 35 0.00 0.26 0.00 0.74 0.00 0.00 0.00 0.00 -0.48
3 35 0.43 -0.49 0.00 -0.01 -0.43 0.00 0.00 0.00 -0.48
4 35 -0.43 -0.49 0.00 -0.01 0.43 0.00 0.00 0.00 -0.48
4 5 6
A1' E' E'
Frequencies -- 165.2685 210.6948 210.6948
Red. masses -- 78.9183 101.4032 101.4032
Frc consts -- 1.2700 2.6522 2.6522
IR Inten -- 0.0000 25.4830 25.4797
Atom AN X Y Z X Y Z X Y Z
1 81 0.00 0.00 0.00 0.42 0.00 0.00 0.00 0.42 0.00
2 35 0.00 -0.58 0.00 0.01 0.00 0.00 0.00 -0.74 0.00
3 35 0.50 0.29 0.00 -0.55 -0.32 0.00 -0.32 -0.18 0.00
4 35 -0.50 0.29 0.00 -0.55 0.32 0.00 0.32 -0.18 0.00
The low frequencies are all approxiatly zero.
| E' | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
| ||||||||||
| A''2 | ||||||||||||
|
| |||||||||||
| A'1 | ||||||||||||
|
| |||||||||||
| E' | ||||||||||||
|
|
| ||||||||||
Frequency analysis is important because it allows us to determine whether the structure we have obtained is actually a minimum. If the atoms lie on a potential gradient and not on a minimum, the structure cannot, in the strict definition, oscillate. The structure must be perturbed from a minimum where it is motionless. From its new position it experiences a restoring force with an associated force constant. If the system is on a potential gradient and the system is perturbed down this gradient, it will have a negative force constant as the "restoring" force is away from the center i.e. down the potential gradient. This results in erroneous vibrational calculations that give negative values, which are clearly impossible; a vibration cannot take less than 0 seconds, or have a negative energy.
For this reason, it is important to use exactly the same method and basis set for the optimisation and the vibrational analysis. Different methods will yield different minima, and optimising with one method, then applying another will mean that the atoms are not in the minima a determined by the new method. In other word, the minima determined by different methods will be different themselves.
The 6 "Low Frequencies" are due to movements in the center of mass; 3 translations and 3 rotations. Ideally, these degrees of freedom do not invoke any movement of atoms relative to each other. However, if the real center of mass is not perfectly positioned in the moelcule's potential field, and in this case it is not due to some inadequacies in the calculation, these degrees of freedom will result in some movement of atoms relative to each other, resulting in an oscillation about the center of mass hence give a "frequency". The smaller the frequency, the smaller the "oscillation" about the center of mass and the closer the calculation was to reality.
In these calculations, some bonds were not defined. This is because GaussView defines bonds as specific distances between atoms and are not related to any bonding interactions in the molecular orbitals.
"Bonds" do not exist as such; they are just a construct to help explain molecular interactions. However, "bond distances" do. As in, they are the distances between two minima in energy wells created by the interactions of atomic nuclei and electrons.
By placing multiple atoms close enough to each other in a region of space, all the electrons interact with all the nuclei, and each with themselves, to form a potential energy surface, much like the potential surfaces around a single nuclei (atomic orbitals). On this potential energy surface, there are minima for both the nuclei (the equilibrium positions) and the electrons (molecular orbitals). The case is much more complex for electrons, with quantised energy levels being formed (so not technically "minima") and them being filled in accordance with Pauli's exclusion principle etc.. More to the point, these minima can result in a stable configuration for the atoms, and so exists as a molecule. Hence, a molecule is not a collection of atoms held together by a series of bonds, but rather particularly favourable electrostatic interactions and quantum effects between specific atoms.
Cis and Trans Isomers of Mo(CO)4(Cl)2
Loose optimisation of cis-Mo(CO)4(Cl)2
 |
|
|
It is clear that an initial "loose" optimisation is required for these molecules; a more rigorous method would have taken far longer.
In the animation, it is seen that the bonds "disappear" but the reason for this is trivial. Gaussview defines and alloactes bonds following the criterion of length. In inorganic complexs, the interatomic distances may exceed these conventional lengths and are not definied. However, the "bonds" as such, are still present.
The LANL2MB loose optimisations for cis[1] and for the trans[2] isomers
- ↑ LANL2MN for cis DOI:10042/to-12946
- ↑ LANL2MN for transDOI:10042/to-12947
LANL2DZ
Optimisation of Cis
The following output[1] was obtained:
Item Value Threshold Converged?
Maximum Force 0.000022 0.000450 YES
RMS Force 0.000006 0.000300 YES
Maximum Displacement 0.001502 0.001800 YES
RMS Displacement 0.000386 0.001200 YES
Predicted change in Energy=-1.141032D-08
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 2.0117 -DE/DX = 0.0 !
! R2 R(1,3) 2.0578 -DE/DX = 0.0 !
! R3 R(1,4) 2.0116 -DE/DX = 0.0 !
! R4 R(1,5) 2.0577 -DE/DX = 0.0 ..........
All derivatives were zero. This shows how much more rigorous this method is compared those used for BH3
Mo(cis) |
Final energy: -623.57707194 a.u.
The Mo-P distance is found to be 2.5 A which is in good agreement with literature[2] which gives it as 2.3-2.4A
- ↑ LANL2DZ of cis DOI:10042/to-13182
- ↑ Alyea, E. C.; Song, S; Inorg. Chem., 1995, 34 (15), pp 3864–3873DOI:10.1021/ic00119a006
Optimisation of Trans
Similarly[1]:
Item Value Threshold Converged?
Maximum Force 0.000087 0.000450 YES
RMS Force 0.000020 0.000300 YES
Maximum Displacement 0.001711 0.001800 YES
RMS Displacement 0.000250 0.001200 YES
Predicted change in Energy=-9.692971D-08
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 2.0604 -DE/DX = 0.0 !
! R2 R(1,3) 2.0599 -DE/DX = 0.0 !
! R3 R(1,4) 2.0604 -DE/DX = 0.0 !
! R4 R(1,5) 2.0599 -DE/DX = 0.0 !
! R5 R(1,10) 2.4449 -DE/DX = 0.0 !
! R6 R(1,11) 2.4449 -DE/DX = 0.0 !
! R7 R(2,9) 1.1726 -DE/DX = 0.0001 ..........
For trans however, a few derivatves vary from 0.0001 to -0.0001. Still, this is a much greater degree of accuracy than before.
Mo(cis) |
Final energy: -623.57603101
- ↑ LANL2DZ of trans DOI:10042/to-13183
Comparison of Energies
The Trans isomer is lower in energy by 1x10-3 Hartrees, which is 2.6 kJmol-1. This means at room temperature the interconversion is slightly too high in energy to be feasible. However, they could interconvert with slight heating above approximately 41oC, though this would depend on kinetic factors too.
This agrees with literature which states that the cis isomers of the form Mo(CO)4L2 will thermally isomerise to the trans [1]
- ↑ Darensbourg, D. J.; Kump, R. L.; Inorg. Chem., 1978, 17 (9), pp 2680–2682 DOI:10.1021/ic50187a062
Frequency analysis of cis isomer
From the output file[1]:
Low frequencies --- -1.8030 -0.0006 0.0002 0.0004 0.9927 1.4787
Low frequencies --- 10.7600 17.5994 42.0357
Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman scattering
activities (A**4/AMU), depolarization ratios for plane and unpolarized
incident light, reduced masses (AMU), force constants (mDyne/A),
and normal coordinates:
1 2 3
A A A
Frequencies -- 10.7436 17.5994 42.0357
Red. masses -- 29.7744 32.3014 19.3486
Frc consts -- 0.0020 0.0059 0.0201
IR Inten -- 0.0264 0.0073 0.0048
Atom AN X Y Z X Y Z X Y Z
1 42 0.00 0.00 -0.06 0.00 0.02 0.00 0.00 -0.03 0.00
2 6 -0.02 0.03 -0.15 0.00 0.02 -0.08 -0.02 -0.02 0.22.....
The "low frequencies" are all approximately zero, as required
- ↑ Cis isomer frequency analysis DOI:10042/to-12954
Frequency Analysis of trans Isomer
From the output file[1]:
Low frequencies --- -2.2287 -1.6296 0.0005 0.0005 0.0006 3.0289
Low frequencies --- 5.1336 6.2031 37.2052
Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman scattering
activities (A**4/AMU), depolarization ratios for plane and unpolarized
incident light, reduced masses (AMU), force constants (mDyne/A),
and normal coordinates:
1 2 3
A A A
Frequencies -- 4.9159 6.1123 37.2052
Red. masses -- 21.7853 34.6920 27.0447
Frc consts -- 0.0003 0.0008 0.0221
IR Inten -- 0.0941 0.0000 0.4187
Atom AN X Y Z X Y Z X Y Z
1 42 0.00 0.00 0.04 0.00 0.00 0.00 0.00 -0.17 0.00
2 6 0.00 0.21 0.04 0.04 0.00 0.00 0.00 -0.25 0.00....
The same is true for the trans isomer, however, the actual lowest actual frequency (5cm-1) is less than double the highest non-frequency (3cm-1) which may mean there is significant error in the lower vibrational frequencies. However, as we are discussing stretches which appear in the 1000cm-1 range, we can assume some degree of accuracy for our purposes.
- ↑ Trans isomer frequency analysis DOI:10042/to-12955
Comparison of Frequency Analyses
Both cis and trans isomer have 4 CO stretching modes. In the cis isomer, they are all active, while in the trans, 2 are essentially IR inactive, as expected based on symmetry.
| cis | trans | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| One pair of either cis or trans CO out of phase | |||||||||||||||
|
|
|
| ||||||||||||
| One pair of trans CO out of phase | |||||||||||||||
|
|
|
| ||||||||||||
| Pairs above in phase, but out of phase with each other | |||||||||||||||
|
|
|
| ||||||||||||
| All in phase | |||||||||||||||
|
|
|
| ||||||||||||
|
|
As expected, there are fewer peaks in the trans spectrum due to some of the CO vibrational (and some lower modes) being rendered IR inactive by the higher level of symmetry (the trans isomer approaches C2v).
The cis compound has the following carbonyl frequencies[1]: 2072cm-1 2004cm-1 1994cm-1 and 1986cm-1. The computed values seem reasonable, though they are all slightly lower than they should be.
- ↑ Alyea, E. C.; Song, S; Inorg. Chem., 1995, 34 (15), pp 3864–3873 DOI:10.1021/ic00119a006
LANL2DZ Extra Basis: Incorporating d Orbitals
Optimisation of Cis
The following output was obtained using the extrabasis function, and assigning the phorporous d orbitals[1]:
Item Value Threshold Converged?
Maximum Force 0.000138 0.000450 YES
RMS Force 0.000044 0.000300 YES
Maximum Displacement 0.001119 0.001800 YES
RMS Displacement 0.000403 0.001200 YES
Predicted change in Energy=-2.355661D-07
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 2.0207 -DE/DX = 0.0 !
! R2 R(1,3) 2.0547 -DE/DX = 0.0 !
! R3 R(1,4) 2.0207 -DE/DX = 0.0 !
! R4 R(1,5) 2.0547 -DE/DX = 0.0 !
! R5 R(1,10) 2.4761 -DE/DX = 0.0 !
! R6 R(1,11) 2.4761 -DE/DX = 0.0 !
! R7 R(2,6) 1.1764 -DE/DX = 0.0 !
! R8 R(3,8) 1.1748 -DE/DX = -0.0001 ........
Mo(cis) |
Total energy: -623.69291205 a.u.
Optimisation of Trans
Similarly[2]:
Item Value Threshold Converged?
Maximum Force 0.000026 0.000450 YES
RMS Force 0.000009 0.000300 YES
Maximum Displacement 0.001629 0.001800 YES
RMS Displacement 0.000366 0.001200 YES
Predicted change in Energy=-3.043310D-08
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 2.057 -DE/DX = 0.0 !
! R2 R(1,3) 2.0574 -DE/DX = 0.0 !
! R3 R(1,4) 2.057 -DE/DX = 0.0 !
! R4 R(1,5) 2.0559 -DE/DX = 0.0 ..........
All derivatives found to be zero.
Mo(trans) |
Final Energy: -623.69415608 a.u.
Comparison of Energies
The extrabasis seems to give the opposite result, with the cis being more stable by 1.2x10-3 or 3.1 kJmol-1, which is an even bigger difference than obtained with the previous method.
This is probably due to some error in calculation (I do not have time to run it again), but it may also be that the method predicts a trans effect from the newly introduced d orbitals from phorphorous. In reality PCl3 is only a weak π acceptor[3], so sudden preference for cis on the introduction of d orbitals seems unlikely.
- ↑ LANL2DZ (extrabasis) for cis DOI:10042/to-13184
- ↑ LANL2DZ (extrabasis) trans DOI:10042/to-13187
- ↑ Alyea, E. C.; Song, S.; Inorg. Chem., 1995, 34 (15), pp 3864–3873 DOI:10.1021/ic00119a006
Frequency Analysis of cis
From the output file[1]:
Low frequencies --- -1.3136 0.0001 0.0003 0.0006 0.7651 1.9300
Low frequencies --- 11.7493 20.2787 45.8812
Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman scattering
activities (A**4/AMU), depolarization ratios for plane and unpolarized
incident light, reduced masses (AMU), force constants (mDyne/A),
and normal coordinates:
1 2 3
A A A
Frequencies -- 11.7307 20.2787 45.8811
Red. masses -- 29.9797 31.8716 18.5790
Frc consts -- 0.0024 0.0077 0.0230
IR Inten -- 0.0163 0.0042 0.0008
- ↑ LAN2DZ, extrabasis frequencey analysis of cis isomer DOI:10042/to-12962
Frequency Analysis of trans
From the output file[1]:
Low frequencies --- -2.2968 -1.9640 -0.0005 -0.0005 -0.0001 2.8560
Low frequencies --- 4.5717 7.0028 40.4800
Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman scattering
activities (A**4/AMU), depolarization ratios for plane and unpolarized
incident light, reduced masses (AMU), force constants (mDyne/A),
and normal coordinates:
1 2 3
A A A
Frequencies -- 4.4439 6.9679 40.4800
Red. masses -- 22.2701 34.5979 25.8816
Frc consts -- 0.0003 0.0010 0.0250
IR Inten -- 0.0547 0.0000 0.1130
- ↑ LAN2DZ, extrabasis frequencey analysis of trans isomer DOI:10042/to-12963
LANL2DZ vs LANL2DZ with extrabasis
| CO Mode | 1 | 2 | 3 | 4 | ||
|---|---|---|---|---|---|---|
| cis | LANL2DZ | Frequency cm-1: | 1945 | 1949 | 1958 | 2023 |
| Intensity: | 763 | 1499 | 933 | 598 | ||
| LANL2DZ (extrabasis) | Frequency cm-1: | 1938 | 1942 | 1952 | 2019 | |
| Intensity: | 1605 | 813 | 588 | 545 | ||
| trans | LANL2DZ | Frequency cm-1: | 1950 | 1951 | 1977 | 2031 |
| Intensity: | 1475 | 1467 | 0 | 4 | ||
| LANL2DZ (extrabasis) | Frequency cm-1: | 1939 | 1940 | 1967 | 2026 | |
| Intensity: | 1606 | 1606 | 6 | 5 |
The extrabasis method demonstrates the degeneracy of the two asymmetric trans stretches (especially with regards to intensity) in the trans complex much more strongly than the previous method.
It is also noted that the extrabasis method predicts slightly lower frequencies for most modes. The fact that the IR inactive modes become more "IR active" (intensity increases) on the extrabasis calculation supports (but does not prove) the fact that something may have gone wrong.
| LANL2DZ | LANL2DZ Extrabasis | |
|---|---|---|
| Cis |  |
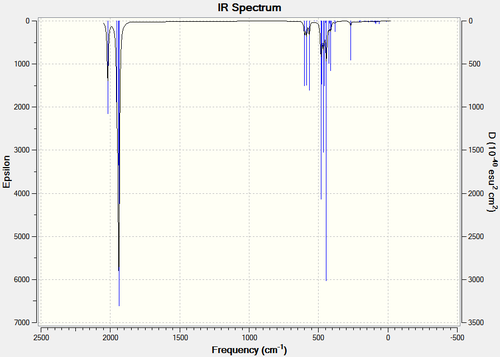
|
| Trans | 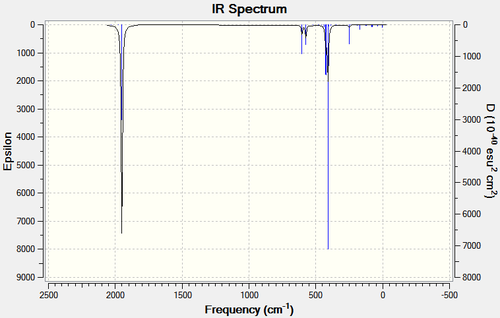 |
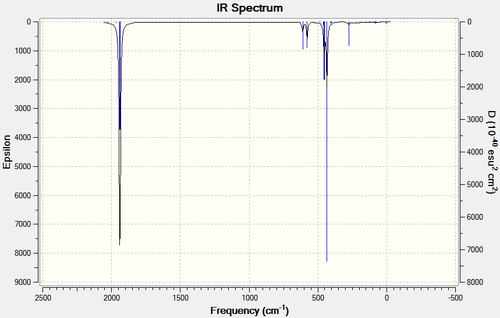
|
Both methods predict fairly similar spectra. The only noticable difference is a slight variance in the intensities.
Borazine
A theoretical study into unsymmetrically substituted chloroborazines, and an investigation as to why N-substitued borazines are rare, if even existent.
2,4,6-trichloroborazines (B substututed) are relatively common[1]. Di substituted borazines seem fairly uncommon, and N substituted even less so.
Metal borazine complexes have also been synsthesised [2], and these will be looked at very briefly.
- ↑ Beachley Jr, O. T; Inorg. Chem., 1969, 8 (12), pp 2665–2667 DOI:10.1021/ic50082a025
- ↑ Adcock, J, L; Lagowski, J. J. Inorg. Chem., 1973, 12 (11), pp 2533–2540DOI:10.1021/ic50129a009
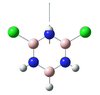
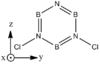
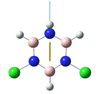
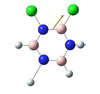
Structures
| |||
| |||
| BH bonds (1.2 A) are significantly longer than N-H bonds (1.0 A). All B-N distances are 1.43 A confirming aromaticity. B-N-B angles (123o) are slighty wider than N-B-N (117o). |
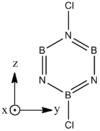 |
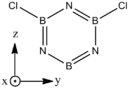 |
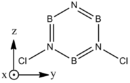 |
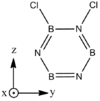
| ||||||||||||
|
|
|
| ||||||||||||
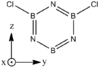
| B-Cl (1.8 A) are slightly longer than N-Cl (1.7 A). There is not much deviation from the other bond distances in borazine. The ring tends to distort so that it is "pinched in" slightly at N vertices so that B-N-B angles are wider than N-B-N angles. | |||||||||||||||
| |||
| Classic three-legged piano stool. Ring is significantly "pinched" with B-N-B angles of 126o and N-B-N angles of 114o. B-N distances (1.5 A) are now longer indicating reduction in bonding order. Boron are eclipsed with carbonyl. |
| Compound | ΔE relative to lowest energy (kJmol-1) |
|---|---|
| Para | +270 |
| B,B'- | 000 |
| N,N'- | +550 |
| Ortho | +280 |
Clearly the Boron substituted compound is significantly more stable than the others, with the Nitrogen substituted compound being very unstable relative.
All of these were carried out after an initial optimisation with B3LYP, 3-21G:
6-31G(d,p) optimisation of borazine DOI:10042/to-13200
6-31G(d,p) optimisation of borazine (D3h) DOI:10042/to-13204 used for MO, did not have time to rerun frequency analysis.
6-31G(d,p) optimisation of Ortho DOI:10042/to-13201
6-31G(d,p) optimisation of B,B'- DOI:10042/to-13203
6-31G(d,p) optimisation of N,N''- DOI:10042/to-13205
6-31G(d,p) optimisation of Para DOI:10042/to-13202
6-31G(d,p) optimisation of Cr complex (C3v) DOI:10042/to-13206
IR spectra
The following IR spectra were obtained using the B3LYP method with a 6-31G (d,p) basis set. A fairly rigourous basis set could be used as these are all early elements.
For the Chromium complex, the same method and basis set were used, as Chromium is still an early transition metal. This complex was found to optimise to a C3v and was hence optimised again with the point group constraint.
Frequency analysis of Borazine DOI:10042/to-13207
Frequency analysis of Para DOI:10042/to-13209
Frequency analysis of B,B''- DOI:10042/to-13210
Frequency analysis of N,N'' DOI:10042/to-13211
Frequency analysis of ortho DOI:10042/to-13208
Frequency analysis of Cr complexDOI:10042/to-13212
NH Modes
| Point Group | Compound | N-H Stretch | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D3h |  |
e' | a'1 | ||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||
| C2v |  |
b2 | a1 | ||||||||||||||||||||
|
|
|
| ||||||||||||||||||||
 |
b2 | a1 | a1 | ||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||
 |
a1 | ||||||||||||||||||||||
|
| ||||||||||||||||||||||
| Cs |  |
a' | |||||||||||||||||||||
|
|
 |
| ||||||||||||||||||||
The splitting of the N-H modes is almost negligible. As expected, the borazine IR inactive mode becomes active due to the reduction of symmetry.
BH Modes
| Point Group | Compound | B-H Stretch | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D3h |  |
a'1 | e' | ||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||
| C2v |  |
a1 | b2 | ||||||||||||||||||||
|
|
|
| ||||||||||||||||||||
 |
a1 | ||||||||||||||||||||||
|
| ||||||||||||||||||||||
 |
a1 | a1 | b2 | ||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||
| Cs |  |
a' | |||||||||||||||||||||
|
|
 |
| ||||||||||||||||||||
The BH modes show much larger differences and separations in wavenumber. This may be due to the chlorine substituents affecting the boron atoms and their bonds more they it do the nitrogen. This is further supported by the fact that all the B-H bonds are higher in wavenumber than in the parent compound. The N-H modes could shift either side.
It may also be worth noting that in the ortho compound, the BH stretch para to the BCl bond is weaker than that ortho, while for NH, the opposite is true. This might impliy that the chlorine can stabilise bond B-H para to it, while the N-H is destablised.
A final thing to note: The N-H modes are only affected in compounds with N-Cl bonds (i.e. the B,B'-disubstitued compound, the N-H compound are similar to borazine). However, all B-H are strengthened in every compound. In fact, the B-H bonds are most strengthened in the N,N'-disubstituted compound and the smallest change in the B,B'-disubstitued compound.
These observations seem to show that all B-H are strengthened by the presence of chlorine anywhere in the molecule, particularly on nitrogen, but with little effect on the N-H modes in any position.
BN Modes
| Point Group | Compound | B N Stretch 1 | B N Stretch 2 | B N Stretch 3 | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D3h | 
|
|
|
| ||||||||||||||||||
| C2v | 
|
|
|
| ||||||||||||||||||
| C2v | 
|
|
|
| ||||||||||||||||||
| C2v | 
|
|
|
| ||||||||||||||||||
| Cs | 
|
|
|
| ||||||||||||||||||
Differences in modes 1 and 2 (cm-1): para (13)= 1,3-B (13) < 1,3-N (30) <ortho (35).
The splitting of the degenerate levels increases as substituents approach each other. But because of the marked differences between the B,B'- and the N,N'-disubstituted compounds, absolute positioning cannot be the dominant factor.
"Ring Breathing" Modes (or their analogues)
Benzene has a well known breathing mode in which the ring expands and contracts. However, this cannot occur in borazine. Imagine compressing the borazine ring in the same way benzene is during ring breathing. The nitrogen atoms will experiences different forces than the boron and one would "push" in first while the other is pushed out. Instead, what seems to be observered here is that the ring breathing mode splits into two, where the breathing only involves either the boron atoms or the nitrogen atoms, which are clearly not degenerate.
A brief descriptions of the "modes" studied here:
The B and N breathing modes involve most of the movement arising from the stated atom only; the other is mostly stationary. There is usually little H wagging, and there is always two opposing hydrogen that strictly do not wag and remain straight along the resultant vector.
The "Squash" modes involve two opposing bonds being brought together. For borohydrazine, there are two perpenduclar modes that are degenerate (look for the two bonds that are brought together; for the first, it is the top and bottom, for the second, the top-left and bottom-right). As substituents are added, these quickly become distinict.
| Point Group | Compound | B breathing | N breathing | "Squash" | "Squash" | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D3h | 
|
|
|
|
| ||||||||||||||||||||||||
| C2v | 
|
|
|
|
| ||||||||||||||||||||||||
| C2v | 
|
|
|
|
| ||||||||||||||||||||||||
| C2v | 
|
|
|
|
| ||||||||||||||||||||||||
| Cs | 
|
|
|
|
| ||||||||||||||||||||||||
The strength of the B and N breathing mode increases as the number of B- and N-substituents increases respectively which is indicative of the relative stablising effects of the chlorine by conjugation, increasing the strength (force constant, k) of the bonds.
These modes are particularly important because for the C2v compounds as these become the B-Cl and N-Cl stretches.
All modes are higher in energy than their borazine counterpart expect the B breathing mode in the N,N'- compound where it actually decreases. This indicates the N-Cl linkage may actually destablise the ring.
The "squash" modes are initially degenerate in borazine. On the addition of substituents one increases in energy, while the other decreases (so to speak. Realistically, there are two resultant modes that resemble the degenerate "squashes", one of which is higher and one of which is lower). The most striking change is on the addition of ortho substituents. This may indicate this mode is most affected by the actual positioning rather than electronic effects. This also agrees with the fact the vibration decreases in energy; the "mass" of the components of the vibration has increased without any electronic stablisation (no increasing of k).
Chromium complex
On complexation to metal, the N-breathing mode does not change much, and drops slightly in energy:
| Frequency: | 859cm-1 |
| Intensity: | 25 |
|
| |
However, the B-breathing mode seems to split into two antiparallel modes with relatively large intensities, and both decreased in energy.
| (+) B Breathing | (-)B Breathing | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
 |
| ||||||||||||
|
| ||||||||||||
The diagrams show the displacement at "t=0". The N-H "wag" vectors are parallel and out of phase meaning in the sum of these vibrations, the nitrogen would not move. The B-H "wag" vectors are also out of phase with two vertical components that would cancel, but they both have in phase "outward" components, that would give rise to boron breathing in the correct manner.
This splitting indicates much more activity between the complex and the boron than with the nitrogen.
Interestingly, of the BN stretches, the lower frequency mode is relatively unaffected, only dropping by 10cm-1. However, the degenerate pair (possibly) splits as above, an one drops drops significantly by approximately 150cm-1.
| BN(1) | BN(1') | BN(2) | BN(2') | BN(3) | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
| ||||||||||||||||||||
Literature[1] stretches for hexametylated compound: 1415cm-1 1374cm-1, which are in ok agreement. One reason for better agreement with one than the other is the substituents are expected to affect the 1331cm-1 vibration more than the higher as, one could argue, this is affected more from moving to free borazine to the complex as seen above.
The BN1 stretch involves mainly N moving, which (see below) are not stronly interacting with the carbonyl groups. Hence, they do not shift much. However, in the BN2 stretchs, the B interact much more strongly and only this component of the original BN vibration is brought down in energy. This is what splits the BN degernerate set into two pairs.
The modelled carbonyl stretches are 2007 cm-1 and 2073 cm-1, slightly higher than the hexamethylated compound: 1963cm-1 and 1867cm-1. However, this may note indicate poor theory; methyl groups are electron releasing, which would increase electron density on the metal, and hence weaken the carbonyl stretch via back bonding.
A possible reason for the above effects is a strong boron interaction with the complex, as supported by the previous argument. The lowest energy stretch is a2, and inherently more symmetric than the degenerate e stretches (if viewed separately). If there is a lower potential well around B than N (because of this stronger interaction) a symmetric vibration (in particular with C3=1) will have this effect cancelled out to some extent as all the boron momenta are correlated i.e. all boron move down the potential well at the same time. If this is not the case, as in the e pair, some vectors will not cancel and the depth of the well will begin to take effect.
- ↑ Adcock, J, L; Lagowski, J. J. Inorg. Chem., 1973, 12 (11), pp 2533–2540DOI:10.1021/ic50129a009
MO and NBO anaylsis
MO analysis of borazine DOI:10042/to-13204
MO analysis of Ortho DOI:10042/to-13213
MO analysis of B,B''-DOI:10042/to-13215
MO analysis of N,N'' DOI:10042/to-13217
MO analysis of paraDOI:10042/to-13214
MO analysis of borazine DOI:10042/to-13219
For reference, Borazine
|
|
| ||||||||||||||||||||||||||
Dichloroborazines
| MO | Observation |  |
 |
 |

| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
|
|
LUMO analysis
The key observation about the LUMO and higher orbitals is that within these three, ther are no B-Cl* orbitals. There are only N-Cl* orbitals, are there as many of these are there are N-Cl bonds. It would be assumed that the N,N',N''-substituted compound would have N-Cl* orbitals as all the shown unoccupied orbitals. The B-Cl* orbitals however lie beyond the LUMO+2, meaning these bonds are kinetically more stable. It may be predicted that the B,B',B''-substituted compound maybe be exceptionally stable to substitution.
In the B,B'-compound, the LUMO actually lies on the borons themselves, meaning they may be more susceptable to attack. This begs the question if the chlorine were replaced with, say divalent oxygen, would it be possible to add further functionality to protect the LUMO orbitals. Alternatively, it may be possible to add substituents (though different to Chlorine, maybe carbon) to the N atoms, and form protective alkyl cages. By protecting one face only, it may be possible to form more stable metal complexes (as shown below, the bonding interaction in metal complexs is not that strong).
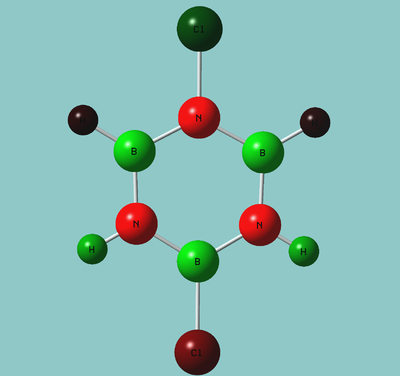
NBO Analysis of para compound
| By Colour | ||
|---|---|---|
 | ||
| ||
From the charge distribution, it is clear that the nitrogen centers are inherently very electron rich, and the boron are inherently extremely electron deficient, as expected. The nitrogen has the effect of withdrawing a lot of electron density from its hydrogen, while the boron has little effect. This explaines the difference in bond distance; this large difference in charge density in the NH bond will give it a small amount of ionic character.
The chlorine atoms are also effected by their adjoining atom, with those connected to boron being slightly electron rich, and those connected to the nitrogen being slightly electron poor. In the case of the N-Cl,this slight deficite may be due to the adjacent borons removing electron density from this nitrogen, and by proxy, the chlorine attached to it. The opposite is true for the B-Cl, with the adjacent nitrogens donating electron density through resonance.
This distriubution can be understood further by NBO analysis.
Firstly, the B-N bonds in the top half of the molecule: B-N(Cl)-B.
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
1. (1.98591) BD ( 1) N 1 - B 4
( 77.64%) 0.8812* N 1 s( 42.01%)p 1.38( 57.97%)d 0.00( 0.01%)
0.0001 -0.6482 -0.0027 -0.0005 -0.2821
0.0128 0.7071 -0.0067 0.0000 0.0000
0.0053 0.0000 0.0000 0.0042 0.0095
( 22.36%) 0.4728* B 4 s( 29.96%)p 2.33( 69.78%)d 0.01( 0.26%)
0.0004 -0.5468 0.0226 -0.0008 0.3973
0.0545 -0.7325 -0.0211 0.0000 0.0000
0.0365 0.0000 0.0000 0.0293 0.0209
2. (1.83735) BD ( 2) N 1 - B 4
( 89.73%) 0.9472* N 1 s( 0.00%)p 1.00(100.00%)d 0.00( 0.00%)
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.9999 0.0142
0.0000 0.0020 -0.0005 0.0000 0.0000
( 10.27%) 0.3205* B 4 s( 0.00%)p 1.00( 99.58%)d 0.00( 0.42%)
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.9979 -0.0059
0.0000 -0.0213 0.0615 0.0000 0.0000
It is clear that a vast majority of the bond density comes from the nitrogen; about 75% in the sigma bond and 90% in the pi. This shows the boron p in the conjugated plane is almost empty.
The N atom approaches sp hybridisation, while the B is approximately sp2. This is not the case throughout the molecule.
The remaing bonds can be represented using:
5. (1.97231) BD ( 1) N 2 - B 6
( 76.59%) 0.8752* N 2 s( 37.91%)p 1.64( 62.07%)d 0.00( 0.01%)
0.0001 -0.6157 -0.0015 0.0001 0.7852
-0.0079 -0.0623 -0.0149 0.0000 0.0000
0.0002 0.0000 0.0000 -0.0070 0.0088
( 23.41%) 0.4838* B 6 s( 31.31%)p 2.19( 68.45%)d 0.01( 0.24%)
0.0008 -0.5592 0.0188 -0.0041 -0.8247
-0.0406 0.0350 -0.0376 0.0000 0.0000
0.0084 0.0000 0.0000 -0.0437 0.0212
6. (1.82279) BD ( 2) N 2 - B 6
( 88.46%) 0.9405* N 2 s( 0.00%)p 1.00(100.00%)d 0.00( 0.00%)
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 1.0000 0.0027
0.0000 -0.0030 -0.0053 0.0000 0.0000
( 11.54%) 0.3397* B 6 s( 0.00%)p 1.00( 99.58%)d 0.00( 0.42%)
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.9976 -0.0260
0.0000 0.0633 -0.0123 0.0000 0.0000
The same contributions come from each atom, but the N now approaches sp2. The explains the "pinched" geometry, with B-N-B angles being slightly broader.
The N-Cl bond has a fairly balanced contribution from each atom, however the hybridisations are quite interesting.
4. (1.98756) BD ( 1) N 1 -Cl 9
( 55.99%) 0.7482* N 1 s( 15.92%)p 5.28( 83.97%)d 0.01( 0.11%)
0.0000 -0.3988 0.0105 0.0026 0.9164
0.0011 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 -0.0272 0.0198
( 44.01%) 0.6634*Cl 9 s( 10.95%)p 8.06( 88.21%)d 0.08( 0.85%)
0.0000 -0.0001 -0.3247 0.0633 -0.0001
-0.0001 -0.9374 0.0571 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 -0.0790 0.0473
The slight deficit in contribution from the chlorine agrees with its slight charge deficit. In this bond, both the N and the Cl are barely 'hybridised'; it is mostly a p-p bond.
Finally the B-Cl bond.
15. (1.99184) BD ( 1) B 7 -Cl 12
( 31.18%) 0.5584* B 7 s( 29.92%)p 2.33( 69.79%)d 0.01( 0.29%)
0.0005 -0.5467 0.0119 0.0123 -0.8353
-0.0123 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 -0.0480 0.0248
( 68.82%) 0.8296*Cl 12 s( 27.25%)p 2.66( 72.40%)d 0.01( 0.35%)
0.0000 -0.0001 -0.5219 -0.0116 -0.0008
0.0001 0.8508 -0.0125 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 -0.0517 0.0286
Over 2/3 of the charge density comes from Cl. The B appears almost sp2 hybridised, and the chlorine is almost sp3. It is clear that the ring induces different hybridisations in the two chlorine atoms which will make them react differently. If the B-Cl chlorine is sp3 hybridised, then it's bond will be stronger and its electrons lower in energy and less easily accessible. This agrees with the previous findings that the N-Cl* bond is in the LUMO and hence is more likely to react.
Chromium complex
There are several bonding interactions between the metal and the borazine ligand. However, it does seem as though they are made slightly akward by the symmetry of the borazine. The orbital below shows the interaction between the chromium s orbital; the only ideal alignment.
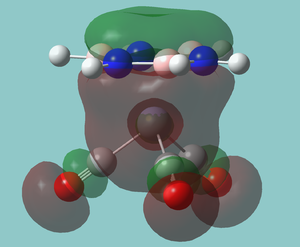
There is also an interesting low energy stablising interacting between the empty boron orbitals and the carbonyl pi bonds that still does not interact very strongly with the metal itself. The explains the preferences for the borazine ligand to orientate itself so that the borons are in line with the carbonyl group. This is also the interaction that explains all spectroscopic observations.
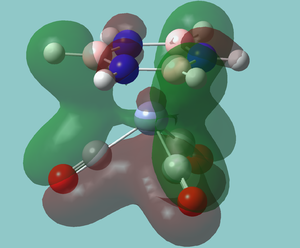
The effect of using chloro-substituted rings complex to metals could make interesting further study.