Rep:Mod:RM13Q4
Module 1
Computational Chemistry Module 1.

Using Molecular Mechanics to Predict Geometry and Regioselectivity
Molecular mechanics is a theory by which atoms in a molecule are treated purely classically. Every atom is defined as an exact point that can undergoe the typical laws of motion. By using this assumption, simple classical laws can be used to predict molecular behaviour without resorting to complex quantum analyses.
Using these calculations, the total absolute energy of a system can be determined, a quantity that is near impossible to determine experimentally. The energies that contribute to a molecule's total energy can be split into bonded and non-bondedfactors and is computed using the following classical equations.
Bonded Energy Terms
Hooke's Law descibes the force required to distort an object away from its equilibrium position, and can be used to describe both linear and angular distortions. The linear form is described as follows:
Where:
- F is the force exert on the object in an attempt restore it to the equilibrium position (where force is zero);
- x is the displacement from the equilibrium position and;
- k is the spring constant.
The angular form is identical, but with angular term:
Where:
- τ is the torque exert on the object in an attempt to restore it to the equilibrium position (where torque is zero);
- θ is the dispacement from the equilibrium angle and;
- κ is another spring constant.
By using the relationship between force and potential energy (shown below) it is possible to determine how much energy an object has in terms of of its position, x, and its angular distortion, θ from equilibrium. By following the potential energy surface, it is possible to find an energy minima.
Where:
- U(x) is the potential energy surface as a function of the variable x;
- F is the force experienced by the object at this variable x, given by the two equations above;
- U(x0) is the energy at the equilibrium postion (where force is zero, but energy may not be).
Hence, the following potential energy surfaces can be obtained:
A third equation that describes dihedral angles (an angle between two planes) is used in addition to these, which exhibits a cosine dependence. It describes the relationship between four bonded atoms and can help emperically model, for example, conjuagated systems in which adjacent alkenes will typically adopt a coplanar geometry.
With these equations, it is possible to calculate how much energy a certain configuration of atoms have relative to their equilibrium postion. Using the linear equation, bond lengths can be optimised, whilst the angular equation can optimise bond angles to the configuration where they experience no restoring force and hence have the lowest potential energy. When a component of a molecule cannot reach its equlibrium position because of other factors in the molecule, it remains in a higher energy state which contributes to the overall energy of the molecule. However, by being in this higher energy state, it may maximise a postive interaction else where in the molecule and lower the total energy of the molecule.
Non-bonded Energy Terms
A collection of atoms in space will not just experience each other through bonds, but will exert various other forces on each other.
Van der Waal's interactions are attractive forces that occur between atoms. They have an optimal distance at which the attraction is the strongest; the equilibrium position.
Where:
- V is the potential energy surface as a function of r;
- r is the radial distance between two atoms;
- σ is the equilibrium distance (essentially just a constant for the system) and;
- ε is another constant.
In MM2, this is split into "1,4" and "non-1,4" interactions, which simply means the calculation involves interactions of atoms 3 bonds apart, or more than 3 respectively.
The final interaction is the electrostatic interaction between dipoles. Dipoles are caused by electronegativity differences between atoms and can offer attractive or repulsive forces based on the strength and orientation of these dipoles.
The Total Energy
All the above factors are combined to give a total energy for the molecule. However, all these equations rely on empirical factors; none are from first principles. The reliance on empirical constants means that any "out of the ordinary" molecules cannot be predicted. And even for "simple" molecules, one constant may not be as accurate as it is for another.
This means molecular mechanics only allows the comparision between structures as the energies computed are nothing absolute. By applying the same equations to similar structures, any key factors that may result in a positive or negative energy difference can be observed and hence allow qualitative predictions. For quantitative predictions however, more sophisticated methods are required.
The Dimerisation and Hydrogenation of the Cyclopentadiene Dimer
Dimerisation
At room temperature, cyclopentadiene dimerises to form one of two isomers, the endo and the exo dimers in a typical Diels-Alder reaction[1] with one cyclcopentadiene unit acting as a diene, and another acting as the dienophile. For this reaction, there are two possible approaches:
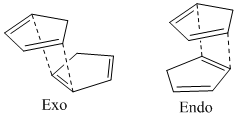
The endo has been seen to form preferentially[2].
By modelling both isomers, it is possible to determine which is the lowest energy form and predict which is the most thermodynamically stable product. This has been done using the MM2 system in ChemBio3D.
From these calculations, it can be seen that most energy contributions are very similar for each isomer. The largest difference is in torsion, which is to be expected. The bonds joining the cyclopentadiene rings are both gauche in the endo isomer, increasing the strain of the system relative to the two antiperiplanar conformations in the exo isomer.
This shows that the reaction cannot be under thermodynamic control as the higher energy isomer is formed. There must therefore be kinetic factors such as favorable interactions between molecular orbitals, a factor that effects the energy of the transition state of both reactions. This is not taken into account on any level in these calculations.
- ↑ Sauer, J.; Sustmann, R. Angewandte Chemie International Edition in English 1980, 19, 779-807.DOI:10.1002/anie.198007791
- ↑ Caramella, P.; Quadrelli, P.; Toma, L. Journal of the American Chemical Society 2002, 124, 1130-1131. DOI:10.1021/ja016622h
Hydrogenation
The cyclopentadiene dimer discussed above has two double bonds. When the molecule is hydrogenated, initially only one double bond is affected.
The two possible double bonds are shown below. One is on a bridged cyclopentadiene ring (left), while the other is not, giving them distinct environments.
 |
Using the same method as for the dimerisation, the thermodynamically favorable product can be predicted.
The two isomeric products are the result of the double bond in either the bridged or the un-bridged ring being hydrogenated.
| Hydrogenation of Bridged Ring | Hydrogenation of Un-bridged Ring | ||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
 |
| ||||||||||||||||||||||||||||||||
| Total Energy: 31.2 kcal/mol | Total Energy: 35.0 kcal/mol | ||||||||||||||||||||||||||||||||
|
|
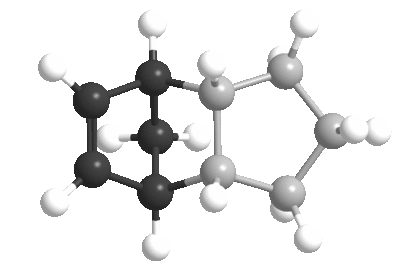
The bridged ring is shown in black and the double bond is always shown on the left .
It is clear that the major factor in the extra stability of the bridged ring hydrogenated product is due to the bending contribution. This logical, as the release of the strained ring (and hence strained bond angles) lowers the energy of this product considerably.
This product is also slightly favoured by 1,4 Van der Waal's interactions. These interactions are present in the region of double bond that was hydrogenated. The hydrogenated bridged ring is held in a slightly distorted configuration (but less distorted than the unhydrogenated compound) that holds the hydrogen atoms at a Van der Waal's attractive distance:
 |
However, the opposite product is favoured by non 1,4-Van der Waals interactions. This is because the curve in plane of this structure brings multiple hydrogen atoms together to an attractive distance.
 |
Torsion also favours this isomer because the double bond in the un-bridged ring imposes a greater restraint on the ring itself compared to the double bond in the bridged ring, where the double bond is in a position (the "base" of the pentagon) that on hydrogenation has little effect on the rings configuration. The larger change in the un-bridged ring allows the bonds connectting the rings to achieve a less distorted configuration.
| Bridged Ring Hydrogenation Product | Un-bridged Ring Hydrogenation Product |
|---|---|
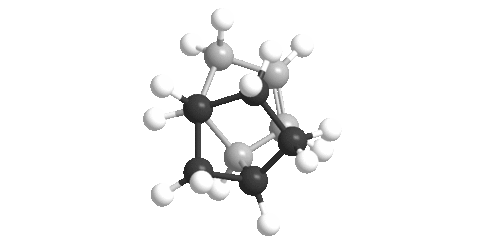 |
 |
The two images show the isomers looking down the inter-ring bond (left, central atom). On the left, it is clear that the bond is more eclipsed and is hence under more strain.
Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol
The studied compound herein is an intermediate in a complete synthesis of Taxol. It exists as various antropisomers because of restricted rotation around single bonds caused by the 9 membered cycle. In other words, the amount of energy required to move between these structures is appreciable relative to kT because, to "flip" the cyclohexane ring, it must also alter the configuration of the 9 membered ring; the two motions are dependant.
It can be made through an oxy cope reaction[1], shown below, in which it conforms to strict stereochemistry.
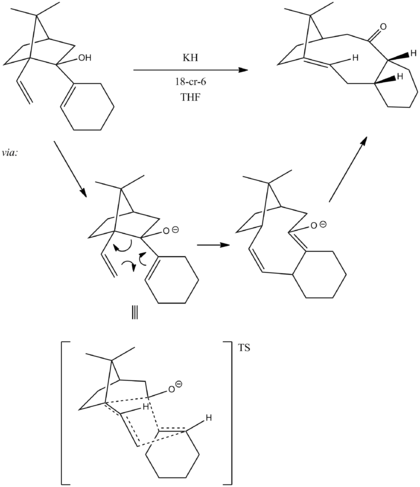
This is an example of an antropselective reaction. This selectivity can be explained by analysis of the transition state. Shown above, the reaction proceeds through a chair transition state to give specifically the up isomer (see below) and the correct stereochemistry of the alkene.
- ↑ Paquette, L. A.; Pegg, N. A.; Toops, D.; Maynard, G. D.; Rogers, R. D. J. Am. Chem. Soc. 1990, 112, 277-283 DOI:10.1021/ja00157a043
Up vs. Down
Below are two low energy antropisomers of this molecule: with the carbonyl either "up" or "down" relative to the cycohexane ring.
| Carbonyl "up" | Carbonyl "down" | ||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
 |
| ||||||||||||||||||||||||||||||||
| Total Energy: 47.8 kcal/mol | Total Energy: 42.7 kcal/mol | ||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
| Higher Energy Conformers | |||||||||||||||||||||||||||||||||
| Total Energy: 48.3 kcal/mol | Total Energy: 44.3 kcal/mol | ||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||
The two isomers shown come about from the different conformations of the cyclohexane ring with the carbon bearing the oxygen taking up either an axial or equatorial positions.
The predominant factor differentiating the "up" and "down" isomers is the bend energy contribution. The difference can be clearly seen in the carbonyl angles; the down isomer has ideal 120o angles while the carbonyl in the "down" isomer is considerably distorted.
| Up | Down |
|---|---|
 |

|
The down isomer also appears to have more favourable dipole/dipole attractions than in the up. The strongest dipole in both isomers is clearly the C=O bond, and by looking along this bond, it is clear why the down isomer is favoured. The two adjacent C-H bonds are almost anti-parallel with the carbonyl (with respect to carbon) in the down isomer.
In the C=O bond, the carbon is δ+ while in the C-H it is δ- due to the electronegativity differences between the elements. It aligns the C=O and two C-H bonds in the correct orientation for an attractive interaction, whereas there the up isomer has no such effect.
| Up | Down |
|---|---|
 |

|
The only relatively unfavourable energy contribution in the down isomer, and hence the only "expense" of taking up this configuration is torsional strain, and this is seen the the 6-membered ring as a result of a twist in the C-C(=O) bond.
| Torsion angles about carbon 1 | Torsion angles about carbon 2 |
|---|---|
 |

|
| Space filling model highlighting carbonyl trying to fit in cyclohexane ring | |
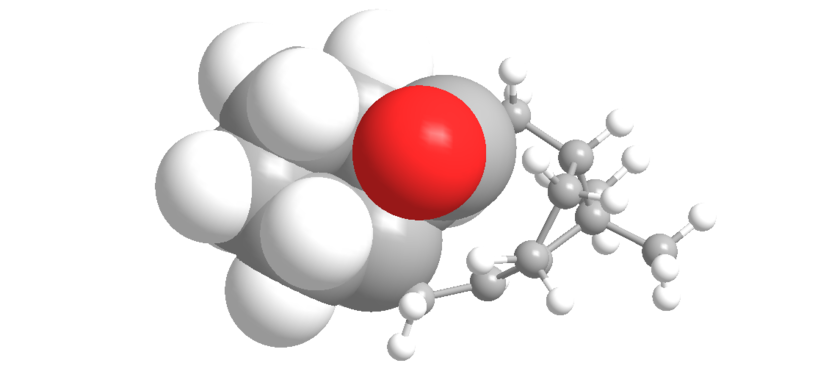
| |
This twist arises from the carbonyl having to fit in between the axial hydrogen of the cyclohexane ring as it itself is in an axial position. This twist distorts the torsion angles away from the ideal 60o increasing the energy of the down isomer. The up isomer places the equitorially and so the carbonyl points away from the ring, and hence does not experience this strain.
| Torsion angles about carbon 1 | Torsion angles abour carbon 2 |
|---|---|
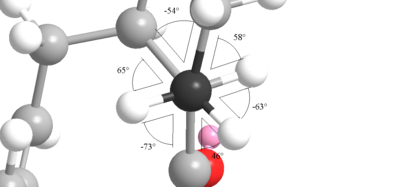 |

|
Despite the dihedral angles still looking fairly strined, an quick and simple analysis can show this is not the case:
| Up | Down | ||
|---|---|---|---|
| Angles About Carbon 1 (o) | Deviation from 60o(o) | Angles About Carbon 1 (o) | Deviation from 60o(o) |
| 46 | 14 | 49 | 11 |
| 54 | 6 | 49 | 11 |
| 58 | 2 | 50 | 10 |
| 63 | 3 | 66 | 6 |
| 65 | 5 | 67 | 7 |
| 73 | 13 | 79 | 19 |
| Angles About Carbon 2 (o) | Deviation from 60o(o) | Angles About Carbon 2 (o) | Deviation from 60o(o) |
| 52 | 8 | 44 | 16 |
| 53 | 7 | 47 | 13 |
| 56 | 4 | 52 | 8 |
| 59 | 1 | 68 | 8 |
| 65 | 5 | 69 | 9 |
| 75 | 15 | 79 | 19 |
| Total: | 83o | Total: | 137o |
| Deviation per bond | 6.9o | Deviation per bond | 11.4o |
There is almost twice as much deviation from ideality in the down isomer than there is in the up, clearly showing the increased torsional strain.
Comparison to MMFF94 analysis[1]
MMFF94 uses more complex and accurate estimates, and incorporates more physical effects than MM2. It generates more meaningful values such as the heat of formation, and can also be applied to larger systems such as proteins.
| Energy (kcal/mol) | ||
|---|---|---|
| Method | Up | Down |
| MM2 | 47.8 | 42.7 |
| MMFF94 | 70.6 | 60.7 |
The most noticable difference is that the values are much higher. This is because, as mentioned before, the it incorporates more physical effects (each with its own energy), all of which add up to a greater number. However, the most important factor to come from this is that both give the same isomer as the lower energy isomer. Also, the relative energy difference has increased by about 4%, indicating that the down isomer is more stable relatively then first calculated, and will exist in a greater proportion if left to equilibriate.
- ↑ Halgren, T. A. Journal of Computational Chemistry 1996, 17, 490-519 DOI:<490::AID-JCC1>3.0.CO;2-P 10.1002/(SICI)1096-987X(199604)17:5/6<490::AID-JCC1>3.0.CO;2-P
Implications on Stereochemistry
This antropisomerism (restricted rotation about a single bond)[1] has a large impact on stereochemistry. Depending on whether the molecule exists as the up or down isomer, the carbonyl will have opposite faces blocked. Hence, isomer the molecules exists in most (down) will give a dominant stereocentre.
| Up | Down |
|---|---|
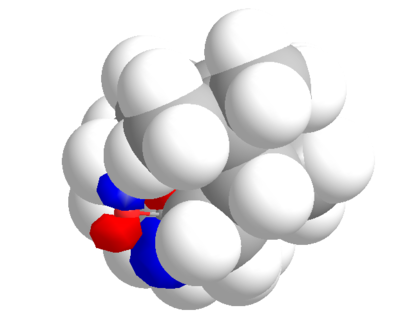 |

|
It is clear that only one face of the carbonyl is open to attack, and by inspection of both 3D models, these are opposing faces.
- ↑ Elmore, S. W.; Paquette, L. A. Tetrahedron Letters 1991, 32, 319-322 DOI:10.1016/S0040-4039(00)92617-0
Alkene Hyperstability
In general, alkenes are not thought to avoid taking up bridge head postions in bicyclic systems in accordances with Bredt's Rules [1]. However, as more and more examples where found, a more comprehensive way of predicting the likeliness of a bridgehead alkene forming was required. Many rules were made, but they were all general and always found their exceptions. However, on the advent of computational chemistry, it was found that it was possible to predict the stability of such alkenes using a quantity called "Olefinic Strain" [1].
The Olefinic Strain of a compound is found by subtracting the energy of the parent hydrocarbon of the alkene (essentially the hydrogenated product) and subtracting this from the energy of the alkene. Based on the outcome, it was possible to predict whether the resulting alkene was stable or not.
A similar calculation can be carried out on the taxol intermediate by "hydrogenating" the double bond (i.e. defining it as a single bond) and running the calculation.
| Alkene | Parent Hydrocarbon | Olefinic Strain (Difference) | |
|---|---|---|---|
| Energy (kcal/mol) | 42.7 | 49.4 | -6.7 |
In this case, the olefinic strain is negative. This means it falls into a class of "hyperstable" alkenes [2]. Due to the configuration of this alkene, there will be a large positive contribution to ΔG for its hydrogenation, which may over come the fact that two C-H bonds are more energetically favoured than a C=C double bond.
| Down isomer | Parent Hydrocarbon | ||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
 |
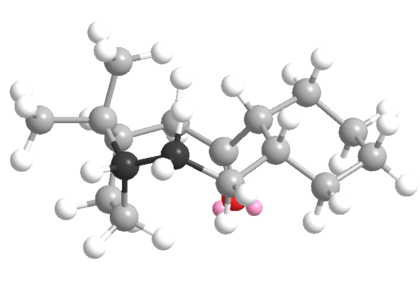
| ||||||||||||||||||||||||||||||||
| Total Energy: 42.7 kcal/mol | Total Energy: 49.4 kcal/mol | ||||||||||||||||||||||||||||||||
|
|
All but one energy contribution has become less favourable. The 1,4 Van der Waal's is more favourable for the parent hydrocarbon because the additional hydrogen are held at an attractive distance to their neighbours.
However, on hydrogenation, the structure takes on many unfavourable changes, who of which are shown below, namely the bend and the non-1,4 Van der Waals:
| Before | After |
|---|---|
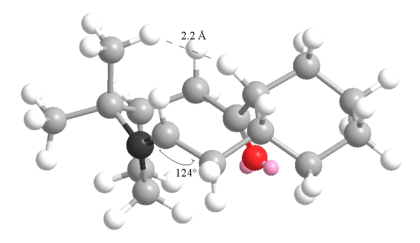 |
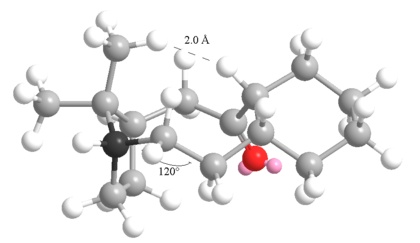
|
The highlighted carbon must now adopt a tetrahedral geometry that forces it "out" of the ring, twisting the pentagol ring towards the hexagonol. This bring two hydrogen too close together, and there held at a repulsive distance. The prevent them from getting closer still, the adjacent sp3 hybridised carbon must adopt a bond angle of 120o (shown), which increases the bend energy dramatically.
These factors make hydrogenation particularly slow for this compound.
- ↑ 1.0 1.1 Maier, W. F.; Rague Schleyer, P. von J. Am. Chem. Soc. 1981, 103, 1891-1900 DOI:10.1021/ja00398a003
- ↑ McEwen, A. B.; Rague Schleyer, P. von J. Am. Chem. Soc. 1986, 108, 3951-3960 DOI:10.1021/ja00274a016 10.1021/ja00274a016
Regioselective Addition of Dichloromethane
Molecular Orbital Explanation of Regioselectivity
Molecular mechanics does have its merits, but its inability to include electronic orbitals in its calculations means it is drastically incomplete. As shown above, it cannot explain the endo selectivity of the Diels-Alder reaction of cyclopentadiene.
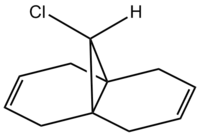
The following compound has two C=C double bonds, in fairly similar environments from a molecular mechanics point of view. However, electronically they differ greatly.
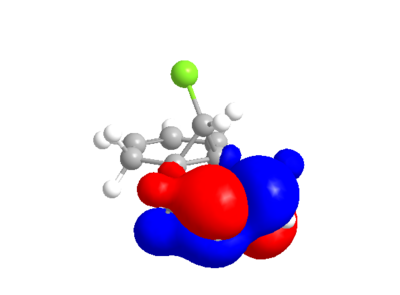
| HOMO | LUMO |
|---|---|
 |
|
| LUMO+1 | LUMO+2 |
 |

|
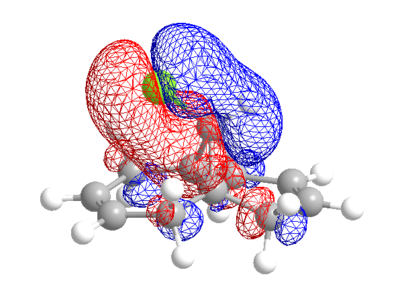 |
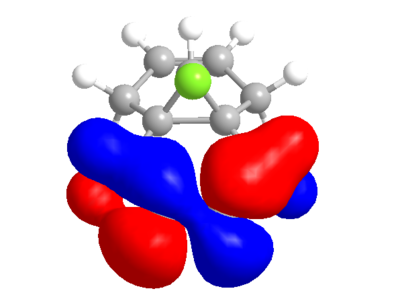
|
The calculated MO's from ChemBio3D are not quite symmetrical, particularly in the case of the LUMO and LUMO+2 where there is an odd "crossing over" of the "blue" phase. This may indicate that the structural optimisation is not perfect. Performing the same calculation and method in guassian gives the following orbitals, which for the most part are very similar, but actually conform with the symmetry of the molecule.
| HOMO | LUMO |
|---|---|
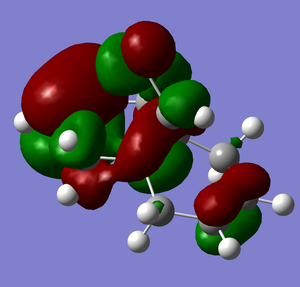 |
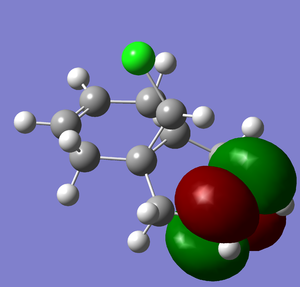
|
| LUMO+1 | LUMO+2 |
 |

|
From either MO calculation, it is clear the the two double bonds are not equivalent. The double bond on the side of the chlorine has substantial more electron density in HOMO than the other, making it more nucleophillic than the other, which is observed[3].
This other double bond has a slightly lower energy LUMO, and hence would be slightly more electrophillic (though this would depend on the hard/soft character of the incoming nucleophile).
- ↑ .out file of PM6 calculations
- ↑ .chk file of MO calculations
- ↑ B. Halton, S. G. G. Russell, J. Org. Chem., 1991, 56 (19), pp 5553–5556 DOI:10.1021/jo00019a015
Molecular Vibration Analysis (IR)
| C-Cl 930cm-1 | C=C 1737cm-1 | C=C 1757cm-1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
| |||||||||
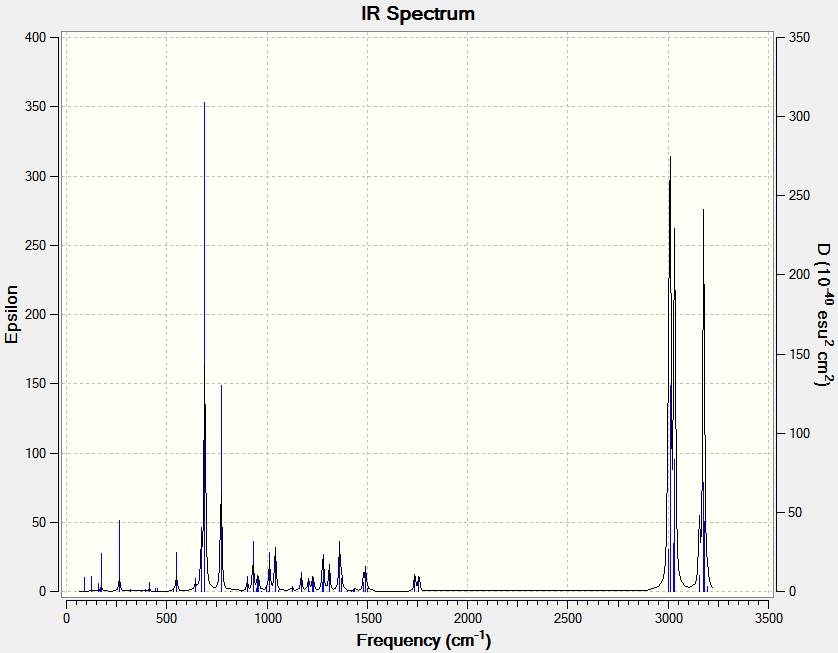
| |||||||||||
The syn double bond stretch is higher in energy as expected from the MO calculations. The HOMO showed a larger electron density on this bond, and hence it would experience a stronger restoring force (larger force constant, k in F=-kx) increasing its wavenumber.
| C-Cl 926cm-1 | C=C 1737cm-1 | ||||||
|---|---|---|---|---|---|---|---|
|
| ||||||
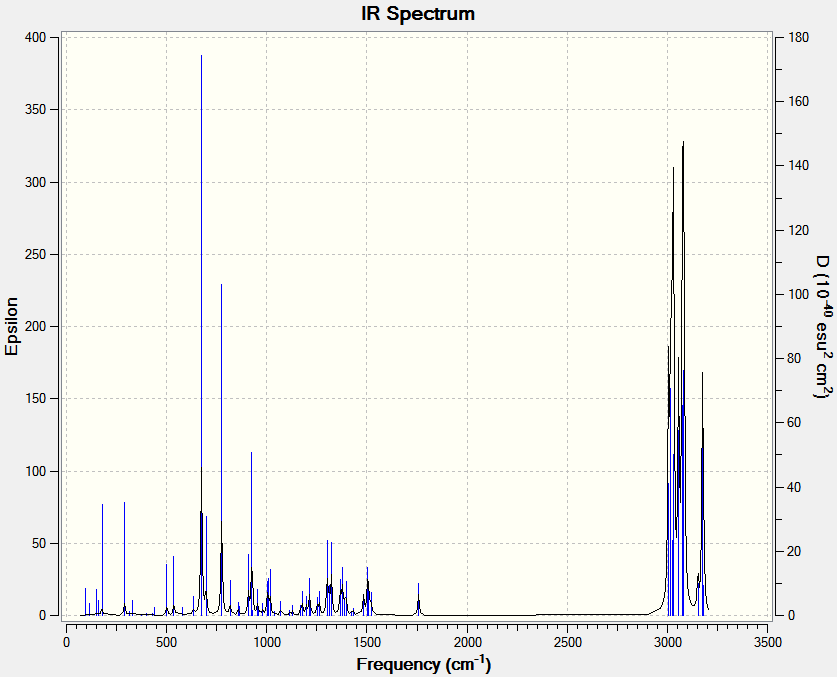
| |||||||
Each vibration experiences a decrease in wavenumber as the double bond is hydrogonated. This is because the distortion caused through out the molecule caused by each stretch has a large component in the double bond region. By replacing the double bond with a single bond, the motion in the molecule is less constrained and the vibration is lower in energy.
Another way of approaching this is by considering the vector of the chlorine molecule (which is not shown above as in the center of mass frame will be based around the chlorine). This vector should be balanced by other vectors within the molecule. In the unhydrogenated molecule, this is partly balanced by an out of plane wag of the anti alkene, which does not have ideal vector alignment and hence is quite large.
In the hydrogenated compound this position, which is now CH2 fragments can offset the C-Cl vector with a rock, which is both better aligned than the previous wag and rocks are also inherently lower in energy.
The same is true for the syn double bond; instead of the component on the opposite side of the molecule (small as it is, see diagram) being offset by a high energy C=C stretch in the unhydrogenated compound, it can be offset with much lower energy H-C-C-H bend in the hydrogenated compound.
- ↑ IR frequency calculation of unhydrogenated productDOI:10042/to-12810
- ↑ IR frequency calculation of hydrogenated productDOI:10042/to-12780
Monosaccharide Chemistry: Glycosidation
During glycosiation, sugars can take up various isomers, namely in the form of anomers. There are also conformational isomers within these definitions. These will be investigates using computational methods.
The reaction shown below can occur with various R groups.

For the purpose of computation, these will be assumed to be methyl groups as they will have little affect on the aspects of the sugars we are studying and they will reduce computational demand.
A & B
| Carbonyl Above | Carbonyl Below | ||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MM2 | |||||||||||||||||||||||||||||||||||||
 |

| ||||||||||||||||||||||||||||||||||||
| Total Energy: 20.0 kcal/mol | Total Energy: 14.1 kcal/mol | ||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||
| MOPAC/PM6 | |||||||||||||||||||||||||||||||||||||
| Heat of Formation: -85.0 kcal/mol [1] | Heat of Formation: -87.8 kcal/mol[2] | ||||||||||||||||||||||||||||||||||||
| The carbonyl moves below! | |||||||||||||||||||||||||||||||||||||
It is noted that the MOPAC/PM6 calculations move the carbonyl from above to below the plane compared to the MM2 calculations. The reason for this is clear on observation of the molecular orbitals:
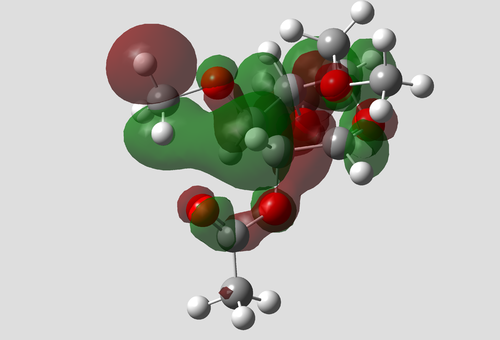 |
| Note: The acetyl is the bottom of the diagram and the red phase of the oxygen joins to the C-C bond. |
There is a clear pO to π*C=O interaction that would not have been incorporated in MM2 calculations.
A similar effect is present in down isomer, but it has larger implications
 |
 |
| Note: The acetyl is the bottom of the diagram and the green phase of the oxygen joins to the C-C bond. |
There is an appreciable interaction between the carbonyl O and the acylium C. This would be involved in no small degree with the neighbor group participation. ChemBio 3D gives it as HOMO -4, while Guassian HOMO -11. ChemBio models it as a pO to pCO, but interestingly, Guassian depicts what resembles a pO and pC sigma bond interaction.
The difference may be due to different levels of structure optimisation, but it does have real implications. It shows that it is possible to arrange the molecule from its ground state (assumed Guassian) to a distorted structure which brings the pO closer in energy to the acyllium antibonding orbital, allowing the reaction to occur.
There is also a notably large difference in what energy levels these orbitals occur in for both conformations. A (down) is in HOMO-11 while A (up) is in HOMO-5. This must be down to the fact that different oxygens in the acetyl group are interacting with the alkene. In A(up) it is the C-O-C oxygen, the interaction of which would be much more awkwardly alined than the C=O that interacts in A(down), leading to a strong interaction and hence lower energy. This shows that A(down) is the conformation that will go on to react.
These molecular orbitals would not be incorporated during MM2 at all, and in fact it would be difficult to predict a p-p sigma bond interacting with a lone pair on oxygen. For molecules in which MO's play a large role in the structure, MM2 cannot be used.
| Carbonyl Above | Carbonyl Below | ||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MM2 | |||||||||||||||||||||||||||||||||||||
 |

| ||||||||||||||||||||||||||||||||||||
| Total Energy: 10.6 kcal/mol | Total Energy: 12.4 kcal/mol | ||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||
| MOPAC/PM6 | |||||||||||||||||||||||||||||||||||||
| Heat of Formation: -88.5 kcal/Mol[5] | Heat of Formation: -75.4 kcal/Mol[6] | ||||||||||||||||||||||||||||||||||||
The energies calculated by both methods give the same conclusion; that the "up" isomer is the most stable. However, unlike for the A isomers, the B up isomer is considerably more stable than the down when calculated using MOPAC/PM6. This must be due to molecular orbital contributions.
 |
| This shows the 5 membered ring formed between the carbonyl being studied and the carbon of the acyllium component. The MO (green) is seen to link from the pO to the C-C(=O+) bond. |
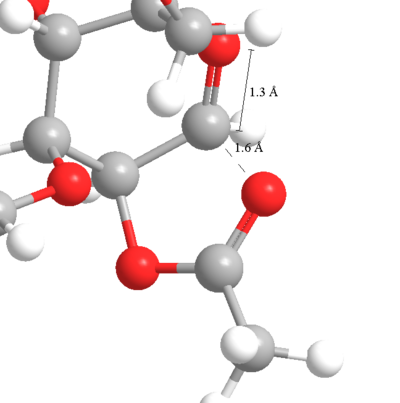 |
| This shows the 5 membered ring formed between the carbonyl being studied and the carbon of the acyllium component. The C...O distance is is comparable to the C=O distance. |
The B up isomer has similar to the A down that stablises this conformation. Once again, this could not have been predicted with MM2.
As noted above, MOPAC/PM6 gives a much larger difference in energies for the B isomers than it does for the A. This is purely due to molecular orbital contributions (as MM2 calculations do not give a difference this large), and it is likely that it is due to the "bonding" interaction between O..C=O+ being in a lower energy bonding MO for B than in A.
C & D
| C | D | ||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MM2 | |||||||||||||||||||||||||||||||||||||
 |
| ||||||||||||||||||||||||||||||||||||
| Total Energy: 26.8 kcal/mol | Total Energy: 28.0 kcal/mol | ||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||
| MOPAC/PM6 | |||||||||||||||||||||||||||||||||||||
| Heat of Formation: -91.7 kcal/mol [1] | Heat of Formation: -80.2 kcal/mol [2] | ||||||||||||||||||||||||||||||||||||
Implications on diastereospecificity
Based on the attained energies of formation from MOPAC/PM6, an estimate reaction profile can be made.

It can be seen that, even though A is higher in energy than B, once formed it can favourably form C, whereas A must undergo an endothermic reaction to form D. Therefore, under kinetic control, one would expect the β anomer (the less thermodynamically stable product) to form fastest because of the (presumably, Hammond's Postulate) large kinetic barrier of B to D.
The Total Synthesis of (-)Cubebol
Cubebol is an oil that is mainly used as a flavouring because it has a "cool" and "refreshing" taste[1]. It has several chiral centers centers. Two of these are found in the natural starting material (-)-menthone, whilst the others are invoked by an alcohol group, and the other two on the formation of a cyclopropane ring on the 6 membered ring.
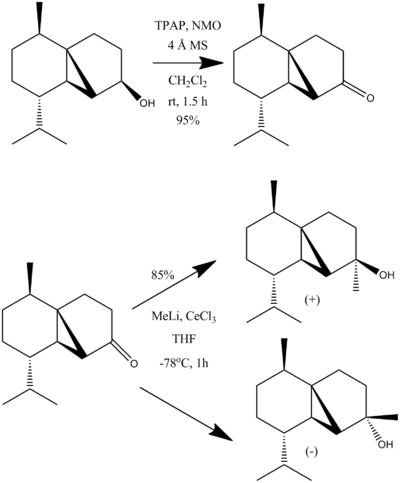
- ↑ Hodgson, D.; Salik, S.; Fox, D. J. J. Org. Chem., 2010, 75 (7), pp 2157–2168 DOI:10.1021/jo9022974
Isomers of Final Step
| (-)-cubebol | (+)-cubebol |
|---|---|
 |
|
| Heat of Formation: -81.3 kcal/mol[1] | "Heat of Formation: -81.5 kcal/mol[2] |
These energies are too similar for the selectivity to be explained thermodynamically as expected for enantiomers. These means this must be a kinetic phenomenon. Some TS analysis may be required.
C13 NMR
The model was optimised using PM6.
From literature[1]:
13CNMR(100 MHz) 80.3 (C-4), 44.1 (C-7), 39.0 (C-5), 36.3 (C-3), 33.6 (C-11), 33.4 (C-1), 31.7 (C-9), 30.8 (C-10), 29.5 (C-2), 27.9 (C-15), 26.4 (C-8), 22.6 (C-6), 20.1 (CMeMe), 19.6 (CMeMe), 18.7 (CHMe)
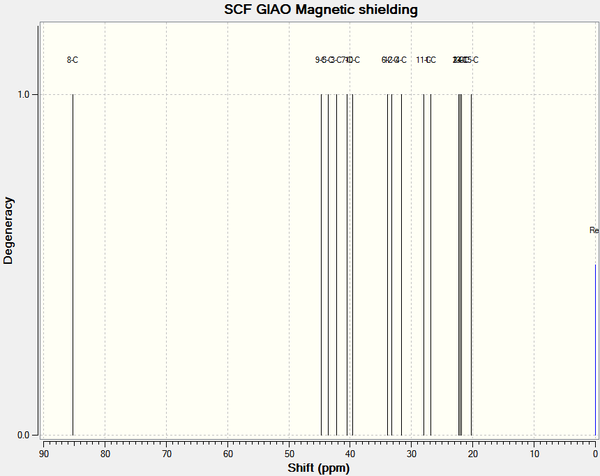
From calculation[2]:
# Summary of NMR spectra ( SCF GIAO Magnetic shielding)
# Values for element C only
# Reference: TMS mPW1PW91/aug-cc-pvdz CDCl3 GIAO
# Reference shielding: 193.86 ppm
# Degenerate peaks are condensed together (Degeneracy Tolerance 0.05)
#
# Shift (ppm) Degeneracy Atoms
80.8426000000 1.0000 8
41.7357000000 1.0000 9
40.3830000000 1.0000 5
39.5077000000 1.0000 3
36.7947000000 1.0000 7
36.6108000000 1.0000 10
31.4008000000 1.0000 6
30.7183000000 1.0000 12
28.4380000000 1.0000 4
27.7503000000 1.0000 11
24.3597000000 1.0000 1
19.6775000000 1.0000 2
19.5237000000 1.0000 13
19.1738000000 1.0000 14
17.8388000000 1.0000 15

By comparing the obtained shifts using the carbon allocations from the lit, the following deviations are obtained:


These deviations are substantial, and could indicate that an incorrect conformation has been simulated.
However, by simply comparing the shifts in numerical order, the following deviations are obtained:
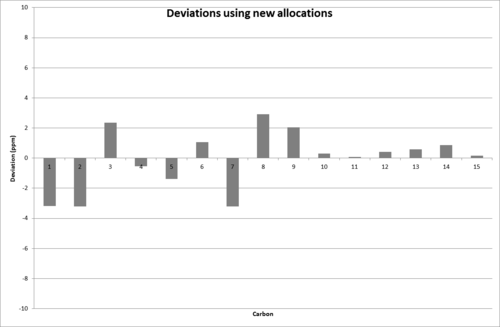
This gives the correct shifts within error. This may indicate that the literature allocations are wrong and the shifts actually correspond to:
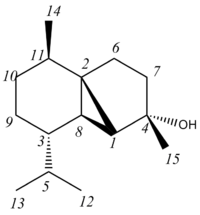
where the shift that was allocated previously retains its number and is shown on its new carbon.
- ↑ Hodgson, D.; Salik, S.; Fox, D. J. J. Org. Chem., 2010, 75 (7), pp 2157–2168 DOI:10.1021/jo9022974
- ↑ 13C NMR calculations using mpw1pw91/6-31(d,p) DOI:10042/to-12782
Comparison of (-) and (+) 13C NMR's and confirming formed isomer
| (-) |
|---|

|
| (+)[1] |
|
Lit 13C NMR
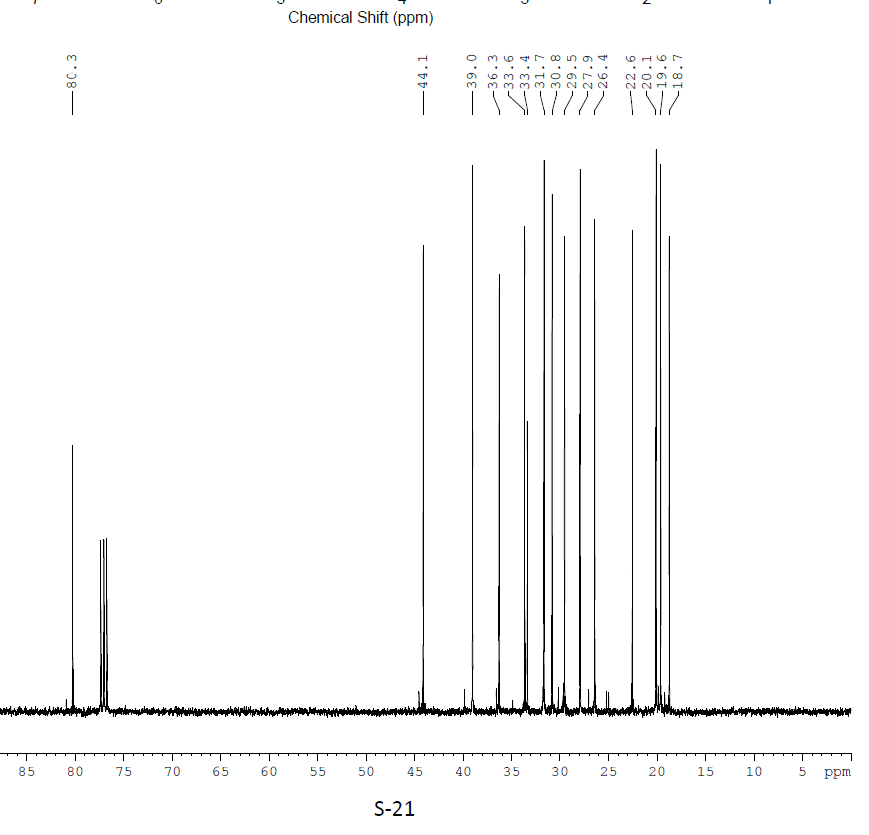
It can be seen that the (-) NMR appears closer in its pattern then the (+). Note the first few peaks from 45 ppm and lower. For example the pattern predicted: Peak, gap, peak, smaller gap, peak, gap, two very close peaks; is seen in the experimental NMR. The same is true for the whole spectrum.
Deviations for the (+) isomer from those obtained in lit.
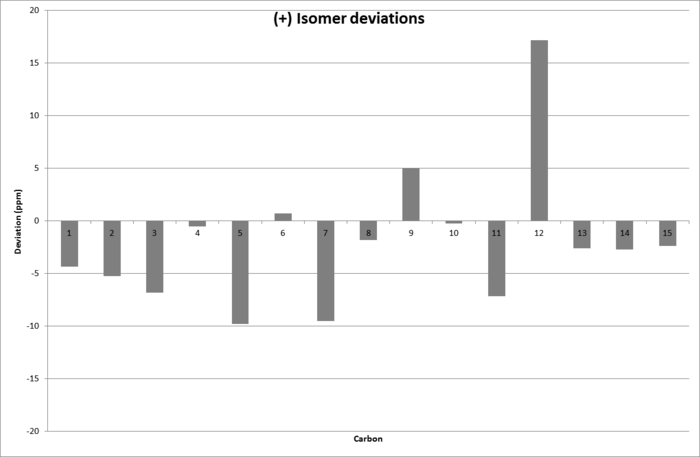
These are much greater than the ones for (-), one reaching as high as 17ppm deviation. This strongly supports that (-) has been synthesised.
- ↑ 13C NMR of (+)-Cubebol DOI:10042/to-12809
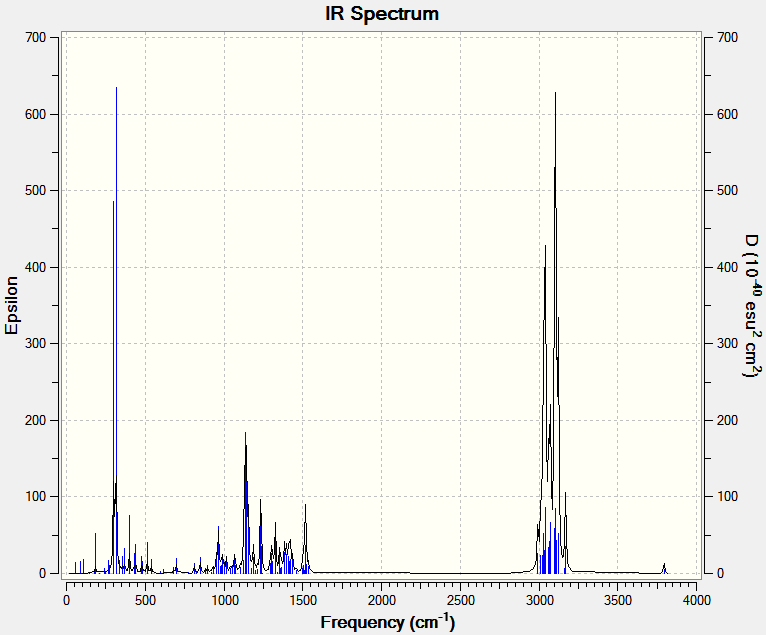
Infra Red Spectrum
The IR spectrum as calculated using # b3lyp/6-31G(d,p) opt freq [1]
3795 v(OH) (5)*
3105 v(CH) as in phase
3074 v(CH) as
2993 v(CH) (20,m)*
1506 (CH) scissoring
1500 (CH) scissor (2,w)*
1326 (CH) wag (24,m)*
1233 (CH) twist
1134 (OH) rock (?)
896 (CH) (2,w)*
315 (OH)
Lit. IR(cm-1) 3350 br, 2951 m, 2860 m, 1490 w, 1142 m, 910 w;
The starred peaks above are the closest to the found lit values. All apart from the OH agree with their relative intensities. The small predicted OH compared to experiment could be a sign of this models inability to incorporate bulk and intermolecular effects (H-bonding).
The IR spectrum of the (+) isomer will not give any discernible difference.
- ↑ IR for (-)-cubebol DOI:10042/to-12808
Optical Rotation
Computation still running, start time: 2012-03-01 10:45:35. If the result is negative, the proposed structure can be confirmed.
This may be quite a demanding process due to the many stereocenters.
Selective Epoxide Ring Opening
One stage in the synthesis of Cubebol is shown below.
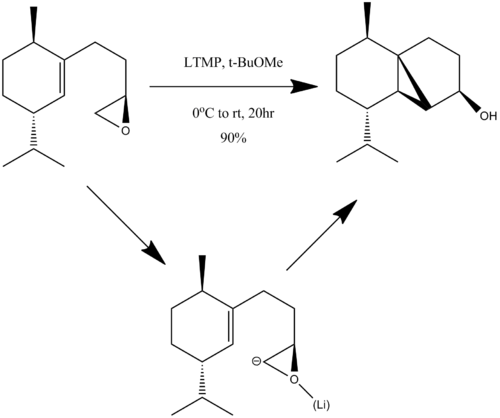
The epoxide can add on the top or bottom face of the alkene, yielding the product shown, or an isomer where the cyclopropane ring points "down".
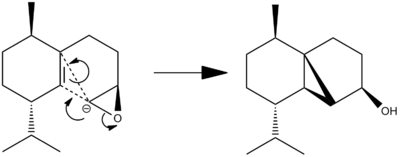
In this reaction, it is assumed the lithium binds to the oxygen facilitating the reaction. For the purpose of calculation, it will be assumed that the reaction precedes through the intermediate shown, essentially as if the epoxide was deprotonated with no lithium present. Attempting to model these yields some interesting results.
From the "arrow pushing" point of view, this is the best description of the reaction to occur once one of the following conformations is reached.
| MOPAC/PM6 | |
|---|---|
| Top Face | Bottom Face |
 |
|
| "Heat of Formation": -73.0 kcal/mol[1] | "Heat of formation": -32.9kcal/mol[2] |
| HOMO-2 of epoxide on top [3] | |||
|---|---|---|---|
 | |||
| This shows the atoms that form 5 member ring and the 3 member ring the product. It appears that the p orbital of the CH- fragenent is interacting with the antibonding orbital of the double bond. This may form the basis of the cyclopropane ring. | |||
| |||
| Note: Jmol has assumed the cyclpropane ring has formed due to the short distances involved. |
| HOMO-2 of epoxide on bottom [4] | |||
|---|---|---|---|
 | |||
| This shows the atoms that would potentially form the ring if the reaction proceeded. | |||
| |||
| Note: Jmol has assumed the ring has formed due to the short distances involved. |
| Top | Bottom | ||||||
|---|---|---|---|---|---|---|---|
 |
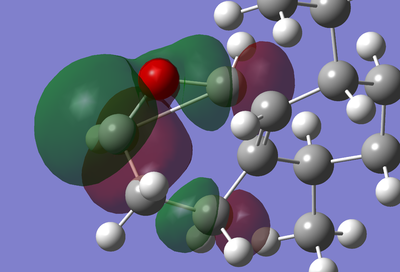 | ||||||
| The top attacking epoxide has a HOMO that is beginning to form a cylcic orbital, whereas the bottom attack HOMO does not. There seems to be no interaction with the alkene orbital. | |||||||
|
| ||||||
| Note: Jmol has assumed the rings has formed due to the short distances involved. | |||||||
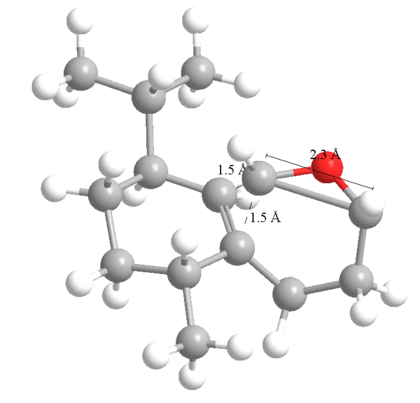
If attacking from the top face, calculations show an energy minimum with the C-O greatly extended, approaching a typical transition state (though this is not a transition state) for nuclephilic ring opening of epoxides[5].
If attacking from the bottom face, the C-C bond extends. This shows as long as the epoxide has the correct chirality, it cannot add on the bottom face because as it approaches, the MO's interact to break the "wrong" bond. In general, opening an epoxide to give the alcohol is much more favourable than ring opening the epoxide to give an ether.
Also the top "attack" conformation is much lower in energy than the bottom, presumably for the above reason. Hence, the molecule will spend far more time as the top than the bottom isomer (though there will be more stable isomers that will form the majority).
- ↑ PM6 optimsation of top face "attack"
- ↑ PM6 optimsation of bottom face "attack"
- ↑ .chk of Guassian for top "attack" is greater than 2MB and cannot be uploaded. Can send on request
- ↑ .chk of Guassian for bottom "attack"
- ↑ Harder, S.; Lenthe, J. H. van; Eikema Hommes, N. J. R. van; Schleyer,P. v. R. J. Am. Chem. Soc. 1994, 116 (6), pp 2508–2514 DOI:10.1021/ja00085a035