Rep:Mod:REF2496
Part 1: NH3 Molecule
The NH3 molecule was created and optimised using Gaussview, with summary information as follows:
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d.p) |
| Final Energy of the Molecule | -56.55776873au |
| RMS Gradient | 0.00000485 |
| Point Group | C3V |
The N-H bond length was determined to be 1.01798Å and the H-N-H bond angle 105.741°. The literature value of the bond length for ammonia is 1.012Å, and the bond angle is 106.7°.[1] Comparing the values obtained from the optimisation to the literature values, the experimental values are slightly less. The bond angle for ammonia is less than what is expected from a tetrahedral molecule due to the electron repulsion between the lone pair on the nitrogen atom and the bonding electron pairs.
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000070 0.001800 YES
RMS Displacement 0.000033 0.001200 YES
Predicted change in Energy=-5.785171D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7412 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7412 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7412 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.8571 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Optimised NH3 Molecule |
The link to the optimised NH3 log file can be found here.
Frequency and Charge Analysis of NH3 Molecule
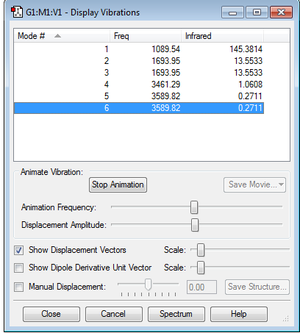
From the 3N-6 rule there are 6 modes of vibrations that are expected, where N is the number of molecules and is equal to 4 for NH3. Figure 1 shows that 4 modes are degenerate as they have the same frequency; modes 2 and 3 at 1693.95cm-1 , and modes 5 and 6 at 3589.82cm-1 . Modes 1, 2 and 3 are bond bending vibrations, and modes 4, 5 and 6 are bond stretching vibrations. Both modes 1 and 4 are both highly symmetric, however mode 4 is the most symmetric of the two modes, and mode 1 is known as the "umbrella" mode. In an experimental spectrum of gaseous ammonia, it is expected that there will be 2 observable bands. Mode 1 gives a very large intensity peak in comparison to the other modes, and hence only this peak and a peak for modes 2 and 3 will be observable on the spectrum.
The charge of the nitrogen atom is -1.125 and the charges on each of the 3 hydrogen atoms is +0.375. The charge of the nitrogen atom would be expected to be negative, and the charge of each hydrogen atom expected to be positive as nitrogen is much more electronegative than hydrogen, and hence the electron density from the hydrogen atoms is drawn towards the nitrogen atom.
N2 Molecule
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d.p) |
| Final Energy of the Molecule | -109.52412868au |
| RMS Gradient | 0.0000006 |
| Point Group | D∞h |
The N-N bond length obtained is 1.10550Å, comparing this to the literature value of 1.0975Å,[2] it is apparent the experimental value from the optimised structure is greater than the literature value.
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.383595D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1055 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Optimised N2 Molecule |
The link to the optimised N2 log file can be found here.
There is only one mode of frequency for the N2 molecule, with a corresponding frequency of 2457.33cm-1, hence there are no negative frequencies.
H2 Molecule
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d.p) |
| Final Energy of the Molecule | -1.17853936au |
| RMS Gradient | 0.00000017 |
| Point Group | D∞h |
The H-H bond length is 0.74279Å. The literature value of the H-H bond length is 0.74Å[3], which is very similar to the experimental value obtained from optimisation.
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.167770D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.7428 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Optimised H2 Molecule |
The link to the optimised log file for H2 is here.
There is only one mode of frequency for the H2 molecule, at a frequency of 4465.68cm-1, hence there are also negative frequencies.
Reaction Energies of NH3
Reaction: N2 + 3H2 → 2NH3
| E(NH3) | -56.55776873au |
| 2 x E(NH3) | -113.1155372au |
| E(N2) | -109.52412868au |
| E(H2) | -1.17853936au |
| 3 x E(H2) | -3.53561808au |
ΔE = 2 x E(NH3) - [E(N2) + 3 x E(H2)]
ΔE = -0.05579044au
ΔE = -0.05579044 x 2625.5
ΔE = -146.48 kJmol-1
The energy for converting hydrogen and nitrogen gas into ammonia gas is equal to ΔE = -146.48 kJmol-1. The energy change for this reaction is negative, indicating an exothermic reaction where energy is released to obtain the product. Hence the ammonia product is more stable as it is lower in energy than the gaseous reactants.
The literature value of the enthalpy of formation of ammonia, NH3, is -45.90kJmol-1.[4] The reaction above produces 2 moles of ammonia, hence the literature enthalpy change for the above reaction is -91.80kJmol-1. This value is significantly smaller than the experimental value obtained.
Part 2: Choice of Small Molecule - H2SiO
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d.p) |
| Final Energy of the Molecule | -365.90001403au |
| RMS Gradient | 0.00000941 |
| Point Group | Cs |
The Si-H bond length was determined to be 1.48652Å, and the Si-O bond length to be 1.53172Å. The H-O-H bond angle is 54.933°, and both H-H-O and O-H-H angles are 62.533°. The H-Si-O angles are 124.158° and 124.156° (with each hydrogen 1 and 2). The literature bond length of Si-H is 1.509Å and 1.507Å between each hydrogen, which is greater than the values obtained. The literature value for the Si-O bond length is 1.552Å, slightly less than the values calculated from the optimisation. The literature value of H-Si-O bond angle is 124.0° and 123.4° (with each hydrogen 1 and 2), which is very similar to the values obtained. However, for the angles corresponding to each of the different hydrogens, the difference in the optimised experimental results is significantly smaller than the difference between the two literature values. [5]
Item Value Threshold Converged?
Maximum Force 0.000023 0.000450 YES
RMS Force 0.000009 0.000300 YES
Maximum Displacement 0.000024 0.001800 YES
RMS Displacement 0.000018 0.001200 YES
Predicted change in Energy=-5.357811D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.4865 -DE/DX = 0.0 !
! R2 R(1,3) 1.4865 -DE/DX = 0.0 !
! R3 R(1,4) 1.5317 -DE/DX = 0.0 !
! A1 A(2,1,3) 111.686 -DE/DX = 0.0 !
! A2 A(2,1,4) 124.1565 -DE/DX = 0.0 !
! A3 A(3,1,4) 124.1576 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Optimised H2SiO Molecule |
The link to the optimised H2SiO log file can be found here.
Frequency and Charge Analysis of H2SiO Molecule
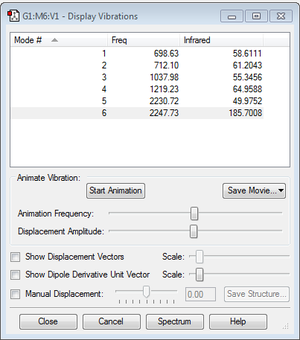
From the 3N-6 rule, where N is the number of atoms, the expected number of nodes is 6, which is also the observed number as seen in Figure 2. Modes 1 and 2 are bond bending vibrations and modes 3-4 are bond stretching vibrations. There are also no degenerate modes, and no negative frequencies. Mode 5 is highly symmetric and Mode 1 is known as the 'umbrella' mode. In an experimental spectrum of H2SiO, the number of observable bands is expected to be 6 peaks, representing modes 1-6. The intensities of all of the peaks are high enough in comparison to each other to be observable on the spectrum. However, Modes 5 and 6 have very similar frequencies; 2230.72-1 and 2247.73-1, respectively. The intensity of Mode 5 is significantly less then Mode 6, hence the peaks for Modes 5 and 6 appear slightly less defined compared to each other as they are very close together.
The charge of the silicon atom is +1.472, the charge of the oxygen atom is -1.001 and the charges of the hydrogen atoms is -0.235. The charge of the oxygen atom would be expected to be negative as it is highly electronegative in comparison to both hydrogen and silicon, hence attracts the majority of the electron density. As a direct result of this, silicon is expected to have a positive charge and this causes hydrogen to have a negative charge also. Hydrogen is also slightly more electronegative than silicon, however the magnitude of the charge is less than the charge for oxygen as this difference is comparatively small.
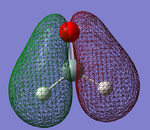
Molecular Orbitals of H2SiO
Molecular Orbital 1
Figure 3 shows a bonding molecular orbital that is occupied. The atomic orbitals it is constituted from are the 1s orbital of the hydrogens and the 2p orbital of the oxygen. It is the corresponding bonding orbital to the anti-bonding orbital (Molecular Orbital 2), displayed in Figure 4. This MO is low in energy, with an energy of -0.39697, and will stabilise the bonding in the molecule.

Molecular Orbital 2
Figure 4 shows another of the molecular orbitals of H2SiO. This MO is occupied, and shows anti-bonding. The contributing atomic orbitals are the hydrogen 1s and the oxygen 2p orbitals. The energy of this orbital is -0.28497, and represents the HOMO, the molecular orbital with the highest energy that is occupied. As this MO is occupied and has anti-bonding, it will hence weaken the bonding over the molecule.

Molecular Orbital 3
Another molecular orbital of H2SiO is displayed in Figure 5. This molecular orbital is occupied and shows pi bonding, and is the corresponding bonding orbital to the anti-bonding orbital (MO 4), as shown in Figure 6. The atomic orbitals that contribute to this particular molecular orbital are the oxygen 2p orbital and the silicon 3p orbital. The molecular orbital is in the HOMO region and has an energy of -0.31773. This MO will also stabilise the bonding across the molecule.

Molecular Orbital 4
The molecular orbital as displayed in Figure 6 shows pi-antibonding (π* orbital), and is unoccupied. The orbital is constituted from the oxygen 2p orbital and the silicon 3p orbital, and is the corresponding anti-bonding orbital of Molecular Orbital 3, as displayed in Figure 5. This MO has an energy of -0.07728, and is the LUMO, the molecular orbital with the lowest energy that is unoccupied. The anti-bonding in this MO will also slightly weaken the bonding over the molecule.

Molecular Orbital 5
Figure 7 shows an occupied molecular orbital of H2SiO which has both bonding and anti-bonding. The lower red molecular orbital shows σ bonding between the 1s atomic orbitals in each hydrogen atom. The higher red and green MO shows anti-bonding between the oxygen 2p and the silicon 2p orbitals. The energy of this MO is -0.35346, hence it is low in energy and very stable. Since σ bonds are the most stable, this will stabilise the positions of the hydrogen atoms.
References
- ↑ CRC Handbook of Chemistry and Physics, 94th ed. http://www.hbcpnetbase.com. Page 9-26. Retrieved 18 June 2013.
- ↑ http://www.wiredchemist.com/chemistry/data/nitrogen-compounds
- ↑ http://www.chem.tamu.edu/rgroup/connell/linkfiles/bonds.pdf
- ↑ Chase, M.W., Jr., NIST-JANAF Themochemical Tables, Fourth Edition, J. Phys. Chem. Ref. Data, Monograph 9, 1998, 1-1951. [all data]
- ↑ http://www.colby.edu/chemistry/webmo/H2SiO.html
