Rep:Mod:Pterodactyladiene

Sergei Palmer Year 3 Computational Labs - Module 1: Symmetry and Spectroscopy

Modelling using Molecular Mechanics

MM2 is a second generation classical force field which can be used to describe and quantise the energy of a molecule. Generally the functions and parameters for a force field are derived using both experimental and quantum mechanical computational work. MM2 is the first in a series of modelling packages developed by Norman Allinger. They are fairly basic in that they use Newtonian mechanics for the modelling calculations, essentially treating a molecule as a series of balls and springs.

The Hydrogenation of Cyclopentadiene Dimer

Endo vs Exo Selectivity in the dimerisation

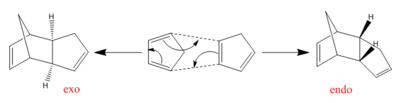
Cyclopentadiene is an organic compound used mainly for the production of cyclopentenes. It also has an important role in organometallic chemistry as it is the precursor in the formation of the cyclopentadienyl (Cp) ligand. One of the most famous Cp-ligand containing complexes is Ferrocene, a sandwich compound, whose structure was first deduced by Woodward and Wilkinson in 1952.At room temperature, cyclopentadiene will dimerise via a _π4_s + _π2_s Diels-Alder cycloaddition reaction in which the dimer has been found to prefer the kinetic, endo form over the thermodynamic, exo form.^,

Figure 1 - Cyclopentadiene dimerisation to dicyclopentadiene

Figure 2 - 1. Exo Dimer 2. Endo Dimer 3. Hydrogenated Endo Dimer 1 4. Hydrogenated Endo Dimer 2

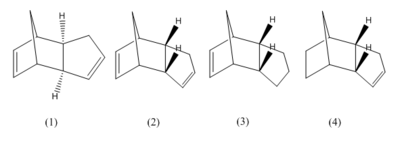
Using MM2 molecular modelling techniques built into ChemBio3D (v. 12.0.2), the dimerisation reaction was investigated by optimising the geometry of the (exo) and endo (2) forms as well as two products obtained by hydrogenating the endo dimer (3 & 4). From this, the relative stabilities, the bond strain [using bond stretches, bends, torsion energies and dihedral angles (for 1 & 2)] and bond angles (for 3 & 4) can be determined.

Table 1 - Cyclopentadiene MM2 Calculation Results (all energies in kcal/mol)

Molecule	Stretch	Bend	Stretch-Bend	Torsion	Non-1,4 VDV	1,4 VDW	Dipole/Dipole	Total Energy
	1.285	20.580	-0.838	7.656	-1.417	4.233	0.378	31.876
	1.251	20.848	-0.836	9.511	-1.544	4.320	0.448	33.998
	1.278	19.859	-0.835	10.811	-1.223	5.633	0.162	35.685
	1.097	14.524	-0.549	12.498	-1.070	4.513	0.141	31.152

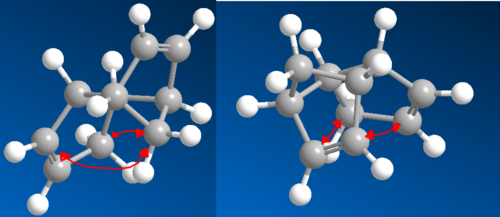
From the table, it is possible to see that that the exo-form is more stable than the endo-form by 1.462 kcal/mol. The component most responsible for this is the torsional energy with a difference of 1.855 kcal/mol between the endo- and exo-form. As explained in the molecular mechanics wiki page, the torsion energy is the sum of of all tetra-atomic bond torsions. Comparing fig. 3 with fig. 4, the differences between the two can be observed. In the exo-form, there is only 1,4 one torsional interaction as both of the two available carbons on the cyclopentadiene ring interact with the bridging carbon on the norbornene ring. However in comparison, in the endo form, the norbornene ring is now facing the cyclopentadiene ring meaning there are two different carbons which can be interacted with, not just one. Sterically this makes the exo-form the more stable of the two which explains the highter energy associated with the endo-form bond torsion. Aside from this, the other energy components are very similar and don't impact as greatly. Hence It is necessary to determine under what control the reaction proceeds.

Figure 3 - Left - Bond Torsion in exo-form --- Right - Bond Torsion in endo-form

The kinetic product is that which forms more quickly whilst the thermodynamic product is the one which is more stable. From the MM2 results obtained, this would suggest that the exo-dimer is produced under thermodynamic control whilst the endo-form would be produced more quickly under kinetic control. As the endo-dimer is formed preferentially, the dimerisation of cyclopentadiene is kinetically controlled. Although less stable, this product is preferred in irreversible Diels-Alder reactions.

Fig. 4 shows a frontier molecular orbital approach to the bonding of the endo-form using the LUMO of diene A with the HOMO (ψ₂) of diene B. This is the correct symmetry arrangement for bonding interactions to occur as there is a node in the middle of both the LUMO of A and HOMO of B. The opposite arrangement taking the HOMO of A and the LUMO of B would also work. Either would work fine, though as most Diels-Alder reactions involve electron-rich dienes with electron-poor dienophiles, the first arrangement is preferred as it results in a better overlap in the transition state.

Figure 4 - Diagram showing the formation of the endo product

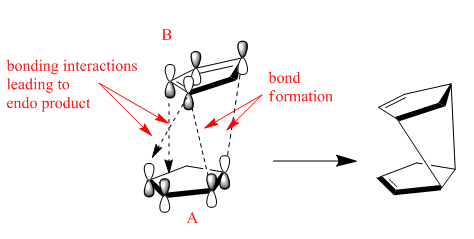
This is because of the high-energy of the HOMO (B) and the low energy of the LUMO (A) resulting in a small energy gap, hence the strong overlap. Furthermore, the symmetry at the back of A is also correct for a bonding interaction. Although no bonds are actually formed from this interaction, it affects the stereochemistry of the product favouring the endo product due to the favourable through space interaction between the orbitals.

Endo hydrogenation products

When comparing the two products obtained by hydrogenating the endo-form, it is clear that 4 is more stable than 3 by 4.533 kcal/mol. The largest component of this difference is the bend energy with 3 being higher by 5.335 kcal/mol. This is made up of the sum of the sum of all triatomic bond angle deformations. Hence by looking at the bond angles of the double bonds within each product, it is possible to demonstrate this discrepancy. Each carbon in a double bond is sp² hybridised meaning that the ideal bond angle is approximately 120°. Thus the more the bond angle in the dimer deviates from ideality, the higher the strain within the ring and so the less stable the molecule. Product 3 has a bond angle of 107.8° compared with an average of 112.7° in product 4. This difference correlates with the MM2 calculation data showing 4 to be more stable than 3 and it has been shown that this can be illustrated by the difference in bond angle and hence ring strain. Hence it would be expected that that product 4 (thermodynamic product) would be formed due to its higher stability. Experimentally, it has been found that this is indeed the case and the norbornene is the one which will be hydrogenated first. However, we cannot definitively say under what control the reaction proceeds from the information available due to the limitations of the MM2 modelling technique. The frontier molecular orbitals would need to be considered which is something this relatively primitive modelling allows for.

Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

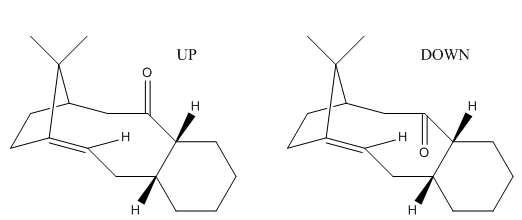
Taxol (also known as paclitaxel) is an important drug used to treat patients with many types of cancer including lung, ovarian and breast. An important intermediate in its synthesis, as proposed by Paquette in 1991, can either form with the carbonyl group pointing up (F) or down (G). On standing, the compound isomerises to the alternate form. This is an example of atropisomerism which generally occurs when there is restricted rotation about a single bond as a result of high steric hinderance removing the ability to freely rotate. In the taxol precursors, the issue is found to "originate in the restricted rotation of substituted aromatic rings within macrocyclic structures".

Modelling Results

First of all, MM2 modelling was used to determine which was the more stable atropisomer. For comparison, the minimisation was also done with MMFF94,a force field developed by Merck, based on the MM3 force field.

Modelling Data	Taxol intermediate structures
Table 2 - Taxol intermediates MM2 & MMFF94 Calculation Results (all energies in kcal/mol) Molecule Stretch Bend Stretch-Bend Torsion Non - 1, 4 VDW 1, 4 VDW Dipole/Dipole Total Energy (MM2) Total Energy (MMFF94) 2.785 16.541 0.430 18.251 -1.552 13.109 -1.725 47.840 70.528 2.621 11.339 0.343 19.672 -2.162 12.872 -2.002 42.683 60.545	Figure 5 - Possible Taxol synthesis intermediates

Although it is not possible to directly compare the MM2 energies with those calculated using MMFF94, the relative energies between the two can be looked at. As can be seen in table 2, G was determined to be the more stable intermediate as shown by its lower energy calculated by both force fields. Additionally, looking at the geometries, it is possible to see that, as expected, the chair conformation for the cyclohexane ring is preferred in both atropisomers as it is known to be the lowest energy conformer of cyclohexane. F is the kinetic product and will be formed fastest in the reaction, and hence would be expected to have a less energetic transition state. Transition states cannot be modelled using these basic force fields as they are based on classical mechanics and so calculating frontier molecular orbitals to confirm this is beyond these simpler modelling techniques. If the individual components of the calculated intermediate energies are compared, it is clear that the bend energy is responsible for the largest discrepency between F & G with a difference of 5.202 kcal/mol; this indicates that there is more ring strain when the carbonyl group is up rather than down.

Hyperstable olefins

In 1924, Bredt noted that olefinic bonds had a tendency to avoid ring junctions in larger cyclic systems due to high ring strain occuring from a combination of the associated double bond strain and residual strain from the carbon skeleton. From this arose the use of OS (olefinic stability) as an index of bridgehead stability. It is calculated by subtractng the total strain of the most stable conformer of the parent hydrocarbon from the total strain of the olefinic compound. However what Maier and von Ragué Schleyer found was that some sets of compounds gave a negative OS value, which were termed hyperstable olefins. This concept was applied to the most stable conformation which determined above (G) and compared to its parent hydrocarbon (). Its energy was minimised using MM2 and found to be 52.897 kcal/mol, giving an OS of -10.214 kcal/mol. This confirms that G is a hyperstable olefin and hence more stable than its saturated parent. As a result, it is expected that G will be quite unreactive as it is stabilised due to the location of its double bond at a bridgehead. Clearly, losing this extra stability would require substantial energy to be put into the system in order to overcome the activation barrier to break this bond.

Modelling using Semi-empirical Molecular Orbital Theory

In this section, the calculations will be performed with the more advanced PM6/MOPAC modelling technique.

By going from MM2 to PM6 modelling, it is possible to show the transition from a purely classical mechanical treatment of a molecular into a more quantum mechanical one which takes electron wave-descriptions into account. This will help to illustrate the weaknesses of MM2 as a technique in looking into the more complex orbital interactions which it can't handle.

Regioselective Addition of Dichlorocarbene

Dichlorocarbene is an electrophilic reagent which can react with alkenes to form geminal dichlorocyclo- systems in a [1+2] cycloaddition reaction. Fig. 6 shows the reaction with K, which can be used to demonstrate the control that orbitals have over reactivity.

Figure 6 - Reaction of Dichlorocarbene with K

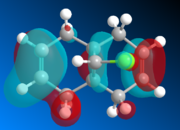
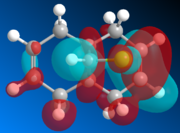
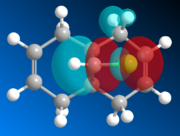
The geometry of K is modeled initially using MM2 and followed by the more advanced PM6 method to determine the orbital energies and then display their forms visually. In part one, the structure of K will be investigated with MM2 and PM6 in order to provide an approximation of the valence-electron molecular wavefunctions, paying particular attention to the HOMO. It it presumed to be the most reactive with regards to electrophilic attack, and so using PM6, the two alkene bonds can be distinguished to work out which one is more nucleophilic.

Table 3 - HOMOs and LUMOs for Product K calculated using PM6

HOMO-1	HOMO	LUMO	LUMO+1	LUMO+2

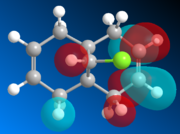Looking at the calculated MOs, it is clear to see that the HOMO has the majority of its electron density centred over the endo double bond (i.e. on the same side as the chlorine). This makes it far more nucleophilic than the exo double bond and so more susceptible to electrophilic attack. The LUMO on the other hand has its electron density over the exo double bond in the π-antibonding orbital. Therefore it will be more likely to undergo reactions with nucleophiles. In the reaction scheme in fig. 6, the electrophilic dichlorocarbene is shown attacking the endo double bond. As the frontier MO calculations have now shown, this is indeed how the reaction would be most likely to occur.

Following this, product K and its monoalkene derivative (L, see fig. 7) were optimised using Gaussian [(B3LYP/6-31G(d,p)] and then their IR spectra predicted and analysed to see if the two can be distinguished. For K, it is expected that there will be two olefinic stretches, one for each double bond. Additionally, a C-Cl stretch should appear between 750-850cm^-1 It should be possible to identify the dihydro derivative as in its IR spectrum, the loss of the exo C=C stretch should be observed.

Figure 7 - K dihydro derivative, L

Table 4 - IR spectra for K and its dihydro derivative, L

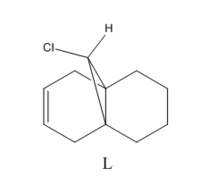
Molecule	Spectrum	URI
K		DOI:10042/to-10376
L		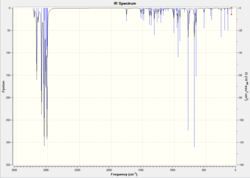DOI:10042/to-10398

Table 5 - IR stretch identification

K - Stretch animation	Stretch (cm-1)	L - Stretch animation	Stretch (cm-1)
	C-Cl - 770.85		C-Cl - 780.03
	C=C (exo) - 1737.04	N/A	N/A
	C=C (endo) - 1757.35		C=C (endo) - 1753.72

The IR spectra can also be used to illustrate the difference in C-Cl bond strength between the two molecules. The hydrogenation of the exo olefinic bond has also caused an increase in the C-Cl bond stretch wavenumber by almost 10cm^-1.This could be due to overlap of the C-Cl σ* orbital with the exo olefin π-bond. Donation into the antibonding orbitals of the C-Cl bond would cause a slight decrease in the bond order resulting in it being weakened. Hence with the loss of this electron density from the double bond in the hydrogenated product, the C-Cl is no longer weakened and the stretch appears at a higher wavenumber.

Overall the MOPAC/PM6 semi-empirical MO modelling proved very capable in predicting the structures of the two compounds as well as accurately visually the MOs responsible for the regioselectivity of its reaction with an electrophile.

Monosaccharide chemistry: glycosidation

In glycosidation reactions, a leaving group is substituted with by a nucleophile via an oxonium ion (such as A & B in fig. 8). The orientation of the ^-OAc acetate group on the adjacent carbon to the substitution can cause the two sugars precursors to form different anomers almost exclusively. This comes as a result of the neighbouring group effect. For the α-anomer, its formation occurs via the topside attack of the acetyl oxygen on the oxonium cation which opens up the bottom face for attack by the nucleophile. Conversely, for the β-anomer, the oxonium is attacked from the bottom, allowing nucleophilic attack from above.

Figure 8 - Scheme showing the formation of the α and β-anomers which is affected by the placement of the acetyl group

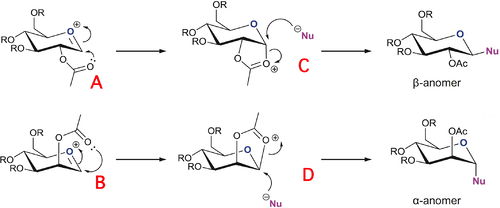
In this question, the oxonium intermediates will be modeled using a methyl for the R groups. This was chosen as it will not interfere with the calculations on the reaction centre due it being a small, simple group with no lone pairs. Additionally, using Me groups removes any possibility of hydrogen bonding simplifying the calculations significantly.

MM2 would not be appropriate as a modeling technique for this problem as it does not consider the orbital interactions of the acetate group and oxonium cation which are responsible for the regioselectivity of the end product. As discussed before, it functions using a basic ball and spring model based on classical mechanics and hence PM6 would be a much more sensible option as it considers the molecular orbitals particularly of the double bond where the acetate oxygen attacks.

MM2 can be put to good use by determining an initial geometry for each cation before using PM6 to take into account the orbital interactions.

Table 6 - Glycosidation calculations(all energies in kcal/mol)

Molecule	Stretch	Bend	Stretch-Bend	Torsion	Non-1,4 VDW	1,4 VDW	Charge/Dipole	Dipole/Dipole	Total Energy (MM2)	Heat of Formation (PM6)
	2.824	11.874	1.075	3.152	1.463	18.968	-25.581	5.910	19.685	-91.647
	2.505	10.720	0.963	4.227	-1.660	19.853	-10.413	4.228	30.421	-77.420
	2.501	13.003	0.959	1.419	-0.481	19.221	-20.490	6.664	22.797	-90.954
	2.487	9.460	0.906	3.149	-2.630	19.163	-1.019	3.963	35.480	-77.510
	2.014	13.701	0.694	8.348	-2.489	17.868	-8.199	-2.040	29.897	-91.651
	2.762	18.404	0.855	9.668	-2.514	19.469	1.445	-1.458	48.632	-66.841
	2.057	14.440	0.717	7.705	-3.389	17.626	-6.783	-0.910	31.461	-88.727
	2.650	19.516	0.791	8.964	-2.871	19.000	-1.510	-1.673	44.865	-67.005

It is clear to see that A & B are both much lower and hence more stable than A* & B* respectively when calculated using both MM2 & PM6 techniques. Again, these cannot be compared directly especially as one is based on classical mechanics and the other on MO theory, but they concur with eachother in terms of the relative stability of A vs. A* and B vs. B*. When trying to calculate the energies for the starred compounds, it was found that they tried to revert to the conformation of the non-starred one. This is clearly in concordance with what was found in the data as they are shown to be more unstable. The charge/dipole interactions arising from the very electronegative oxygens on the acetyl groups are clearly the largest factor in the difference in the energies of the two. This arises though the

Structure based Mini project using DFT-based Molecular orbital methods

Assigning regioisomers in "Click Chemistry"

As described by Sharpless and Kolb, the original idea behind "click chemistry" was to follow in Nature's footsteps by generating substances by linking together small units with heteroatoms (i.e. C-X-C). The goal was to develop "an expanding set of powerful, selective, and modular blocks" with which it would be possible to work on small- and large- scale processes. They outlined a set of criteria which they thought must be met for the reaction to be useful in this context. It must:

Figure 9 - Huisgen 1,3-dipolar cycloaddition

• be modular
• be wide in scope
• produce high yields
• generate easy to remove and inoffensive byproducts
• be stereospecfic (but not necessarily enantiospecific)

Additionally, they outlined that the features of the reaction process should include:

• simple reaction conditions without water or oxygen sensitivity
• utilisation of only readily available starting materials and reagents
• minimal use of solvent (none if possible or use of benign ones such as water)
• easy to isolate products

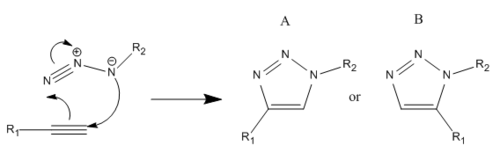
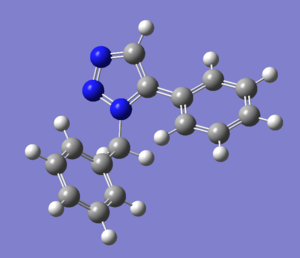
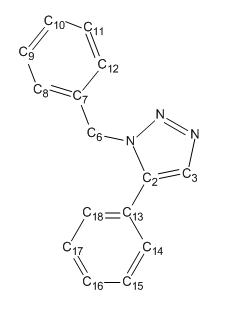
The premier example of a click reaction is the Huisgen 1,3-dipolar cycloaddition of alkynes and azides to yield 1,2,3-triazoles as shown in fig. 9. The facile syntheses of the alkyne and azide functionalities, as well as their kinetic stability and resistance to many functional groups and reaction conditions made this pairing of reactants particularly appealing. With substituted alkynes and azides, there are two possible regioisomeric products, A & B. However in 2002, when the discovery by two independent groups^, that a Cu(I)-catalyst could be used to speed up the reaction thrust this reaction into the spotlight of click chemistry. No protecting groups are needed, and under Cu(I) catalysis, almost completely favours the 1,4-disubstituted 1,2,3-triazole (A). Usually it is not necessary to purify the product and hence this reaction has become synonymous with CC, referred to frequently as "The Click Reaction". On the other hand, it was also found that under Ru (II) catalysis, it was found to favour the 1,5-isomer (B). The aim therefore of this mini-project was to utilise molecular modelling techniques in order to determine whether the two isomers can be distinguished using spectroscopic methods. The example to be investigated had R₁ = Phenyl group and R₂ = Benzyl group. This has been shown to produce two differing isomers, Y & Z (see fig.10); the percentage of each isomer produced dependant on the catalyst used.

Figure 10 - Products Y & Z

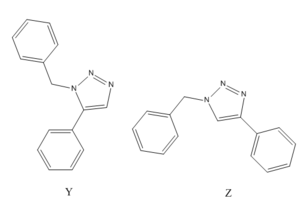
The two isomers were modelled in ChemBio3D and their geometries refined using simple MM2 calculations. For comparison, the geometries produced by using the AM1/mopac method are also displayed.

Table 7 - MM2/AM1 Calculation Results for Y & Z (all energies in kcal/mol)

Isomer	Stretch	Bend	Stretch-Bend	Torsion	Non-1,4 VDV	1,4 VDW	Dipole/Dipole	Total Energy	Heat of Formation (AM1)
	1.106	18.300	0.1075	-15.727	0.726	14.373	-1.663	17.223	143.448
	0.773	13.125	-0.030	-14.879	-1.650	14.710	-1.400	10.649	142.129

MM2 optimisation of Y gave a structure in which the 5-subsituted phenyl ring is planar, and in the same plane as the triazole. The -CH₂ in the group is also in the same plane but with its phenyl ring tilted at an angle of 112.9°. Repulsion between the delocalised electron clouds of the two phenyl rings may have caused this deviation from the ideal sp³angle of 109°. The more advanced AM1 optimisation produced a structure noticably different from the first. Both phenyl rings are now not in the same plane as the triazole ring, but are almost co-planar with eachother. The bond angle between the triazole and benzyl system is now 115° suggesting that this arrangement aromatic rings causes slightly more repulsion. This would be expected simply from looking at the basic structure as the almost parallel allignment allows for more steric interaction.

The MM2 optimised structure of Z resulted in a structure which was more stable than Y. This is demonstrated by the fact that the bond angle between the triazole ring and benzyl system is now 109.6°, much closer to the preferred sp³ hybridisation angle. This is reflected in the much lower bend energy for Z and negative stretch-bend which all indicate a less strained system. AM1 optimisation of this molecule again produced a slightly more stable structure than for Y as shown by the lower heat of formation and the reduced bond angle strain (114.3° vs 115°).

Overall the 1,4- disubsituted 1,2,3 triazole was found to be more stable than the 1,5- product as expected.

Following this, the two isomers were then optimised using DFT methods (method: mpw1pw91, basis set: 6-31G(d,p)).

Table 8 - DFT Optimised Geometries for Y & Z

Isomer	Image	URI
		DOI:10042/to-10362
		DOI:10042/to-10361

The DFT optimisisation of Y produced a structure resembling that of the AM1 optimised one with an angle of 114.4° between the triazole and benzyl group. This angle is between that of the MM2 and AM1, but suggests that the latter is the more accurate of the two as it was 0.6° out compared to 1.5°.

DFT optimisation of Z gave a structure resembling both the MM2 and AM1 calculated ones with a triazole-benzyl angle of 113.1°, a difference of 3.5° from MM2 and 1.5° from the AM1 calculated one. Again, this suggests that AM1 produces more accurate results than MM2 as both times, the difference in bond angle has been almost three times larger for MM2 compared to AM1.

Table 9 - NMR spectra for Y & Z calculated using mpw1pw91/6-31(d,p), Gaussview reference TMS mPW1PW91/6-31G(d,p) CDCl3 GIAO

Isomer	Full Spectrum	Carbon	Hydrogen	URI
Y				DOI:10042/to-10358
Z				DOI:10042/to-1036

Data

Assignment

Table 10 - 13C NMR Data for Y (CDCl3) Gaussian calculated Shift (ppm) Lit. shift (ppm) Integration Carbon assignment Discrepency 52.24 51.85 1 6 0.39 123.40 126.93 1 8 -3.53 123.66 127.22 1 12 -3.56 124.48, 124.69 128.22 2 10, 13 -3.63 125.07, 125.19 129.08 2 17, 9 -3.79 125.48, 125.61 133.26 3 11, 18, 15 -3.54 125.88 129.64 1 16 -3.76 126.22 133.26 1 14 -7.04 128.61 133.34 1 3 -4.73 134.11 135.66 1 7 -1.55 136.67 138.26 1 2 -1.29

Figure 11 - Click Y 13C assignment

The ¹³C NMR spectrum for Y calculated using the GIAO approach was fairly accurate giving an average discrepency of -3.28ppm (% difference 2.40-6.27%). C₆ is attached directly to a very electronegative nitrogen atom and so it would be expected to be deshielded quite heavily. This can be seen easily, as it appears the most upfield at 52.24ppm. The biggest error occurs with C₁₄ which deviates by 7.04ppm from the literature value. However, except for this anomalously large value, it should be expected that a computational approach may not agree with literature fully as an error such as incorrectly minimised geometry could be responsible for such a deviation. If the lowest energy conformer was not found, it would affect the intramolecular interactions and so distort the spectrum slightly.

Data

Assignment

Table 11 - 13C NMR Data for Z (CDCl3) Gaussian calculated Shift (ppm) Lit. shift - no data provided, read off spectrum (ppm) Integration Carbon assignment Discrepency 54.78 54.20 1 12 0.58 116.88 119.80 1 2 -2.92 121.22 126.00 1 11 -4.78 121.78 128.10 1 7 -6.32 124.10 128.20 2 9, 18 -4.10 124.80 129.00 3 16, 15, 10 -4.21 125.29 129.30 2 8, 17 -4.02 127.62 130.80 1 6 -3.18 133.11 134.80 1 13 -1.69 144.75 148.00 1 1 -3.25

Figure 12 - Click Z 13C assignment

The average discrepency for the NMR of Z was -3.39ppm, though this did not include as large a value as for Y (-7.04ppm). This gives a percentage difference range of 2.34%-6.19%, which is almost identical to that found for Y. This shows that in this case, the ¹³C has a consistent error of approximately 4.30% which is fairly low.

Table 12 - IR spectra for Y & Z calculated using b3lyp/6-31G(d,p)

IR peaks

Spectra

Peak type Wavenumber/ cm-1 (Y) Wavenumber/ cm-1 (Z) C-H stretch (triazole) 3275.87 3295.37 C-H stretches(Phenyl ring) 3214.50, 3209.10, 3201.22 3221.26, 3204.87, 3193.22 C-H stretches (Benzyl ring) 3210.65, 3203.74, 3193.73 3209.54, 3199.56, 3190.87 Benzyl CH2 stretch 3130.69, 3076.36 3122.76, 3071.21 C=C stretch (Phenyl ring) 1662.49 1665.87 C=C stretch (Benzyl ring) 1662.03 1663.48 N-N stretch 1282.51 1309.30 C-H bend(Triazole) 840.37 771.49 C-H bend(Phenyl) 779.66 771.49 C-H bend (Benzyl) 743.48 744.02

Isomer Spectrum URI Y DOI:10042/to-10363 Z DOI:10042/to-10364

The two IR spectra agreed pretty closely in terms of the stretches found; however there were enough notable differences which allow differentiation between the two isomers. In particular, the change in N-N stretch from 1282.51-1309.30cm^-1 would be the stretch with which it is most facile to assign the product's regioselectivity.

The free energies of the Click isomers were also calculated using the DFT method. Y gave an energy of -743.668 kJmol^-1 compared to -743.671 kJmol^-1 for Z. This is therefore fairly unhelpful in determining between the two isomers.

The DFT calculated NMR were fairly accurate in comparion with literature values, and the IR spectrum allowed for differentiation between the two products though the different in the N-N stretch wavenumber. With more time, different, more complex R-groups could had been tested to see how the DFT modelling handled the predicted of spectra for them. Although the NMR seemed to have a fairly consistent percentage error, a data set of two is of course statistically insignificant and testing it up against more complex structures would have given a more complete test of its abilities.

Conclusion

Three different methods of molecular modelling were tested here, from the basic, classical mechanics based force field up to the ab initio quantum mechanical approach. It was successfully shown that as more factors, such as orbital interactions, were taken into account by the more advanced methods, the modelling became more accurate and more relevant to the requirements of a computational chemist. Being able to predict an NMR spectrum to with 2-7% of its expected range, as was done here, or how frontier molecular orbitals will be distributed, are valuble tools for chemists who can now spend less time performing trial and error time experiments, and instead test out their theories without waste of lab time and resources.