Rep:Mod:Pphys89
Module 3: Computational Techniques in Physical Chemistry
Introduction
As well as being useful in studying the observed states, such as reactants and products in a given reaction the true usefulness of computational techniques is the ability to generate and study the transition states of the reaction. The following report will be a demonstration into the ways that transition states of simple reactions, the cope rearrangement and Diels-Alder cycloaddition, can be generated and studied.
Cope Rearrangement of 1,5-hexadiene
The Cope rearrangement is one of the classical pericyclic reactions which in effect is a [3,3] sigmatropic rearrangement of a 1,5-diene, which in this case is the simplest possible 1,5-hexadiene. The net effect of the reaction is the 3 carbon shift of a sigma bond:
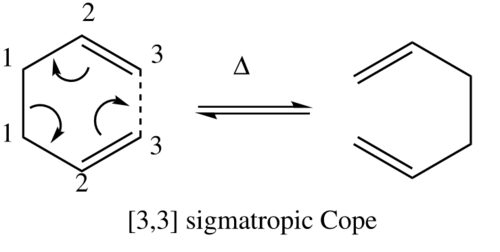
The reaction proceeds through an aromatic transition state where the two allyl type fragments are in an arrangement that resembles the chair or boat conformation of cyclohexane. The reaction can be predicted to proceed through the transition state with the lowest energy as it will have the lowest activation energy.
Optimisation of the reactants/products
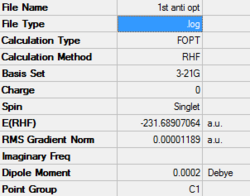
The hexadiene has the conformationally active C-C bonds giving a large number of conformations that can be studied, however, in the following only the middle (C2-C3) carbon bond will be considered. Both an anti conformer (fig 1) and a gauche conformer (fig 2) of the 1,5-hexadiene were constructed in Gaussview and then optimised using the Hartree-Fock method with the 6-31G Basis set.
The point group of both of the conformers was, upon further investigation, determined to be C2h and C2 for the anti- and gauche-conformers respectively. From this data and the relative energy of the conformer it was deduced that they are labelled anti3 and gauche1 conformations. These are two of many conformers that can be populated by 1,5-hexadiene. Of the other conformers it is interesting to note that despite the heightened steric interaction between the two alkene groups in the gauche conformation one of the gauche conformations is the lowest in energy. This suggests there are electronic factors dominating the steric interaction and in fact it can be shown that there is a combination of overlap between the pi systems and vinyl hydrogens as well as stabilising pi-pi interaction in the gauche conformer that makes it the lowest in energy. A low level calculation (3-21G basis set) was used to produce the MOs of the gauche conformer:

Gauche_overlap.png It can be seen that there is extensive conjugation between the two pi bonds showing that there is a extensive overlap between the two ends of the moelcule which can stabilise the conformation. No interaction was found between the vinyl Hydrogens and pi system therefore it can be concluded that the pi-pi stabilisation is the main reason behind the gauche conformer being the most stable.
Following the low level optimisations the effect of changing the basis set to a higher level basis set and the anti2 conformer with Ci symmetry was used as the study molecule. The point group in the HF optimised molecule was constrained to Ci symmetry for "all changes", which means that any changes that happen to the molecule will occur with retention of the original point group. The molecule was then optimised with both the HF/3-21G and DFT-B3LYP/3-21G+ methods.
| Method | Energy/a.u. | C=C bond length/A | C-C bond length/A | C1-C4 dihedral angle | C2-C6 dihedral angle | H-C1-C2 angle |
|---|---|---|---|---|---|---|
| HF Optimised | -231.69253529 | 1.34150 | 1.55504 | 114.68930 | -114.68930 | 121.82602 |
| DFT Optimised | -234.57110312 | 1.34150 | 1.55504 | 119.42297 | -119.42297 | 121.87366 |
The reference energy for the HF optimisation given was -231.69254 showing that the calculations carried out show good agreement with the previous calculations taken.
The DFT method gives a lower energy by ca. 3au showing significany electronic stabilising interactions that are not taken into account in the lower level theory. The origin of the differences involves the amount of approximations used in the formulation of the molecular orbitals, which translates through to the structure of the molecular orbitals and the ability to model intramolecular orbital interactions (such as the one in the gauche conformation) is adversely affected. The stabilising interaction that occurs is due to an interaction between the pi orbital and vinyl proton and hence the strength of the interaction is dependent on orbital size from which the dependence on the basis set and methods arises. The difference in strength of the orbital interactions means that there will be different energy minima that can be determined for the structures, it can be seen that the dihedral angle representing the orientation of the -C(H)=CH2 relative to the alkane C3-C4 backbone, increases for the DFT method
To confirm the true minima had been obtained a frequency analysis was ran on the structure and as there were no negative frequencies it was concluded that the structure found was the structural minima. The lowest real ie. observable frequencies was 78cm-1 and the spectra generated was:

In addition to being able to generate the vibrations and corresponding spectra of a complex the vibrational analysis gives an insight into the energetics of a complex (which are automatically calculated at 0K) and some of the important results are summarised below:
| Property | Quantity/au |
|---|---|
| the sum of electronic and zero-point energies | -234.428071 |
| the sum of electronic and thermal energies | -234.420755 |
| the sum of electronic and thermal enthalpies | -234.419811 |
| the sum of electronic and thermal free energies | -234.459734 |
Ci frequency file:DOI:10042/to-7268
Investigating the Methods Used in Transition State optimisation
Following the optimisation of the reactants/products Gaussian was used to compute the two possible transition states of the reactions, which are the Boat or Chair type transition states:
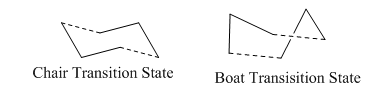
The two transition states can be easily differentiated by the symmetry point group of Transition state which is C2h for the Chair transition state and C2v for the boat transition state. The transition state can be modelled using two allyl fragments 2.2A apart, orientated to form the required symmetry for the transition states. Therefore, the starting point was a optimisation of an allyl fragment, which was done using the HF/3-21Gmethod (minimum energy=-115.823au).
Frequency Analysis
The Chair transition state will be the first of the structures to be probed, a "guessed" structure was constructed with 2 of the optimised allyl fragments orientated so that the terminal Carbons were 2.2A apart and the overall symmetry of the structure was C2h. Using the HF/3-21G method and basis an optimisation and frequency analysis was ran on the structure to give the perceived intermediate:
| Structure | Analysis Summary | |||
|---|---|---|---|---|
|
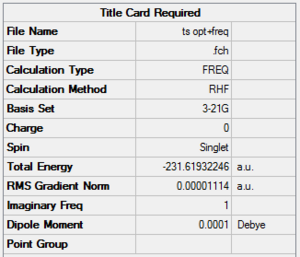 |
The key evidence demonstrating that the structure was a Transition State was the solitary negative frequency of magnitude -818cm-1, which is in very good agreement with the reference frequency given. The frequency inolves the simulataneous bending of two terminal carbons towards each other and the other two terminal carbons bending away from each other demonstrating the Cope re-arrangement. A second method for the optimisation of the chair structure involves the Frozen co-ordinate method and this gave a structure and vibration indicative of reaction that was resembled the one found by the Berny process. The structures were in fact pretty much identical which is demonstrated by the same frequency of 818cm-1 and structural energy of -213.619au for both methods. This demonstrates that for the given molecule and other related molecules the frozen co-ordinate and Berny methods are exactly the same apart from the 2 steps require in the frozen co-ordinate method compared to the one in the Berny method. The disadvantages of using the frozen co-ordinate method apart from the 2 steps require is that it requires a relatively good understanding of the reaction mechanism as it must be known which distances can be fixed in length whereas by comparison the Berny method only requires knowledge of how the reactants approach each other and the calculation determines the rest msking it a better method for studying mechanism that are not fully understood
Extrapolation from the reactant and product's structures Using the QST2 Method
Another of the ways that can be used to determine a transition state is by considering the reactants and the products of the reaction and extrapolating out from these to give an intermediate geometry, which is predicted to be a transition state (and can be shown by a single negative frequency in the frequency analysis). This method was used to determine the boat transition structure. Firstly the optimised hexadiene was taken as the reactant and product, the QST2 analysis was ran using the HF method and 3-21G basis set. This calculation failed, which can be attributed to the sensitivity of the QST2 analysis to the starting geometries and hence is can be concluded that the actual products aren't close enough to the transition state for the QST2 analysis to work. This is due to the ability of the 1,5-hexadiene to rotate about the central C(3)-C(4) bond to give structures with very different energy minima. As the anti2 structure is a very low energy minima the QST2 could not successfully locate a path along the potential energy surface to the transition state's location. To remedy this, one of the vinyl groups was rotated about so that the C2-C3-C4-C5 dihedral angle was 0o and the angle from the carbon backbone to the vinyl groups was 100o. The QST2 analysis was again run again and a boat transition state was successfully obtained: The structure gave a single negative frequency at -840cm-1 which corresponds to the movement of the groups required for the Cope rearrangement. The Results of the analysis are summarised in the following table:
| Structure | Summary | Bond-Forming Vibration | |||
|---|---|---|---|---|---|
|
 |
 |
The image of the vibration has the movement of the atoms demonstrated using displacement vectors (blue arrows), which shows that two terminal carbons move towards each other in a bond forming movement whilst there is the simultaneous movement of the other two terminal carbons away from each other signifying a bond breaking movement. The distances between the allyl fragments at the terminal carbons are 2.4105 and 2.4104A showing. For a totally concerted mechanism with an aromatic intermediate we would expect both of these of distances to be the same. Therefore, from this it could be concluded that the QST2 method is not a sufficiently high level of theory to properly compute the transition state and further work in this area would ideally use the QST3 method or use a further optimisation of the transition state using a high level theory eg. DFT-B3LYP/6-31G+ method and investigate what happens to the structure.
The IRC Analysis
From the structures of the Transition states determined above further analysis can be ran on them. The Intrinsic Reaction Co-ordiante allows us to track the movement of the structure across the transition structure across the transition state to a local energy minimum, hence locating the structure of the product (or reactant) that is closest to the transition state making it in effect a computational demonstration of the Hammond Postulate. Whilst the analysis can be ran in two directions for a reversible reaction, given that the Cope re-arrangement is symmetrical the IRC only needed to be calculated in the forward direction:
| Transition state | Energy Plot | RMS Gradient Plot | Final Structure | Summary | |||
|---|---|---|---|---|---|---|---|
| Chair | 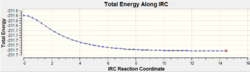 |
 |
|
 | |||
| Boat | 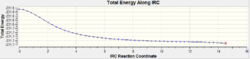 |
 |
|
 |
The key feature of the energy and RMS plots revolves around the plateaus at the end of the plots as these are indicative that the calculations are not able to change the structure to give a lower energy conformation and so coupled with the fact the calculations terminated before the maximum 50 steps it could be concluded that the minimum energy structures had been successfully determined.
--- Boat IRC file: DOI:10042/to-7270 Chair IRC file: DOI:10042/to-7271
Frequency Analysis and Activation energies
Whilst the two possible transition states for the reaction have been successfully computed in the earlier sections the two can't be compared due to the differing methods used and therefore for a final analysis both structures were optimised with a frequency analysis using the same method (bothHF/3-21G and DFT-B3LYP/6-31G+) and then compared:
| HF:Chair DOI:10042/to-7195 | DFT:Chair doiDOI:10042/to-7205 | HF:Boat | DFT:Boat DOI:10042/to-7204 | Anti2 Starting Conformer (HF) | Anti2 Starting Conformer (DFT) | |
|---|---|---|---|---|---|---|
| Total Energy/au | -231.619322 | -234.556983 | -231.602802 | -234.54309304 | -231.692535 | -234.611710 |
| Sum of Electronic and zero Point energies/au | -231.466700 | -234.414919 | -231.450929 | -234.402339 | -231.539539 | -234.469203 |
| Sum of Electronic and thermal energies/au | -231.461341 | -234.408998 | -231.445300 | -234.396005 | -231.532566 | 234.461856 |
| Activation Energy (0K) | 45.94 | 34.09 | 55.60 | 41.96 | N/A | N/A |
The reference calculated (DFT) and experimental values for the activation energies were 33.17kcal/mol and 33.5±0.5kcal/mol respectively. Firstly it can be seen that the values determined in this experiment are in very good agreement with the reference value given. Secondly there is a strikingly good agreement between the DFT calculated value and the experimental value showing that the ability of high level calculations to reproduce experimental data without the need for running lab based experiments.
One of the striking differences is the change in energy and accuracy upon changing from teh HF/3-21G to DFT-B3LYP/6-31G+ methods which reduces the energy by about 4au. This is most likely due to the ability of the B3LYP to model molecular orbitals better and hence give a better demonstration of the varying attractive forces that are found in the molecule.
Finally it can be seen that the activation energy is much lower for the Chair transition state compared to the Boat transition state and so it can be concluded that the Cope rearrangement proceeds through the Chair like transition state found earlier.
Study into the Diels-Alder Cycloaddition
Orbital Control in the Diels-Alder reaction
Taking the simplest example of ethene and cis-1,2-butadiene the orbital interactions leading to the reaction and formation of the product molecule can be demonstrated. As usual the key orbitals are the HOMO and LUMO orbtials of the reactants, for ethene this is just the pi bonding and anti-bonding orbitals. However the orbitals are more complex for cis-butadiene and so these were produced using the semi-empirical methods using the AM1 method.
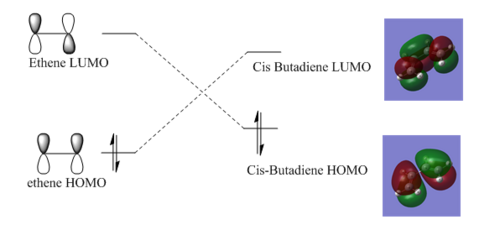
The dotted lines demonstrate the symmetry match up (ie superposing the two orbitals leads to bonding interactions but no nodal planes formed) between the HOMO of ethene and LUMO of butadiene-symmetric relative to the plane- and also the possibility of butadiene's HOMO and the LUMO of ethene -anti-symmetric relative to the plane-. These interactions only occur when the reactants approach from above or below each other (but not side on). The actual bonding interaction depends on the relative energies of the bonding and anti-bonding orbitals with the orbitals closer in energy giving a higher interaction, in accordance with the Klopman-Salen equation and can't be predicted without the orbitals of both molecules being simulated using the same methods. For reference the relative energies of the Butadiene's HOMO and LUMO were -0.34383 and 0.01709 au respectively. In addition the energies of ethene's HOMO and LUMO are -0.38774 and 0.05285 respectively.
The Diels Alder Transition State
From the orbital control demonstrated above it can be seen that the ethene fragment must approach the cis-butadiene fragment from above the plane of the molecule and so it can be approximated that the transition state involves the ethene fragment being in close proximity to the diene forming an envelope type structure. The Distance between the terminal carbons was arbitrarily chosen to be 2.2A. Then the structure was optimised to the transition state (Berny) with a frequency analysis using the AM1 semi-empirical method. The Transition state was successfully located, which is demonstrated by the single negative frequency at -956cm-1 corresponding to the terminal carbons bending towards each other as required for the formation of the two new C-C bond formed in a Diels Alder reaction:
| Structure | Bond Forming Vibration | Lowest Real Frequency | |||
|---|---|---|---|---|---|
|
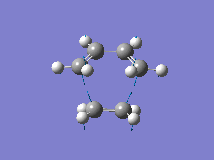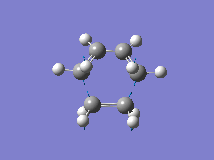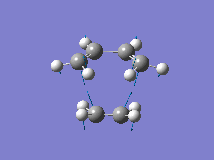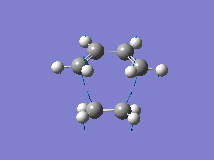 |
|
The distance between the two fragments ie. the length of the new C-C bonds was 2.12A, the length of the forming double bond was 1.40A and the original double bonds in the diene had increased in length to 1.39A. Furthermore, the dihedral angle across the trans Hydrogens in the ethylene fragment was -154o and the H-C-H bond angle had decreased from 120o to 115o showing that the hybridisation of the ethylene Carbons is changing from sp2 towards sp3. This is supported by the negative (bond forming) frequency where the ethene Carbons bend up towards the diene with the Hydrogens bending downwards visually demonstrating their change in hybridisation. The bondforming vibrations is a synchronous movement By contrast the lowest real frequency (147cm-1) involves a twisting of the two fragments in opposite directions (the diene rotates clockwise and the ethene rotates anti-clockwise)
In addition to the frequency analysis the AM1 method also produces the molecular orbitals for the complex and these were produced to compare with what had been predicted earlier.
| HOMO | LUMO |
|---|---|
 |
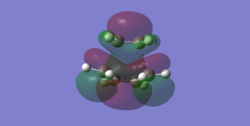 |
Taking the plane of symmetry as bisecting the ethene (and newly forming C=C bond) it can be seen that the HOMO is anti-symmetric with respect to the plane and the LUMO is totally symmetric with comparison to the plane. It was also interesting to see that in the LUMO there is electron density delocalised between the double bond of ethene and C3-C4 of the diene. This suggests that we are seeing a combination of the ethene HOMO and diene LUMO, from which we can conclude for the given AM1 method that this gave a MO higher in energy that for the combination of the diene HOMO and ethene LUMO. However, given the ordering of these orbitals is a direct consequence of how good the basis set used is meaning that for computing molecular orbitals the higher basis set is always better.
Regioselectivity in the reaction between Maleic Anhydride and cyclohexa-1,3-diene
After the discovery of the Diels-Alder reaction it was increasingly noticed that there was a surprisingly high selectivity for the endo product even though it was predicted (and later proved) to be the product highest in energy. Computational techniques were later used to show that this was a result of a "secondary orbital interaction" where the orbitals not-involved in the Carbon-Carbon bond forming interact to stabilise the transitions state thus the product formation becomes a balance between steric and electronic factors. The following reaction between Maleic Anydride and Cyclohexa-1,3-diene will be used to investigate this effect.
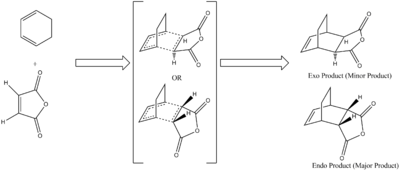
In order to set up the reaction both the Maleic anyhdride and cyclohexadiene were optimised using the HF/3-21G method followed by the DFT-B3LYP/6-31G+. Following this the two molecules were orientated in such a way that they were likely to form the exo/endo product and from this set up the distance between the Carbons where the bond forming occurs was reduced to 2.2A before the structures were optimised to the Berny Transition State (with frequency analysis). This method worked for to give the exo transition state, however the endo structure also optimised to the exo transtion state and so to remedy this the frozen co-ordinate method previously used was employed and this successfully resulted in the transition state being determined.
| heading | Exo | Endo | ||||||
|---|---|---|---|---|---|---|---|---|
| Original Structure |  |
 | ||||||
| Transition State |
|
| ||||||
| Energy/au | -612.19504 | -612.519864 | ||||||
| Bond forming (C3-C12) and C2-C11/A | 2.19 | 2.26 | ||||||
| C10-C13 (double bond forming) length/A | 1.42 | 1.41 | ||||||
| C12-C13/A | 1.39 | 1.41 | ||||||
| Distance between Maleic Anhydride group and nearest neighbour | 2.71 | 3.41 | ||||||
| Negative Frequency | -445cm-1  |
-445cm-1  |
It can easily be seen that in the above table the Endo transition state is lower in energy than the exo transition state and hence has a lower activation energy and forms quicker. This supports the experimental visualisation that the endo is the major product in a kinetically favoured reaction. The distance between the C(O)-C-C(O) fragment and the diene is much larger in the endo transition state from which it can be concluded that there is likely to be a lower steric repulsion between the oxygen lone pairs and the diene ring, which contributes to the fact that the endo state is lower in energy. To investigate whether the proposed secondary orbital effect could be seen to have any effect the MOs of the two structures were visualised. As the basis set has a direct effect on the ordering of the molecular orbitals it can't be said for certain which MO is the actual HOMO/LUMO and so the HOMO-1 to the LUMO+3 are going to be considered for the analysis. Given the sensitive nature of the interactions between different orbitals relative to the basis set used, the most powerful 6-31G+ basis set was used along with the DFT-B3LYP method to produce the following orbitals:
| Type | Exo Structure | Endo Structure |
|---|---|---|
| LUMO+1 | 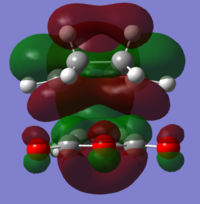 |
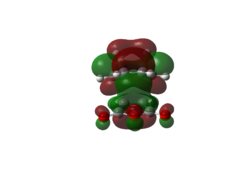 |
| LUMO | 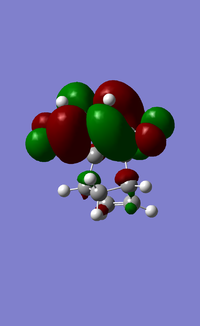 |
 |
| HOMO |  |
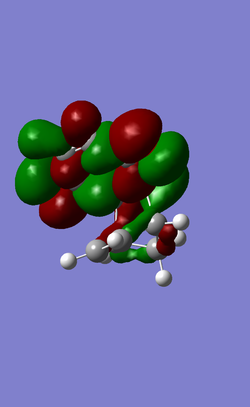 |
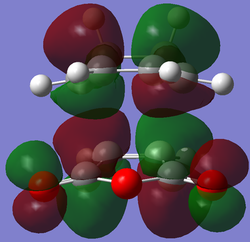
| HOMO -1 | 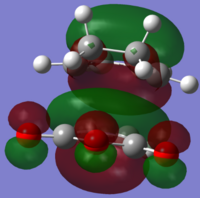 |
 |
For a simple comparison below is the "Secondary Orbital Interaction" demonstrated with the dimerisation of cyclopentadiene:
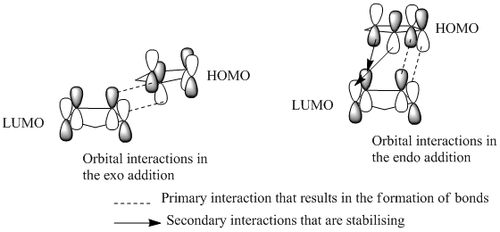
For the seconadry orbital overlap which is predicted to occur in the endo molecule we would expect to see part of the molecular orbital extending from the anhydride fragment to the diene fragment which would be indicative of a strong interaction between the orbitals not involved in the C-C bond forming. From the images of the orbitals it can be seen that the HOMO shows no possibility of a secondary interaction. The HOMO-1 shows the possibility for an interaction between the carbonyl oxygen and pi system on the forming C-C bond similarly for the LUMO and LUMO+1 there are symmetry allowed orbital interactions (ie. parts of the MOs with the same phases). However as there is no linkage between the two it is difficult to evaluate whether they are interacting or not.
If we then look at the Frontier orbital diagram which is often used to rationalise the “secondary orbital effects” immediately there is the problem that the FO analysis only considers the symmetry of the orbitals and not their energy when considering whether there is the possibility for an interaction. Therefore whilst it provides a convenient basis with which the stabilisation can be rationalised, it gives absolutely non information into whether they can interact through energetic means, which is the main problem with using this method.
In conclusion, it is difficult in this case to argue that there is a significant orbital overlap effect that influences the selectivity of the reaction as opposed to the increased strain in the exo form, which makes it higher in energy. It is also worth noting that in the calculations, Solvent effects have been neglected, the choice of solvent could have a large influence on the way that the two molecules approach each other depending on the co-ordination shell around each molecule. This is especially relevant for the polar C(O)-C-C(O) group where the interactions between polar or non polar could have an influence on the reaction. Furthermore, solvents can effect the molecular orbitals through their interactions with the different functional groups eg. For the carbonyl group H-bonding solvents will interact with the Oxygens removing electron density away from the carbon and changing the energy and form of the molecular orbitals, which could possible affect the way that they interact with the other MOs and add to or detract from the “secondary orbital interactions” --- Endo file DOI:10042/to-7273 Exo file DOI:10042/to-7276