Rep:Mod:Pm1912
EX3 Section
Job files and Summary tables
Geometry Information
| BH3 | BBr3 | GaBr3 | |
|---|---|---|---|
| r(E-X) Å | 1.19 | 2.02 | 2.39 |
| θ(X-E-X) degrees(º) | 120.0 | 120.0 | 120.0 |
Optimisation Calculations
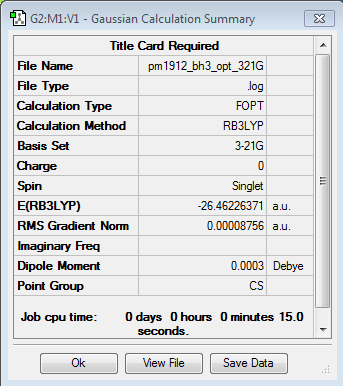
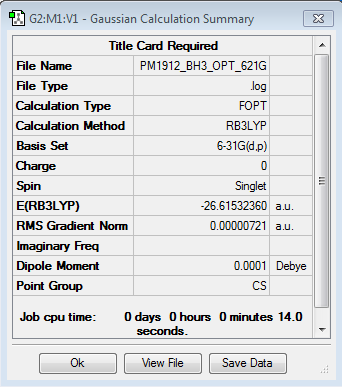
Borane
B3LYP/3-21G level
Optimisation log file here
| Summary Data | Convergence | Jmol | |||
|---|---|---|---|---|---|
 |
 |
|
B3LYP/6-21G level
Optimisation log file here
| Summary Data | Convergence | Jmol | |||
|---|---|---|---|---|---|
 |
 |
|
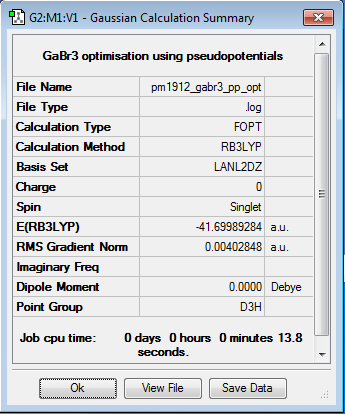
Gallium Bromide
B3LYP/LANL2DZ
Optimisation log file DOI:10042/87407
| Summary Data | Convergence | Jmol | |||
|---|---|---|---|---|---|
 |
 |
|
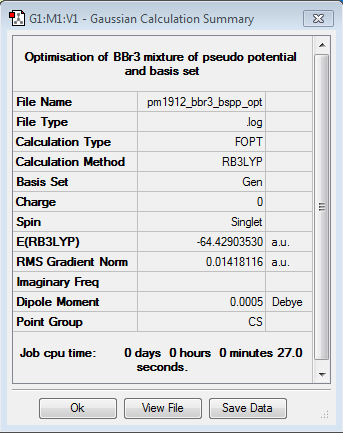
Boron Tribromide
B3LYP/6-31G(d,p)LANL2DZ
Optimisation log file DOI:10042/87532
| Summary Data | Convergence | Jmol | |||
|---|---|---|---|---|---|
 |
 |
|
Analysis
An increase in size of the ligand, in this case from hydrogen to bromine, increases the bond length. This is because of orbital enlargement, the increased size means more space is taken up between the atoms and they are pushed further apart. The equilibrium energy of the bond is at a greater bond length for heavier atoms. It makes sense then, that the molecule composed of the heaviest molecules (GaBr3) has the greatest bond length.
Bromine is a much heavier element than hydrogen being in group 7 rather than in group 1. Being a halogen and therefore an electron acceptor it can react with hydrogen which is an electron donor. Bromine is also in period 4 so has a far greater number of electron shells making it larger in size.
Changing the central atom from boron to gallium increases bond length slightly, though not on the same scale as the ligand difference. This is again due to orbital expansion as larger orbitals will use more pace and therefore make the bond longer. Gallium will use its 4p orbital while boron only has a 2s orbital, which is significantly smaller, decreasing the atomic radius.
Boron and gallium are in the same group and both have 3 electron in their outermost shell, each with one electron in the valence p orbital. However, boron is in the 2nd period while gallium is in the 4th period, making it much larger due to having more electron shells and therefore its valence orbitals are also larger.
Smaller atoms can get closer to each other and therefore have greater overlap, better overlap is also achieved when atoms involved in bonds are of similar size so their orbitals are also of similar size enabling better overlap and therefore bonding. This latter point is true for both BH3 and GaBr3 but for BBr3 the orbital overlap will not be as good and this corresponds to the larger bond length. The more electronegative an atom is the more it pull electrons towards it and the stronger the bond length ergo a shorter bond. Bromine is quite electronegative so this strengthens the bonds but not enough in either GaBr3 or BBr3 to make the bonds as strong as in BH3.
Some Background Information
A bond is an interaction between orbitals of two different atoms. The orbitals overlap and this causes a molecular orbital to form from the two atomic orbitals. The orbitals interact because of the donation and acceptance of electrons between them. The exchange is what causes the electrostatic attraction between the molecules and forms the bond. A bond is the most stable distance between two atoms at an energy minima.
An example of a strong bond would be the nitrogen – nitrogen triple bond which has a mean bond energy of 946 KJmol-1. This bond has so much energy because three pairs of orbitals are involved in the bond. Not just the σ molecular orbitals but two π molecular orbitals are also adding to the bond strength. A medium bond would be like the oxygen double bond O=O, which has a mean bond enthalpy of 497 KJmol-1 which is less than half than the previous example. On top of the σ orbital interaction there is also one π orbital interaction making the bond stronger. An example of a weak covalent bond would be the iodine – iodine (I-I) bond. This only has a mean bond enthalpy of 151 KJmol-1 because there is only one σ molecular orbital, and the molecule does not suffice the octet rule well. Even weaker than any of these intramolecular bonds are intermolecular bonds such as instantaneous dipole – induced dipole bonds, or hydrogen bonds. These are purely electrostatic interactions dependent on the charge or dipoles of molecules and are on the scale of 21 KJmol-1.[1]
Gaussview draws bond based on the distance between the two atoms and whether this distance is within the criteria for it to draw a bond. Therefore is there are no bonds shown the bond length is greater than some pre-defined value, but there is still a bond there.
Frequency Calculations
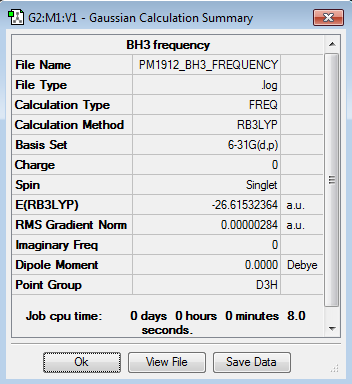
Borane
B3LYP/6-31G level
Frequency file here
| Summary Data | Low Modes |
|---|---|
 |

|
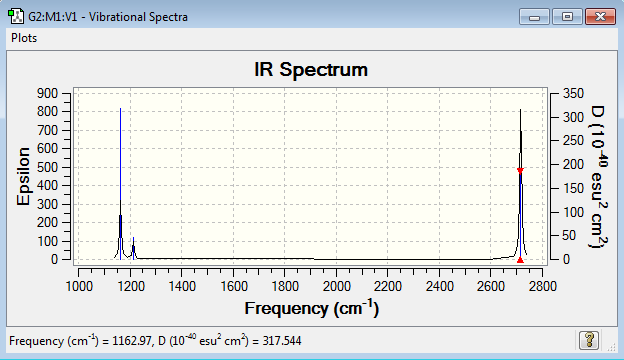
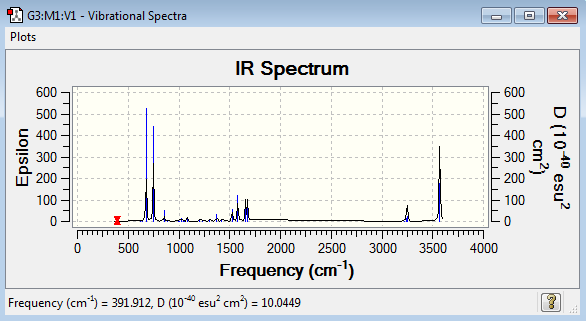
Vibrational spectrum for BH3
| Wavenumber (cm-1) | Intensity | IR Active? | Type |
|---|---|---|---|
| 1163 | 93 | yes | bend |
| 1213 | 14 | very slight | bend |
| 1213 | 14 | very slight | bend |
| 2583 | 0 | no | stretch |
| 2716 | 126 | yes | stretch |
| 2716 | 126 | yes | stretch |
Judging by the 3N-6 rule there should be 6 modes of vibration for BH3 and there are. But only three peaks are present on the IR spectrum. One of the vibrations (2583 cm-1) has an intensity of 0, this is because it is not IR active. The vibration is a totally symmetric stretch so there is no dipole movement in the molecule and therefore it is not detected by IR spectroscopy. There are also two pairs of vibrations (1213 and 2716 cm-1) that are degenerate. This means that they have the same energy and therefore the same wavenumber. So they both appear as the same peak on the same spectrum.
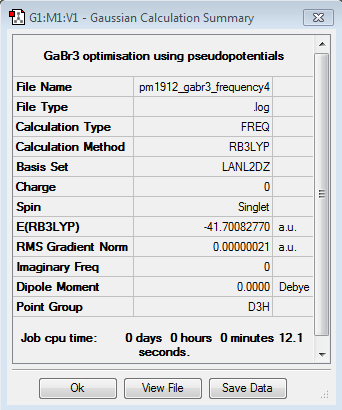
Gallium Bromide
B3LYP/LANL2DZ
Frequency file DOI:10042/90460
| Summary Data | Low Modes |
|---|---|
 |
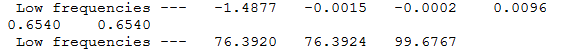
|
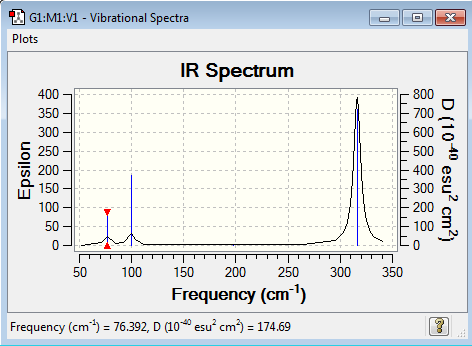
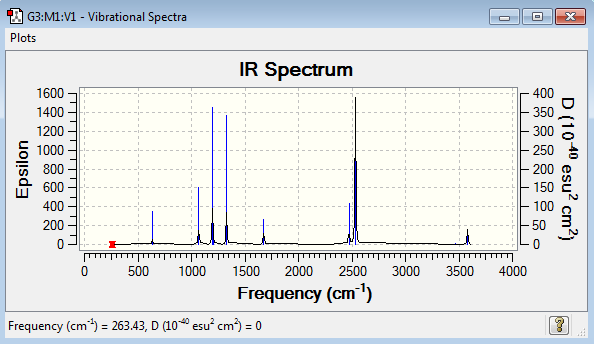
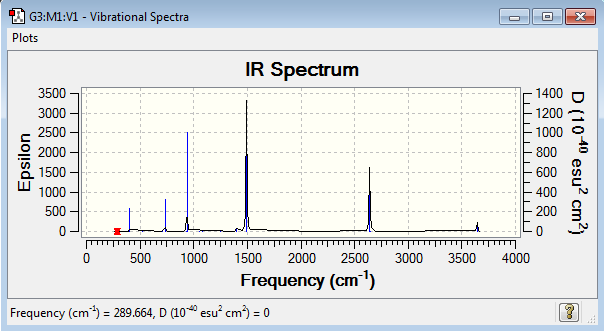
Vibrational spectrum for GaBr3
| Wavenumber (cm-1) | Intensity | IR Active? | Type |
|---|---|---|---|
| 76 | 3 | very slight | bend |
| 76 | 3 | very slight | bend |
| 100 | 9 | very slight | bend |
| 197 | 0 | no | stretch |
| 316 | 57 | yes | stretch |
| 316 | 57 | yes | stretch |
Analysis
The vibrational frequencies of BH3 are much larger than that of GaBr3 and its IR spectrum is focused around wavenumbers in the 1000 – 3000 cm-1 while that of GaBr3 is below 350 cm-1. This large difference indicates that the bonds in BH3 have a much higher energy than the GaBr3 bonds so are therefore stronger. This analysis is backed up by the previous optimisations where the bond lengths in BH3 are shown to be less than in GaBr3 as shorter bond lengths correspond to stronger bonds. Also heavier atoms vibrate less frequently than lighter atoms, this is why GaBr3 vibrates at such a lower frequency compared to BH3.
The A2’’ motion in BH3 is a peak at 1163 cm-1 while in GaBr3 it is a peak at 100 cm-1 and now has a higher wavenumber and therefore energy of the two E’ degenerate bend vibrations. From BH3 to GaBr3 the frequency has decreased from 1163 cm-1 to 100 cm-1, while the intensity has decreased from 93 to 9. This has not decreased as much as the degenerate E’ orbitals so the modes have been reordered. In BH3 the boron atom moves a lot less than the hydrogen atoms along the z axis in terms of displacement while in GaBr3 gallium moves mores along the z axis than the bromine atoms. GaBr3 has a larger displacement vector than BH3, this is because it is composed of much heavier atoms, so the bonds between the atoms are weaker and they are able to move more freely and further away from each other. Bromine is in group 7, so due to its busy valence shell its displacement vector is reduced and therefore gallium moves further in GaBr3.
Some Background on Frequency Calculations
When optimising the molecule the method and basis set used depends on the elements in the molecule and how heavy they are, as heavier molecules require longer calculations. This does not change for frequency calculations as the element in the molecule have not changed and still require that particular method and basis set. To make a meaningful comparison between two calculations the basis set and method have to be the same otherwise the comparison is meaningless.
A frequency analysis finds the energy minima by calculating the second derivative of the potential energy surface. It also allows the vibrational movements of molecules and IR/Raman modes to be studied. The products of a calculation show all the different modes of vibration, their energies and intensities. From this data degenerate modes can be found and IR active and IR inactive modes distinguished. An IR spectrum can be plotted with all the vibrational peaks. This can be used to compare with IR from experiments to see if a particular molecule is present.
The low frequencies represent the motions of the centre of mass of the molecule and are taken off from the modes of vibration by the 3N-6 equation.
Energy Calculations
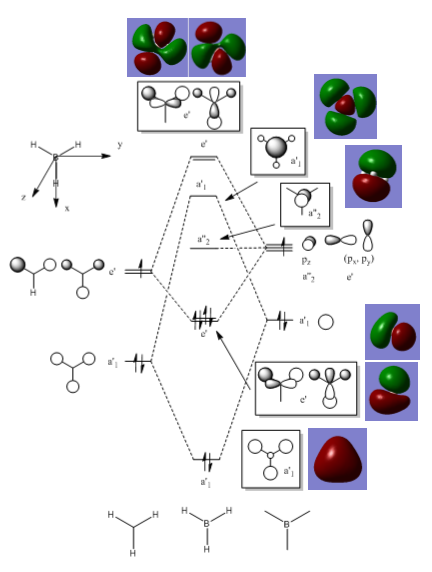
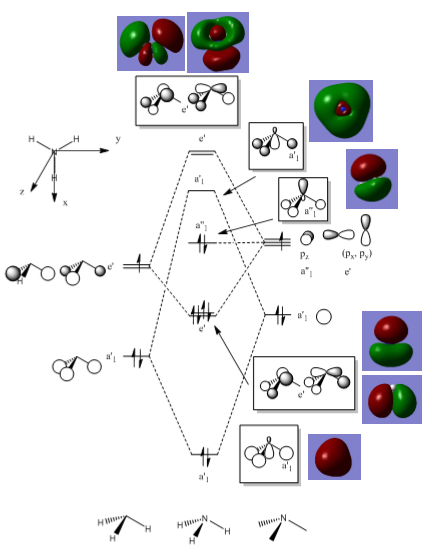
MO diagram for Borane
B3LYP/6-21G level
Population file DOI:10042/93155
Analysis
The qualitative model is a good approximation of the MO are it estimates correctly where the orbitals will be and what phase they are in. The main difference in the real MOs is that the orbitals are more diffuse so appear as one large orbital for each phase. Also in the real MOs the orbitals are not always of equal size as seen in the degenerate E’ orbitals where one phase appears larger than the other. This is not predicted in the qualitative model. For example the LCAO MO for the bonding A’1 symmetry shows contributions from each of the s orbitals from each of the atoms. Whereas in the real MO the different atomic contributions cannot be distinguished, the MO instead appears as one large orbital encompassing the molecule. This overlap of orbitals is seen in all the real MOs where bonding orbitals and anti-bonding orbitals merge respectively into one large orbital creating a very different picture form the LCAO MOs.
However, there is still a strong relation between the two as qualitative MO theory can show where bonding/anti-bonding orbitals will be in relation to each other, what it lacks it the ability to produce an accurate representation of the real MO. In terms of calculations this makes the qualitative theory not useful but it is still a useful tool in predicting MOs when programs such as Gaussian are not available.
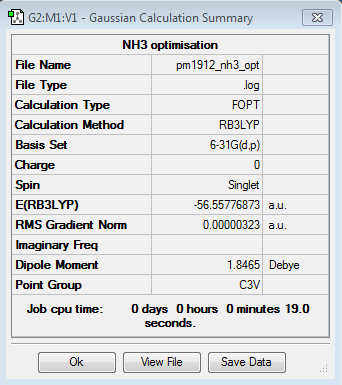
Ammonia
Optimisation Calculation
B3LYP/6-21G level
Optimisation log file here
| Summary Data | Convergence | Jmol | |||
|---|---|---|---|---|---|
 |
 |
|
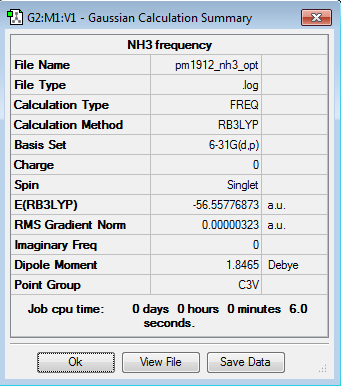
Frequency Calculation
Frequency file here
| Summary Data | Low Modes |
|---|---|
 |

|
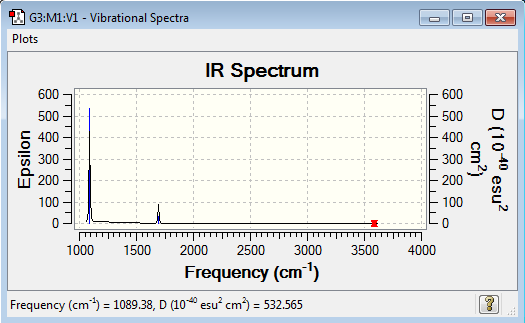
Vibrational spectrum for NH3
| Wavenumber (cm-1) | Intensity | IR Active? | Type |
|---|---|---|---|
| 1089 | 145 | yes | bend |
| 1693 | 14 | very slight | bend |
| 1693 | 14 | very slight | bend |
| 3461 | 1 | no | stretch |
| 3590 | 0 | no | stretch |
| 3590 | 0 | no | stretch |
Energy Calculation
Population file DOI:10042/93158
MO diagram
NBO Analysis
| Charge Distribution | Charge Range |
|---|---|
 |
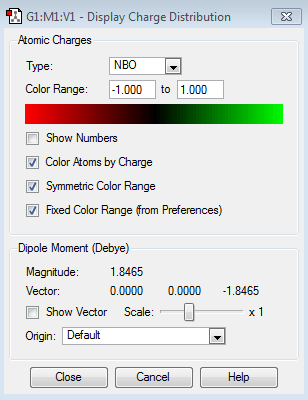
|
| Atom | Charge |
|---|---|
| Nitrogen | -1.125 |
| Hydrogen | 0.375 |
Ammonia Borane
Optimisation Calculation
B3LYP/6-21G level
Optimisation log file here
| Summary Data | Convergence | Jmol | |||
|---|---|---|---|---|---|
 |
 |
|
Frequency Calculation
Frequency file here
| Summary Data | Low Modes |
|---|---|
 |

|
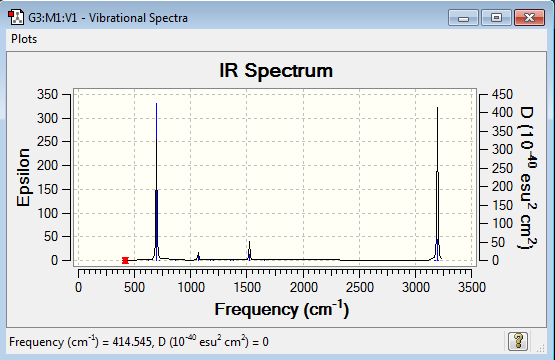
Vibrational spectrum for NH3BH3
| Wavenumber (cm-1) | Intensity | IR Active? | Type |
|---|---|---|---|
| 263 | 0 | no | bend |
| 633 | 14 | very slight | stretch |
| 638 | 4 | very slight | bend |
| 638 | 4 | very slight | bend |
| 1069 | 41 | yes | bend |
| 1069 | 41 | yes | bend |
| 1196 | 109 | yes | bend |
| 1204 | 3 | very slight | bend |
| 1204 | 3 | very slight | bend |
| 1329 | 114 | yes | bend |
| 1676 | 28 | slight | bend |
| 1676 | 28 | slight | bend |
| 2472 | 67 | yes | stretch |
| 2532 | 231 | yes | stretch |
| 2532 | 231 | yes | stretch |
| 3464 | 3 | very slight | stretch |
| 3581 | 28 | slight | stretch |
| 3581 | 28 | slight | stretch |
Molecule Energies
| Molecule | Energy (AU) |
|---|---|
| NH3 | -56.5577687 |
| BH3 | -26.6153236 |
| NH3BH3 | -83.2246889 |
Dissociation Energy (AU) = ΔE=E(NH3BH3)-[E(NH3)+E(BH3)]
ΔE = -83.2246889 -[-56.5577687 + -26.6153236] = -0.0515966 AU
Dissociation Energy (KJmol-1) = ΔE(AU)x2625.50
ΔE = -0.04 x 2625.50 = -135.47 KJmol-1
| Atomic Units | 0.0515966 |
| KJmol-1 | 135.47 |
The strength of this bond (135.47 KJmol-1) is around the same level a the iodine example (151 KJmol-1) mentioned earlier. This indicates that the association of the NH3 and BH3 molecules has a weak covalent bond strength similar to that of I2. This means the N-B bond is fairly weak on the intramolecular bonding level, but it is a lot stronger than any intermolecular bonds.
Project Section
Benzene
Optimisation Calculation
B3LYP/6-21G level
Optimisation log file here
| Summary Data | Convergence | Jmol | |||
|---|---|---|---|---|---|
 |
 |
|
Frequency Calculation
Frequency file here
| Summary Data | Low Modes |
|---|---|
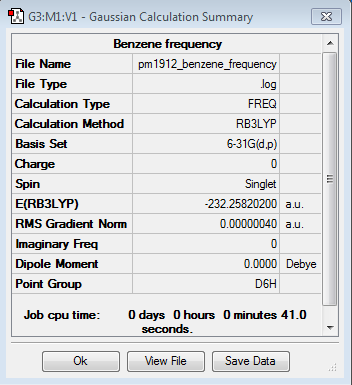 |
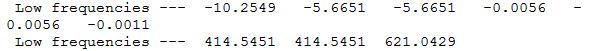
|
Vibrational spectrum for Benzene
| Wavenumber (cm-1) | Intensity | IR Active? | Type |
|---|---|---|---|
| 415 | 0 | no | bend |
| 415 | 0 | no | bend |
| 621 | 0 | no | bend |
| 621 | 0 | no | bend |
| 695 | 74 | yes | bend |
| 718 | 0 | no | bend |
| 865 | 0 | no | bend |
| 865 | 0 | no | bend |
| 975 | 0 | no | bend |
| 975 | 0 | no | bend |
| 1013 | 0 | no | bend |
| 1018 | 0 | no | bend |
| 1020 | 0 | no | stretch |
| 1066 | 3 | very slight | bend |
| 1066 | 3 | very slight | bend |
| 1180 | 0 | no | bend |
| 1203 | 0 | no | bend |
| 1203 | 0 | no | bend |
| 1355 | 0 | no | stretch |
| 1381 | 0 | no | bend |
| 1524 | 7 | very slight | stretch |
| 1524 | 7 | very slight | stretch |
| 1653 | 0 | no | stretch |
| 1653 | 0 | no | stretch |
| 3172 | 0 | no | stretch |
| 3181 | 0 | no | stretch |
| 3181 | 0 | no | stretch |
| 3197 | 47 | yes | stretch |
| 3197 | 47 | yes | stretch |
| 3208 | 0 | no | stretch |
Energy Calculation
NBO Analysis
Population file DOI:10042/98246
| Charge Distribution | Charge Range | Charge Values |
|---|---|---|
 |
 |
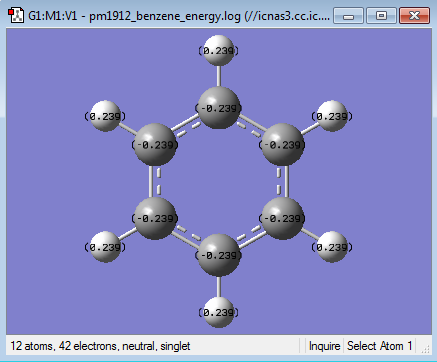
|
| Atom | Charge |
|---|---|
| Carbon | -0.239 |
| Hydrogen | 0.239 |
MO diagram
For a molecule to be aromatic it must fulfil Hückel’s Rule, it must be cyclic, planar, fully conjugated and have 4n+2 electrons. Benzene fulfils all these criteria and must therefore be aromatic. Its MOs also indicate aromaticity.
In the molecular orbital (MO) diagram there are three bonding MOs with π orbitals in the z axis projecting above and below the ring. In a linear sp2 hybridised carbon chain these would correspond to alkene carbon-carbon double bonds but in cyclic systems like benzene the carbon chain is effectively ‘joined up’ at the ends. This causes the carbon-carbon double bond to appear partially in all the carbon bonds seeming to resonate between them. Instead of forming any carbon-carbon double bond the electrons have been delocalised creating electron clouds above and below the ring. These three π MOs are the ‘electron clouds’ above and below the ring that cause aromaticity.
In the NBO analysis the σ bonding orbitals for carbon-carbon bonds and carbon-hydrogen bonds have an occupancy of 2 electrons as expected. Whereas the three π orbitals each have an occupancy of 1.66, therefore missing one third of an electron to make it agree with the formal electron occupancy of MOs. The pi electron density in these MOs is less than usual, this is because the π electrons are delocalised and can spread out more above and below the ring therefore decreasing π electron density and also adding stability as an aromatic molecule.
Boratabenzene
Optimisation Calculation
B3LYP/6-21G level
Optimisation log file here
| Summary Data | Convergence | Jmol | |||
|---|---|---|---|---|---|
 |
 |
|
Frequency Calculation
Frequency file here
| Summary Data | Low Modes |
|---|---|
 |

|
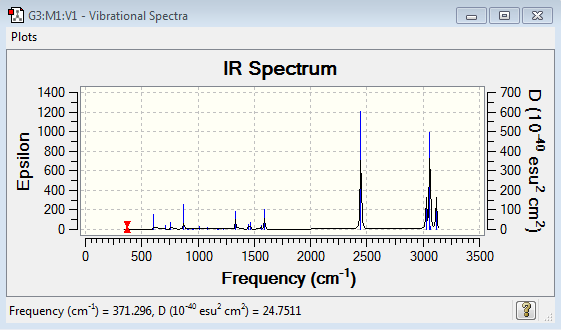
Vibrational spectrum for Boratabenzene
| Wavenumber (cm-1) | Intensity | IR Active? | Type |
|---|---|---|---|
| 371 | 2 | very slight | bend |
| 404 | 0 | no | bend |
| 565 | 0 | no | bend |
| 568 | 0 | no | bend |
| 608 | 11 | slight | bend |
| 711 | 3 | very slight | bend |
| 756 | 7 | very slight | bend |
| 815 | 0 | no | bend |
| 874 | 28 | yes | bend |
| 906 | 0 | no | stretch |
| 917 | 1 | no | bend |
| 951 | 0 | no | bend |
| 951 | 0 | no | bend |
| 961 | 2 | very slight | bend |
| 1012 | 4 | very slight | stretch |
| 1085 | 3 | very slight | bend |
| 1175 | 1 | no | bend |
| 1180 | 1 | no | bend |
| 1228 | 1 | no | stretch |
| 1333 | 31 | yes | stretch |
| 1449 | 9 | very slight | bend |
| 1463 | 14 | slight | bend |
| 1565 | 7 | very slight | stretch |
| 1592 | 40 | yes | stretch |
| 2447 | 368 | yes | stretch |
| 3027 | 108 | yes | stretch |
| 3029 | 0 | no | stretch |
| 3060 | 380 | yes | stretch |
| 3061 | 11 | slight | stretch |
| 3116 | 112 | yes | stretch |
Energy Calculation
NBO Analysis
Population file DOI:10042/98367
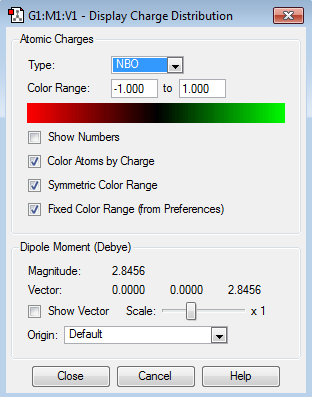
| Charge Distribution | Charge Range | Charge Values |
|---|---|---|
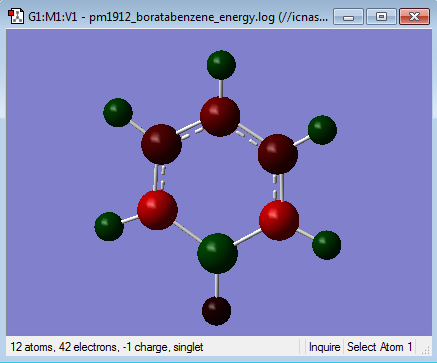 |
 |

|
Pyridinium
Optimisation Calculation
B3LYP/6-21G level
Optimisation log file here
| Summary Data | Convergence | Jmol | |||
|---|---|---|---|---|---|
 |
 |
|
Frequency Calculation
Frequency file here
| Summary Data | Low Modes |
|---|---|
 |

|
Vibrational spectrum for Pyridinium
| Wavenumber (cm-1) | Intensity | IR Active? | Type |
|---|---|---|---|
| 392 | 1 | no | bend |
| 404 | 0 | no | bend |
| 620 | 0 | no | bend |
| 645 | 0 | no | bend |
| 677 | 90 | yes | bend |
| 748 | 82 | yes | bend |
| 845 | 11 | slight | bend |
| 883 | 0 | no | bend |
| 992 | 2 | very slight | bend |
| 1006 | 0 | no | bend |
| 1022 | 4 | very slight | stretch |
| 1048 | 0 | no | bend |
| 1052 | 0 | no | bend |
| 1082 | 3 | very slight | bend |
| 1087 | 4 | very slight | bend |
| 1200 | 3 | very slight | bend |
| 1229 | 2 | very slight | bend |
| 1300 | 3 | very slight | bend |
| 1374 | 11 | slight | stretch |
| 1416 | 3 | very slight | bend |
| 1524 | 21 | yes | stretch |
| 1580 | 48 | yes | stretch |
| 1657 | 32 | yes | stretch |
| 1677 | 34 | yes | stretch |
| 3224 | 0 | no | stretch |
| 3240 | 1 | no | stretch |
| 3242 | 11 | slight | stretch |
| 3252 | 20 | yes | stretch |
| 3254 | 0 | no | stretch |
| 3570 | 158 | yes | stretch |
Energy Calculation
NBO Analysis
Population file DOI:10042/98705
| Charge Distribution | Charge Range | Charge Values |
|---|---|---|
 |
 |

|
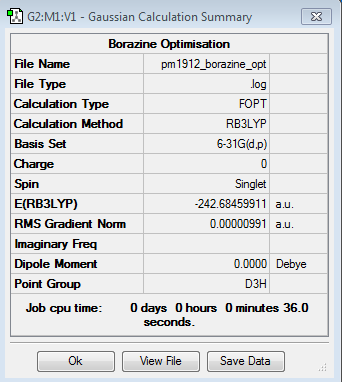
Borazine
Optimisation Calculation
B3LYP/6-21G level
Optimisation log file here
| Summary Data | Convergence | Jmol | |||
|---|---|---|---|---|---|
 |
 |
|
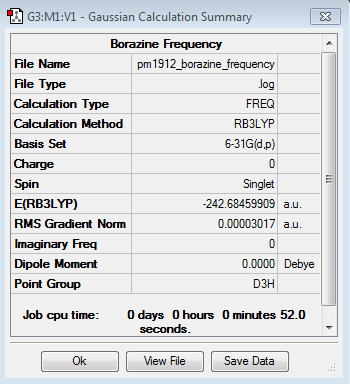
Frequency Calculation
Frequency file here
| Summary Data | Low Modes |
|---|---|
 |
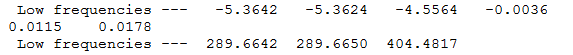
|
Vibrational spectrum for Borazine
| Wavenumber (cm-1) | Intensity | IR Active? | Type |
|---|---|---|---|
| 290 | 0 | no | bend |
| 290 | 0 | no | bend |
| 404 | 24 | yes | bend |
| 525 | 1 | no | bend |
| 525 | 1 | no | bend |
| 710 | 0 | no | bend |
| 710 | 0 | no | bend |
| 732 | 60 | yes | bend |
| 865 | 0 | no | bend |
| 928 | 0 | no | bend |
| 928 | 0 | no | bend |
| 937 | 236 | yes | bend |
| 945 | 0 | no | bend |
| 945 | 0 | no | bend |
| 945 | 0 | no | bend |
| 1052 | 0 | no | bend |
| 1081 | 0 | no | bend |
| 1081 | 0 | no | bend |
| 1246 | 0 | no | stretch |
| 1314 | 0 | no | stretch |
| 1400 | 11 | slight | bend |
| 1400 | 11 | slight | bend |
| 1493 | 494 | yes | bend |
| 1493 | 494 | yes | bend |
| 2641 | 284 | yes | stretch |
| 2641 | 284 | yes | stretch |
| 2650 | 0 | no | stretch |
| 3642 | 0 | no | stretch |
| 3644 | 40 | yes | stretch |
| 3644 | 40 | yes | stretch |
Energy Calculation
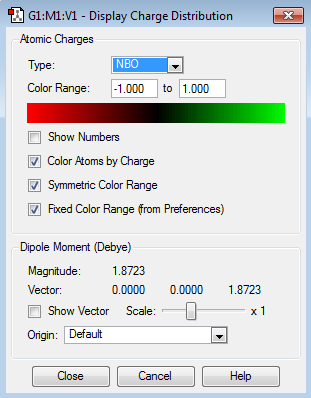
NBO Analysis
Population file DOI:10042/98926
| Charge Distribution | Charge Range | Charge Values |
|---|---|---|
 |
 |
|
Comparison of Charge Distribution
| Benzene | Boratabenzene | Pyridinium | Borazine |
|---|---|---|---|
 |
 |
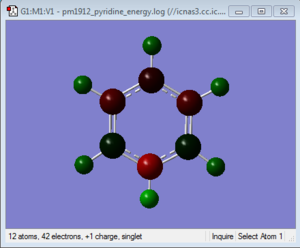 |
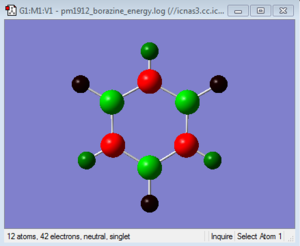
|
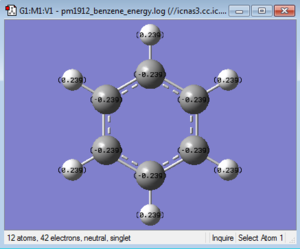 |
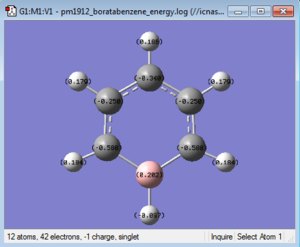 |
 |
|
The table below takes C1 and H1 from the 'bottom' carbon in the images above and moves clockwise for C2 and so on, in the case of boratabenzene and pyridinium C1 corresponds to the substituted atom.
| Molecule | C1 | C2 | C3 | C4 | C5 | C6 | H1 | H2 | H3 | H4 | H5 | H6 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
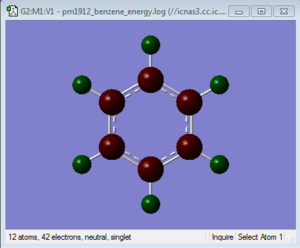
| Benzene | -0.239 | -0.239 | -0.239 | -0.239 | -0.239 | -0.239 | 0.239 | 0.239 | 0.239 | 0.239 | 0.239 | 0.239 |
| Boratabenzene | 0.202 | -0.588 | -0.250 | -0.340 | -0.250 | -0.588 | -0.097 | 0.184 | 0.179 | 0.186 | 0.179 | 0.184 |
| Pyridinium | -0.476 | 0.071 | -0.241 | -0.122 | -0.241 | 0.071 | 0.483 | 0.285 | 0.297 | 0.292 | 0.297 | 0.285 |
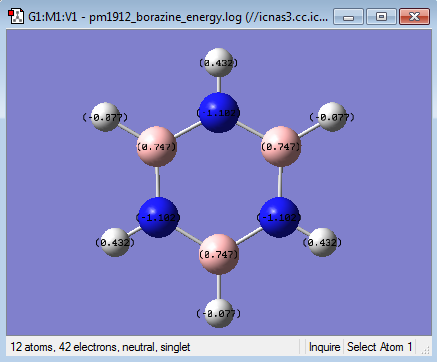
| Borazine | 0.747 | -1.102 | 0.747 | -1.102 | 0.747 | -1.102 | -0.077 | 0.432 | -0.077 | 0.432 | -0.077 | 0.432 |
It is important to note that the electronegativity of an atom depends on its effective nuclear charge and electron shielding. Generally electronegativity increases towards the top right of the periodic table due to increased effective nuclear charge and decreased electron shielding.
In benzene all the charges on the carbons are equal as is the case with all the hydrogens. This is due to the symmetry and two elemental component nature of the molecule. As carbon is more electronegative than hydrogen it draws electron density towards it more and therefore has a slight negative charge of -0.239. As the molecule has no charge and is neutral the charge in the hydrogens is 0.239, the sum of all the charges is therefore 0.
In boratabenzene a carbon atom is replaced with a boron atom and a negative charge is added to the molecule. The result is that the sum of all the individual charges will add up to a charge of -1 overall. Boron is in group 3 of the periodic table and is less electronegative than carbon so will have less share of the electron density. This means that the boron atom (C1) has a positive charge of 0.202, this electropositivity results in the hydrogen atom (H1) attached to the boron having a very slight negative charge of -0.097 being almost neutral. Compared to the rest of the hydrogens in the molecule this negative charge is quite different as the rest are in a charge range of 0.179-0.186, all about 0.060 lower in charge than the hydrogens in benzene, this is due to the overall negative charge. The carbons adjacent to the boron, in the ortho position, have quite a negative charge of -0.588 whereas the carbons in the meta position have a charge of -0.250 similar to that of the charges of the carbon atoms in benzene. The carbon opposite born in the para position has a charge of -0.340. This is because the electropositivity of boron has a greater effect on the ortho and para positions, the first because it is directly adjacent to it and the second because electron density is moved over the ring in the electron cloud.
The situation in pyridinium is effectively the opposite of the charge distribution in boratabenzene compared to benzene. As one carbon atom has been replaced by a nitrogen and a positive charge added the sum of all the individual charges will add up to an overall charge of 1. Nitrogen is in group 5 of the periodic table and is therefore more electronegative than carbon. As a result it has a charge of -0.476 and pulls electron density away from other atoms making them more positive. The hydrogen attached to the nitrogen has an increased positive charge of 0.483, while the rest of the hydrogens have a charge in the range 0.285-0.297 similar again to the other values on different molecules. Again the same ortho para directing effect of charge distribution is present again with the adjacent carbons having a positive charge of 0.071. At the para position the carbon has a more negative charge of -0.122 and the most negative carbons being at the meta position with a charge of -0.241. This is due to the electronegativity effects over the electron cloud above and below the ring.
Borazine has three B-N units and as before the boron atoms are more electropositive while the nitrogen atoms are more electronegative. As this molecule is more symmetric than the previous two the charges on each boron are equal as is the charges on each nitrogen. The same can be said about the hydrogens. The boron atoms are more electropositive so have a positive charge of 0.747. This is a greater charge than in boratabenzene because nitrogen is more electronegative than carbon so electrons density is pulled away more at both ortho and para positions. The reverse is true nitrogen having a negative charge of -1.102 it is more negative than in pyridinium and it is able to pull more electron density from the boron atoms in the ring due to its higher electronegativity. The hydrogens attached to boron have a charge of -0.077 which is similar to that of the hydrogen adjacent to boron in boratabenzene. The reason for this is that the rest of the atoms in the ring do not have a great effect on the charge distribution between hydrogen and its adjacent atom. This is the same case for the hydrogens attached to nitrogen win the fact that they have a positive charge of 0.432, again similar to that in pyridinium. The symmetry in charge in this molecule means that the sum of all the individual charges add up to a total overall charge of 0 making it neutral.
| Molecule | Pauling Electronegativity |
|---|---|
| Carbon | 2.25 |
| Hydrogen | 2.20 |
| Boron | 2.04 |
| Nitrogen | 3.04 |
Comparison of MOs
| Benzene | Boratabenzene | Pyridinium | Borazine | |
|---|---|---|---|---|
| MO | 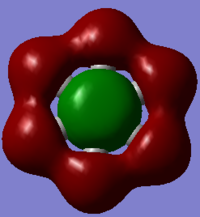 |
 |
 |

|
| LCAO |  |
 |
 |
|
| Energy (AU) | -0.51787 | -0.28949 | -0.79009 | -0.55137 |
| Order | 12th | 12th | 12th | 10th |
| Degenerate | No | No | No | No |
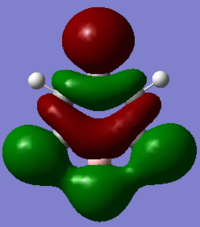
In the above benzene MO carbon sp2 orbitals are bonding with hydrogen s orbitals, they are all in phase forming a ring of through space bonding between all of the hydrogens. Inside this ring of electron density are the other ends of the carbon sp2 orbitals forming an electron density in the other phase. It is not degenerate and is quite low in the MOs (12th) as it has an energy of -0.51787.
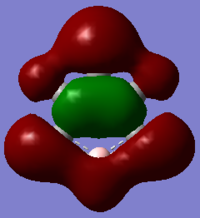
In the MO for boratabenzene the electron ring seen before has been broken in two places as a result of no through space bonding of two pairs of hydrogen. This will be due to the substituted boron atom that is electropositive so pushed electron density away from it. This increases the electron density in the middle of the molecule and breaks the ring of the other phase. As boron is electropositive the energy of the MO has increased to -0.28949 but the MO is in the same position of 12th in the order. Similarly to benzene all the hydrogen atoms are contributing to the MO and there is a centre of electron density in the middle of the ring.
For pyridinium the MO again has a break in the through space bonding of the hydrogens. This time it is at the para position to the nitrogen where the hydrogen is not contributing to the MO. This is because nitrogen is electronegative and so pull electron density away from the rest of the components of the molecule. This depletes the electron density around the far hydrogen so it is unable to interact with any orbitals. As nitrogen is electronegative the energy of the MO has decreased to -0.79009, but the MO is still on 12th position in the order of the MOs. Again the centre area of electron density is kept.
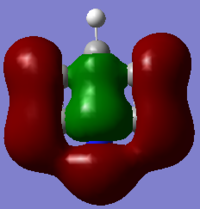
The hydrogen contribution in borazine is quite different to that in benzene. Only the hydrogens attached to the nitrogen atoms contribute to the MO, this is because nitrogen is electronegative while boron is electropositive. This means that nitrogen pulls electrons away from the hydrogen s orbital forcing it to bond, while boron pushes the hydrogens electrons into its s orbital so it takes no part in the orbital interactions. The result of this is that there is no form of through space bonding ring as seen before. Instead there are more clear orbitals including the central electron density. As the electronegativity and electropositivity of nitrogen and boron almost cancel out each other the energy is very similar to that of benzene being at -0.55137. Interestingly the order of this MO has changed from 12th to 10th. This is because two degenerate s MOs have been raised in energy above the MO shown above.
| Benzene | Boratabenzene | Pyridinium | Borazine | |
|---|---|---|---|---|
| MO | 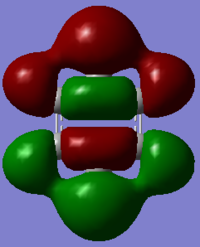 |
 |
 |

|
| LCAO |  |
 |
 |
|
| Energy (AU) | -0.41653 | -0.16885 | -0.66589 | -0.43403 |
| Order | 16th | 16th | 15th | 14th |
| Degenerate | Yes | No | No | Yes |
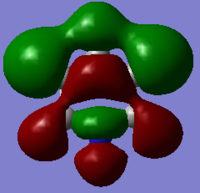
In the benzene MO above the bonding is similar to the previous example in which sp2 carbon orbitals are bonding with s hydrogen orbitals. The difference is that half of the bonds are in the other phase. Therefore of course it has a higher energy of -0.4653 which places it higher in order at 16th. It is also a degenerate orbital so has the same energy value as the 15th MO. There is through space bonding through each triplet of hydrogens on each side of the molecule. The result is that there are three nodal planes in that axis with two different phases in the centre of the ring.
In boratabenzene the boron side of the MO has not changed much compared to the benzene MO. But at the other end of the molecule it appears that the two carbons and hydrogens meta to the boron have stopped contributing to the MO. This will be due to the electropositivity of the boron atom as it pushes electrons across the ring into these carbons and into the hydrogens forcing their electrons to remain core to the atom. The carbon and hydrogen para to the boron still contribute to the MO which keeps the three nodal planes in that axis. Again as is the trend in boratabenzene, the energy of the MO has increase to -0.16885 and the order is the same. However, whereas the benzene MO was degenerate, this MO has lost degeneracy. This again is due to the substituted boron atom as it makes the molecule unsymmetrical and so the orbitals also lose their symmetry and therefore degeneracy.
In pyridinium the electronegativity of nitrogen has pulled electrons away from the hydrogen through space bonds on its side of the molecule resulting in a smaller more dense hydrogen s orbital bonding to the nitrogen sp2 orbital. The two hydrogens meta to the nitrogen now bond through space with the same phase electron density in the centre of the ring, while the orbitals on the other side of the molecule remain very similar to benzene. Again due to the presence of nitrogen the energy has decreased to -0.66589 and it is not a degenerate MO like in boratabenzene. Interestingly the position in the MO order for the pyridinium MO has changed from 16th to 15th. It has changed order with the other degenerate orbital in benzene. This makes sense because the addition of an electropositive atom makes one of the degenerate MOs slightly more stable than the other while the addition of an electronegative atom makes the other MO slightly more stable than the other. Hence the reverse in order.
The MO arrangement in borazine is quite similar to that in boratabenzene, but the hydrogens that were not contributing in boratabenzene are contributing in borazine. This still keeps the three nodal plane structure and this band of orbital phase which these hydrogen s orbitals are contributing too forms a curve of electron density around the other phase which is located around a nitrogen atom due to the electronegativity of it. Again the charge of -0.43403 of this MO is similar to that of benzene as it has no overall charge. Also as it is a more symmetric molecule than either boratabenzene or pyridinium it is degenerate like benzene. It is degenerate with MO 13 in the order while it is number 14. This is a change in the order from the other molecules. This is because borazine is a totally different molecule to benzene and the orbital contributions from nitrogen and boron are different to that of carbon, ergo changing the order of the MOs. What has happened in this case is that the two MOs below this MO in benzene (a totally s orbital contributing MO and a totally sp2 contributing MO) have moved up in energy to above this MO in borazine hence meaning it is 14th in the order.
| Benzene | Boratabenzene | Pyridinium | Borazine | |
|---|---|---|---|---|
| MO |  |
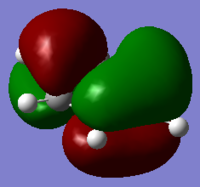 |
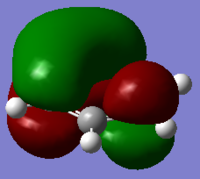 |

|
| LCAO | 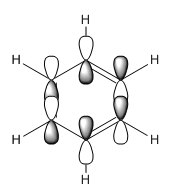 |
 |
 |
|
| Energy (AU) | -0.24690 | -0.01094 | -0.50847 | -0.27593 |
| Order | 21st | 21st | 20th | 21st |
| Degenerate | Yes | No | No | Yes |
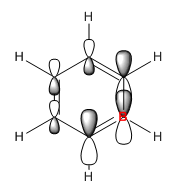
In benzene the π orbitals project electron density above and below the ring. Half are in phase and the other half in the other phase. This gives the image of four areas of electron density, two below and two above the ring. These π MOs contribute to what makes benzene aromatic. The energy of the MO is -0.24690 and it is degenerate with the 20th orbital itself being the 21st.
In boratabenzene boron is electropositive so therefore pushes electrons away from it, this makes the electron cloud around it larger and more diffuse, while the orbitals in the other phase are smaller and denser. The addition of boron again breaks the degeneracy but the MO remains 21st in the order. It has a more positive energy of -0.01094 due to the addition of boron and the overall negative charge.
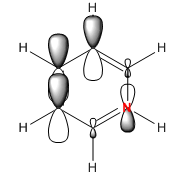
Again in pyridinium the opposite happens to that in boratabenzene, the nitrogen pulls electron density towards it so that orbital phase is smaller and desner while as a result the other phase is able to spread out and become a larger and more diffuse electron cloud. The addition of nitrogen makes the MO more negative at an energy of -0.50847. Again degeneracy is broken but as before the order is reversed and this MO is 20th in order.
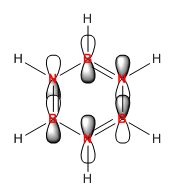
In borazine one of the π orbital phase is over and below two boron atom and one nitrogen atom while the other phase is over and below two nitrogen atoms and one boron atom. This acts similar to boratabenzene and pyridine. The electron over the two nitrogen’s experience more electronegativity so their cloud becomes smaller and denser. Meanwhile the electrons over the two boron experience more electropositivity and are pushed away making their orbital larger and more diffuse. This gives a similar shaped MO to the rest of the molecules. Its energy is again similar to that of the benzene MO at an energy of -0.27593 and it is also 21st in order and degenerate.
Effect of Substitution on the MO diagram
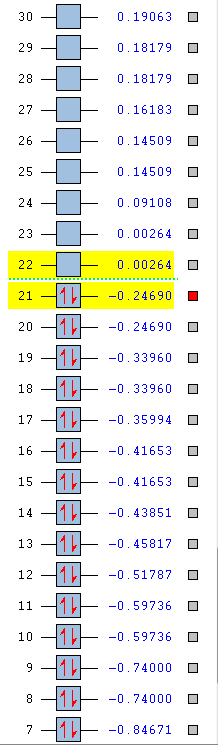
The addition of these substituents will affect the energies of the entire MO diagram. The boratabenzene carries a negative charge so the overall energy will be lower and more stable because it is more electron rich. Meanwhile in pyridinium the molecule carries a positive charge so is therefore electron poor, less stable and higher in energy. Benzene and borazine are both neutral molecules so will have similar energies as shown in the comparison above.
The order changes with the addition of new atoms that is why the order of MOs for boratabenzene and pyridinum is fairly similar to benzene while for borazine it is quite different. It has a larger variety of atoms that change the relative energies of the MOs and hence the order.
The addition of one substituent to make boratabenzene and pyridinium breaks the symmetry of the molecule seen in benzene and borzazine. When this happens the orbitals eigenvalues change and hence the energies also change. That is why boratabenzene and pyridinium have no degenerate orbitals while benzene and borazine do. The ordering and relative energies of the MOs can be seen below.
| Benzene | Boratabenzene | Pyridinium | Borazine |
|---|---|---|---|
 |
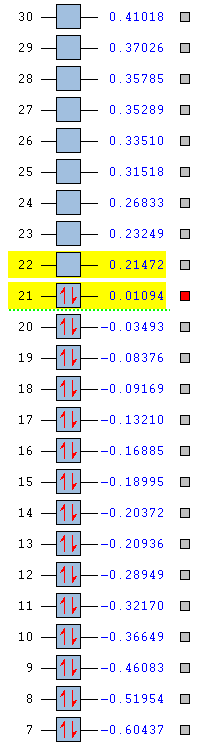 |
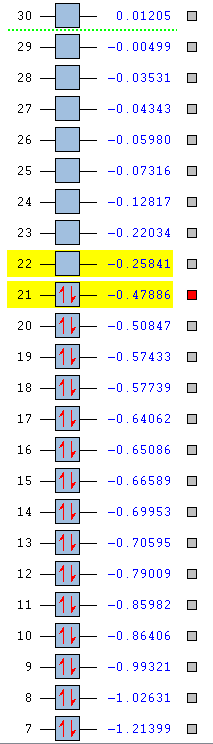 |
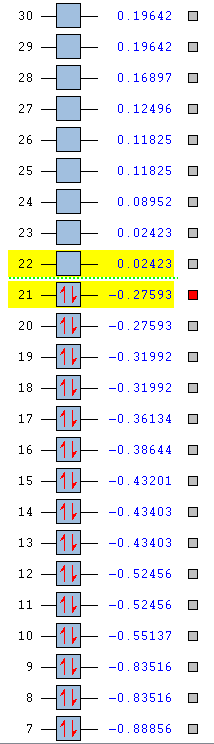
|
References
Shriver and Atkins' Inorganic Chemistry, Fifth Edition © 2010 P.W. Atkins, T.L. Overton, J.P. Rourke, M.T. Weller, and F.A. Armstrong