Rep:Mod:PhysBE411

Physical Module: Transition States and Reactivity

Computational methods can be used to study reaction pathways and more specifically transition states. In this experiment the Cope rearrangement reaction and Diels-Alder cycloaddition reaction are used as examples of this. Using various methods the lowest energy conformation of 1,5-hexadiene can be found as well as the conformation that exists as a reactant in the Cope rearrangement reaction. The two possible transition states of this reaction can be studied and their activation energies calculated to gain some understanding of the mechanism of this reaction. The Diels-Alder cycloaddition will also be studied. The origin of the symmetry allowed reaction between ethene and cis-butadiene will be visualized and the reaction between maleic anhydride and hexa-1,5-diene studied in terms of the regioselectivity of its two conformational different transition states.

The Cope Rearrangement Tutorial

The Cope rearrangement is a specific [3,3] sigmatropic rearrangement in which a sigma bond moves and the pi system is redistributed across the molecule. In this case the Cope rearrangement of hexa-1,5-diene is considered with regard to its conformations and the boat and chair forms of its reaction's transition state.

Optimizing the Reactants and Products

Conformation of 1,5-hexadiene

The Conformations of 1,5-Hexadiene

1,5-hexadiene is one of the simplest precursors in the Cope rearrangement. The three rotating carbon-carbon bonds within the center of the molecule cause there to be 10 energetically different conformations, when taking into account enantiomers and symmetry.

Within these conformations you would expect that where two carbons are in the eclipsed form (F-J) the conformer will be of higher energy than conformers with CH-eclipsed bonds (A-E). This is demonstrated in the case of butane where the difference in energy between the CC eclipsed form and the CH eclipsed form is 1.5kcal/mol. The energies of these forms can be optimized by computational methods in order to find the most suitable candidates for the reactants and products in the Cope Rearrangement reaction.

The table below shows the total energy for all energetically distinct conformers of the molecule, it shows that in the case of this molecule the anti conformer is generally of higher energy. Relating these structures to the literature, the energies found are all in line with the energies expected, as is also the case with the point groups.

The lowest energy conformation is the Gauche Conformer D (-231.69266Hartrees) this maybe due to an attractive interaction between the pi orbital of the double bond and the neighboring proton, whose orbital would interact with that of the pi bond. This conjugation will stabilize the molecule making it lower in energy. The highest energy conformer of the CH eclipsed forms is C (-231.69153Hartrees) this maybe explained by interactions between the two alkene protons which are 2.51A apart. This proximity will have a repulsive effect increasing the overall energy of the molecule.

Optimized Energies for the Anti and Gauche Conformations of 1,5-Hexadiene (Relating to the Instructional Wiki)

	Conformer A - Gauche2	Conformer B - Anti1	Conformer C - Gauche4	Conformer D - Gauche3	Conformer E - Anti2	Conformer F - Gauche6	Conformer G - Anti4	Conformer H - Gauche5	Conformer I - Gauche1	Conformer J - Anti3
Total Energy/Hartrees	-231.69167	-231.69260	-231.69153	-231.69266	-231.69254	-231.68916	-231.69097	-231.68962	-231.68772	-231.68907
Point Group	C2	C2	C2	C1	Ci	C1	C1	C1	C2	C2h
Dihedral Angle (C2-C3-C4-C5)	64.17	-176.91	-63.65	67.70	-179.996	70.23	-178.32	-71.09	75.76	-179.98

Analysis of Conformer E

Further Analysis of Conformer E was done at a higher basis set in order to get an even better approximation for its lowest energy conformation. An optimization calculation was run as before at the B3LYP/6-31G(d)level of theory.

Optimised Conformations of Conformer E using the HF/3-21G and B3LYP/6-31G(d) Basis Sets

Anti 2 Conformation at HF level of Theory	Anti 2 Conformation at B3LYP level of Theory

Geometrical Features of Conformer E Optimized Under Different Basis Sets

Basis Set	Bond Length			Angle
	C1-C2	C2-C3	C3-C4	C1-C2-C3	C2-C3-C4	C2-C3-C4-C5
HF/3-21G	1.32	1.51	1.55	179.996	124.81	111.35
B3LYP/6-31G(d)	1.33	1.50	1.55	180	125.29	112.68

IR Spectrum of Conformer E

This shows that the geometries of the results of the two different approaches don't differ wildly, the bond lengths especially are very similar, however there is some deviation between their angles.

Following on from this a frequency calculation was run using the same higher level of theory (B3LYP/6-31G(d)). This calculation can be used to confirm that this conformation is of a minimum energy by the absence of an imaginary vibrational frequency. The infrared spectrum of the molecule can be generated from the molecular vibrations and compared to literature.

The thermochemical energies for this molecule can be found in the output file of the calculation:

Sum of electronic and zero-point Energies=           -234.46921 Hartrees
Sum of electronic and thermal Energies=              -234.46186 Hartrees
Sum of electronic and thermal Enthalpies=            -234.46091 Hartrees
Sum of electronic and thermal Free Energies=         -234.50082 Hartrees

The various information above can be used to consider the potential and free energy of the system. The sum of the electronic and zero-point energies (E= E_elec + ZPE) show the potential energy at 0K and the sum of electronic and thermal energies (E = E + E_vib + E_rot + E_trans) considers it at 298.15K and 1atm. The sum of electronic and thermal enthalpies (H = E + RT) shows the enthalpy of the system containing a correction for thermal energy and the sum of electronic and thermal free energies ( G= H - TS) suggests the entropic contribution to the free energy of the system.

This data shows that the energy at 0K is lower than that at room temperature, this is as expected because at 0K there will be no internal movement of the molecule and hence no contribution from vibrational, rotational or translational energies.

Optimizing the "Chair" and "Boat" Transition Structures

Conformer E was considered for this reaction and used to model both the chair and boat transition states for the Cope rearrangement reaction. A number of different ways of optimizing the geometry of the transition states were considered including using redundant coordinates and QTS2(TS)optimization and frequency calculation.

Chair Transition State

The chair transition state was constructed from two allyl fragments. Firstly the geometry of a single allyl fragment was optimized using the HF/3-21G level of theory giving an energy of -117.61330Hartrees. Two allyl fragments are placed 2.2A apart and then using this as a guess for the transition state, the molecule is then optimized in two different ways.

Cope Rearrangement Chair Transition State Vibration

Firstly it can be optimized using a opt + freq calculation to a TS using the Berny Method. By calculating the force constant once an imaginary vibration can be found. The imaginary vibration was found at 817.95cm^-1 (expected value of 818cm^-1) on animation it can be seen that this corresponds to the coming together of the two terminal carbons on each allyl molecule, the movement expected during this reaction. In this case the total energy is -231.61932Hartrees.

Chair Transition State by Redundant Coordinate Method

Secondly the transition state was optimized by freezing the reaction coordinate in order to minimize the rest of the molecule first and then unfreezing it in order to find the minimum for the transition state. This means that the force constant Hessian matrix doesn't need to be calculated and therefore is a faster method of computing the transition state.

By looking at the atom distances between the bond that will be formed the suitability of both of these methods to find the true transition state can be studied. All the measured geometric parameters were identical in both versions of the transition state, namely the intranuclear bond lengths was 1.39A, the internuclear distance between the two allyl molecules is 2.02A and the angle within the each molecule is 120.05^o. This suggests that both methods for determining the transition state are equally effect from the same guess input file. It also confirms that the guess structure was close to the exact structure as the first method was as successful in calculating the force constants as the second which doesn't need to calculate them.

The Boat Transition State

The boat transition state was constructed in much the same way as the chair using two pre-optimized allyl fragments, placing them together in the correct geometry and setting them to 2.2A apart. In the case of the boat transition state the QTS2 method was used to optimize the energy. By ensuring that the same labeling system is used in the reactants and products, an optimization and frequency calculation was run that could help define the geometry of the boat transition state. This calculation was run with a predicted transition state with a dihedral angle (C2-C3-C4-C5) of 0^o and inside C2-C3-C4 and C3-C4-C5 angles of 100^o.

Cope Rearrangement Boat Transition State Vibration

The result of this calculation shows the boat transition state with a single imaginary vibration of -840nm and energy of -231.60280Hartrees. Visualizing this vibration shows that it corresponds to the coming together of the two terminal carbons and the separation of the two central carbons. This is the expected vibration seen during the Cope rearrangement. The QTS2 method is advantageous because it is fully automated however it required a good starting guess for the transition state and therefore a lot of permutations of structure, in the input file, were needed for a successful calculation.

Summary Table of the Energies of the Two Transition States

Transition State	Energy
	Berny TS	Redunant Coordinates	QTS2 (TS)
Chair	-231.61932	-231.61932
Boat			-231.60280

The Reaction Pathway

The reaction pathway can be studied through both the minimum energy position on its potential energy surface and the activation energies of the two transition states.

IRC

IRC Energy Plot of the Chair Transition State

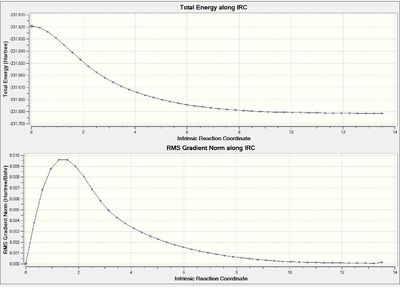
An intrinsic reaction coordinate (IRC) was run as it can be used to determine the minimum energy pathway from the transition state to its local minimum by using many points along the pathway to the point where the energy plateaus. The IRC in this case has been run in the forward direction only and the force constants calculated at every step.

The lowest energy conformation is achieved after 44 steps. The structure of the first and final conformations can be compared by considering their different geometry and energy. The IRC determines the minimum energy conformation and therefore the energy of step 44 (-231.69158Hartrees) is, as expected, lower than that of the first step (-231.61932Hartrees), this confirms that the calculation has found a minimum. The most noticeable different between the two conformations is the bond symmetry, in step 1 the bond lengths within each molecule were identical (1.39A) and the distance between the two molecules is the same (2.02A) for both sets of terminal carbons. However in step 44 the bond lengths within each molecule are different in preparation for the formation of two different types of bonds - single and double - this means one bond is shorter than the other (1.32 and 1.51A). As well as this difference in intranuclear distances there is also a difference in the internuclear distances as the one end approaches much closer (1.55 and 4.23A) almost within the van der Waals radius of the carbon atom as it prepares to form a new bond whereas the other distance is much larger as there is no bond formation at those carbons.

Structures of Steps 1 and 44 in the Determination of the IRC of the Chair Transition State

Activation Energies

In order to determine the activation energy of the reaction via the two different transition states a higher level of theory needed to be used. The B3LYP/6-31G(d) was used to optimize the two transition states to a minimum. Comparing this to the activation energies obtained at the lower level of theory and literature values shows the large difference in the energies obtained at each level of theory. The Energies at 0 and 298.15K were then found by running a frequency calculation, using the same basis set, on the optimised structure and checking the sum of the electronic and zero-point (0K) and sum of electronic and thermal energies (298.15K).

Geometrical Features of the Reactant, Boat and Chair Transition States

	Reactants		Chair Transition State		Boat Transition State
	Reactants Optimized at HF/3-21G Theory	Reactants Optimized at B3LYP/6-31G(d) Theory	Chair Transition State Optimized at HF/3-21G Theory	Chair Transition State Optimized at B3LYP/6-31G(d) Theory	Boat Transition State Optimized at HF/3-21G Theory	Boat Transition State Optimized at B3LYP/6-31G(d) Theory
Basis Set	HF/3-21G	B3LYP/6-31G(d)	HF/3-21G	B3LYP/6-31G(d)	HF/3-21G	B3LYP/6-31G(d)
Intramolecular Bond Lengths/A	1.32, 1.51	1.33, 1.50	1.39	1.41	1.38	1.39
Intermolecular Bond Lengths/A	1.55	1.55	2.02	1.97	2.14	2.21
Dihedral Angle/o	179.996	180	54.96	54	0	0

In the reactants the higher level of theory shows a tightening of the dihedral angle to exactly 180^o as well as a shortening of the single bonds and lengthening of the double bonds within the molecule. This acts to bring the bond lengths within the molecule closer to the expected bond lengths of 1.47 and 1.54A. Within chair transition state the same effect can be seen, increasing the dihedral angle and double bond length and decreasing the single and intermolecular bond distances.

Electronic Energies and Energies of the Boat and Chair Transition States at 0K

	Electronic Energy/Hartrees		Sum of Electronic and Zero-Point Energies		Activation Energy/Hartrees		Activation Energy/kcalmol-1		Expected Activation Energy/kcalmol-1
Basis Set	HF/3-21G	B3LYP/6-31G(d)	HF/3-21G	B3LYP/6-31G(d)	HF/3-21G	B3LYP/6-31G(d)	HF/3-21G	B3LYP/6-31G(d)
Boat Transition State	-231.60280	-234.54309	-231.45093	-234.40234	0.08861	0.06687	55.60	41.96	44.7 ± 2.0
Chair Transition State	-231.69167	-234.55698	-231.46669	-234.41488	0.07286	0.05433	45.72	34.09	33.5 ± 0.5

The activation energies were calculated with reference to the conformer E energies as the reactant ( At 0K HF/3-21G = -231.53954 and B2LYP/6-31G(d) = -234.46921Hartrees, At 298.15K HF/3-21G = -231.53257 and B2LYP/6-31G(d) = -234.46186Hartrees ).

Energies of the Boat and Chair Transition States at 298.15K

	Sum of Electronic and Thermal Energies		Activation Energy/Hartrees		Activation Energy/kcalmol-1		Expected Activation Energy/kcalmol-1
Basis Set	HF/3-21G	B3LYP/6-31G(d)	HF/3-21G	B3LYP/6-31G(d)	HF/3-21G	B3LYP/6-31G(d)
Boat Transition State	-231.44530	-234.39599	0.08727	0.06587	54.76	41.33	41.32
Chair Transition State	-231.46133	-234.40895	0.07124	0.05291	44.70	33.20	33.17

From this it is clear why a higher level of theory is needed. The energies calculated at the B3LYP/6-31G(d) level yield much more accurate activation energies that those at HF/3-21G. In both cases this increase in accuracy has brought the activation energies significantly closer to the expected values.

The activation energy of the Chair transition state is a good match for that in the literature and is very close to the boundaries of error given. When comparing this to the energy obtained at the lower level of theory there is a much greater difference and therefore illustrates the ability of the higher level of energy to calculate a much more accurate transition state.

Diels-Alder Cycloaddition Reaction

The Diels-Alder cycloaddition reaction is a pericyclic reaction that occurs between two pi systems, a diene and a dienophile, in order to form a cyclohexene. It offers good regio- and stereo-selective control that can be extended to other conjugated systems.

In this experiment the reaction between cis butadiene and ethene will be studied in order to determine the symmetry of both the reactant and product molecular orbitals, as well as the geometry of the reaction's transition state. The regioselectivity of the reaction will also be looked at into order to determine the preferred product of the reaction, endo or exo.

Cis-butadiene

Cis-butadiene will be used as the diene in this studied reaction with ethene. Its geometry was first optimized using the HF/3-21G level of theory. The final energy of the product was -154.05514Hartrees. The molecular orbitals of the optimized structure can be modeled and used further to look at the electronic contribution of the diene to the final molecule.

Images of the Molecular Orbitals of Cis-Butadiene

The HOMO orbital of the molecule is asymmetric. The nodes in the molecule fall between the red and green lobes of the HOMO. This shows the two separate pi systems within the molecule, but the proximity of the two systems suggests that the molecule could be fully conjugated.		The LUMO orbital of the molecule is symmetric. It shows the pi* orbitals of the two pi systems and the conjugation of these across the central single bond. The nodes fall within the plane of the molecule and between the double bonds of the molecule suggesting that for this orbital there is no conjugation over the double bonds.

The Transition State

A number of methods, that had previously been discussed above for the Cope rearrangement reaction, were considered to optimize the transition state of this reaction. However it was decided to use a method previously used in optimizing the chair transition state of 1,5-hexadiene due to it's simplicity and that a good guess for the transition state could be made initially.

Firstly the reactants were optimized separately under the HF/3-21G level of theory. Then the two molecules were combined in an envelope like geometry and the internuclear distances between the two molecules set to 2.2A in order to give a best guess for the transition state. An optimization and frequency calculation was then run, optimizing to a transition state using the Berny method, calculating the force constants only once.

The Structure and Molecular Orbitals of the Diels-Alder Transition State

	1,5-hexdiene formation transition state
HOMO	The transition state for the Diels-Alder reaction between ethene and cis-butadiene has an energy of -231.60321Hartrees	LUMO

Imaginary Vibration of the Diels-Alder Transition State

Lowest Energy Positive Vibration of the Diels-Alder Transition State

This gave a good approximation for the transition state with the imaginary vibration, of -817.71cm^-1, showing the two molecules approaching each other in a synchronous motion. Comparatively the lowest positive vibration at 166.54cm^-1 is an asynchronous rocking motion that does not contribute to the coming together of the two molecules.

Predicted IR Spectrum of the Diels-Alder Transition State

The justification of calling this the transition state is also shown in the final bond lengths between the two molecules, the length of approach is 2.21A. Typically an sp3-sp3 carbon bond length is 1.54A and for a sp2-sp2 carbon it is 1.47Athis suggests that a bond has not been fully formed in the transition state. However it is within the van der Waals radius of the carbon atom, which is 1.7A so a partial bond may have started to form at this point in the reaction.

Looking at the HOMO and LUMO orbitals for the reactants there is a clear contribution from both to the molecular orbitals of the transition state, this is especially the case for the ethene molecule. The visualization of the HOMO orbital throws some doubt onto the final structure obtained however considering the imaginary vibration is as expected, it can be assumed that this is a form of the transition state, if not the most minimal energy one. Further calculations were run in order to find the transition state with the correct HOMO orbital however it could not be found with the correct geometry and imaginary vibration.

The Molecular Orbitals of Ethene and Cis-Butadiene

Ethene				cis-butadiene
HOMO - Symmetric		LUMO - Asymmetric		HOMO - Asymmetric		LUMO - Symmetric

The reactants orbitals above display frontier molecular orbital theory. The HOMO of cis-butadiene and the LUMO of ethene are of correct symmetry to interact to form a bonding molecular orbital in the product. This means that the reaction is symmetry allowed and therefore no other conditions are needed, such as light, in order for the reaction to proceed.

Regioselectivity

The reaction can form two different products depending on the transition state. The exo product is formed when the approach of the maleic anhydride occurs with the oxygens pointing away from the double bond, and the endo product is formed when the oxygens point towards it. In order to determine the energies of the transition states first the reactants were optimized separately and then together using the HF/3-21G level of theory. Then the endo and exo products were optimized the same way. The transition state was found using the QTS2 method, an Opt+Freq calculation under the HF/3-21G level of theory, this gave an optimized version of each transition state. This was used in order to utilise the reactants and products to find the transition state as the initial guess for the transition state was not a confident enough one.

The imaginary vibrations of these transition at -647.54 and -643.32cm^-1 for the exo and endo transition states respectively. These vibrations show the coming together of the reactant molecules to form the product as is expected. These Transition state structures were then optimized under a higher level of theory in order to obtain a more accurate energy, and the HOMO and LUMO orbitals of each visualized.

Imaginary Vibration of the Exo Transition State

Imaginary Vibration of the Endo Transition State

The Energies of the Exo and Endo Transition States under the B3LYP/6-31G(d) Level of Theory

	Exo Transition State	Endo Transition State
	EXO Transition state at the B3LYP/6-31G(d) level of theory	ENDO Transition state at the B3LYP/6-31G(d) level of theory
Total Energy/Hartrees	-612.66122	-612.68340
Sum of Electronic and Zero-Point Energies/Hartrees	-612.47669	-612.50214
Sum of Electronic and Thermal Energies/Hartrees	-612.46612	-612.49179
Activation Energy at 0K/kcalmol-1	34.90	18.93
Activation Energy at 298.15K/kcalmol-1	33.58	17.47
Dihedral Angle/o	-169.56	-175.67
Intermolecular Bond Lengths/A	1.5	2.27

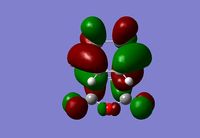
Activation energies were calculated by comparing the energy of the transition state to the energy of the reactants (At 0K B3LYP/6-31G(d) = -612.53231, At 298.15K B3LYP/6-31G(d) = -612.51964). The endo product should be the kinetic product, this is shown by its much lower activation energy. The exo product has a tighter dihedral angle than the endo, this is due to the repulsion between the two reactants as seen in the HOMO of the exo transition state below.

The HOMO and LUMO Molecular Orbitals of the Exo and Endo Transition States

Exo Transition State		Endo Transition State
HOMO	LUMO	HOMO	LUMO

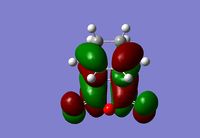The endo and exo products will be stabilised by secondary orbital overlap (SOO). This is the mixing of the HOMO orbital of one reactant with the LUMO orbital of the other. This can be seen in both transition state HOMO orbitals above. In the case of the endo transition state the orbitals from the central oxygen shows a node around it, the orbitals on that oxygen are of the same symmetry and hence will interact with the orbitals from the double bond that is formed in the product above it. For the exo transition state the position of the oxygen and double bond are much separated and therefore there is no SOO. This SOO effect in the endo transition state, and hence the greater stabilisation, is a reason that the energy of the endo transition state is lower than that of the endo.

Conclusion

These reactions have shown the usefulness of molecular modelling in the visualization and analysis of transition states. A wide range of methods for optimizing the transition states have been considered and tested for their accuracy and ease of use. Despite initial difficulties the QTS2 method proved to be the most effective in determining the transition state of both the boat conformer in the Cope rearrangement and the endo and exo forms in the Diels-Alder reaction. It gave a good prediction for the geometries and energies of the transition states and allowed comparison between the reactants and products of the reactions. Further examples of Diels-Alder reactions could be looked at to determine the stereo and regio-selective implications of the mechanism and further prove the effectiveness of calculating activation energies by this method as compared to experimentally determined values. Also calculations from different basis sets could be run to determine the accuracy of the different levels of theory and to improve the calculated geometries and energies of the transition states studied in this experiment.