Rep:Mod:PhyComp101292
Cope Rearrangement
Introduction
[3,3]-sigmatropic shift rearrangement has been the subject of numerous experimental and computational studies. For many years, the actual mechanism was debated; the reaction can proceed in a concerted, dissociative or stepwise manner. Today, evidences suggest that the reaction proceeds in a concerted manner via a “chair” or a “boat” transition state where the “chair” transition state lies few kJmol-1 lower in energy. In this exercise, the B3LYP/6-31G model will be employed to optimise the structure of both transition states. The activation energy of both pathways will be computed to determine the preferred mechanism of the Cope rearrangement and see if the result agrees well with the literature. The reaction scheme is summarised in the scheme below
Aim
By rotating the central C-C sigma bond, different conformers of 1,5-hexadiene can be generated. We start off by optimising the conformation with the two substituents anti-periplanar with respect to each other. The optimisation process was done using the HF/3-21 G basis-set and then the structure will be re-optimised using the more accurate B3LYP/6-31G* basis-set. Other conformations with the substituents occupying different positions will also be studied.
Optimisation via Hartree/3-21 G)
Optimisation of 1,5-hexadiene (Anti 1)
The 3D Structure can be seen here
The log file for this calculation can be found here File:KlOPTIMISATION OF HEXADIENE (ANTI 1).LOG
The settings and results are shown below
The most important information is the gradient since the derivative of energy is force. If the gradient is 0 then there is no net force acting on the molecule and the molecule is at a stable minimum point. The value of the gradient in this case is very close to 0 suggesting that the minimum point was identified and the optimisation was successful.
Item Value Threshold Converged?
Maximum Force 0.000055 0.000450 YES
RMS Force 0.000010 0.000300 YES
Maximum Displacement 0.000379 0.001800 YES
RMS Displacement 0.000158 0.001200 YES
Predicted change in Energy=-1.526246D-08
Optimization completed.
-- Stationary point found.
From the table above, the forces were converged and this reinforces the fact that the optimisation was successful.
Optimisation of 1,5-hexadiene (Anti 2)
The 3D Structure can be seen here
The log file for this calculation can be found here File:KlOPTIMISATION OF HEXADIENE (ANTI 2).LOG
The settings and results are shown below
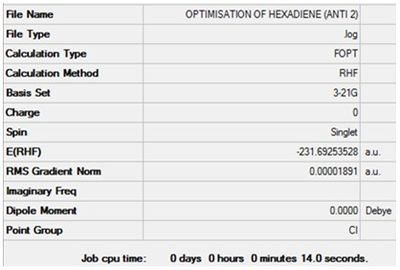
The value of the gradient is very close to 0 suggesting that the optimisation was successful.
Item Value Threshold Converged?
Maximum Force 0.000060 0.000450 YES
RMS Force 0.000010 0.000300 YES
Maximum Displacement 0.000516 0.001800 YES
RMS Displacement 0.000171 0.001200 YES
Predicted change in Energy=-2.037087D-08
Optimization completed.
-- Stationary point found.
From the table above, the forces were converged and this reinforces the fact that the optimisation was successful.
Optimisation of 1,5-hexadiene (Gauche 3)
The 3D Structure can be seen here
The log file for this calculation can be found here File:KlOPTIMISATION OF HEXADIENE (Gauch 3).LOG
The settings and results are shown below
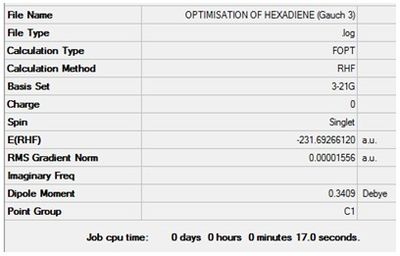
The value of the gradient is very close to 0 suggesting that the optimisation was successful.
Item Value Threshold Converged?
Maximum Force 0.000044 0.000450 YES
RMS Force 0.000009 0.000300 YES
Maximum Displacement 0.001476 0.001800 YES
RMS Displacement 0.000493 0.001200 YES
Predicted change in Energy=-3.610722D-08
Optimization completed.
-- Stationary point found.
From the table above, the forces were converged and this reinforces the fact that the optimisation was successful.
Optimisation of 1,5-hexadiene (Gauche 4)
The 3D Structure can be seen here
The log file for this calculation can be found here File:KlOPTIMISATION OF HEXADIENE (GAUCH 4).LOG
The settings and results are shown below
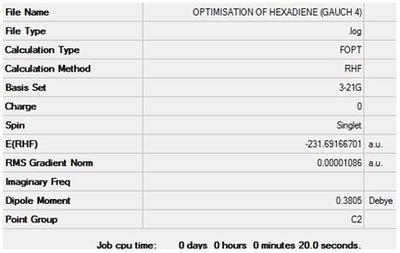
The value of the gradient is very close to 0 suggesting that the optimisation was successful.
Item Value Threshold Converged?
Maximum Force 0.000018 0.000450 YES
RMS Force 0.000006 0.000300 YES
Maximum Displacement 0.000800 0.001800 YES
RMS Displacement 0.000331 0.001200 YES
Predicted change in Energy=-1.009941D-08
Optimization completed.
-- Stationary point found.
From the table above, the forces were converged and this reinforces the fact that the optimisation was successful.
Optimisation + Frequency Analysis via B3LYP/6-31G*)
B3LYP/6-31G* is a much better basis set and provides more accurate results despite longer calculation time compared to HF/3-21G. Frequency analysis is carried out to confirm that the optimised structure is at the minimum point of the potential surface. Although the gradient in the optimisation calculation is very close to 0,it just means the molecule is at a turning point, it can either be a maximum or a minimum. We need to consider the 2nd derivative of the potential surface to confirm that the turning point is a minimum. The 2nd derivative of potential surface is effectively the frequency, hence if the frequency is negative then the turning point is a maximum (transition state) and if it is positive then it is a minimum point. Frequency analysis also allows us to determine whether the frequencies are real ie within the range of ±15cm-1 as well as providing Thermochemistry and IR spectrocopic data.
Optimisation + Frequency Analysis of 1,5-hexadiene (Anti 1)
The log files can be found here: File:Kl 6-31G OPTIMISATION OF HEXADIENE (ANTI 1).LOG and File:KlFrequency analysis of hexadiene (ANTI 1).LOG
The 3D Structure can be seen here
The settings and results are shown below
).jpg)
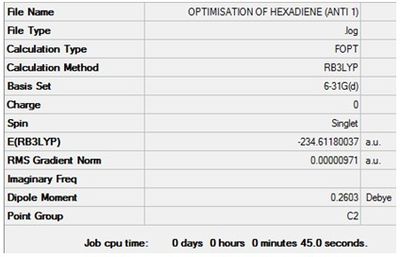
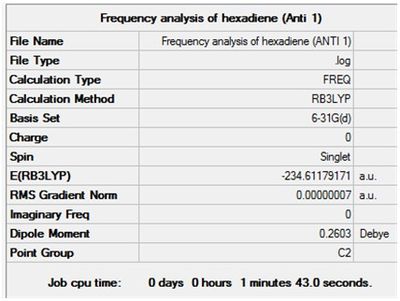
The value of the gradient is very close to 0 suggesting that the optimisation was successful.
Item Value Threshold Converged?
Maximum Force 0.000012 0.000450 YES
RMS Force 0.000005 0.000300 YES
Maximum Displacement 0.000160 0.001800 YES
RMS Displacement 0.000067 0.001200 YES
Predicted change in Energy=-9.063092D-09
Optimization completed.
-- Stationary point found.
From the table above, the forces were converged and this reinforces the fact that the optimisation was successful.
There are no imaginary frequencies
Low frequencies --- -6.5500 -3.2145 -0.0007 0.0006 0.0008 3.3524 Low frequencies --- 74.1783 98.0287 113.7145
Sum of electronic and zero-point Energies= -234.469305 Sum of electronic and thermal Energies= -234.461974 Sum of electronic and thermal Enthalpies= -234.461030 Sum of electronic and thermal Free Energies= -234.500220
Optimisation + Frequency Analysis of 1,5-hexadiene (Anti 2)
The log files can be found here: File:Kl 6-31GOPTIMISATION OF HEXADIENE (ANTI 2).LOG and File:KlFrequency analysis of hexadiene (ANTI 2).LOG
The 3D Structure can be seen here
The settings and results are shown below
).jpg)
The value of the gradient is very close to 0 suggesting that the optimisation was successful.
Item Value Threshold Converged?
Maximum Force 0.000015 0.000450 YES
RMS Force 0.000006 0.000300 YES
Maximum Displacement 0.000219 0.001800 YES
RMS Displacement 0.000079 0.001200 YES
Predicted change in Energy=-1.588865D-08
Optimization completed.
-- Stationary point found.
From the table above, the forces were converged and this reinforces the fact that the optimisation was successful.
There are no imaginary frequencies
Low frequencies --- -7.6846 -2.7154 -0.0008 0.0003 0.0006 1.6605 Low frequencies --- 73.5514 80.5643 121.0103
Sum of electronic and zero-point Energies= -234.469219 Sum of electronic and thermal Energies= -234.461869 Sum of electronic and thermal Enthalpies= -234.460925 Sum of electronic and thermal Free Energies= -234.500808
Optimisation + Frequency Analysis of 1,5-hexadiene (Gauche 3)
The log files can be found here: File:Kl 6-31GOPTIMISATION OF HEXADIENE (GAUCH 3).LOG and File:KlFrequency analysis of hexadiene (GAUCH 3).LOG
The 3D Structure can be seen here
The settings and results are shown below
).jpg)
The value of the gradient is very close to 0 suggesting that the optimisation was successful.
Item Value Threshold Converged?
Maximum Force 0.000006 0.000450 YES
RMS Force 0.000002 0.000300 YES
Maximum Displacement 0.000530 0.001800 YES
RMS Displacement 0.000133 0.001200 YES
Predicted change in Energy=-1.487598D-09
Optimization completed.
-- Stationary point found.
From the table above, the forces were converged and this reinforces the fact that the optimisation was successful.
There are no imaginary frequencies
Low frequencies --- -0.0006 -0.0004 0.0003 2.1011 3.5412 6.4601 Low frequencies --- 73.5488 100.9878 123.9092
Sum of electronic and zero-point Energies= -234.468719 Sum of electronic and thermal Energies= -234.461477 Sum of electronic and thermal Enthalpies= -234.460533 Sum of electronic and thermal Free Energies= -234.500173
Optimisation + Frequency Analysis of 1,5-hexadiene (Gauche 4)
The log files can be found here: File:Kl 6-31GOPTIMISATION OF HEXADIENE (GAUCH 4).LOG and File:KlFrequency analysis of hexadiene (GAUCH 4).LOG
The 3D Structure can be seen here
The settings and results are shown below
).jpg)
The value of the gradient is very close to 0 suggesting that the optimisation was successful.
Item Value Threshold Converged?
Maximum Force 0.000010 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000701 0.001800 YES
RMS Displacement 0.000231 0.001200 YES
Predicted change in Energy=-5.277948D-09
Optimization completed.
-- Stationary point found.
From the table above, the forces were converged and this reinforces the fact that the optimisation was successful.
There are no imaginary frequencies
Low frequencies --- -2.8305 -0.0010 -0.0006 -0.0003 3.9521 5.0823 Low frequencies --- 65.6750 101.7133 108.1475
Sum of electronic and zero-point Energies= -234.468244 Sum of electronic and thermal Energies= -234.460957 Sum of electronic and thermal Enthalpies= -234.460013 Sum of electronic and thermal Free Energies= -234.499226
Summary
| Structure | Energy 3-21G (Hartree) | Relative Energy to Gauche 3 (kCal/mol) | Energy 6-31G* (Hartree) | Relative Energy to Gauche 3 (kCal/mol) | Sum of electronic and zero-point Energies (Hartree) | Sum of electronic and thermal Energies (Hartree) | Sum of electronic and thermal Enthalpies (Hartree) | Sum of electronic and thermal Free Energies (Hartree) | Point Group |
|---|---|---|---|---|---|---|---|---|---|
| -231.69260235 | 0.04 | -234.61180037 | 0.30 | -234.469305 | -234.461974 | -234.461030 | -234.500220 | C2 | |
| -231.69253528 | 0.08 | -234.61170280 | 0.23 | -234.469219 | -234.461869 | -234.460925 | -234.500808 | Ci | |
| -231.69266120 | 0.00 | -234.61132934 | 0.00 | -234.468719 | -234.461477 | -234.460533 | -234.500173 | C1 | |
| -231.69166701 | 0.62 | -234.61070764 | 0.39 | -234.468244 | -234.460957 | -234.460013 | -234.499226 | C2 |
Based on the information above, it can be seen that both HF/3-21G and B3LYP/6-31G* basis-set leads to the same structure for a particular conformer.
The conformation with the lowest energy is Gauche 3, hence this is the most stable conformer of 1,5-hexadiene.
The relative stabilities of the gauche and app conformations is governed by three main factors; APP orbital interactions, steric repulsions and The Van Der Wall's Forces. For vinyl, although there are no electronegative atoms, πC-C is a higher energy donor than σC-H meaning that the πC-C interacts better with the π*C-C app so APP arrangement of the two vinyl group is favourable. Vinyl group is relatively big so steric strain is reduced when they are APP with respect to each other. Therefore both factor 1 and 2 favours the APP arrangement.
In the HF/3-21G basis set, the gauche conformations were surprisingly more stable than the APP ones. Based on the factors explained above, we would expect the APP conformations to have lower energies than the gauche ones. The results were not as expected probably because HF/3-21G basis set is too simple to account for electronic correlations and as a result, the stabilisation effect due to the πC-H-C→π* is overestimated and outweighing the steric clash between the two bulky substituents and hence favouring the gauche conformations.
In the B3LYP/6-31G* basis-set, the APP conformations are favoured as expected for the reason stated above, namely that the two substituents are as far apart as possible meaning that steric repulsion is minimised. The smooth overlap of the πC-C→π*C-C also favours this arrangement. Anti 1 is more stable than anti 2 as the two vinyl groups are staggered while the vinyl groups of Anti 2 are eclipsed. Staggered is favoured over eclipsed which is why anti 1 is lower than anti 2 in energy. This model is accurate enough to account for electronic correlation giving the expected result.
The Bond Lengths and Angles of Anti 2 are summarised below
| Bond | HF/3-21G (A) | B3LYP/6-31G* (A) | Angle | HF/3-21G | B3LYP/6-31G* |
|---|---|---|---|---|---|
| C1-C2, C5-C6 | 1.32 | 1.33 | C1-C2-C3, C4-C5-C6 | 124.8 | 125.3 |
| C2-C3, C4-C5 | 1.51 | 1.50 | C2-C3-C4, C3-C4-C5 | 111.3 | 112.7 |
| C3-C4 | 1.55 | 1.55 | NA | NA | NA |
The bond lengths and angles are closer to experimental results in the B3LYP/6-31G* basis-sets.
Optimisation of The Transition State (HF/3-21G)
There are various methods to optimise a transition state and each of these will be demonstrated.
Optimisation of The Allyl Fragment
This calculation is required to generate the structure of the transition state. The log file can be found here File:KlOPTIMISATION OF ALLYL FRAQMENT.LOG.
The setting and result are as follow:
Item Value Threshold Converged?
Maximum Force 0.000153 0.000450 YES
RMS Force 0.000077 0.000300 YES
Maximum Displacement 0.001150 0.001800 YES
RMS Displacement 0.000603 0.001200 YES
Predicted change in Energy=-4.449593D-07
Optimization completed.
-- Stationary point found.
Based on the information above, the convergence was successful.
Optimisation of The Transition State by Computing the Force Constant
Two lots of the optimised fragment was copied to a new Gaussview window. Both terminal ends of the two fragments was set to 2.2 A apart from each other. The optimisation was carried out and the log file can be found here File:Kl GUESSED TS CHAIR.LOG
The settings and results was as follow
The value of the gradient is very close to 0 suggesting that the optimisation was successful.
Item Value Threshold Converged?
Maximum Force 0.000037 0.000450 YES
RMS Force 0.000012 0.000300 YES
Maximum Displacement 0.001118 0.001800 YES
RMS Displacement 0.000234 0.001200 YES
Predicted change in Energy=-8.125308D-08
Optimization completed.
-- Stationary point found.
From the table above, the forces were converged and this reinforces the fact that the optimisation was successful.
The most important imaginary frequency (-818 cm-1) is present and this suggests that the transition state is reached.
Low frequencies --- -818.0169 -3.4046 -0.0009 -0.0007 -0.0004 2.5837 Low frequencies --- 3.2377 209.5117 395.8642
Sum of electronic and zero-point Energies= -231.466701 Sum of electronic and thermal Energies= -231.461341 Sum of electronic and thermal Enthalpies= -231.460397 Sum of electronic and thermal Free Energies= -231.495207
Optimisation of The Transition State Via Redundant coordinate editor
The log file for this calculation can be found here File:KlCHAIR TS (FROZEN COORDINATE METHOD PART D).LOG
The settings and results was as follow
The value of the gradient is very close to 0 suggesting that the optimisation was successful.
Item Value Threshold Converged?
Maximum Force 0.000074 0.000450 YES
RMS Force 0.000022 0.000300 YES
Maximum Displacement 0.001548 0.001800 YES
RMS Displacement 0.000392 0.001200 YES
Predicted change in Energy=-1.931135D-07
Optimization completed.
-- Stationary point found.
Based on the information above, the minimisation was successful.
The most important imaginary frequency (-818 cm-1) is present and this suggests that the transition state is reached.
Low frequencies --- -817.8731 -0.0005 -0.0001 0.0003 0.5560 5.5385 Low frequencies --- 8.2496 209.6239 395.9590
Sum of electronic and zero-point Energies= -231.466704 Sum of electronic and thermal Energies= -231.461345 Sum of electronic and thermal Enthalpies= -231.460401 Sum of electronic and thermal Free Energies= -231.495211
Optimisation of The Transition State by QST2
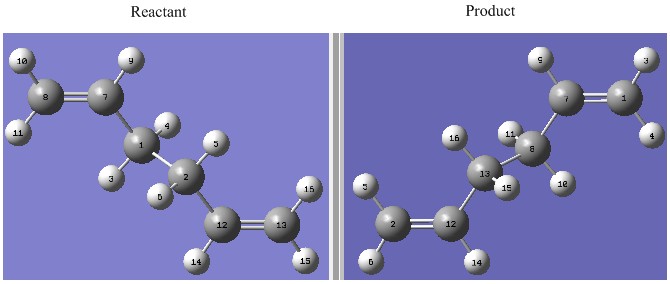
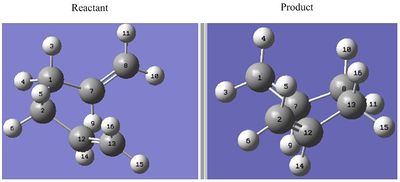
Unlike the first two methods where we actually build the transition state, this method predicts the transition state by interpolating between the structure of the reactant and product. Therefore the atom label between the reactant and product must corresponds to each other just like the case shown below.
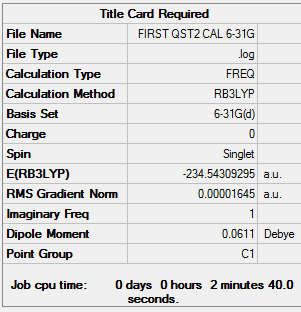
The above was optimised using QST2 setting and the log file for this calculation can be found here File:FIRST QST2 CAL.LOG
The optimisation was not successful, the structure is similar to the chair transition structure but more dissociated. During the imterpolation between the two structures, the top allyl fragment was simply translated and the possibility of a rotation around the central bonds was not considered at all. If we start with these structures of the product and reactant, it is clear that the boat transition state will never be located. Therefore the structures of the product and reactant must resemble the boat transtion state so the structures were changed as follow
The log file for this calculation can be found here. File:KlFIRST QST2 CAL.LOG
The settings and results were as follow
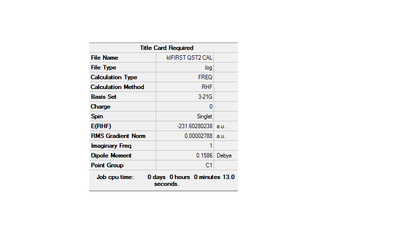
Item Value Threshold Converged?
Maximum Force 0.000067 0.000450 YES
RMS Force 0.000015 0.000300 YES
Maximum Displacement 0.001391 0.001800 YES
RMS Displacement 0.000353 0.001200 YES
Predicted change in Energy=-1.075013D-07
Optimization completed.
-- Stationary point found.
Base on the above information the convergence is now successful.
The most important imaginary frequency (-840 cm-1) is present and this suggests that the transition state is reached.
Low frequencies --- -840.1921 -1.6525 0.0006 0.0008 0.0008 3.0246 Low frequencies --- 5.5986 155.3989 382.1404
Sum of electronic and zero-point Energies= -231.450928 Sum of electronic and thermal Energies= -231.445300 Sum of electronic and thermal Enthalpies= -231.444356 Sum of electronic and thermal Free Energies= -231.479772
From this calculation, we can conclude that the the QST2 method will only locate the transtion state only if the structure of the reactant and product is reasonably close to the real structure of the transition state. Therefore this is a poor method if we know very little information about the real structure of the transition state. If we have good knowledge about the transitions state then this would be the most efficient method.
Intrinsic Reaction Coordinate
IRC is important as it tells us which conformers of 1,5-hexadiene connects, it allow us to follow the minimum energy path from a transition structure down to its local minimum on a potential energy surface. Without this technique it is very difficult to predict which conformer the reaction paths from the transitions structures will lead to. IRC will be demonstrated on the HF/3-21G optimised chair conformation to locate its transition state.
| Energy | Dihedral Angle | Structure | Point Group | IRC plot | Log file | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Initial IRC | -231.69157923 | 67.2 |
|
C2 |  |
File:Kl IRC.LOG | ||||
| Further IRC | -231.69166702 | 64.2 |
|
C2 |  |
File:Kl IRC2.LOG |
In the first run, the number of points along the IRC was set to 50. From the structure, it is clear that the transition state is not reached as its energy nor structure does not corresponds to any of the conformers listed in Appendix 1 despite the fact that the IRC plot tends towards a stationary point near the end of the calculation. Hence the last point of the IRC path was optimised using HF/3-21 G to proceed further. From the graph of this optimisation process, the energy still decreases reinforcing the fact that the minimum point was not reached initially. The result suggests that the optimisation was successful since it is converged.
Item Value Threshold Converged? Maximum Force 0.000010 0.000450 YES RMS Force 0.000003 0.000300 YES Maximum Displacement 0.000298 0.001800 YES RMS Displacement 0.000091 0.001200 YES Predicted change in Energy=-2.405357D-09 Optimization completed. -- Stationary point found.
The energy of the optimised structure matches exactly with the one of Gauche 2 in Appendix 1.Therefore the IRC method suggests that Gauche 2 is the conformer of 1,5-hexadiene that leads to the chair transition state structure in the Cope Rearrangement of 1,5-hexadiene.
Optimisation of The Transition State by B3LYP/6-31G*
Optimisation of The Transition State by Computing the Force Constant
The optimisation was carried out and the log file can be found here File:KlGUESSED TS CHAIR.LOG
The settings and results was as follow
The value of the gradient is very close to 0 suggesting that the optimisation was successful.
Item Value Threshold Converged?
Maximum Force 0.000023 0.000450 YES
RMS Force 0.000006 0.000300 YES
Maximum Displacement 0.000085 0.001800 YES
RMS Displacement 0.000027 0.001200 YES
Predicted change in Energy=-4.040758D-09
Optimization completed.
-- Stationary point found.
From the table above, the forces were converged and this reinforces the fact that the optimisation was successful.
The most important imaginary frequency (-566 cm-1) is present and this suggests that the transition state is reached.
Low frequencies --- -565.6435 -0.0007 -0.0006 0.0003 22.0004 27.2717 Low frequencies --- 39.5182 194.6021 267.8645
Sum of electronic and zero-point Energies= -234.414929 Sum of electronic and thermal Energies= -234.409008 Sum of electronic and thermal Enthalpies= -234.408064 Sum of electronic and thermal Free Energies= -234.443159
Optimisation of The Transition State Via Redundant coordinate editor
The log file for this calculation can be found here File:Kl6-31GdCHAIR TS (FROZEN COORDINATE METHOD).LOG
The settings and results was as follow
The value of the gradient is very close to 0 suggesting that the optimisation was successful.
Item Value Threshold Converged?
Maximum Force 0.000029 0.000450 YES
RMS Force 0.000010 0.000300 YES
Maximum Displacement 0.001111 0.001800 YES
RMS Displacement 0.000419 0.001200 YES
Predicted change in Energy=-1.749175D-07
Optimization completed.
-- Stationary point found.
Based on the information above, the minimisation was successful.
The most important imaginary frequency (-565 cm-1) is present and this suggests that the transition state is reached.
Low frequencies --- -565.3598 -0.0008 0.0003 0.0006 21.5705 27.1004 Low frequencies --- 39.2434 194.4948 268.2299
Sum of electronic and zero-point Energies= -234.414923 Sum of electronic and thermal Energies= -234.409004 Sum of electronic and thermal Enthalpies= -234.408059 Sum of electronic and thermal Free Energies= -234.443153
Optimisation of The Transition State by QST2
The atom label between the reactant and product corresponds to each other.
The above was optimised using B3LYP3/6-31G* QST2 setting and the log file for this calculation can be found here File:FIRST QST2 CAL 6-31G.LOG
The settings and results were as follow
Item Value Threshold Converged? Maximum Force 0.000051 0.000450 YES RMS Force 0.000012 0.000300 YES Maximum Displacement 0.000824 0.001800 YES RMS Displacement 0.000217 0.001200 YES Predicted change in Energy=-4.980745D-08 Optimization completed. -- Stationary point found.
Base on the above information the convergence is now successful.
The most important imaginary frequency (-530 cm-1) is present and this suggests that the transition state is reached.
Low frequencies --- -530.0304 -9.4662 -0.0006 -0.0006 -0.0005 15.4582 Low frequencies --- 17.6698 135.5764 261.5656
Sum of electronic and zero-point Energies= -234.402344 Sum of electronic and thermal Energies= -234.396008 Sum of electronic and thermal Enthalpies= -234.395064 Sum of electronic and thermal Free Energies= -234.431755
Comparison of bond lengths between HF/3-21G and B3LYP/6-31G*
Both the force constant and the freezing coordinate method results in identical bond lengths
| Bond | Bond Length HF/3-21G (A) | Bond Length B3LYP/6-31G* (A) |
|---|---|---|
| C10-C15, C2-C8 | 1.39 | 1.39 |
| C10-C16, C2-C7 | 1.39 | 1.39 |
| C8-C15, C7-C16 | 1.55 | 2.02 |
The Bond Lengths of QST2 method is summarised below
| Bond | Bond Length HF/3-21G (A) | Bond Length B3LYP/6-31G* (A) |
|---|---|---|
| C10-C15, C2-C8 | 1.38 | 1.39 |
| C10-C16, C2-C7 | 1.38 | 1.39 |
| C8-C15, C7-C16 | 2.14 | 2.21 |
Diels Alder Reaction
Optimisation of 1,3-Cis Butadiene (Empirical/AM1)
The log file for this calculation can be found here File:KlOPT BUTADIENE (SEMI EMPIRICAL).LOG
The settings and results were as follow
Item Value Threshold Converged? Maximum Force 0.000030 0.000450 YES RMS Force 0.000011 0.000300 YES Maximum Displacement 0.000407 0.001800 YES RMS Displacement 0.000162 0.001200 YES Predicted change in Energy=-9.691189D-09 Optimization completed. -- Stationary point found.
Base on the above the optimisation was successful
| MO | HOMO | LUMO |
|---|---|---|
| Structure |  |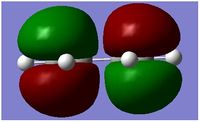
|
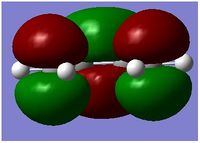
| Energy Level | 11 | 12 |
| Energy | -0.34381 | 0.01707 |
| Symmetry With Respect to Plane | Assymmetric | Symmetric |
Optimisation of 1,3-Cis Butadiene (B3LYP/6-31G*)
The log file for this calculation can be found here File:KlOPT BUTADIENE (6-31G).LOG
The settings and results were as follow
File:KlOPT BUTADIENE (6-31G).LOG
Item Value Threshold Converged?
Item Value Threshold Converged?
Maximum Force 0.000090 0.000450 YES
RMS Force 0.000035 0.000300 YES
Maximum Displacement 0.000427 0.001800 YES
RMS Displacement 0.000156 0.001200 YES
Predicted change in Energy=-5.870266D-08
Optimization completed.
-- Stationary point found.
Base on the above the optimisation was successful
| MO | HOMO | LUMO |
|---|---|---|
| Structure | |
|
| Energy Level | 15 | 16 |
| Energy | -0.32141 | 0.12345 |
| Symmetry With Respect to Plane | Assymmetric | Symmetric |
Optimisation of Transition State of The DA Reaction Between Ethene and Butadiene
The distant between the two terminal carbon atoms was guessed to be 2A. The above was initially optimised using Semi-empirical/Am1 and then re-optimised with B3LYP/6-31G*. The HOMO and LUMO was plotted to identify the symmetry and the orbital overlapping of the frontier orbitals during the transition state.
The log files can be found here File:KlSEMIempirical.LOG, File:Kl 6-31G DA part 2.LOG
The results are summarised in the table below
| Semi-empirical/AM1 | B3LYP/6-31G* | |
|---|---|---|
| Length Between Terminal ends | 2.12 | 2.27 |
| Energy (a.u) | 0.11165468 | -234.54389654 |
| Point Group | C1 | C1 |
| Imaginary Frequency | -956 | -525 |
| MO | HOMO(AM1) | LUMO(AM1) | HOMO(6-31G*) | LUMO(6-31G*) |
|---|---|---|---|---|
| Structure |  |
 |
|
|
| Energy Level | 17 | 18 | 23 | 24 |
| Energy | -0.32393 | 0.02315 | -0.21895 | -0.00861 |
| Symmetry With Respect to Plane | Assymmetric | Symmetric | Assymmetric | Symmetric |
From the above table, it is clear that the partially formed sigma bonds are shorter than 2x VDW radius of the sp2 carbon atoms (3.4 A) but longer than the covalent bond between the sp2 carbon atoms. This means that the formation of the new sigma bonds between Cis 1,3-Butadiene and ethene was successful suggesting that the predicted transition state is correct.
The HOMO of the TS is anti-symmetric with respect to the plane, this is understandable as this orbital is formed from the HOMO of butadiene and the LUMO of ethylene which are both anti-symmetric. Additionally, there are notable amount of electron density about where the new sigma bonds formed. Therefore, this reaction is allowed by the Woodward-Hoffmann rule.
The animation below shows how the new bonds are formed
This is the vibrational mode of the imaginary frequency based on the Empirical/AM1 calculation. The terminal carbon atoms of the 1,3-Cis Butadiene and ethylene approaches each other in a concerted fashion so the bonds form synchronously where the atoms of both reactants are stretching vigously.
Compared to the first "Real" bending motion of the vibrational mode at 147 cm-1, the frequency corresponding to the TS vibrational mode is -956 cm-1 which is a lot higher in magnitude. This vibrational mode involves the stretching of both reactants which involves a lot more energy and hence a higher frequency than the simple bending motion in the first "Real" vibrational mode.
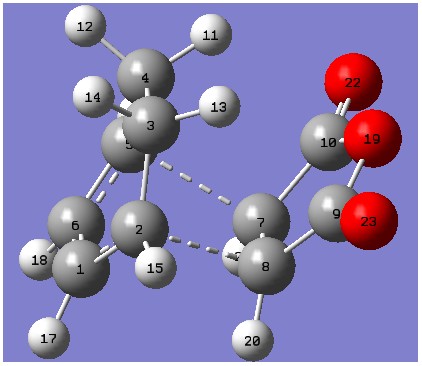
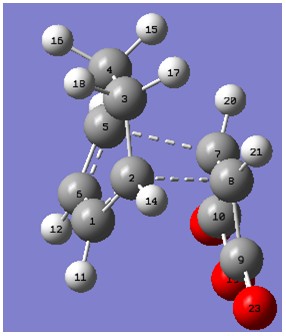
Diels Alder Cycloaddition of Maleic Anhydride and Cyclohexadiene
Through this reaction, there are two possible transition states and this determines whether we get the exo or the endo product. Both the endo and exo transition state is optimised by Empirical/AM1 followed by B3LYP/6-31G*.
The log files can be found here: File:KL PART 3 DA exo (AM1).LOG, File:Kl Part 3 DA Endo (AM1).LOG, File:KL PART 3 DA Exo 6-31G.LOG, File:Kl Part 3 DA Endo (6-31G).LOG
The results are summarised below
| Semi-empirical/AM1 | B3LYP/6-31G* | |
|---|---|---|
| Structure | _.jpg) |
|
| Energy (a.u) | -0.05041966 | -612.67931094 |
| Bond Length (C1-C2)/(C5-C6) | 1.39 | 1.39 |
| Bond Length (C1-C6) | 1.40 | 1.40 |
| Bond Length (C2-C8)/(C5-C7) | 2.17 | 2.29 |
| Bond Length (C7-C8) | 1.41 | 1.39 |
| Bond Length (C3-C9)/(C4-C10) | 2.94 | 3.03 |
| Point Group | C1 | C1 |
| Imaginary Frequency | -812 | -449 |
| MO | HOMO(AM1) | LUMO(AM1) | HOMO(6-31G*) | LUMO(6-31G*) |
|---|---|---|---|---|
| Structure |  |
 |
|
|
| Energy Level | 34 | 35 | 47 | 48 |
| Energy | -0.34273 | -0.04046 | -0.24216 | -0.07840 |
| Symmetry With Respect to Plane | Asymmetric | Asymmetric | Asymmetric | Asymmetric |
| Semi-empirical/AM1 | B3LYP/6-31G* | |
|---|---|---|
| Structure | .jpg) |
|
| Energy (a.u) | -0.05150480 | -612.68339668 |
| Bond Length (C1-C2)/(C5-C6) | 1.39 | 1.39 |
| Bond Length (C1-C6) | 1.40 | 1.40 |
| Bond Length (C2-C8)/(C5-C7) | 2.16 | 2.27 |
| Bond Length (C7-C8) | 1.41 | 1.39 |
| Bond Length (C3-C9)/(C4-C10) | 3.90 | 3.94 |
| Point Group | C1 | C1 |
| Imaginary Frequency | -806 | -447 |
The transition state was successfully optimised as the new sigma bond length between C2 and C8 and C5 and C7 are identical in both the Empirical/AM1 ( 2.16 A) and B3LYP/6-31G* (2.27 A) confirming that the new bonds are formed in a concerted manner. Furthermore, the presence of the imaginary frequency suggests that a energy maxima is achieved.
The endo and the exo structure differs by the orientation of the dienophile with respect to the diene. In the endo structure, the aldehyde is in the opposite phase with respect to the -CH2-Ch2- bridge whereas the aldehyde is in the same phase with the -CH2-Ch2- in the exo structure. From this point, we can see that the exo structure is sterically more hindered as there is a steric clash between the bridge and the aldehyde. This was illustrated in the B3LYP/6-31G* calculation where the distant between C3-C9/C4-C10 was 3.03 A in the exo structure and 3.94 A in the endo structure. Therefore the distant between the two groups are further apart in the endo structure making it energetically favoured due to less repulsion and hence lower in energy compared to the exo structure.
| MO | HOMO(AM1) | LUMO(AM1) | HOMO(6-31G*) | LUMO(6-31G*) |
|---|---|---|---|---|
| Structure |  |
 |
|
|
| Energy Level | 34 | 35 | 47 | 48 |
| Energy | -0.34273 | -0.04046 | -0.24231 | -0.06773 |
| Symmetry With Respect to Plane | Asymmetric | Asymmetric | Asymmetric | Asymmetric |
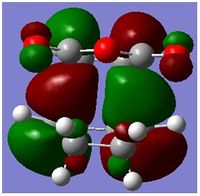
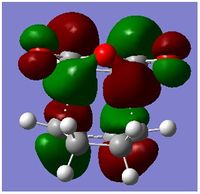
From the above, all the MOs of the transition state were identified as anti-symmetric with respect to the plane. Based on the symmetry rules from the Woodward-Hoffmann, it is forbidden. The energy gap of the HOMO of the cyclohexadiene and LUMO of Maleic aldehyde was smaller than the energy gap of the HOMO of Maleic Aldehyde and the LUMO of cyclohexadiene . Since this reaction is kinetically control, the one with the smallest energy gap is favoured, ie the main orbital interactions leading the reaction is the overlap of the HOMO of cyclohexadiene and the LUMO of Maleic Aldehyde. Both of these orbital are anti-symmetric with respect to the plane which is why the MO transition state is assymetric with respect to the plane.
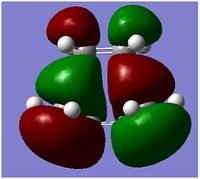
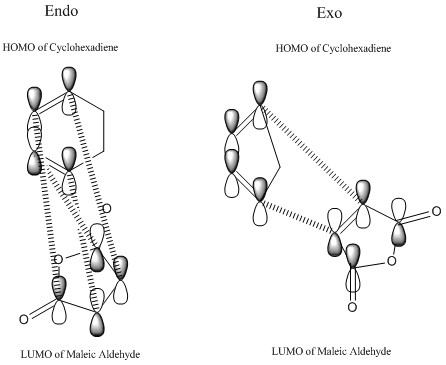
Secondary Orbital Overlap explains why the energy of the endo transition state is lower than the energy exo transition state. Secondary Orbital Overlap is defined by the bonding interaction of frontier orbitals between the atoms that are not involved in the sigma bond formation.
The following can be explained by the diagram below
From the above, we can see that there are more favorable orbital overlaps in the endo structure than in the case of the exo structure. In the endo structure, there are secondary orbital overlap which is absent in the exo structure. These interactions stabilises the molecule, and this is the primary reason why the endo structure is favoured over the exo structure as well as the steric factor mentioned above.
The vibrational mode of the transition state was studied to determine whether the reaction proceeds via synchronously or asynchronously.
The vibrational mode shown above is very similar to the one of the Diels Alder reaction between ethene and butadiene, ie both reactants stretch towards each other in a concerted motion. Therefore the bond formation is synchronous.
Further Discussion
All the calculations was repeated with B3LYP/6-31G* as Empirical/AM1 fails to account for the effect of differential diatomic overlap. In the advanced B3LYP/6-31G*, the polarisation effect is accounted giving results that are more comparable to real experimental results.
The scope of this investigation was only limited to Normal Electron Demand of Diels Alder reaction, the Inverse Electron Demand of Diels Alder reaction was not covered. In this type of reaction, the energy of the LUMO of the diene lies higher in energy than the HOMO of the dienophile meaning that the flow of electrons will be reversed and hence the name Inverse Electron Demand. This type of reaction can be achieved when the diene is made electron deficient and the dienophile is made electron rich. This is an interesting reaction as it requires hetero atoms and forms hetero-aromatic species which can be useful in the pharmaceutical industry. Therefore, it will be beneficial to study this type of reaction.
Another important factor which was neglected throughout this computational exercise was the regio-selectivity. There was no issue with regio-seletivity in the examples that were covered but in reality changing the electronegativity of the substituents can alter the regioselectivity and this could be investigated with Frontier Molecular Orbital analysis.
There are many other factors that could have been investigated such as the temperature and solvent employed during the reaction. Gaussview has the ability to change these settings and this allows us to investigate whether there would be any changes in energy and selectivity.