The Free Energy and Thermal Expansion of MgO

Introduction

Thermal expansion of the material is one of important physical property as the behaviour of material at different temperature is crucial property for designing large structures, engineering applications and mechanical applications. In this experiment the thermal expansion of MgO was studied using the General Utility Lattice Program (GULP) at Linux operating system. The thermal expansion of MgO can be studied by calculating vibration states and the free energy of the crystal at different temperatures. The thermal expansion coefficient was calculated using two different models, Quasi-Harmonic and Molecular dynamic model and compared to see the differences of using different models. The equation below shows the thermal expansion coefficient calculated by the initial volume ( Volume at 0 K) and the the change of volume with respect to temperature. ^[1]

α_{V} = \frac{1}{V_{0}} {(\frac{\partial V}{\partial T})}_{p}

The Bloch function can be used to describe the MgO lattice as it can be described as periodically repeating environment. Commonly, the Bloch function is used to describe electrons in the crystal, but it can be applied to describe the vibration of the lattice. And in this experiment the Bloch function is used to describe the vibration in a system.

The Quasi-Harmonic approximation was used to compute vibrational energy levels of MgO. As the harmonic approximation is not suitable to calculate thermal expansion because the equilibrium position does not change where for the thermal expansion the equilibrium position changes. And therefore Quasi-Harmonic approximation was used for the calculation as it is a phonon-based model used to describe volume-dependent thermal effect such as thermal expansion. Quasi-Harmonic approximation assumes that the harmonic approximation holds for every value of the lattice constant and is better approximation for the thermal expansion. The free energy for Quasi harmonic approximation is calculated by adding all the vibrational modes of the crystal lattice. And thermal expansion of the crystal was monitored by looking the volume which minimise the free energy at different temperature. Below equation shows the calculation of the free energy for the Quasi-Harmonic approximation.

F = E_{0} + \frac{1}{2} \sum_{k, j} ℏ ω_{j, k} + K_{B} T \sum_{k, j} l n [1 - e x p (- \frac{ℏ ω_{j, k}}{K_{B} T})]

The molecular dynamic model was also used to calculate the thermal expansion of MgO and compared with the Quasi-Harmonic approximation. Molecular dynamic model simulates the motions of the atoms in the real material by accelerating the atoms using the Newton’s Second law. Using molecular dynamic model the properties can be computed as time averages of atom’s behaviour. In this experiment the change in the volume was computed in different time steps.

Calculating the internal energy of an MgO crystal

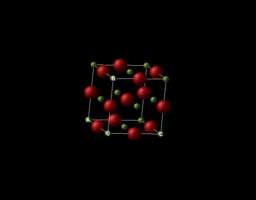
The MgO lattice is a face-centred cubic structure (FCC). The MgO lattice could be represented in two ways, conventional cell and primitive cell.

Conventional cell


Figure 1 : Conventional lattice of MgO

The conventional cell has equal lattice parameter and the internal angles are all equal to 90 degree.
$a_{c}$ , $b_{c}$ and $c_{c}$ where $a_{c} = b_{c} = c_{c}$
$α_{c} = β_{c} = γ_{c} =$ 90°
where $α_{c}$ is between $b_{c}$ and $c_{c}$ ,
$β_{c}$ is between $a_{c}$ and $c_{c}$ ,
$γ_{c}$ is between $a_{c}$ and $b_{c}$ ,

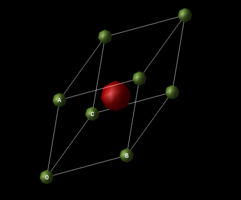
Primitive cell


Figure 2 :Primitive lattice of MgO

The primitive cell has also equal lattice parameter and the internal angles are all equal to 60 degree. $a_{p}$ , $b_{p}$ and $c_{p}$ where $a_{p} = b_{p} = c_{p}$
$α_{p} = β_{p} = γ_{p} =$ 60°
where $α_{p}$ is between $b_{p}$ and $c_{p}$ ,
$β_{p}$ is between $a_{p}$ and $c_{p}$ ,
$γ_{p}$ is between $a_{p}$ and $b_{p}$ ,

The output file for the calculation of internal energy of MgO

 Cell parameters (Angstroms/Degrees):

  a =   2.9783    alpha =  60.0000
  b =   2.9783    beta  =  60.0000
  c =   2.9783    gamma =  60.0000

The cell parameter from the output file shows that the internal energy of the crystal system was calculated in primitive cell as the angle is 60 degree. Using the lattice parameter of the primitive cell the lattice parameter for the conventional cell can be calculated. The diagonal of the conventional cell is equal to two times cell parameter of primitive cell.

$2 a_{p}^{2} = a_{c}^{2} + a_{c}^{2}$

$a_{c} = 4.21 t o 2 d . p .$

  Total lattice energy       =         -41.07531759 eV
--------------------------------------------------------------------------------
  Total lattice energy       =         -3963.1403 kJ/(mole unit cells)

The internal energy of MgO was calculated using Quasi-harmonic model. The internal energy shows the energy required to separate the two oppositely charged ions in the cell (Mg 2+ and O 2-) to an infinite distance apart. The internal energy of MgO was calculated with assumption of the crystal lattice is perfect and it has no defects.

Lattice Vibrations - Computing the Phonons

Phonon Dispersion
Phonon dispersion shows the relation of the energies at different symmetry points and the number of vibration states. From the figure 3, the 6 vibration states can be found.


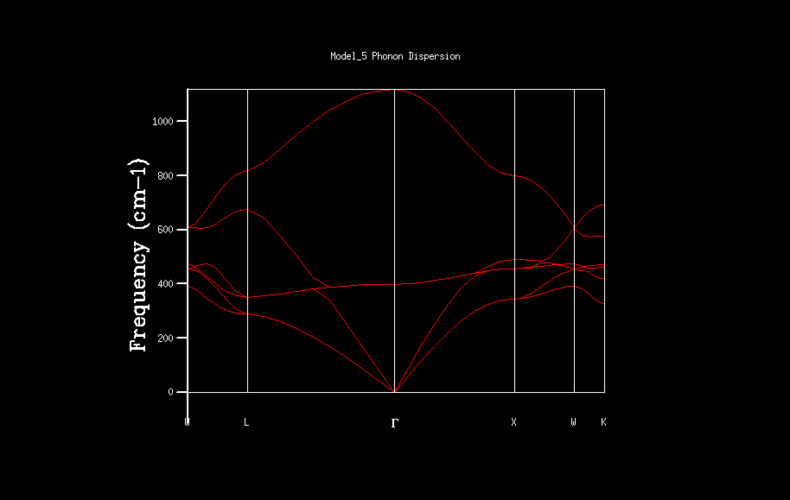Figure 3: Phonon dispersion for 1x1x1 shrinking factor

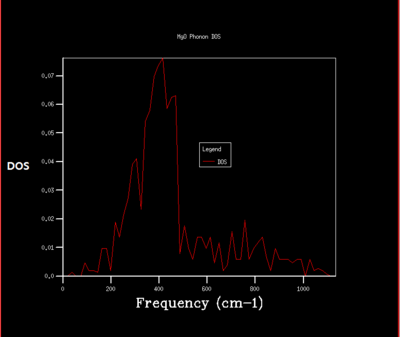
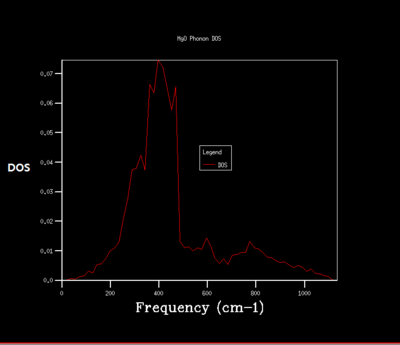
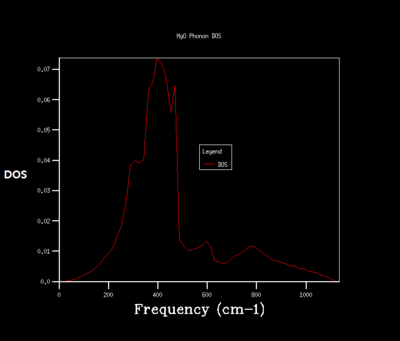
Phonon DOS

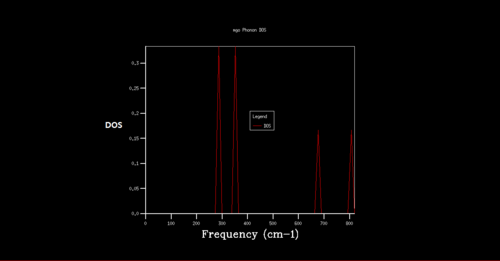
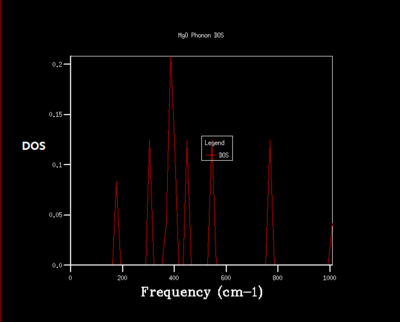
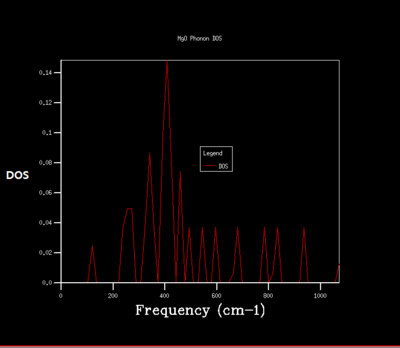
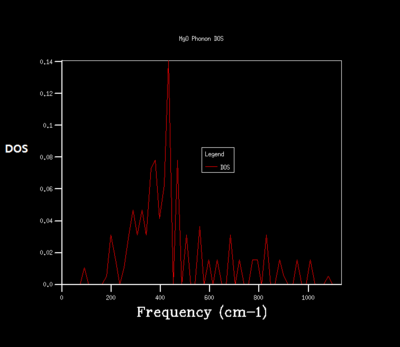
Density of state is the diagram which summate all the states at particular frequency for phonon. Generally, the density of states is proportional to the inverse of the slope of E(k) versus k which means the flatter the band, the greater the density of states at that energy. Using the band structure the shape of the density of states curves can be predicted. The density of states is an average over all k-points resulting the number of vibrational modes at each frequency. ^[2]


Figure 4: Phonon DOS with 1x1x1 shrink factor	Figure 5: Phonon DOS with 2x2x2 shrink factor	Figure 6: Phonon DOS with 3x3x3 shrink factor

Figure 7: Phonon DOS with 4x4x4 shrink factor	Figure 8: Phonon DOS with 8x8x8 shrink factor	Figure 9: Phonon DOS with 16x16x16 shrink factor

Figure 10: Phonon DOS with 32x32x32 shrink factor

As shrinking factor increases the DOS is broadened and smoother. As the grid size increases more of the possible vibrations are sampled and more features appear. The shrinking factor of 32 was determined to be a reasonable grid size. The shrinking factor greater than 32 takes much longer time to be calculated and therefore shrinking factor of 32 gives the optimal number of k points to have an accurate result and 32 grid size is the optimal grid size.

For the shrinking factor of 1x1x1 is computed from a single k-point. Frequencies (cm-1) : 288.49 288.49 351.76 351.76 676.23 818.82 Two frequencies, 288.49, 351.76 are degenerate which is shown from the higher magnitude of two peaks around at 288 and 350 compare to the other two peaks. Using phonon dispersion curve and phonon DOS curve the k-point for the 1x1x1 shrinking factor can be found. And the k- point for the 1x1x1 shrinking factor is L, $K_{L}$ = (0.5 0.5 0.5). $K_{L}$ vector = 0.5a*+0.5b*+0.5c*

This grid size would not be suitable for the bigger or smaller structure. For example zeolite (e.g. Faujasite) is larger primitive cell in real space meaning it would be smaller in reciprocal space. And therefore the optimal shrinking factor would be smaller as fewer k-points would be needed to get accurate DOS diagram. For a metal such as lithium is a smaller primitive cell in real space meaning in reciprocal space it would be larger than MgO and therefore more k-points would be needed to get accurate DOS and larger shrinking factor would be suitable for the calculations.

Calculating the Free Energy in the Harmonic Approximation

The free energy of MgO was computed in the Quasi-Harmonic approximation and the free energy of the crystal can be calculated by summing all the vibrational bands j and all of the k-points over all vibrational energy levels.

Shrinking factors	Helmholtz Free Energy (eV)	Difference from converged energy (eV)
1x1x1	-40.930301	0.003818
2x2x2	-40.926609	0.000126
3x3x3	-40.926432	-5.1E-05
4x4x4	-40.926450	-3.3E-05
8x8x8	-40.926478	-5E-06
16x16x16	-40.926482	-1E-06
32x32x32	-40.926483	0
64x64x64	-40.926483	0

Table 1: Helmholtz free energy for different shrinking factors

The table 1 shows that 2x2x2 grid size is suitable for the calculation within 0.5 meV and 1.0 meV. For the calculation within 0.1 meV, grid size of 3x3x3 is suitable. As the grid size increases the free energy converges to -40.926483 eV. And again the shrinking size of 32 is the optimal grid size considering both efficiency and accuracy.

The Thermal Expansion of MgO

Quasi-Harmonic Approximation

The structure of MgO was optimised with respect to the free energy at several temperatures. The free energy is computed within the quasi-harmonic approximation.
Some assumptions were made for the calculation.

Born- Oppenheimer approximation
No electron – electron interaction
No defects or impurities in the crystal


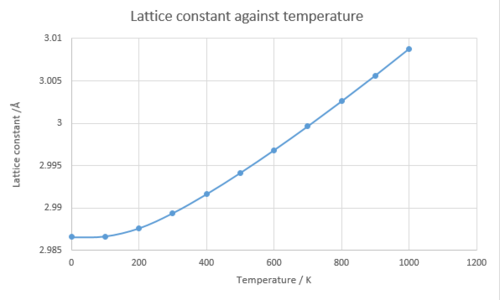
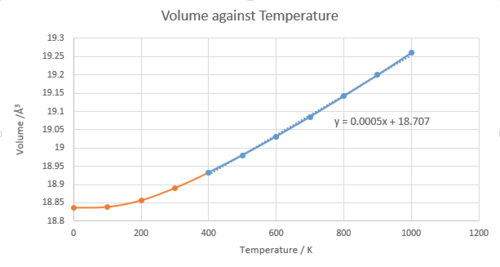
Figure 11: Helmholtz Free energy against temperature using Quasi-Harmonic approximation	Figure 12: Lattice constant against temperature using Quasi-Harmonic approximation	Figure 13: Volume against temperature using Quasi-Harmonic approxmation

Thermal coefficient is calculated from the volume against temperature graph.

$α_{V} = \frac{1}{V_{0}} {(\frac{\partial V}{\partial T})}_{p}$
$α_{V} = \frac{1}{18.836} \times 0.0005$
$α_{V} = 2.65 \times 1 0^{- 5}$

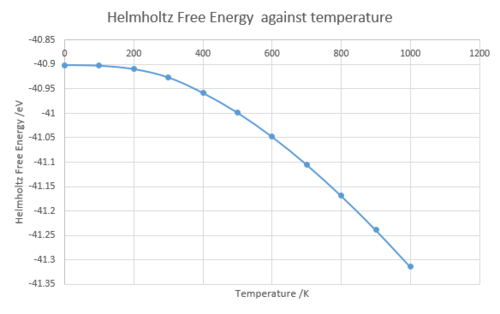
The Helmholtz free energy decreases as the temperature increases because the entropy of the system increases with the increasing temperature.

A= U-TS

And also as the temperature increases the lattice constant increases meaning the volume of the system also increases with the increasing temperature. These three graphs shows that until 400 K the dependency to the temperature is not linear.

The bond length in a diatomic molecule with harmonic potential does not increase with temperature because no bond dissociation is considered in harmonic approximation. Within the Quasi-Harmonic approximation, the bond length increases with the temperature because the position of the harmonic potential changes as the Helmholtz free energy changes and the vibrational frequencies are dependent on the volume. As the temperature increases the kinetic energy increases in the lattice and this leads more accessible higher vibrational levels. And this results more repulsion between atoms leading the increasing in bond length and the volume (thermal expansion). The thermal expansion coefficient can be determined from a gradient of volume against temperature graph. As the temperature approaches to the melting point of MgO using Quasi-Harmonic approximation, the simulation time increases. The system would not consider as lattice to be melted and phase changes but increasing in the volume infinitely due to thermal expansion.

Molecular Dynamics

Molecular Dynamic model is the way to average over all of the vibrational modes of a crystal without using the harmonic approximation. It calculates velocity and position for the lattice crystal. In molecular dynamic model, the timestep is the important parameter. It needs to be long enough for the efficient calculation but short enough for all the possible vibrations of the atoms to be sampled. For this experiment time step of 1 femtosecond (10-15 seconds) was used. At each time step the instantaneous and averaged values of a number of properties are reported. The volume of the unit cell fluctuates from time step to time step, but as the system equilibrates the averaged value become more stable and the average volume was used to calculate the thermal expansion coefficient. The size of the system is also an important parameter for the simulation and 32 units of MgO was used in this experiment. The single unit cannot use for the simulation as the crystal is moving perfectly in phase and the simulation would be the same as sampling the phonons at k = (0, 0, 0). As the units gets larger the simulation would be more accurate, however it takes longer and 32 units of MgO was compromised between the accuracy and efficiency.


Figure 14: Volume against temperature using molecular dynamics model

Thermal expansion coefficient $α_{V} = \frac{1}{V_{0}} {(\frac{\partial V}{\partial T})}_{p}$
$α_{V} = \frac{1}{18.68} \times 0.0006$
$α_{V} = 3.21 \times 1 0^{- 5} K^{- 1}$

Comparison results obtained using Quasi-harmonic approximation and molecular dynamic model


Figure 15: Volume against temperature for the both models

	Thermal expansion coefficient
Quasi-Harmonic aprroximation	$2.65 \times 1 0^{- 5} K^{- 1}$
Molecular dynamics	$3.21 \times 1 0^{- 5} K^{- 1}$

Table 2: Thermal expansion coefficients for two different models

The two graphs show similar behavior from 400 K to 1300 K. As Quasi-harmonic approximation shows parabolic behavior. The thermal expansion coefficient calculated for the Molecular dynamics model is higher than Quasi-Harmonic approximation. The experimental values for the thermal expansion coefficient was $1.45 \times 1 0^{- 5} K^{- 1}$ . ^[3] And this value was calculated at the temperature below than 600 K and therefore it would not be suitable to compare with thermal expansion coefficient values calculated using the result from 0K to 1000 K. The Quasi- Harmonic model is closer to the experimental value giving evidence that it is better model to calculate thermal expansion coefficient for the lower temperature than molecular dynamic model. As the temperature approaches to the melting point of MgO using Quasi-Harmonic approximation, the simulation time increases. Molecular dynamic model shows that the volume increases quite quickly near the melting temperature. 3125.15 k And also the Quasi-Harmonic approximation does not expect the system to have a phase transition and the bond length increases infinitely where the molecular dynamics model can undergo phase transition and again the molecular dynamics model is better for the calculation for higher temperatures.

Conclusion

The thermal expansion coefficient of MgO was studied in this experiment using two different models and the results obtained from two models were compared each other and with literature value. The Quasi-harmonic approximation and the molecular dynamics model were used. These two models approach the thermal expansion coefficient differently and gives different thermal expansion coefficient. From the result the Quasi-harmonic model gives better result for the lower temperature simulations and the molecular dynamics model gives better result for the higher temperatures. However the thermal expansion coefficient values calculated from these two models shows limitations as some assumptions made for both models.

References

↑ Introduction to the Computational Laboratory,Giuseppe Mallia , http://www.ch.ic.ac.uk/harrison/Teaching/Thermal_Expansion/Introduction.pdf, Accessed: March 2017
↑ How Chemistry and Physics Meet in the Solid State, Hoffmann Roald, Angewandte Chemie International Edition in English, Angew. Chem. Int. Ed. Engl, DOI - 10.1002/anie.198708461, Accessed: March 2017
↑ Quantum-mechanical description of ions in crystals: Electronic structure of magnesium oxide, Víctor Luaña, J. M. Recio, and L. Pueyo, Phys. Rev. B 42 1791, Accessed: March 2017

[1] Introduction to the Computational Laboratory,Giuseppe Mallia , http://www.ch.ic.ac.uk/harrison/Teaching/Thermal_Expansion/Introduction.pdf, Accessed: March 2017

[2] How Chemistry and Physics Meet in the Solid State, Hoffmann Roald, Angewandte Chemie International Edition in English, Angew. Chem. Int. Ed. Engl, DOI - 10.1002/anie.198708461, Accessed: March 2017

[3] Quantum-mechanical description of ions in crystals: Electronic structure of magnesium oxide, Víctor Luaña, J. M. Recio, and L. Pueyo, Phys. Rev. B 42 1791, Accessed: March 2017

[1]

[2]

[3]