Rep:Mod:Pew2014

Patricia Woodbridge - Friday, 14^th February 2014

Synthesis Labs: 1C

Part 1

Introduction

The improvement of modern computational techniques in the last two decades have been key in the development of the area known as Computational Chemistry. "Easier to use" programs and cheaper computers have made it a more accessible and useful technique compared to the increasing cost of experimental apparatus and laboratory equipment. This does not mean that it could completely replace the traditional investigation method, but that it can now be a used as a valuable tool side by side with other practical techniques in research areas within Physical, Inorganic and Synthetic Chemistry.

Computational chemistry can be used as a tool for visualising molecules and calculating their energy minimum. As well as this it can predict NMR, IR, UV-Vis or optical rotation spectroscopy and it can model transition states in a chemical reaction.

Using a theoretical and mathematical approach rather than experimentally obtained data, Computational Chemistry has now become a fundamental way of acquiring very detailed molecular analysis from Quantum Chemistry. Wherever the Quantum Mechanic approximations prove to complex to be calculated even by a computer, Molecular Mechanics can be a useful technique to avoid complicated and long calculations that can arise when analysing big molecules.

This report is an example of different ways in which computational chemistry can be a useful tool for a research project or a practical experiment.

Hydrogenation of cyclopentadiene dimer

Fig.1 Mechanism for the dimeristaion of cyclopentadiene

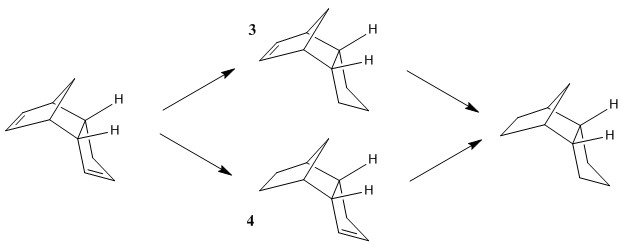
The dimerisation of cyclopentadiene is a concerted cycloaddition between a two ciclopentadienes, one acting as a diene and the other as a dienophile. This reaction gives rise to different stereo-chemical outcomes depending on how both molecules approach each other(Fig.1). The exo approach results from a the dienophile approaching the diene from away, whereas the endo product will result from a direct-on-top approach. Both products can be analysed with computational techniques to determine which is the most stable product in terms of overall energetic configuration. The drawback of this techniques is that the relative energies of the transition state intermediates cannot be calculated. This means that although we could predict the reaction outcome based on which is the product with lowest energy (and therefore most stable), the product that we get from a practical experiment might be the opposite if its transition state has a much lower energy. This is actually the case for the dimerisation of cyclopentadiene: the product with lowest energy is the exo dimer (thermodynamic product) however the experimental outcome of the reaction gives exclusively the endo product (the kinetic product).

Both molecules where modelled using ChemBio3D and then their energies where calculated using Avogadro (molecular mechanics approach: MMFF94s). The results are recorded in Table.1. The main energy contribution is due to the angle bending strain. In the case of the endo product, this energy is higher: ΔE_{angle bending}=2.49kcal/mol, the rest of the energy contributions are very similar and therefore nothing indicates why would the endo product be favored over the exo product.

The unexpected stereo-chemical outcome can be rationalised by discussing the relative orientation of both cyclopentadienes during the transition state. The endo addition involves a plane-to-plane orientation which allows favorable iterations between occupied and unoccupied orbitals, lowering the energy of its transition state. These interactions are nonexistent during the exo approach therefore the only energy stabilisation results from the lower bending angle energy present in the product.

Table 1 - Energies of products resulting of the dimerisation of cyclopentadiene, the dihydrogenated products and the tetrahydrogenated product

MMFF94s Energy minimisation (kcal/mol)	Exo Dimer (1)	Endo Dimer (2)	Dihydro (3)	Dihydro (4)	Tetrahydro
Bond stretching	3.54317	3.45521	3.28713	2.83642	2.73050
Total Angle Bending Energy	30.77261	33.25875	32.02942	24.68526	25.15303
Total Stretch Bending Energy	-2.04143	-2.08203	-2.10142	-1.66283	-1.67673
Total Torsional Energy	-2.73104	-2.96437	-1.57937	-0.40721	1.28440
Total out-of-plane Bending Energy	0.01476	0.01726	0.01360	0.00024	0.00000
Total Van der Waals Energy	12.80168	12.31850	13.67882	10.67185	11.55090
Total Electrostatic Energy	13.01367	14.18982	5.11982	5.14649	0.00000
TOTAL ENERGY	55.37342	58.19314	50.44800	41.27022	39.04210

Fig.2 hydrogenation of cyclopentadiene dimer

File:Pew11 - Compound 3.pdf For the hydrogenation of the dimer, a step-wise reaction (as seen in figure 2) leads first to the saturation of one of the double bonds and then finally to the saturated final product. The same method was used as before and compounds 3 and 4 were modeled using ChemBio3D and their energy calculated using MMFF94s energy calculation with Avogadro. The results are also summarised in table 1. The results of this analysis show how, unlike with the dimerisation of cyclopentadiene, where the kinetic product is formed, the hydrogenation of the dimer follows a thermodynamic controlled reaction. Literature reports that the product mostly formed is compound (4) before the final product is formed. By observing the results, we can conclude that the the main issue with the energies of both compounds 3 and 4 is the angle bending energies and the Van der Waals interactions, which lead to the conclusion that compound 3 is more strained than compound 4. By visually analysing the modeled structures of compound 3 and compound 4 this can be explained. If both molecules are viewed from this angle (see screen shot 1, left), we can see how the angles of the upper molecule (3) varies most from the ideal 120deg between C-C-H angles in double bonds (giving rise to higher bending angle energy), and also how compound 3 has the most staggered conformations (i.e. higher Van der Waals interactions - although the difference is not large).

Atropisomerism in an intermediate related to the synthesis of Taxol

Fig.3 Taxol intermediates compound 9 and compound 10

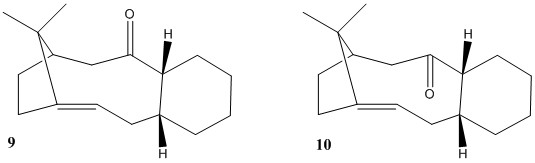
File:Pew11 - Doc1.pdf Paclitaxel, commercially known as Taxol, is an anticancer drug used to treat breast, lung, neck and ovarian cancer. Its synthesis involves the formation of compound 9 and 10, two atropisomers shown in Fig.3. The difference between them is the relative orientation of the carbonyl. Energy minimisation was carried out using MMFF94s molecular mechanics on Avogadro, and after several attempts to minimise the overall energy, two different energy minimas where found for each atropisomers depending on the conformation of the fused cyclohexane. The results of this analysis are summarised in table 2. As expected, both atropisomers in which cyclohexane had a chair conformation where lower in energy than the twist-boat conformation, and overall, compound 10 was more stable.

In both atropisomers, its twist boat conformation for the fused cyclohexane shows a higher torsional strain and Van der Waals energy interaction relative to the chair conformation. And overall, it is the strain caused by the angle bending that has the highest effect on the total energy. Again by visual comparison (see screen shot 2), we can see this. Sp3 carbons ideally form 109deg angles, therefore compound 9 must have the structure furthest away from this number. Further analysis of this structure shows that the carbons surrounded by a circle in the screen shot (between carbonyl carbon and bridging group) are the ones that suffer most deviation and therefore the ones that contribute the most to the angle bending strain. As before, Van der Waals interactions can also be analysed (again, see screen shot 2). And also show a higher energy interaction not only between the fused cyclohexane and the carbons furthest to the left, but also between the O lone pairs and the bridging carbons. This interaction is slightly alleviated in the structure of compound 10.

Table 2 - Energies of Taxol intermediates

MMFF94s Energy minimisation (kcal/mol)	9 (chair conformer)	9 (twist boat conformer)	10 (chair conformer)	10 (twist boat conformer)
Bond stretching	7.67653	7.94889	7.59178	7.73875
Total Angle Bending Energy	28.27616	29.49713	18.79864	19.58258
Total Stretch Bending Energy	-0.07653	0.08171	-0.14383	-0.06008
Total Torsional Energy	0.21455	2.76801	0.24949	3.19219
Total out-of-plane Bending Energy	0.97159	0.95349	0.84963	0.85320
Total Van der Waals Energy	33.17541	34.72124	33.25828	35.05675
Total Electrostatic Energy	0.29983	0.31678	-0.05243	-0.04537
TOTAL ENERGY	70.53755	76.28726	60.55155	66.31802

The alkene seen in compounds 9 and 10 tend to be very unreactive. Their location (next to a bridge) make the atoms less strained than the equivalent saturated hydrocarbon would be. This is know as a "hyperstable" olefin, which essentially explains the decreased reactivity of these functionalities. The reason behind this remarkable stability is that bridgehead alkenes have more favourable bonds than their equivalent bridgehead alkanes, giving lower bending angle strain and therefore making them more stable (bridgehead C in medium/large rings are "flattened out", making the ideal angle closer to sp2-like carbons rather than sp3-like)..

Spectroscopic simulations using Quantum Mechanics

Fig.4 Taxol intermediate derivatives: compound 17 and compound 18

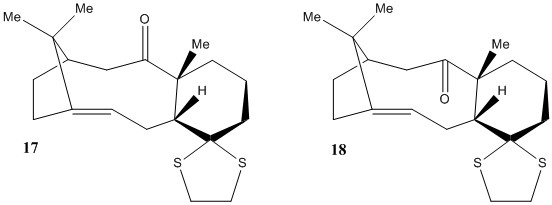
Another very useful technique is the ability to generate spectroscopic data from modeled molecules. In this exercise, two derivatives of the Taxol intermediate seen before were analysed to see which was more stable and then the ¹H NMR and the ¹³C NMR were computed (using the HPC system) and compared to literature. These simulations were done using Gaussian assuming Chloroform was used as solvent.

Compound 17 and 18 (fig.4) were modeled using ChemBio3D and their relative energies were optimised using Avogadro (compared in Table 3). This time, only the conformer with fused cyclohexane in the chair conformation was modeled. As expected from the analysis carried out in the previous exercise, Compound 18 was more stable. Although it must be noted that the difference in energy was now much lower, most likely due to the extra methyl group present next to the carbonyl carbon which possibly strains the angles more than the previous hydrogen and does not allow much difference between the C angles in both atropisomers.

Table 3 - Energies compound 17 and 18 - Taxol intermediates derivatives

MMFF94s Energy minimisation (kcal/mol)	Compound 17	Compound 18
TOTAL ENERGY	104.82348	100.49043

The resulting ¹H NMR and ¹³C NMR data have been tabulated below in table 4 and 5, and the spectra can be seen in figures 5 and 6. Several things however had to be taken into account, especially for ¹H NMR when comparing to literature values. Hydrogen that are in the same environment due to rapid bond rotation are computed as if they were in different environments when the HPC computes the spectra, therefore when compared to the literature the integrals appeared to not match up initially. In the tables, it has been taken into account. ¹³C NMR on the other hand is very accurate and shows good correlation with expected environments.

Fig. 5 - Predicted ¹³C NMR for Compound 18

Table 4 - ¹³C NMR Summary and comparison to literature

Predicted NMR chemical shift (ppm)	Literature NMR chemical shift (ppm)
214.520	211.49
146.987	148.62
119.297	120.90
86.006	74.61
56.570	60.53
55.134	51.30
51.505	50.94
49.802	45.93
49.292	43.28
45.318	40.82
42.519	38.73
42.030	36.78
39.211	35.47
35.240	30.84
31.893	30.00
28.435	25.56
26.428	25.35
25.045	22.21
22.471	21.39

Fig. 6 - Predicted ¹H NMR for Compound 18

Table 5 - ¹H NMR Summary and comparison to literature

Predicted NMR chemical shift (ppm)	Literature NMR chemical shift (ppm)	Integration
5.924	5.21 (m, 1H)	1
3.268	3.00-2.70 (m, 6H)	1
3.216		1
3.137		1
3.026		1
2.868		1
2.768		1
2.525	2.70-2.35 (m, 4H)	2
2.333		1
2.667		1
2.207	2.20-1.70 (m, 6H) 1.58 (t, J=5.4Hz, 1H) 1.50-1.20 (m, 3H) 1.10 (s, 3H) 1.07 (s, 3H)	1
1.991		4
1.860		2
1.774		1
1.668		1
1.600		2
1.494		2
1.300		1
1.211		1
0.959	1.03 (s, 3H)	3

This method also allows a vibrational analysis (that would also allow a UV-Vis spectra or an IR spectra) that can calculate the free energy of the molecules.

• For molecule 17: ΔG= -1651.4612 Hartree
• For molecule 18: ΔG= -1651.4723 Hartree

The difference is equal to: 0.0111 Hartree = 29.143kJ/mol, which shows how much more stable compound 18 is.

Part 2

Introduction

Fig.7 trans-β-methylstyrene epoxidation

Fig.8 1,2-Dihydronaphthalene epoxidation

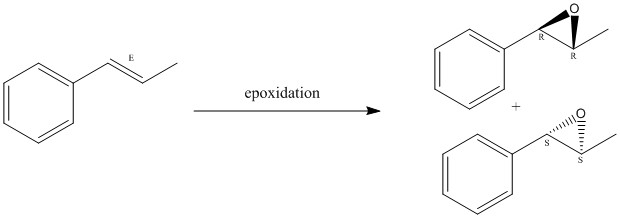
The second part of this report, is about using computational chemistry side by side with a synthetic project carried out in the Labs (experiment 1S). Two catalysts were synthesised and then several epoxidations were carried out. In this report, the main focus is set on the epoxides and determining their absolute configuration. As seen in figures 7 and 8, the two alkenes chosen to undergo epoxidation are: 1,2-dihydrophthalene and trans-β-methylstyrene. They both yield two different products.

Catalyst structure analysis

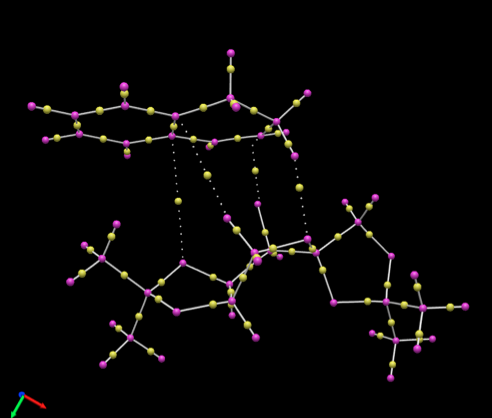
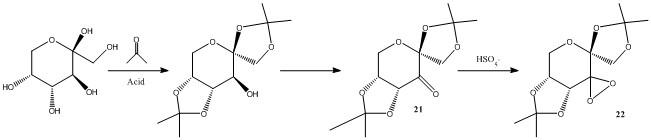
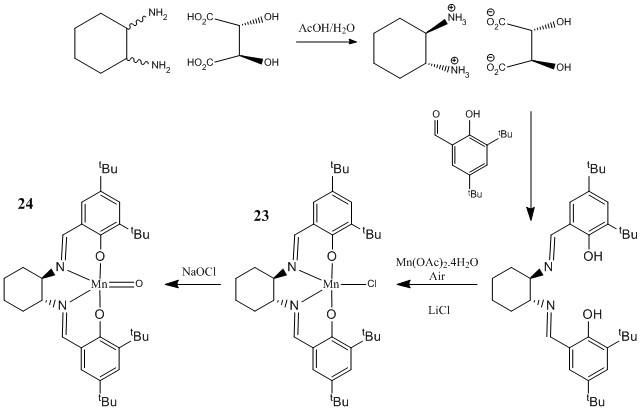
The structure of the Shi Catalyst (22) and the Jacobsen Catalyst (24) can be seen in figures 9 and 10. Searching the Cambridge Crystal Database (CCD) using ConQuest program, both pre-catalyst structures (21) and (23) where found and their structures where analysed with the Mercury program. Several aspects of their structure where measured.

The Shi asymmetric fructose catalyst

Fig.9 Synthesis of Shi Catalyst (22) Via stable intermediate (21)

Shi Pre-Catalyst (21): C-O bond lengths for anomeric OCO centers

The first catalyst to discus is the Shi Catalyst, a derivative of D-fructose. Its pre-catalyst (21) has 3 anomeric centers (marked in blue on the left. The different bond lengths of these anomeric carbons have been measured and are shown in the interactive image. If there was any anomeric interaction occurring, different bond lengths between the Oxygens in the same center would be expected, as one of them would experience an inductive effect due to the favourable overlap of the oxygen lone pair into the antibonding C-O sigma orbital and therefore one of the CO bonds would be shorter than expected whereas the other CO bond would be longer (as electron density would be dumped into it antibonding orbital). This does not occur at the anomeric centre furthest from the oxane group in the six membered ring, or at the anomeric centre next to the carbonyl. Both bond lengths are almos identical (Δlength=0.002Å). However, a larger difference is observed in the last anomeric center, where the difference is now 0.006Å (three times as much). Therefore it can be assumed that the anomeric effect only occurs in this OCO anomeric centre.

The Jacobsen asymmetric catalyst

Fig.10 Synthesis of Jacobsen Catalyst (24) via pre-catalyst (23)

Shi Pre-Catalyst (21): C-O bond lengths for anomeric OCO centers

The molecular Structure of the Jacobsen pre-catalyst (23) was also modeled and as before, the CCD was searched. In this case however, it is interesting to compare the different distances between the ^tBu groups in the molecule. These distances have been measured out and can be seen in the interactive image above. The closest ^tBu groups are the ones closest but in the different aromatic rings. The ideal Van der Waals distance between two Hydrogens is 2.40Å (Van de Waals radii of H= 1.20Å). So in fact, the two ^tBu groups are within the range of the Van der Waals attractive interaction which will overall stabilise the molecule. The other two ^tBu groups are not within Van der Waals attractive region.

In all the Jacobsen catalyst is extremely bulky and can only bind to small and not bulky alkenes.

Product NMR

Following the catalyst analysis, the ¹³C NMR and the ¹H NMR of the possible epoxides where simulated using the predicting software used previously for the Taxol derivative. Molecules where modeled using ChemBio3D, energetically optimised using MMFF94s Avogadro and then the Gaussian program was used to predict the spectras in chloroform.

The predicted values for the ¹H NMR (as before) needed to be accounted for degenerate hydrogen environments, but besides that all the data was quite accurate and similar. All the results have been summarised in tables 6, 7, 8 and 9 and the spectra are shown in figures 11, 12, 13 and 14.

β-methyl styrene

Fig. 11 - Predicted ¹³C NMR for trans-β-methylstyrene oxide

Table 6 - ¹³C NMR Summary and comparison to literature

Predicted NMR chemical shift (ppm)	Literature NMR chemical shift (ppm)
134.975	137.9
124.072	128.6
123.328	128.2
122.796	125.7
122.727
118.486
62.320	59.7
60.576	59.2
18.838	18.1

Fig. 12 - Predicted ¹H NMR for trans-β-methylstyrene oxide

Table 7 - ¹H NMR Summary and comparison to literature

Predicted NMR chemical shift (ppm)	Literature NMR chemical shift (ppm)	Integration
7.500	7.20-7.40 (m,5H)	1
7.496		2
7.476		3
7.422		1
7.307		1
3.415	3.57 (d, 1H, J=2.1 Hz)	1
2.788	3.03 (qd, 1H, J=5.1 Hz, 2.1 Hz)	1
1.678	1.45(d, 3H, J=5.1 Hz)	1
1.587		1
0.717		1

1,2-dihydronaphthalene

Fig. 13 - Predicted ¹³C NMR for 1,2-dihydronaphthalene oxide

Table 8 - ¹³C NMR Summary and comparison to literature

Predicted NMR chemical shift (ppm)	Literature NMR chemical shift (ppm)
135.388	137.1
130.37	132.9
126.666	129.9
123.791	128.83
123.533	128.80
121.744	126.5
52.821	55.5
52.192	55.2
30.180	24.8
29.063	22.2

Fig. 14 - Predicted ¹H NMR for 1,2-dihydronaphthalene oxide

Table 9 - ¹H NMR Summary and comparison to literature

Predicted NMR chemical shift (ppm)	Literature NMR chemical shift (ppm)	Integration
7.615		1
7.391	7.34 ( 1H, d J=7.2 Hz)	1
7.387	7.09-7.25 (2H , m)	2
7.251	7.02 (1H, d J=7.2 Hz)	1
3.559	3.66 (1H, J=4.4 Hz)	1
3.483		1
2.947	2.64-2.70 (1H, m)	1
2.267	2.47 (1H, dd J=5.6 Hz, 15.6 Hz)	1
2.209	2.29-2.37 (1H m)	1
1.873	1.62-1.73 (1H, m)	1

Absolute configurations of the products

Finally, to analyse the absolute configuration of the epoxides, their Optical Rotation was simulated also using Gaussian. The results where quite interesting (summarised in table 10). Enantiomers have the same physical and chemical properties except their optical rotation. Because they are mirror images of each other, they polarise the light in opposite directions, therefore their Optical Rotation (OR) will be of opposite sign. In the case of 1,2-dihydronaphthalene oxide, the modeled structure was the (1R, 1S) enantiomer, however most of the literature values only report the (1S, 1R) enantiomer, and that is why it has similar value to the literature reported but opposite sign.

Table 10. Optical Rotation values

	1,2-dihydronaphthalene epoxide	trans-β-methylstyrene epoxide
Predicted OR (deg)	52.76 (1R,2S)	-103.06 (S,S)
Literature OR (deg)	-39 (1S,2R)	-116 (S,S)

Active site interactions of the reaction transition states

Kinetically controlled reactions undergo via the less energetic transition state. Analysis of the ΔG energy of the different transition states of each enantiomers and conformers of the alkene allows to predict the major product and the enantiomeric excess. The way to do this is by acquiring the molar Gibbs energy (which is the sum of the electronic and thermal free energies) calculated from the entropy and the zero-point energy correction.

Epoxidation via Shi catalyst can have four different transition states, depending on which of the two dioxyrane Oxygen in compound (22) (which are planar with respect to the rest of the molecule) is attached for the epoxidation and depending the orientation on how it approaches (exo or endo). The oxygen that will be attached will be the one with least double bond character

Epoxidation via Jacobsen catalyst (24) can only have two different transition states according to the two different approaches (exo or endo). The Oxygen in the Mn=O bond will be the one that is transferred and the possible orientation will depend on how the phenyl ring is situated during the binding.

So each epoxides will have two possible enantiomeric outcomes that can have four (if catalysed by Shi) or two (if catalysed by Jacobsen catalyst) transition states. All of these transition states will have different energies, so if for a given epoxide, the two lower energy transition states for each possible enantiomer is subtracted, K can be found by using the equation ΔG=RTlog(K). With known K, the enantiomeric percentage will be equal to %=(K-1)/(K+1). The enantiomeric percentage give the ratio of the favoured enantimer.

1,2-dihydrophthalene oxide

Epoxidation with Shi Catalyst

(R,S) enantiomer is favoured, as seen from ΔG energy of transition states.

Table 11 - Transition state calculations of K and enantiomeric excess

Δ=lowest (RS)- lowest(SR)	K	Enantiomeric excess
-12.287341	1477.8368	99.797%

Epoxidation with Jacobsen Catalyst

(S,R) enantiomer is favoured, as seen from ΔG energy of transition states.

Table 12 - Transition state calculations of K and enantiomeric excess

Δ=lowest (SR)- lowest(RS)	K	Enantiomeric excess
5.8548654	704.18291	99.716%

trans-β-methylstyrene

Epoxidation with Shi Catalyst

(R,R) enantiomer is favoured,as seen from ΔG energy of transition states.

Table 11 - Transition state calculations of K and enantiomeric excess

Δ=lowest (RR)- lowest(SS)	K	Enantiomeric excess
-9.5305657	1146.2708	99.826%

Epoxidation with Jacobsen Catalyst

(S,S) enantiomer is favoured,as seen from ΔG energy of transition states.

Table 12 - Transition state calculations of K and enantiomeric excess

Δ=lowest (SS)- lowest(RR)	K	Enantiomeric excess
-10.5833913	1272.89745	99.843%

Non-Covalent interactions

Gaussview can also simulate the Non-covalent interactions occurring during the transition states of the epoxidations. These interaction are H-bonding interactions, electrostatic interactions and dispersion forces.

By creating an image such as the one seen bellow (taken from ), any non-covalent interactions appear as clouds of different colour (blue is very attractive, green mildly attractive, yellow mildly repulsive and red is strongly repulsive).

Electronic Topology

The image above corresponds to the lowest energy transition state of the (S,R) naphthalene epoxidation using the Shi catalyst. The yellow spheres represent high electron density (possible bond formation). Together with the NCI analysis it gives a greater look at the mechanisms of transition states. The discontinuous lines observed between both molecules correspond to weak-non-covalent Bond critical points which are all due to covalent interactions between C and O.