Rep:Mod:Peebo
Introduction
Overview
Fundamental to organic chemistry are pericyclic reactions that involve concerted movement of electrons through a cyclic transition state. Cycloadditions, a subset of pericyclic reactions, serve as a essential synthetic tool for organic chemists as a basis for accessing more complex structures in, for example, total synthesis of natural products [1]. In addition, sigmatropic rearrangements, and electrocyclic reactions are also a set of important pericyclic reactions that see Δσ 0 or ±1 respectively. For Diels alder and ene reactions, the initial arrangement of the fragments is brought into question when trying to understand the stereochemical outcome of the reaction. Other than these geometric factors, the frontier orbitals of the two fragments contain valuable information into predicting whether the two reactants may proceed to reach a product[2].
Robert Burns Woodward and Roald Hoffman established rules to explain whether a given pericyclic reaction may be thermally or photochemically allowed to give the said product. Naturally incorporated in their approach is considerations of the molecular orbitals involved in the reaction, the number of electrons, and the symmetry with respect to the connectivity between the two fragments. First applied to electrocyclic reactions [3], the two would then go on to publish more papers to fully develop their rules setting a universal foundation for understanding these class of reactions
Given the wealth factors that contribute towards going from reactants --> products, it is of the best interests to synthetic chemists to understand the mechanistic basis behind the reaction and therefore ,for example, the observed stereochemistry as opposed to whether a given reaction may be allowed or forbidden (in conjunction with Woodward-Hoffman rules). As such, computational methods into investigating diels alder reaction pathways have come to light[4][5] and have shown to provide insight into the optimal positioning of fragments and the structure and energy of Transition states. Studying transition states in particular are a huge advantage in computational studies; through this medium, calculations on energies of these states can be probes that would otherwise be immeasurable due to the fleeting nature of the transition state.
Experimental Aims
In this exercise, we first investigate the energies of varying 1-5 hexadiene conformers and investigate the possible cyclic transition states whilst it undergoes the cope rearrangement using the Hartree-Fock/3-21G and B3LYP/6-31G(d) levels of theory in addition to exploring Transition state optimization methods QTS2 and TS(Berny). Using similar methods, we then go on to develop our discussion of transition states by through investigating the regioselectivity of the Diels Alder reaction between maelic anhydride and 1-3 cyclohexadiene including molecular orbital interactions.
Brief note: Computational Methods
In this investigation, we explore different levels of theory to apply alongside our calculations as each have both advantageous features, and their respective drawbacks. Hatree fock method is used to determine both energies and quantum mechanical wavefunction of a multi-body system in state that has its probability density (position of the body in question) independent of time (i.e a stationary state). Amongst the appreciable number of approximations made by this method, the assumption that many electron wavefunction of the body in question will take the form of a just an isolated determinant (slater determinant) derived from a single electron wavefunction. Whist in theory this is entirely possible through linear combination of atomic orbitals, this naturally causes this approach to overlook the replusive interactions between the electrons in the system thus producing energies that are overestimated.
By virtue The Hohenberg-Kohn Theorems, the total energy of a ground state is exclusively dependent on electron density and distribution. Focusing in on this aspect and overlooking the electronic wavefunctions give rise to density functional theory. This method will aim to minimize energy via changes in electron density in a body. In addition to this, Electron correlations are taken into account and the mean field approximation is relaxed However, one key drawback in this theory is that it is not certain that using a more complicated basis set my necessarily produce a more accurate answer; the theory is not variational whereas the HF theory actively is.
Nf710 (talk) 15:51, 21 January 2016 (UTC) Excellent understanding of the variation principle. good intro
The Cope rearrangement: Computational Investigations
Overview
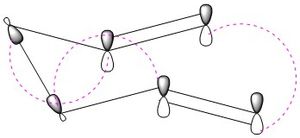
1-5 hexadiene provides a relatively simple system to observe a cope rearrangement. Through Woodward-Hoffmann analysis, we see that this [3,3] sigmatropic rearrangement is thermally allowed by virtue of the equation (4q + 2)s + (4r)a. Figure 2 provides one way in which the reaction can proceed via these rules with a single σ2s component and two π2a components.
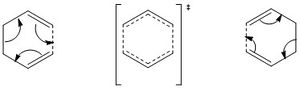
During the concerted formation/dissociation of bonds, the transition state resembles that of a six membered ring which can exhibit a chair or boat topology (in line with the conformers of cyclohexane) These transition states represent energy maxima on the reaction pathway from reactants to products. On the other hand, 1-5 hexadiene exists in many conformers representing an energy minimum. In the following section, we obtain optimal structures for the diene on different levels of theory followed by locating the position of the TS on the potential energy surface. In doing this, we can appropriately deduce the activation energy involve in the cope rearrangement through the chair TS and boat TS pathways.
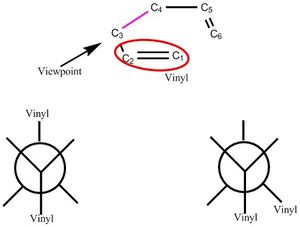
Optimizing reactants and products
The substrate under investigation can adopt many different conformers with respect to the central C3-C4 bond as seen in figure 3. Within the conformers laid out in the diagram exists a subset of more isomers that differ in the exact positioning of the vinyl group relative to the rest of the molecule as opposed to just the other vinyl group. Initiative would serve to think the antiperiplanar set of isomers would be of lower energy than the gauche type isomers purely on the argument of steric repulsion between the two vinyl groups. Various conformers of Hexadiene the consist of gauche and antiperiplanr motifs were optimized and the results posted in the table below. The nomenclature of conformers are with respect to appendix 2
Nf710 (talk) 15:59, 21 January 2016 (UTC) very good understanding of the mechanistics of the reaction.
| placeholder | Gauche3 | Anti2 | Anti1 | Gauche(1) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Image | ||||||||||||
| Energy (Hartres) | -231.69266122 | -231.69253516 | -231.69260235 | -231.68771610 | ||||||||
| Point Group | C1 | Ci | C2 | C2 | ||||||||
| log | file | file | file | file |
In comparison with literature reference values there is very good agreement. Interestingly, the lowest energy conformer reveals itself as a gauche type conformer which is contrary to initial predictions. Visualizing the molecular orbitals indicates favorable electronic interactions in the gauche3 setup; the two pi systems of the vinyl groups are in close enough proximity to yield a favourable in phase overlap which isn't possible in the anti conformation purely on the grounds of spacial arrangement. The gauche3 conformer serves as a balance between repulsive steric interactions and attractive molecular orbital-overlap interactions.
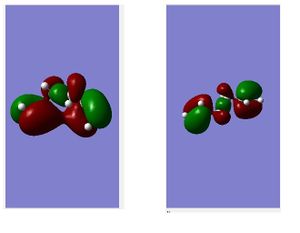
Nf710 (talk) 16:11, 21 January 2016 (UTC) Good use of both set of oribitals to explain the overlap
We can now approach the optimization of hexadiene on a different level of theory. The HF_3-21G optimized anti2 conformer of the alkene was then re-optimized under DFT_6-31G(d) level of theory. The geometrical differences arising form these two different methods of computation are summarized below.
| |||
|---|---|---|---|
| HF/3-21G | B3LYP/6-31G* | ||
| Bond Lengths (Angstrom) | C1-C2 | 1.32 | 1.33 |
| C2-C3 | 1.51 | 1.50 | |
| C3-C4 | 1.55 | 1.55 | |
| Bond Angles (Degrees) | C1-C2-C3 | 124.80 | 125.29 |
| C2-C3-C4 | 111.34 | 112.65 | |
| C1-C2-C3-C4 | 114.63 | 118.58 | |
Being immediately observable is the increase in bond length with the B3LYP/6-31G* level of theory in comparison to HF/3-21G. Within the same level of theory however, the HF/3-21G method describes less of a distinction between bond lengths of C-C single bonds and C-C double bonds. This may also be detectable by running frequency calculations and visualizing the vibrations involving the C=C bonds in both conformers.
frequency investigations
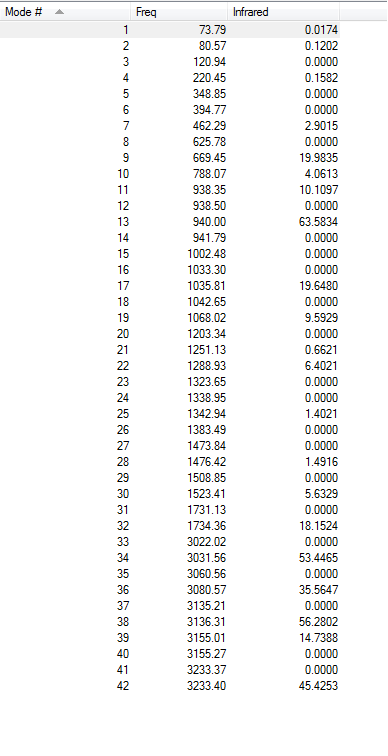
Frequency analysis of the B3LYP/6-31G* optimised structure was carried out. Gaussian carries out this procedure by applying the equation for force constants 
(where C = 1/2π) and preforming calculations to see a convergence in the force constant. The absence of imaginary frequencies would indicate that we have indeed reached a true minimum on the potential energy surface. A summary of the optimisation is given below
| Frequency summary | Spectrum |
|---|---|
 |
|
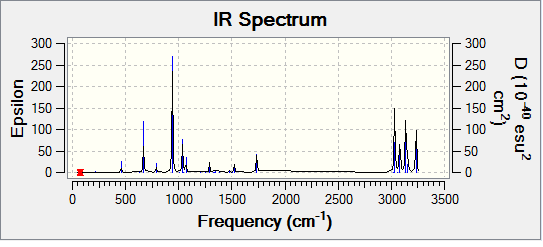The thermodynamic properties were noted post-optimisation and printed as follows (units in Hartrees)
Sum of electronic and zero-point Energies= -234.469213 Sum of electronic and thermal Energies= -234.461864 Sum of electronic and thermal Enthalpies= -234.460920
Transition state investigations
Overview
Having processed information about the reaction reactants/products, we can now try to approach mining information about a different area on the potential energy surface; the transition states.
As eluded to earlier, the reaction proceeds via a 6 membered ring transition state that can exhibit a boat or chair toplogy. In this section, we aim to find these states on the potential energy surface, assess their energies and consequently determine the activation energy involved in both pathways. We will start by building and optimising the fragments of the transition states, and running further frequency/optimisation calculations.
Defining a transition state requires a degree of appreciation for the reaction mechanism being explored. In this case, the two allyl fragements that will be used need to exhibit sensible geometry to allow for a completed freq + opt calculation to be run to completion. Two different methods of computing the transition state are explored in this section. In the first method, the frozen coordinates approach is taken. This involves locking the reaction coordinate whilst minimisation of the rest of the molecule is performed (through any method of choice including Hf/3-21G, B3LYP/6-31G* levels of theory). Another optimsation can then be run which will optimize the rest of the molecule.
The second approach involves calculating the force constant along the reaction coordinate with both the number of steps along the coordinate and the direction to run the calculation both being defined by the user. In this approach however, It is important that the guess structure of the transition state is quite close to the actual case.
To start this investigation, the frozen coordinate methods were applied.
The Chair
After optimising an single allyl (CH2CHCH2) through the HF/3-21G level of theory (log file here), two of the said fragments were arranged in a chair conformation, with terminal C-C bond distance (between two fragements) set to 2.2 Å
HF/3-21G allyl fragment |
This "guess" transition state was then run through an Frequency + Optimisation job (the log file of which can be located here) introducing the TS(Berny) optimisation method. This method works by employing the Berny algorithm. An approximate Hessian matrix (constituted by calculating second derivatives of energy) is developed using parameters of the initial structure including the valence force field. this approximation is then updated by calculating energies along the reaction pathway until a convergence is observed. Thus, the approximate matrix is a key factor in determining the success of the calculation. For most cases, using the approximate hessian serves well for the rest of the optimisation of the molecule, but in the cases where the the hessian changes dramatically, the force constant can be computed along every point of the reaction pathway. At the expense of time and computational power, the opitmisation will be able to find the local minimum.
Guess Transition state vibration mode |
Inspection of the vibrations shows a single imaginary frequency (negative cm-1) at -817.94 cm-1 This "guess structure" method provides a reference/basis to which the frozen method can be compared with.
Imaginary frequencies are given such names due to the complex nature of their absolute values. Eigenvalues of hessian matrices correspond to squared harmonic oscillations of the normal vibration modes. thus a the square root of a negative eigenvalue gives rise a complex number with an imaginary component. Taking a simple plot of the harmonic oscillator (potential energy vs bond displacement), a negative second derivative would indicate that the geometry to which the reaction coordinate is abiding by is hitting a maximum (i.e. achieving transition state status). Thus if a transition state has been calculated, only one imaginary frequency should be as a result of the optimisation.
The frozen coordinate approach was then used to compute the transition. The (to be formed) bond between the terminal C's on both allyl fragments were strictly fixed/frozen to 2.2 Å followed by an optimisation. The log file can be found here. Having optimised the rest of the molecule with the mentioned bonds of interest fixed, the bonds will be accounted for in a second optimisation to which the log file can be found here
To summarize, the chair transition state has be investigated through a reference setup and an frozen coordinate setup. The table of results below give an account of the results of the two setups.
| ||||||
| Guess TS | Frozen TS | |||||
|---|---|---|---|---|---|---|
| Terminal C-C Bond Length (Angstrom) | 2.02 | 2.02 | ||||
| C1-C2/C2-C3 bond length | 1.39 | 1.39 | ||||
| C-C-C angle | 120.50 | 120.49 | ||||
| jmol | ||||||
The Boat
Having exhausted the chair TS, computations in the Boat conformer will be brought under investigation. In this section, more computational methods that investigate transition states will be explored. The QTS2 methods works by using user defined reactants and products and attempts to conceive new data points via interpolation such to find the transition state between them. The substrate was setup and labelled to depict reactants and product and was subsequently processed with the QTS2 method. The resultant log file can be found here
Having run this initial calculation, the geometries of the reactants and products were edited to resemble that of a boat transition state. The same calculation was run again ( log file here) The results of the two runs are summarized in the table below.
| Arbitrary | Boat-Like | |||||
|---|---|---|---|---|---|---|
| jmol | ||||||
| Terminal C-C bond length (Angstrom) | 2.02 | 2.14 | ||||
| C1-C2/C2-C3 bond length | 1.39 | 1.38 |
Nf710 (talk) 16:15, 21 January 2016 (UTC) What was the frequency?
Endpiece: Comparing the Boat & Chair
To conclude this section of the study, the transition states will be optimised using the Intrinsic reaction coordinate (IRC) method. Arguably the defining feature of this approach is the ability to track the reaction coordinate from the transition state to a local minimum by taking minute steps along negative,steep gradients of the potential energy surface. This bears many favourable features for users to define at will namely defining how many steps to be taken in the calculation and the direction of the gradient should run from the transition state.
The IRC method was applied to the optimised chair conformer. The resultant log file can be found here.
The same molecule was then further optimised to find a minimum under the HF/3-21G level of theory. The resultant log file can be found here
As seen by the the results of re-optimisation post-IRC, the conformer best represent that of the gauche2 state supported by the point group being C2. To allow activation energies to be calculated, a gauche 2 conformer was constructed and optimised under the HF/3-21G level of theory (log file here) followed by the B3LYP/631G* level of theory (log file here) The thermochemical data can then be retrieved and be used as the reactants on the reaction coordinate pathway. Thus the difference in energy between the gauche2 conformer and the boat and chair transition states can be calculated
Lastly, optmised chair and boat structures were re-optimised under the a higher level of theory (B3LYP/6-31G*) with the resultant log files presented here and there respectively
Nf710 (talk) 16:21, 21 January 2016 (UTC) You have identified the correct conformer
Nf710 (talk) 16:42, 21 January 2016 (UTC) You must have run out of time. The things you did, you did well, and you showed a good understanding of the methods used
The Diels Alder Cycloaddition: Computational Investigations
(You're missing a lot from this section. Did you run out of time? Tam10 (talk) 16:16, 12 January 2016 (UTC))
Overview
Simple Systems: S-cis butadiene and ethene
As an introduction to a cycloaddition, the reaction between ethene and butadiene was investigated. setting the two vinyl protons in the same plane (i.e C1C2C3C4 dihedral angle = 0), the molecule was optmised under the Semi empirical am 1 method. Similarly, a molecule of cis-butadiene was optimised. The table below shows the results of optimisation
| Ethene | S-cis butadiene | |||||
|---|---|---|---|---|---|---|
| Jmol | ||||||
| Point Group | C2v | d2h | ||||
| HOMO |  |
| ||||
| LUMO |  |
| ||||
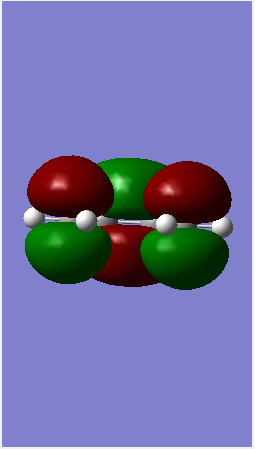
| LOG files | file | file |
following reactant optimisation,the fragments were arranged into a guess transition state (using the same concepts explored in the cope rearrangement investigations. The terminal Carbons on each fragment was fixed to be 2.2 angstrom apart. The resultant TS structure had a single imaginary frequency confirming formation of a transition state. The log file for optmisation can be found here.
(This Jmol applet is empty. It seems you've put the filename outside of a tag. I've put the corrected Jmol below with the vibration Tam10 (talk) 16:16, 12 January 2016 (UTC))
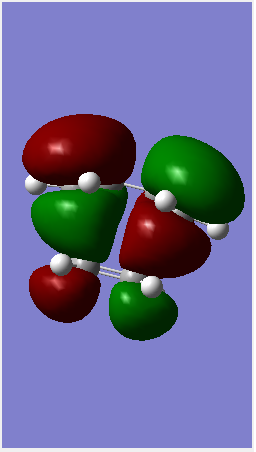
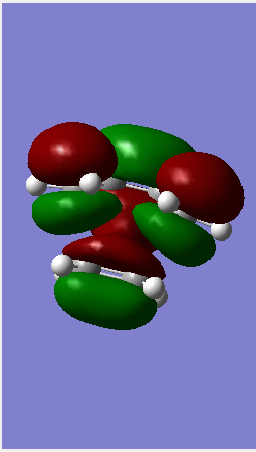
Complex systems: Maelic anydride and Cyclohexadiene
Using the same concepts explored in the cycloaddition investigations with the two unfunctionalised alkenes, the properties of the Diels Alder reaction between Maleic anhydride and cyclohexa-1,3-diene was investigated. As we will see, the regiochemistry of the reaction comes into play as the arrangement of the two subtrates prior to bond making/breaking gives rise to two different trasnition states (an exo and an endo state). Obtaining Molecular orbital data for of the two states will account for differences in the observed energies of the transition states.
the two reactants were optimised under the Semi empirical am1 method. The results of the calculations are presented in the table below
Optmising the reactants| Maelic anhydride | Cyclohexadiene | |||||
|---|---|---|---|---|---|---|
| Jmol | ||||||
| Point group | C2 | C1 | ||||
| HOMO |  |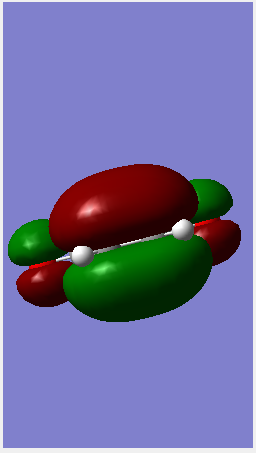
| ||||
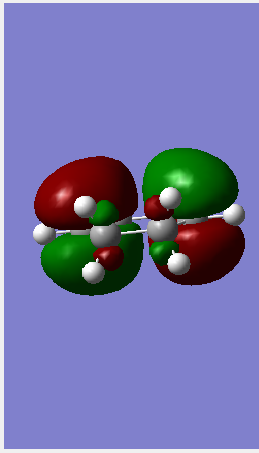
| LUMO |  |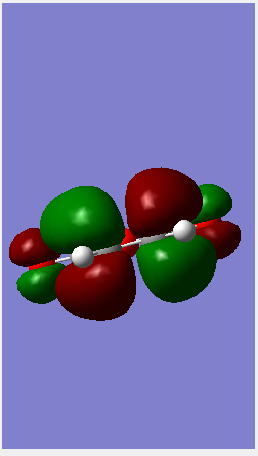
| ||||
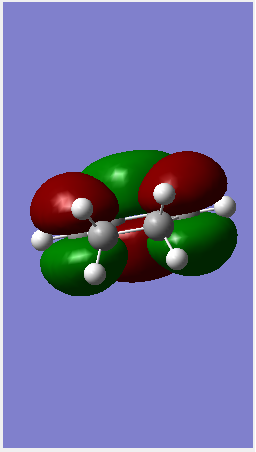
| LOG | file | file |
As per routine, a guess transition structure had to be constructed using the optimised fragments. In this case, we have stereo-distinction between two possible transition states, and exo form and an endo form.
For both endo and exo forms, terminal C-C bond distances were set and fixed to 2.2 Angstrom and the molecule adapted to represent a postulated transition state fro the respective forms. an optimisation + frequency calculation was carried out an the results given below
Log files || file || file| Exo transition state | Endo Transition state | |||||
|---|---|---|---|---|---|---|
| Jmol | ||||||
| HOMO |  |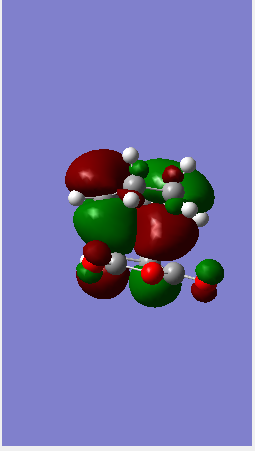
| ||||
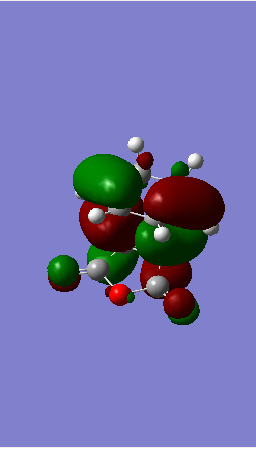
| LUMO |  |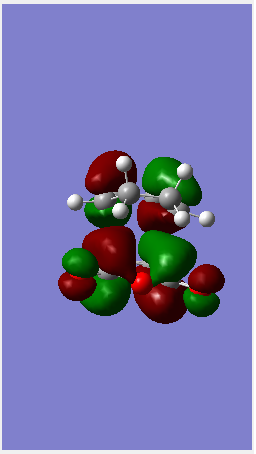
|
Geometry data for the two states was also collected. The results are presented below
| Exo transition State | Endo Transition state | |||
|---|---|---|---|---|
 |
| |||
| bond | values (Angstrom) | bond | values (Angstrom) | |
| C1-C2 | 1.41 | C1-C2 | 1.49 | |
| C2-C3 | 1.49 | C4-C5 | 1.49 | |
| C5-C1 | 1.49 | C5-C1 | 1.41 | |
| C2-C9 | 2.17 | C1-C9 | 2.16 | |
| C1-C6 | 2.17 | C5-C6 | 2.16 | |
| C6-C7 | 1.34 | C6-C7 | 1.49 | |
| C7-C8 | 1.40 | C7-C8 | 1.52 | |
| C8-C9 | 1.39 | C8-C9 | 1.49 | |
| C9-C10 | 1.49 | C9-C10 | 1.39 | |
| C10-C11 | 1.52 | C10-C11 | 1.40 | |
| C11-C6 | 1.49 | C11-C6 | 1.49 | |
Lastly, thermochemical data was collated and the results given below
Exo
Sum of electronic and zero-point Energies= 0.134882 Sum of electronic and thermal Energies= 0.144882 Sum of electronic and thermal Enthalpies= 0.145826 Sum of electronic and thermal Free Energies= 0.0991180.099118
Endo
Sum of electronic and zero-point Energies= 0.133494 Sum of electronic and thermal Energies= 0.143683 Sum of electronic and thermal Enthalpies= 0.144628 Sum of electronic and thermal Free Energies= 0.097350
To end this section on the more complex systems, the overall energy of the Endo transition state is lower than that of the exo (refer to the log file for the energies). This is due to the so called secondary orbital overlap effect. Looking at the image of the HOMO in the endo state there is possible overlap between orbitals on the Oxygen including the lone pairs and the pi system on the cyclodiene
References
[1] K. Takao, R. Munakata, K. Tadano, Chem. Rev. 2005, 105, 4779−4807 [2] K. N. Houk, J. Am. Chem. Soc., 1973, 95, 4092–4094 [3] R. B. Woodward, R. Hoffman, J. Am. Chem. Soc., 1965, 87, 395–397 [4] M. Manoharan, F. De Proft, P. Geerlings, J. Org. Chem., 2000, 65, 7971–7976 [5] M. Svensson, S. Humbel, R. D. J. Froese, T. Matsubara, S. Seiber, K. Morokuma, J. Phys. Chem., 1996, 100, pp 19357–19363