Rep:Mod:PY3HS

The Cope Rearrangement

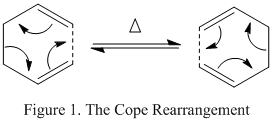
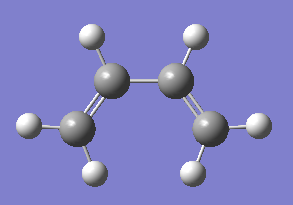
The Cope rearrangement is defined as a pericylic reaction. It was discovered in 1940 by Arthur Clay Cope, and is a thermally driven, symmetry allowed, [3,3]-sigmatropic rearrangement. According to the Woodward-Hoffman rules, it occurs with a suprafacial Hückel topology, as the system contains 6 pi electrons which corresponds to 4n+2 and due to the requirement of heat to proceed. In 1,5-hexadiene an allyl group migrates, from the terminal of the molecule causing a bond to break and a bond to be made (Figure 1).

The product of the Cope reaction is a thermal isomer of the starting material. In the case of 1,5-hexadiene, the reaction is named the degenerate Cope rearrangement, because one can see the thermal isomer is the same as the starting material. This means the driving forces to create either starting material or product are the same and the equilibrium lies directly in the middle, not favoured towards one direction. There is prerequisite that the diene has a cis geometry to allow the pi structures to be in close proximity.

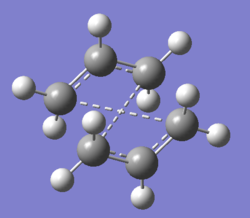
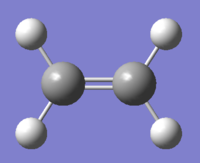
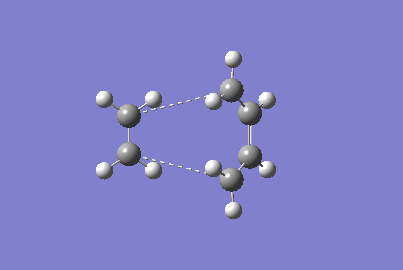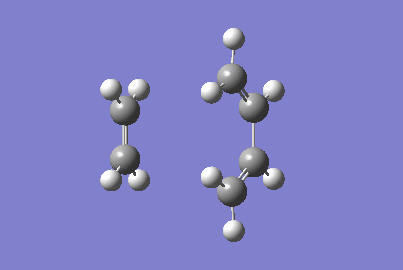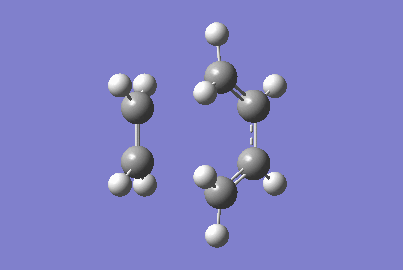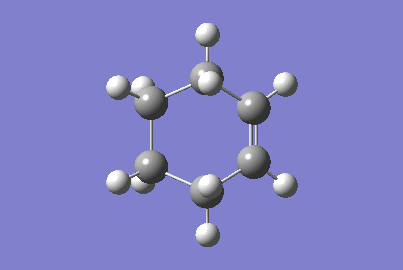
There are two transition states available for the reaction, the chair and the boat transition states. Their structures are shown in the figure below. The reaction is thought to proceed more favourably through the chair transition state

The aim of this study was to model the components of the Cope rearrangement, namely the reactants and transition states, and optimise them to obtain correct structures. Studies will then be carried out, using different levels of theory to confirm presence of transition state structures and to decide which transition state is in fact the most stable. The mechanism of the bond formation and bond breaking in the reaction will also be confirmed.

Optimizing the Reactants and Products

1,5-hexadiene: Antiperiplanar Conformation

A molecule of 1,5-hexadiene was modelled using Gaussview, with an antiperiplanar alignment of the central 4 carbon atoms (highlighted in yellow in the model below). This means the dihedral angle between these atoms is 180^o. Its geometry was optimised using the Hartree Fock/3-21G level of theory. The model and energetic results of this optimisation are shown in Table 1.

Table 1. Summary for antiperiplanar conformation

File Type	.chk	anti conformer
Calculation Type	FOPT
Calculation Method	RHF
Basis Set	3-21G
Charge	0
Spin	Singlet
Total Energy	-231.69260235 a.u./-145389.33408424 kcal/mol
RMS Gradient Norm	0.00001824 a.u.
Dipole Moment	0.2021 Debeye
Point Group	C2

The molecule was symmetrised to determine the point group, in this case C₂.

1,5-hexadiene: Gauche Conformation

1,5-hexadiene was drawn using Gaussview once again, however this time with a gauche conformation of the central 4 carbon atoms. The gauche alignment introduces a modified dihedral angle of 60^o between the central 4 atoms (highlighted in yellow below). The model was optimised using the Hartree Fock/3-21G level of theory. Below is a table summarising the energetic results and the molecule.

Table 2. Summary for gauche conformation

File Type	.fch	anti conformer
Calculation Type	FOPT
Calculation Method	RHF
Basis Set	3-21G
Charge	0
Spin	Singlet
Total Energy	-231.69266120 a.u./45389.3710132 kcal/mol
RMS Gradient Norm	0.00001556 a.u.
Dipole Moment	0.3409 Debeye
Point Group	C1

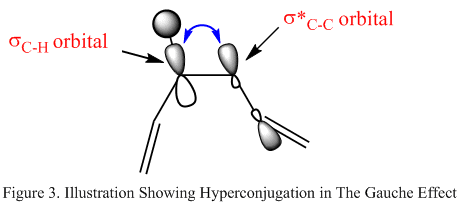
Here after symmetrising the molecule, the point group was determined to be C₁. Upon initial observation of the molecules themsevles, it would be expected that the gauche conformer would lie higher in energy than the antiperiplanar molecule. This is because of steric hindrance that would be experienced by the close proximity of the terminal olefin groups. The proximity is caused by the 60^o dihedral angle of the central atoms. Unexpectedly, comparisons of the total optimised energy shown in table 1 and 2 does not support this theory, as the anti conformer is higher in energy than the gauche conformer. The hydrogen atoms on the 2 central carbon atoms in the gauche conformer are aligned in a staggered arrangement whereas they are ligned up in the anti conformation. This could explain the extra stability of the gauch conformation, as this arrangement maximises the favourable Van der Waals interactions between the hydrogen atoms, whereas in the anti conformer there is higher A^1,3 strain. Another theory is the Gauche Effect, where the alignment of the bonds allows hyperconjugation to occur between the bonding δ_C-H orbital of one central carbon atom into the antibonding δ*_C-C orbital of the other (figure 3 - the overlap is shown as the blue arrow). The gauche conformation maximises this overlap causing extra stability in the molecule. It is favourable because the δ*_C-C orbital is a better electron acceptor due to its energy level.

Using [Appendix 1] from the computational script, it can be confirmed that the two molecules modelled above are the anti1 and the gauche3 conformations. This is evident from the extremely close values of total energy after optimisation and the identical point groups obtained after symmetrising the molecules.

The Lowest Energy Conformation

In total there are 10 different conformers altogether available to 1,5-hexadiene. 6 of these are gauche conformers and 4 are anti conformers, which all differ in their point group and total energies. The conformers that have been optimised, anti1 and gauche3, are in fact the lowest in energy in their conformation group. The difference between them is explained above. The stability of these molecules is determined by a mixture of stereoelectronic and steric effects. Therefore the stability of the anti1 and gauche3 conformations above the others in the groups is determined by the balance between the orientation of particular groups to maximise favourable orbital overlap and the proximity of the olefin groups within the favourable Van der Waals region, causing steric repulsions. For example, the gauche3 conformer is the lowest gauche conformer because it is the one where the olefin groups are the furthest apart from each other.

C_i Antiperiplanar Conformation

The previous optimisations were carried out using the Hartree Fock/3-21G level of theory, a method with a low level of theory. A higher level of theory is the B3LYP/6-31G* level, a density functional theory (DFT). It differs from Hartree Fock methods as its total computed energy is the sum of 6 different contributing energies, one of which isn't included in the HF method. This makes comparisons of energies of molecules between the 2 levels of theory impossible. The anti2 conformation, according to [Appendix 1] of the computational script, was modelled on Gaussview, cleaned up and was subsequently optimised using both the Hartree Fock/3-21G level of theory and B3LYP/6-31G* in order to compare. This conformer differs from the previously modelled anti1 conformer due to the angle of the olefin groups with respect to the rest of the molecule. It is higher in energy than anti1, however is relatively low compared to the remaining 8 conformations.

HF/3-21G Computations

The results and model of the Hartree Fock optimisation is shown below in Table 3.

Table 3. Summary for HF anti2 conformation

File Type	.fch	anti2 conformer
Calculation Type	FOPT
Calculation Method	RHF
Basis Set	3-21G
Charge	0
Spin	Singlet
Total Energy	-231.69253525 a.u./ -145389.29197834 kcal/mol
RMS Gradient Norm	0.00001897 a.u.
Dipole Moment	0.0005 Debeye
Point Group	Ci

It can be confirmed that the resulting molecule is in fact the anti2 conformation as its total energy is extremely similar to the one found in [Appendix 1] of the computational script. The point group, C_i, determined after symmetrising is also identical to this reference.

B3LYP/6-31G* Computations

To carry out this density functional theory method, the already optimised molecule using the HF method above was used.

Table 4. Summary for B3LYP/6-31G* anti2 conformation

File Type	.fch	anti2 conformer
Calculation Type	FOPT
Calculation Method	RHF
Basis Set	6-31G(D)
Charge	0
Spin	Singlet
Total Energy	-234.61171035 a.u./ -147221.10240112 kcal/mol
RMS Gradient Norm	0.00001373 a.u.
Dipole Moment	0.0000 Debeye
Point Group	Ci

As discussed above, one cannot compare energies resulting from the two different level of theories as they contain different contributions. Other parameters therefore need to be compared, however these differ only very slightly. The bond lengths of the 2 optimised structures are shown in the models above. They are almost exactly the same apart from the C=C double bond is slightly longer, at 0.133nm, and the adjacent C-C single bond is slightly shorter at 0.15nm in the B3LYP/6-31G* optimised molecule. The symmetry of the molecule did not change upon re-optimisation at this level of theory as the point group remains at C_i. Therefore overall there are very insignificant changes that occured.

Frequency Analysis and Thermochemical data

The resulting energy from the B3LYP/6-31G* optimisation represents the total energy of the molecule when it lies on the bare potential energy surface (PES). Therefore the location of the molecule on this surface can be determined as being a minimum or a maximum. A maximum would represent an intermediate or transition state and therefore the desired position would be a minimum. In order to verify this, a frequency calculation can be carried out upon the B3LYP/6-31G* optimised anti2 conformation, at the same level of theory. The calculation was run on Gaussian where the job type was modified from an optimisation to a frequency calculation. The vibrational spectrum resulting from this computation is shown below:

If this molecule is a minimum on the PES then the evaluated frequencies from the calculation will all be real and positive. The lowest frequency calculated for this molecule was at 74.29, a real and positive value, which is the same for all the other calculated frequencies. Therefore it can be confirmed that it is in fact a minimum. The lowest vibrational frequency corresponds to the two olefin groups moving from side to side, either side of the plane of the molecule, simultaneously.

298.15 K

The thermochemistry parameters are also evaluated during this frequency calculation. The job was run at 298.15 K and the results are shown in table 5 below. The table also shows what each value means in terms of energy contributions and conditions.

Table 5. Thermochemistry Data for anti2 at 298.15 K

Sum of electronic and zero-point Energies	-234.469204	E = Eelec + ZPE calculated at 0K
Sum of electronic and thermal Energies	-234.461857	E = E + Evib + Erot + Etrans calculated at 298.15 K and 1atm
Sum of electronic and thermal Enthalpies	-234.460913	H = E + RT
Sum of electronic and thermal Free Energies	-234.500777	G = H - TS

Here the energies are relatively similar, the largest difference being ~-0.1 Hartrees.

0 K

The frequency analysis was run on the anti2 conformation but at 0 K. The lowest vibration was also at 74.29cm-1 corresponding to the same motion and therefore the simulated vibrational spectrum was identical. The resulting thermochemical energies are shown in table 6.

Table 6. Thermochemistry Data for anti2 at 0 K

Sum of electronic and zero-point Energies	-234.469204	E = Eelec + ZPE calculated at 0K
Sum of electronic and thermal Energies	-234.469204	E = E + Evib + Erot + Etrans calculated at 298.15 K and 1atm
Sum of electronic and thermal Enthalpies	-234.469204	H = E + RT
Sum of electronic and thermal Free Energies	-234.469203	G = H - TS

Here all the contributions are the same value ~-234.469204. The sum of electronic and zero-point energies value at 0 K is the same as for at 298.15 K because this parameter is measured at 0 K anyway. The sum of electronic and thermal energies is the same as this value because at 0 K there would be no motion in the molecule, therefore the Evib + Erot + Etrans contributions are essentially 0, just leaving E =E. The sum of electronic and thermal enthalpies correction, H = E + RT, is temperature dependent therefore H = E, and this is the same case for the sum of electronic and thermal free energies where G = H, and therefore G = E.

Optimizing Chair and Boat Transition State Structures

Allyl Fragments

From figure 2, it is clear that each transition state consists of 2 C₃H₅ allyl fragments orientated in a specific manner to one another. Therefore in order to optimise a chair and boat transition state structures, an allyl fragment was drawn in Gaussview and optimised using the HF/3-21G level of theory. The resulting structure is shown on the right.

Optimised Allyl Fragment

Chair Transition State

The optimised allyl fragment structure was copied to obtain 2 fragments which were subsequently rotated and translated with respect to one another to represent a chair transition state structure, similar to the one shown in [Appendix 2] of the computational lab script. The distance between the two terminal carbons of each allyl fragment was set to 2.2Å (shown below as the blue highlighted atoms). This distance was chosen because a typical C-C bond length is 1.54Å therefore for a transition state this length would have to be above this value. The structure was defined as the 'guess structure'. There are 3 different ways to obtain and optimise transition state structures. Two of them, 'Hessian' and 'Frozen Coordinates', are described below for the chair transition state.

Hessian Method of Optimisation

This method is accurate when the guess structure of the transition state is very close to the correct structure. It optimises by computing the force constant matrix which is continuously updated during the optimisation procedure. The guess structure created previously was optimised by changing the Job Type to Opt+Freq, to obtain vibrational information which is useful in determining whether the result is in fact a transition state. Instead of optimising to a minimum the guess structure optimised to a transition state, using TS (Berny). The force constants were calculated once during the procedure and the Additional Word: Opt=NoEigen was included. This additional word ensures that the computation doesn't crash if there is more than one imaginary frequency detected, which is characteristic of transition states. The results of the optimisation are shown in table 6.

Table 7. Hessian Chair Transition State Optimisation

File Type	.chk
Calculation Type	FREQ
Calculation Method	RHF
Basis Set	3-21G
Charge	0
Spin	Singlet
Total Energy	-231.61932244 a.u./ -145343.35023664 kcal/mol
RMS Gradient Norm	0.00001429 a.u.
Imaginary Frequency	-817.96cm-1
Dipole Moment	0.0005 Debeye
Point Group	C2h

Using [Appendix 2] from the computational script, it is clear that the chair transition state has been obtained. The distance between the 2 terminal carbons on each allyl fragment has been optimised to 2.02Å and the overall point group of the transition state is C2h. There is also an imaginary frequency at -817.96cm-1 which is characteristic of this transition state. This is worked out using second derivatives, therefore the negative value proves it lies at a maximum and not a minimum on the PES. This particular vibration has been animated in the model in table 7 and is the correct vibration corresponding to the Cope Rearrangement.

Frozen Coordinates Method of Optimisation

The frozen coordinate method of optimisation is ideal when the guess structure is far from the actual structure of the transition state. It works by 'freezing' the reaction coordinate first and then optimising the rest of the molecules to a minimum. Once this has been done, the coordinates can be unfrozen and then the whole model can be re-optimised together, however this time to a transition state. The calculation was carried out upon the chair transition state guess structure again, where the distance between the 2 terminal carbon atoms of the allyl fragments were set to 2.2Å. Using the Redundant Coordinate Editor on Gaussview, the coordinates corresponding to one terminus of the allyl fragments was frozen and the same was subsequently done for the other terminus. An optimisation was then run, to a minimum, using the Hartree Fock method and the default basis set 3-21G, with these coordinates frozen. The result of this optimisation is shown below: Frozen Coordinates

The model looks very similar to the transition state obtained using the Hessian method. However this time the distance between atoms 6 and 11, and 4 and 14 were fixed at 2.2Å. These are the frozen coordinates. Using this optimised structure, the coordinates were then unfrozen by using the Redundant Coordinate Editor on Gaussview. This was done by selecting the previously frozen coordinates and changing the key word from Add to Derivative. When the caculation was set up in this instance, the optimisation was run to a transition state, using TS (Berny), instead of a minimum and the HF/3-21G level of theory was chosen. The force constants here were never calculated so the calculation could be run along the derivative of the chosen coordinates. The results of this are shown in table 8. Relaxed Coordinates

Table 8. Frozen Coordinates Chair Transition State Optimisation

File Type	.log
Calculation Type	FTS
Calculation Method	RHF
Basis Set	3-21G
Charge	0
Spin	Singlet
Total Energy	-231.61932233 a.u./ -145343.35016761 kcal/mol
RMS Gradient Norm	0.00002128 a.u.
Imaginary Frequency	-817.89cm-1
Dipole Moment	0.0002 Debeye
Point Group	C2h

The resulting structure is identical to the structure obtained using the Hessian method. The distances between atoms 6 and 11, and atoms 3 and 14 are 2.02Å and after symmetrising the structure the point group was determined to be C2h. These details coincide with the Hessian method and [Appendix 2] of the computational script. A frequency analysis was run on the structure, using the HF/3-21G level of theory to confirm it was a transition state. An imaginary frequency is observed at -817.89 cm-1, similar to the Hessian optimised transition state. The vibration corresponding to this value also indicates the Cope Rearrangement.

Boat Transition State

The boat transition state of the Cope Rearrangement will be optimised using the third possible method, QST2.

QST2 Method of Optimisation

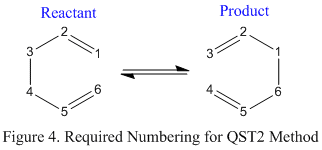
This method involves using input structures for the reactants and products for a particular reaction and the calculation will try to find a structure inbetween them that corresponds to the transition state. The prerequisite for this method is that the atom numbering is the same in the reactants and the products. In the case of 1,5-hexadiene the product and the reactant are the same, however still, as shown in figure 4, the atom numbering must be manually changed for the calculation to proceed correctly. Molecule 1 and 2 represent the reactant and product respectively. The renumbering below was carried out by editing the atom list using Gaussview.

To set up the QST2 calculation, the Job Type was set to Opt+Freq and the Hartree Fock with default basis set 3-21G level of theory was used. The optimisation part was set to a transition state, however this time to TS (QST2) optimisation. This minimisation failed and instead of the boat transition state, a somewhat dissociated chair-like transition state of the Cope Rearrangement was formed. This is shown below. It is thought that this occurs because the calculation only uses translation for the top allyl fragment and doesn’t consider rotation that would take place between the central 2 carbon atoms. Thus the input reactant and product molecules for this particular calculation are not ideal to locate the boat transition state.

To obtain the correct transition state structure, the anti2 conformation was modified to look more similar to the boat transition state. The dihedral angle between the 4 central carbon atoms (2, 1, 6, 5) was set to 0ᴼ and that between the inside 3 carbon atoms (2, 1, 6 and 1, 6, 5) was set to 100ᴼ. Once again there is a prerequisite of numbering the atoms in the product to match the reactants. These structures are shown below, and indicate a closer representation to the boat transition state than the previous input molecules.

Product	Reactant

The QST2 calculation was set up once again, using the same Job Type (Opt+ Freq), the same level of theory (HF 3-21G) and the same minimisation to TS (QST2). This time the optimisation was successful and the boat transition state structure was obtained. The energetic summary and a model of this are shown in table 9.

Table 9. QST2 Boat Transition State Optimisation

File Type	.chk
Calculation Type	FREQ
Calculation Method	RHF
Basis Set	3-21G
Charge	0
Spin	Singlet
Total Energy	-231.60280248 a.u./ -145332.98380301 kcal/mol
RMS Gradient Norm	0.00003469 a.u.
Imaginary Frequency	-840cm-1
Dipole Moment	0.1582 Debeye
Point Group	C2v

After symmetrising the model, its point group was determined to be C2v. This, and the structure of the transition state, coincides with [Appendix 2] of the computational lab script. The distance between the 2 fragments has been optimised to 2.14Å and from the frequency analysis included in the optimisation, a resulting imaginary frequency is found at -840cm^-1. This allows confirmation of the presence of a transition state. The animation corresponding to this particular imaginary frequency is shown in the table above. It can be seen that this represents the bond breaking and bond formation that occurs in the Cope Rearrangement.

In conclusion, the optimised chair transition state is lower in energy than the optimised boat transition state. This is expected as the chair conformation contains staggered alignments of the bonds throughout which experiences less steric strain than the boat conformation, which contains eclipsed alignments throughout. Analysis of the QST2 method of optimisation shows that although it can be useful, it is still necessary that the input structures of reactant and product resemble the desired transition state to an extent.

Intrinsic Reaction Coordinates (IRC)

Upon initial observation of the optimised transition state structures, it is not possible to predict exactly which conformer of 1,5-hexadiene will result at the end of the thermal rearrangement. The Intrinsic Reaction Coordinate (IRC) is a method implemented in Gaussian which allows the minimum energy path of the reaction coordinate to be followed down to a minimum on the potential energy surface, after the transition state occurs. This of course will correspond to the product of reaction. Gaussian does this calculation by following the specific direction that has the steepest energy gradient around the transition state.

The chair transition state structure that was optimised using the frozen coordinates method was used for the IRC. The Job Type under the calculation setup menu was altered to the IRC option. There is an option the compute the reaction coordinate in both the forward and reverse direction. As the product and reactant in this specific reaction are identical, only the forward direction was chosen to be calculated. The force constants were always calculated during the calculation and the number of points to be evaluated along the reaction coordinate was set initially at 50. The calculation was run using the default HF 3-21G method. The results of the IRC calculation are shown below in the form of an animation. Chair Transition State IRC

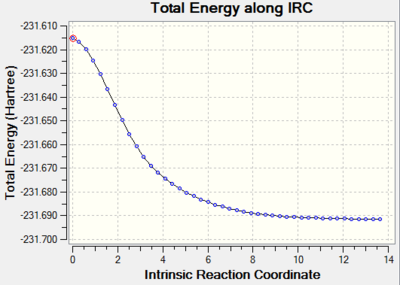
From the IRC graph shown above, you can see that the reaction coordinate hasn’t reached a minimal geometry yet. Additionally neither the energy of this structure or its point group matches any of the conformations available to 1,5-hexadiene ([Appendix 1]). One option would be to run the IRC calculation once more but increase the number of points included along the reaction coordinate. This however will prove useless as the previous calculation terminated at only 44 points. This indicates that increasing this value further than 50 will have no effect on this geometry. Instead the last point on the IRC can be minimised with the hope that the changes in geometry upon minimisation will represent the final minimum product geometry. The success of this is dependent upon how close the last structure on the IRC is to the structure of the reaction product, otherwise a different minimum energy path will potentially be followed.

The final coordinate was minimised using the HF 3-21G level of theory. Due to the close total energy values and the identical point group of the optimised structure, it can be confirmed as Gauche 2, using [Appendix 1] of the computational script. After frequency analysis of this structure, there are no negative imaginary frequency and the lowest vibrational frequency is at 65.53 cm^-1. The table below shows a summary of the results of this optimisation.

Table 10. Summary for Optimisation of Last IRC Coordinate

File Type	.chk	anti conformer
Calculation Type	FOPT
Calculation Method	RHF
Basis Set	3-21G
Charge	0
Spin	Singlet
Total Energy	-231.69266700 a.u./-145389.37465273 kcal/mol
RMS Gradient Norm	0.00001395 a.u.
Dipole Moment	0.3800 Debeye
Point Group	C2

Activation Energies

The essential parameters to calculate the activation energy are available from the thermochemistry data provided by a frequency analysis of the appropriate structures, namely the sum of electronic and zero-point energies, and the sum of electronic and thermal energies. Experimental activation energies for the Cope Rearrangement of 1,5-hexadiene at 0 K are 33.5 ± 0.5 kcal/mol for the chair transition state and 44.7 ± 2.0 kcal/mol for the boat transition state. Frequency calculations were carried out on both the boat and chair transition state structures and the anti2 reactant conformer, using both the HF 3-21G and B3LYP/6-31G* levels of theory, in order to obtain these values. This was to compare which level of theory gave the closest match to the experimental values and therefore which method is more reliable for this type of analysis. The results are shown in the tables below.

Table 11. Thermochemistry Data in Hartrees

	Hartree Fock Method			B3LYP/6-31G* Method
	Electronic Energy	Sum of electronic and zero-point energies 0 K	Sum of electronic and thermal energies 298.15 K	Electronic Energy	Sum of electronic and zero-point energies 0 K	Sum of electronic and thermal energies 298.15 K
Chair Transition State	-231.6193224	-231.466699	-231.46134	-234.5569829	-234.414932	-234.409011
Boat Transition State	-231.6028025	-231.450928	-231.445299	-234.5430931	-234.402342	-234.396008
Anti2 Conformation	-231.6925353	-231.53954	-231.532567	-234.6117104	-234.469204	-234.461857

Table 12. Thermochemistry Data in kcal/mol

	Hartree Fock Method			B3LYP/6-31G* Method
	Electronic Energy	Sum of electronic and zero-point energies 0 K	Sum of electronic and thermal energies 298.15 K	Electronic Energy	Sum of electronic and zero-point energies 0 K	Sum of electronic and thermal energies 298.15 K
Chair Transition State	-145343.2094	-145247.4368	-145244.074	-147186.6178	-147097.4796	-147093.7641
Boat Transition State	-145332.843	-145237.5404	-145234.0081	-147177.9018	-147089.5792	-147085.6046
Anti2 Conformation	-145389.1511	-145293.1452	-145288.7696	-147220.9598	-147131.5357	-147126.9254

Table 13. Activation Energies

	Hartree Fock Method		B3LYP/6-31G* Method
	0 K	298.15 K	0 K	298.15 K
Δ Chair	45.70838307	44.69558354	34.05616845	33.16134061
Δ Boat	55.60482751	54.76145541	41.95650676	41.32084014

Firstly the geometry of the transition states were extremely similar between the optimisations using both levels of theory. The tables above confirm that the B3LYP/6-31G* method gives a better match to the experimental activation energies at 0 K, with values at 34.05616845 and 41.95650676. An additional observation would be that all activation energies leading to the chair transition state, despite which calculation method was utilised, are lower in energy than the for the boat transition state. This is as expected as the bond angles in a chair conformation are much closer to the ideal 109.5° sp³ angle, whereas the boat conformation angles are far from this. This puts the chair conformation at a lower energy and therefore renders it the most stable structure.

The Diels Alder Cycloaddition

Another reaction that belongs to the class of pericylic reactions is the Diels Alder Cycloaddition. It was discovered by Otto Diels and Kurt Alder in 1928 and it refers to the bonding between the termini of a diene with a single saturated bond. With this in mind it is a π4s+π2s cycloaddition reaction, the 4π and 2π electrons coming from the diene and single saturated bond respectively. This totals 6 electrons involved, and as the reaction is thermally controlled, it therefore proceeds suprafacially with Hückel topology.

There are 2 possible transition states for the Diels Alder cycloaddition, called the exo and endo transition states. They give rise to two different isomeric products. The outcome of the reaction is dependent upon the relative stabilities of these two transition states. This is the aim of the experiement - to optimise and obtain structures for the relevant reactants and transitions states and to review the factors determining the relative stability of these structures.

Unsubstituted Reaction

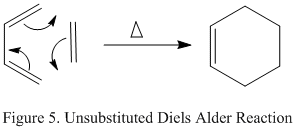
The unsubstituted reaction chosen for investigation in this experiment was the simplest one that occurs between cis-butadiene and ethylene. The reaction scheme for this is shown on the right in figure 5. The product of the reaction is cyclohexene.

Starting Materials

cis-butadiene

A molecule of cis-butadiene was drawn in Gaussview, and its geometry was optimised using the AM1 semi-empirical molecular orbital method. This method is used because it is a lower level of theory, and it must be used to ensure the molecule of cis-butadiene remains planar for the reaction. The planarity of the molecule is a prerequisite of a successful reaction, and any other level of theory will deform this. Its optimised structure is shown on the right and its HOMO and LUMO orbitals are presented below. The total energy of the molecule is 0.04878534 a.u. and its point group after symmetrising is C₂.

Optimised cis-butadiene

HOMO	LUMO
Orbital	Orbital

The HOMO of cis-butadiene is antisymmetric with respect to the plane running through the central bond and the LUMO is symmetric with respect to this plane. This is evident from the models shown above.

Ethylene

A molecule of ethylene was modelled in Gaussview and optimised using the AM1 semi-empirical level of theory in order to view its orbitals. The same method was use in order to be consistent with the study. Its optimised structure is shown on the right and its HOMO and LUMO orbitals are shown below. The total energy of the optimised ethylene molecule is 0.02619024 a.u. and its point group which was determined by symmetrising is D2h.

Optimised Ethylene

HOMO	LUMO
Orbital	Orbital

Upon observation of the important orbitals, HOMO and LUMO, it is clear to see that the HOMO is symmetric with respect to the plane that runs through the central bond. The LUMO however is antisymmetric in this respect.

For a reaction to be allowed there must be good orbital overlap between the contributing reactants. It is known that for good orbital overlap the contributing orbitals must present the same symmetrical properties and be of close enough distance that the densities can overlap. Using this theory, we can predict that the HOMO of cis-butadiene and the LUMO of ethylene will overlap a as they are both antisymmetric. Similarly the LUMO of cis-butadiene will overlap correctly with the HOMO of ethylene. These conditions mean this Diels Alder Cycloaddition will be allowed and the reaction can proceed.

Transition State

The structure of the transition state was estimated by drawing a bicylco molecule that would be obtained if cycohexadiene was used instead of cis-butadiene and then removing one -CH2-CH2- fragment so that an envelope transition state structure remained. This shape was chosen to ensure maximal overlap between the reactant orbitals. The intermolecular distance between the 2 reactant fragments in this structure was set to 2.2Å. This was to ensure it was not recognised as a C-C single bond by Gaussian during the optimisation. The transition state structure was optimised using the Hessian method, therefore the Job Type was changed to Opt+Freq, it was optimised to a transition state (TS Berny), the force constants were calculated once and the additional word, Opt=NoEigen, was included. The method used here was also the AM1 semi-empirical calculation.

The HOMO and LUMO of the transition state, post optimisation, are presented below.

HOMO	LUMO
Orbital	Orbital
Antisymmetric	Symmetric

The HOMO of the transition state is antisymmetric in nature and it can be seen to be made up from the overlap between the LUMO of ethene and the HOMO of cis-butadiene which are both antisymmetric with respect to the plane of the molecules. The LUMO of the transition state consists of overlap between the HOMO of ethene and the LUMO of cis-butadiene, which are both symmetric. As described above, the symmetrical nature of these contributions between the HOMO of one reactant and the LUMO of the other allow for good overlap and explain why the reaction is allowed. Overlap of these orbitals mean there is donation of electron density from the HOMO to the LUMO. It is important to note that if a different level of theory was used for these calculations, the structure and energy levels of these orbitals will be altered. It would be interesting to observe these differences.

Below in table 14 is a summary for the important parameters of the optimised transition state.

Table 14. Summary for Transition State - Unsubstituted Diels Alder Reaction

File Type	.chk
Calculation Type	FREQ
Calculation Method	RAM1
Basis Set	ZDO
Charge	0
Spin	Singlet
Total Energy	0.11165467 a.u.
RMS Gradient Norm	0.00002249 a.u.
Imaginary Frequency	-956.17cm-1
Dipole Moment	0.5605 Debeye
Point Group	Cs

There is an imaginary frequency at -956.17cm^-1 which proves the structure is one of a transition state. The animation for this particular vibration is shown above and corresponds to the movement of the reactants during the Diels Alder Cycloaddition.

It is evident from this animation that the formation of the two new δ_C-C bonds is synchronous. This differs from the lowest positive vibrational frequency of this transition state which occurs at -147.29cm^-1. The motion of this vibration is shown on the left and corresponds to an asynchronous bond formation between the 2 reactant molecules.

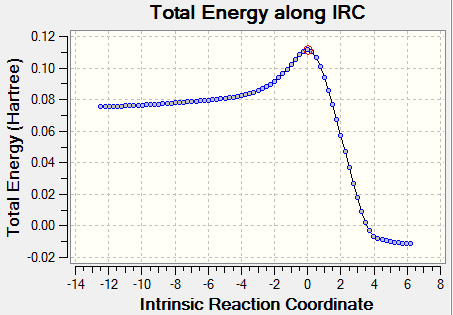
An intrinsic reaction coordinate (IRC) analysis was carried out on the transition state structure in both directions and using 50 steps along the reaction coordinate. The force constants were calculated always. This was to ensure the structure obtained for the optimised transition state was infact the maximum and to view the product of the reaction. The animation along with the IRC graph is shown below. The structure obtained for the transition state corresponds to the one at the top of the 'hill' with the red circle, and is therefore the transition state. The animation shown proves the bond making procedure in this process is synchronous.

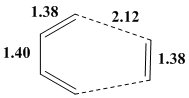
The image on the right shows the optimised bond lengths in the resultant transition state structure. Firstly the optimised intermolecular distance of 2.12Å is longer than a typical C-C bond length, 1.54Å, however is it shorter than the sum of the Van der Waals radius of each C atom, 3.40Å (1.70Å X2). This means they are close enough to exist within a bonding region which is expected as this is where the bonds are formed during the reaction. The other bond lengths in the molecule also correspond to a proceeding Diels Alder Cycloaddition. The double bonds in cis-butadiene and ethylene which were optimised to 1.38Å are longer than a typical C=C bond, 1.33Å, corresponding to the formation of single bonds which are present in the product. The same can be seen for the single bond in cis-butadiene, which has been optimised to 1.40Å. This length is shorter than a typical C-C single bond, 1.54Å, therefore this corresponds to the single altering to a double bond in the product.

Substituted Reaction

The unsubstituted Diels Alder Cycloaddition means that there is no particular regiospecificity as the reactants approach one another to form the transition state. However when the reactants bear substituents, there are available π orbitals that can interact with the structure, giving rise to regiochemistry. This means there are 2 available transition states for 2 different isomers - the endo and exo isomers. The reaction chosen for this study was the Diels Alder cycloaddition between cyclohexadiene and maleic anhydride. The reaction scheme is shown on the right in figure 6.

Starting Materials

Cyclohexadiene

A molecule of cyclohexadiene was modelled in Gaussview and was optimised using the HF/3-21G level of theory to a minimisation. Its optimised structure is shown on the right and its modelled HOMO and LUMO orbitals from the calculation are shown below. The total energy of the optimised molecule is -230.53967046 a.u. and after symmetrising the structure the point group is determined to be C_2v.

Optimised Cyclohexadiene

HOMO	LUMO
Orbital	Orbital

The images above show that the HOMO of cyclohexadiene is antisymmetric while the LUMO is symmetric with respect to the plane cutting through the molecule.

Maleic Anhydride

The second reagent, maleic anhydride, was drawn in Gaussview and optimised in Gaussian, again using the HF/3-21G level of theory to a minimisation. This is to ensure the method of calculations are kept constant in this particular study. The optimised structure is shown on the right and diagrams of the HOMO and LUMO are available below. The total energy of the optimised molecule us -375.10351335 a.u. and the point group determined after symmetrising is C_2v

Optimised Maleic Anhydride

HOMO	LUMO
Orbital	Orbital

The HOMO of maleic anhydride is symmetric with respect to the plane that slices the molecule through the central oxygen atom. The LUMO on the other hand is antisymmetric with this respect. This is evident from the models shown above. Due to the symmetrical properties of these orbitals, it is clear to see that there would be symmetrically allowed overlap between the HOMO of cyclohexadiene and the LUMO of maleic anhydride, and overlap between the LUMO of cyclohexadiene and the HOMO of maleic anhydride.

Transition States

There are 2 possible transition states possible for this reaction, determined by the orientation of the maleic anhydride molecule to the cyclohexadiene molecule. These are the exo and endo structures and both are studied in this experiment.

Exo

The structure of the exo transition state was estimated by drawing the exo isomer product and removing the bonds that are formed during the reaction. The distance between the reactants was set to 2.2Å in order that Gaussian did not recognise them as C-C bonds. The transition state structure was optimised using the Hessian method, therefore the Job Type was changed to Opt+Freq, it was optimised to a transition state (TS Berny), the force constants were calculated once and the additional word, Opt=NoEigen, was included. The method used for this calculation was the HF 3-21G level of theory.

HOMO	LUMO
Orbital	Orbital
Antisymmetric	Antisymmetric

Both the orbitals, HOMO and LUMO, of the exo transition state are antisymmetric with respect to the plane. With this in mind, it would be expected therefore that this consists of overlap from the HOMO of cyclohexadiene and the LUMO of maleic anhydride, as they are both antisymmetric. Observation of the models above support this theory as the shapes of the orbitals matches very closely to the optimised reactant orbitals presented in the previous section. In the HOMO it is evident that the electron density surrounding the C=O fragments is of the correct phase to interact with the diene orbitals. However this does not occur due to large distance between these two groups, therefore there is no stabilising secondary orbital overlap here.

An intrinsic reaction coordinate analysis was carried out on the obtained exo transition state to ensure the structure obtained was a maximum on this plot, and therefore definitely a transition state. It was also run to ensure that the product was definitely the exo isomer. The reaction coordinate plot and an animation showing the process involved in this coordinate is shown below. The calculation was run in both directions and using 50 steps along the reaction coordinate. The force constants were calculated always.

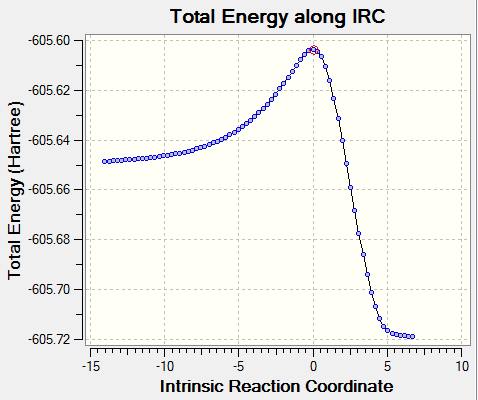
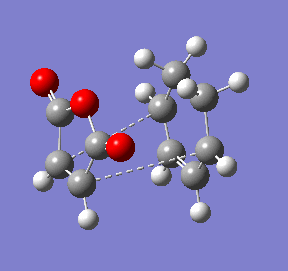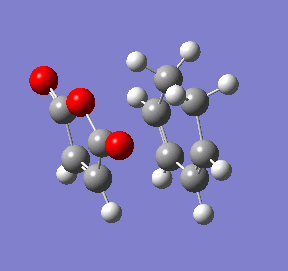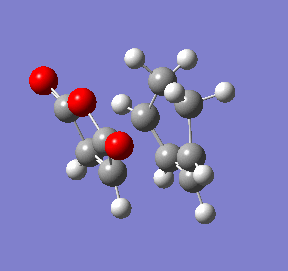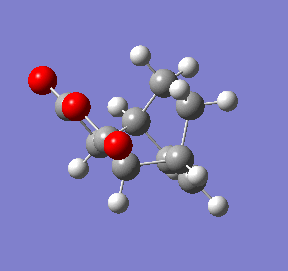
The point at the top of the reaction coordinate plot (red circle) is indeed the structure obtained from optimisation of the transition state guess structure. Addtionally the animation proves that the exo isomer is the desired product from this transition state. This product lies to the right of the maximum in the reaction coordinate plot, at the minimum. The animation also shows the concerted nature of the bond formation during the reaction.



Table 15 shows the important information obtained from the optimisation of the exo transition state. Its point group C₁ was determined after symmetrising the molecule.

Table 15. Summary for Exo Transition State

File Type	.chk
Calculation Type	FREQ
Calculation Method	RHF
Basis Set	3-21G
Charge	0
Spin	Singlet
Total Energy	-605.60359114 a.u./ -380022.07209818 kcal/mol
RMS Gradient Norm	0.00003892 a.u.
Imaginary Frequency	-647.87cm-1
Dipole Moment	5.9369 Debeye
Point Group	C1

There is an imaginary frequency, as expected for a transition state, at -647.87cm^-1. This is further conformation that the structure is transition state in nature. The animation for this particular vibration is also shown above and corresponds evidently to the concerted pericylic reaction that is the Diels Alder Cycloaddition.

The illustration shown on the right shows the important bond lengths in the optimised molecule. The measurements can confirm the progression of the reaction. Firstly the H₂C-CH₂ has been optimised to 1.56Å which is close to the typical C-C (sp³)(1.54Å) bond length which is the correct form of this bond in the product. The double bonds in the cyclohexadiene and malec anhydride reactants have both been optimised to 1.37Å. These lengths are longer than a typical C=C (sp²)bond as during the reaction they become single C-C bonds. The single bond that is present in between the 2 double bonds in cyclohexadiene, which is the only C=C bond present in the product is optmised to 1.40Å, which as expected is shorter than the typical C-C (sp³) bond length (1.54Å) and is closer to the length of a typical C=C (sp²) bond (1.33Å). The distance between the 2 fragments is 2.26Å.

The distance between the -(C=O)-O-(C=O)- fragment of the maleic anhydride and the carbons from the H₂C-CH₂ bridgehead is 3.19Å.

Endo

Similary to the exo transition state, the endo transition state was estimated and modelled by drawing the endo isomer product of the Diels Alder reaction and removing the 2 δ_C-C bonds that are formed during the reaction. The distance was again set to 2.2Å between the reacting centres of the 2 reactants. The difference between this isomer and the exo isomer is that the maleic anhydride is orientated by 180°. The endo transition state guess structure was optimised using the Hessian method, therefore the Job Type was changed to Opt+Freq, it was optimised to a transition state (TS Berny), the force constants were calculated once and the additional word, Opt=NoEigen, was included. The method used for this calculation was the HF 3-21G level of theory.

HOMO	LUMO
Orbital	Orbital
Antisymmetric	Antisymmetric

Again upon observation of the models above, it can be seen that both the HOMO and LUMO of the endo transition state are antisymmetric with respect to the plane. It can also be seen that they are made up of the HOMO of cyclohexadiene and the LUMO of maleic anhydride due to the close match in the shapes of the orbitals. This is as expected cos this match of orbitals brings two antisymmetric orbitals together, resulting in an allowed reaction. Here there is secondary orbital overlap occuring. In the HOMO (see above) the orbitals on the carbonyl fragments from the maleic anhydride have the correct phase for overlap with the olefin H₂C=CH₂ orbitals. This is the same for the exo isomer, however due to the orientation of the maleic anhydride in the endo transition state, they groups of orbitals are close enough to interact.

An intrinsic reaction coordinate analysis was carried out on the obtained endo transition state to ensure the structure obtained was a maximum on this plot, and therefore definitely a transition state. It was also run to ensure that the product was definitely the endo isomer. The reaction coordinate plot and an animation showing the process involved in this coordinate is shown below. The calculation was run in both directions and using 50 steps along the reaction coordinate. The force constants were calculated always.

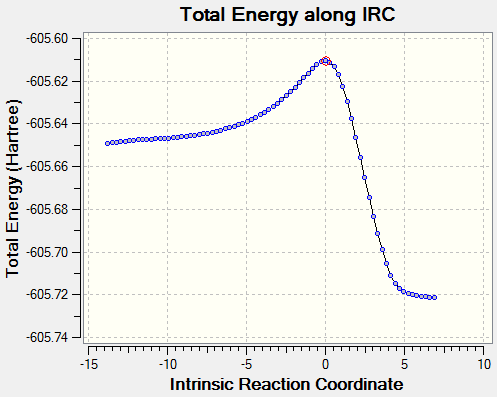
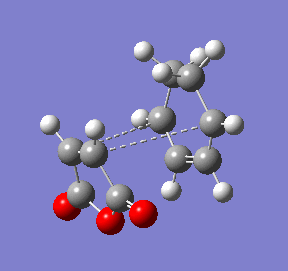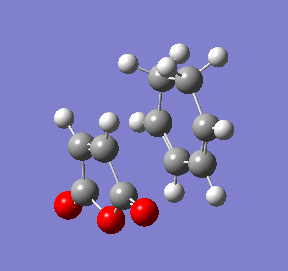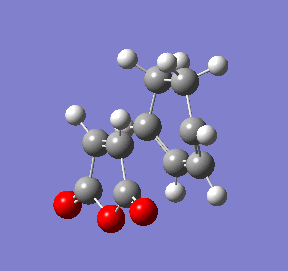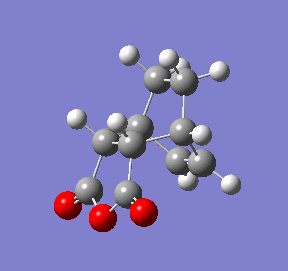
Once again a transition state has definitely been obtained as its structure corresponds to the point right at the maximum of the reaction coordinate plot (red circle). The animation of this coordinate presents the concerted formation of the 2 δ_C-C bonds during the reaction and also confirms the desired endo isomer as the product. Interestingly, the reaction coordinate plot also shows the product for the endo transition state is higher in energy than that of the exo transition state.


Table 16 below presents the optimisation results of the endo transition state structure. The point group, determined after symmetrising, is C_s.

Table 16. Summary for Endo Transition State

File Type	.chk
Calculation Type	FREQ
Calculation Method	RHF
Basis Set	3-21G
Charge	0
Spin	Singlet
Total Energy	-605.61036821 a.u./ -380026.32477472 kcal/mol
RMS Gradient Norm	0.00001343 a.u.
Imaginary Frequency	-643.73cm-1
Dipole Moment	6.7148 Debeye
Point Group	Cs

The imaginary frequency evaluated at -643.73cm^-1 proves the structure lies at a maximum on the PES confirming that it is indeed a transition state. The animation shows this vibration in motion and corresponds to the concerted Diels Alder Cycloaddition.

The illustration shown on the right indicates the important bond lengths in the optimised molecule. It indicates progression of the particular reaction. The double C=C bonds in the cyclohexadiene and the maleic anhydride are optimised to the bond length of 1.37Å in the transition state. This indicates progression as these lengths are longer than the typical C=C (sp²), 1.33Å, and mean they are becoming C-C single bonds. The H₂C-CH₂ bridgehead has been optimised to a length of 1.56Å which is extremely close to the typical C-C (sp³), 1.54Å. The is as expected as the bond is a C-C single bond in the product. The position of the only double bond in the product has been optimised to 1.40Å, which is lower than the typical C-C (sp³) bond length, 1.54Å, and lies closer to the typical C=C (sp²) length, 1.33Å. This confirms the process of reaction. The distance between the 2 fragments in the endo transition state is calculated to be 2.23Å

The distance between the -(C=O)-O-(C=O)- fragment of the maleic anhydride and the carbons from the HC=CH olefin group is 3.10Å. This length and the distance between the 2 fragments that make up the transition state are the only ones that differ between the 2 transition state conformers.

Activation Energy

The data to calculate activation energies was obtained from frequency analyses of the exo and endo transition states, along with the frequency analysis of the starting materials, cyclohexadiene and maleic anhydride. The sum of the energies of the reactants was calculated and the difference between this value and the transition states yielded the activation energies. The calculations were carried out at both levels of theory, HF/3-21G and B3LYP/6-31G*.

Table 16. Activation Energies - Substituted Diels Alder (kcal/mol)

	Hartree Fock Method		B3LYP/6-31G* Method
	0 K	298.15 K	0 K	298.15 K
Exo Transition State	26.65218976	26.87872051	18.10928223	18.46821738
Endo Transition State	22.40771888	22.61228682	15.51767006	15.87848774

From the data it is clear that the activation energy leading up to the endo transition state is lower than for the exo transition state. This means this reaction pathway is more favourable and that the endo isomer is kinetically favoured over the exo isomer.

Endo vs. Exo Summary

From the IRC data shown for each transition state, it shows that in fact the exo isomer product is in lower in energy than the endo isomer product. The transition state for the endo isomer however is lower in energy than for that of the exo transition state, this is proved by the activation energy calculations shown above. Despite the energy differences between the isomeric products, the endo is favoured over the exo isomer which proves the reaction is under kinetic control.

The stability of the endo transition state is evidently due to secondary orbital overlap. This occurs between the C=O orbitals which are in close proximity with the olefin orbitals of the cyclohexadiene fragment. They have the same symmetry properties, allowing good orbital overlap. The overlap is also represented by the distance between the 2 fragments in the transition state, where the orbital overlap occurs in the endo transition state, this length is shorter at 2.23Å. From the bond length analysis carried out, it is clear to see that the -(C=O)-O-(C=O)- fragment of the maleic anhydride lies closer to the HC=CH olefin group in the endo transition state. Oppositely the -(C=O)-O-(C=O)- fragment of the maleic anhydride in the exo form is closer to the H₂C-CH₂ bridgehead. The exo transition state therefore would experience some strain due to the proximity to this bulky H₂C-CH₂ bridgehead, also explaining its higher energy.

Conclusion

The substituted Diels Alder Cycloaddition has been studied vigorously in terms of its reactants and transition states. Optimisations have been carried out to obtain preliminary structures which have had analysis carried out upon them, in the form of IRCs, bond lengths and energies. It has been confirmed that the correct structures have been obtained as they lead to the desired products. Conclusively, the endo transition state is lower in energy and therefore more stable than the exo transition state. This can be explained by secondary orbital overlap which was evaluated by observation of the frontier molecular orbitals responsible.

A factor that has been neglected throughout this study is deviations from standard conditions that these calculations were carried out in, for example in real laboratory conditions. The main differences would be in solvents, temperature and pressure. It would be useful to investigate these differences to observe the solvent, temperature and pressure effects. Another factor that was somewhat treated superficially during these experiments were the use of different levels of theory. Although most were covered and utilised, it would be interesting to compare them directly.