Rep:Mod:PWPH14
COMPUTATIONAL LABS: PHYSICAL
The Cope Rearrangement
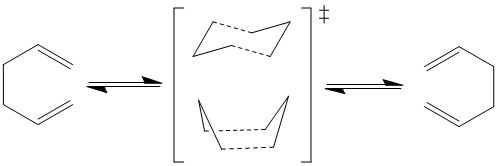
The Cope rearrangement, developed by Arthur C. Cope in 1940, is a [3,3] sigmatopic rearrangement of 1,5 dienes that consists of the migration of an allyl fragment[1]. It was initially unclear whether this reaction proceeded via a concerted or a diradical mechanism. Only in 1994, more than fifty years later, the development of computational techniques allowed analysis of energy minimas and transition states proving that the reaction as a concerted mechanism via either a chair or a boat transition states[2]. Following the Woodward-Hoffman selection rules, the overall reaction involves 6 electrons (4n+2) and suprafacial components making it a thermally allowed reaction with retention of configuration at the migrating centre.
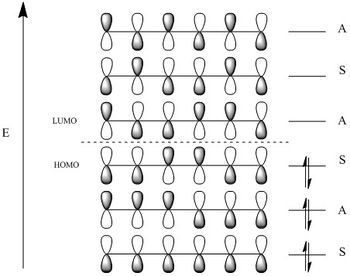
Figure 1 above shows 1,5-hexadiene undergoing the Cope Rearrangement and the two possible TS, and figure 2 shows the orbitals of 1,5-hexadiene, where the HOMO MOs can be seen with suprafacial topology.
In this computational experiment GaussView 5.0. is used to create, optimise and analyse the energy maxima and energy minima of the reaction shown above. Different methods and Basis Sets are used to obtain higher level of accuracy or faster calculation times.
1,5 Hexadiene conformers
The lowest energy conformers of 1,5-hexadiene have an antiperiplanar or gauche relation between the four central carbons. Both were modeled and optimised using the Hartree-Fock method and a split valence Basis set 3-21G.
The results have been summarised in the table below. The total energies and symmetries of the different conformers are shown as well as the relative energies between them. In all, gauche3 conformer as the lowest energy configuration and the anti3 as the highest energy conformer.
| Antiperiplanar configuration | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
| |||||||||
| anti3 | anti1 | anti2 | |||||||||
| -231.689071 a.u. | -231.692602 a.u. | -231.692535 a.u. | |||||||||
| Relative energy (kcal/mol) = 2.253 | Relative energy (kcal/mol) = 0.037 | Relative energy (kcal/mol) = 0.079 | |||||||||
| C2h | C2 | Ci | |||||||||
| Optimisation log file | Optimisation log file | Optimisation log file | |||||||||
| Optimisation summary | Optimisation summary | Optimisation summary | |||||||||
| Gauche configuration | |||||||||||
|
|
| |||||||||
| gauche3 | gauche2 | gauche5 | |||||||||
| -231.692661 a.u. | -231.691667 a.u. | -231.689616 a.u. | |||||||||
| Relative energy (kcal/mol) = 0.000 | Relative energy (kcal/mol) = 0.624 | Relative energy (kcal/mol) = 1.911 | |||||||||
| C1 | C2 | C1 | |||||||||
| Optimisation log file | Optimisation log file | Optimisation log file | |||||||||
| Optimisation summary | Optimisation summary | Optimisation summary | |||||||||
To explain the relative stability of the different conformers, two different stabilising effects are taken into account:
- Favorable overlap between σ/σ* orbitals in antiperiplanar arrangements
- Attractive Van der Waals interactions between Hydrogen atoms that arise from gauche arrangements known as the gauche effect
σ/σ* orbital interaction is usually the dominant effect and so usually the antiperiplanar arrangement dominates. However, as alkane chains get larger, favorable Van der Waals interactions appear between H atoms in chains with gauche configuration (i.e. bent chains not linear). The distance between these H atoms is around 2.41Å and it can be seen in the table above.
For gauche3, it is clear how both interactions between H atoms are at optimum distance and are therefore favorable stabilising the overall energy. Gauche2 only has one Van der Waals interaction making it less stable than gauche 3, and finally gauche 5 (although it also has a Van der Waals interaction) is much more unstable due to the strong repulsion between the two H atoms at a distance of 2.23Å.
As for the antiperiplanar conformers, anti3 is the highest energy conforation of all due to the fact that although it has antiperiplanar arrangement at the central four carbons, there is an eclipsed formation between the first four carbons and the last four carbons. Eclipse conformation is the highest in energy due to the strong repulsion between bonds, and it is very rarely adopted. As for anti 1 and anti 2 conformers, very simmilar in energy between themselves and even between the gauche2 conformer. The reason for this is the "inwards" angle that they form that can also lead to H bonding and therefore overall stabilisation.
3-21G and 6-31G* basis sets
With the following exercise, two different basis set are used to optimise the geometry of the anti2 conformer drawn before. The Optimisation calculation consists in solving the Schrodinger equation for different positions of the atoms and finding the one that has the lowest energy. In order to define the molecular orbitals of the atoms, linear combination of basis functions are used as an approximation. The higher number of basis functions used will make the optimisation more accurate. 3-21G is a lower basis set than 6-31G, therefore the results of the optimisation are expected to be more accurate. It is very important to note that the optimised energies of different basis sets cannot be compared as the energy has been calculated using completely different functions. However, using the same basis set and the same method, conformers can be conpared and transition states calculated.
The results of the optimisation are shown below.
| 3-21G basis set | 6-31G(d) basis set | |
|---|---|---|
| Total Electronic Energy | -231.692535 a.u. | -234.611703 a.u. |
| Symmetry | Ci | Ci |
| Optimisation Log file | Opt 3-21G | Opt 6-31G (d) |
| Optimisation summary | Opt Summary 3-21G | Opt Summary 6-31G (d) |
| Frequency Log file | Freq 3-21G | Freq 6-31G (d) |
| Sum of electronic and zero-point energies | -231.539539 a.u. | -234.469212 a.u. |
| Sum of electronic and thermal energies | -231.532565 a.u. | -234.461856 a.u. |
| Sum of electronic and thermal enthalpies | -231.531621 a.u. | -234.460912 a.u. |
| Sum of electronic and thermal free energies | -231.570916 a.u. | -234.500821 a.u. |
| Entropy | 82.703 cal/molK | 83.997 cal/molK |
| Thermal Energy | 100.383 Kcal/mol | 94.030 Kcal/mol |
Both 3-21G and 6-31G show very similar structures and the same symmetry label. There are, however, differences in the bond angles and bond lengths. These differences can be seen in the table below.
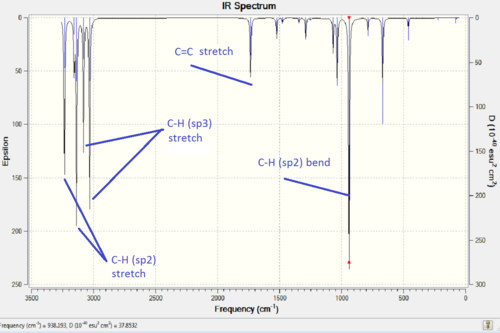
A frequency calculation was also carried out. No negative vibrations indicates a successful optimisation as it shows that the stationary point found is a minima (a maxima would be a transition state and would indeed show a negative vibration frequency), the IR spectra is shown above with the most important bending and stretching vibrations.
Also included in the table above is basic thermochemical data: the Potential Energy at 0K (Sum of electronic and zero-point energies) and at 298.15 K (Sum of electronic and thermal energies), the Sum of electronic and thermal enthalpies (includes a correction for RT) and the sum of electronic and thermal free energies (includes the entropic contribution to the free energy).
| angle
C1-C2-C3 |
angle
C2-C3-C4 |
dihedral
C2-C3-C4-C5 |
dihedral
C1-C2-C3-C4 |
bond distance
C1-C2 |
bond distance
C2-C3 |
bond distance
C3-C4 | |
|---|---|---|---|---|---|---|---|
| 3-21G basis set | 124.81° | 111.35° | 180.00° | 114.70° | 1.316 Å | 1.509 Å | 1.553 Å |
| 6-31G(d) basis set | 125.29° | 112.67° | 180.00° | 118.53° | 1.334 Å | 1.504 Å | 1.548 Å |
Optimizing Boat and Chair Transition Structures
| Hessian Optimisation | Frozen Coordinates Optimisation | |
|---|---|---|
| Total Electronic Energy | -231.6193 a.u. | -231.6193 a.u. |
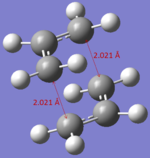
| Distance of bond formation/cleavage | 2.021 Å | 2.021 Å |
| Optimisation Log file | Hessian Opt | Frozen Coord Opt |
Transition States can also be calculated and optimised using computational techniques. The Cope rearrangement TS can be found using various methods:
- Hessian Optimisation
- Frozen Coordinates Optimisation
- QST2 Optimisation
The Chair TS was Optimised using both the Hessian and the Frozen Coordinates method, and the Boat TS was optimised with the QST2 method.
Chair TS (C2h)
To draw the Chair transition state, an allyl fragment was created and optimised using HF/3-21G method. Summary here, log file here.
Then two allyl fragments were situated in a chair like position fixing the distance between the terminal atoms to 2.2 Å. The transition state was optimised and the results are summarised in the table below. The main advantage of this method is its simplicity as it only involves one step, but the main disadvantage is that the structure optimised must be very simmilar to the transition state (which in this case is not complicated as only small fragments are being dealt with).
Another optimisation method used was the Frozen coordinates method which involves two steps: first the coordinates of the atoms involved in formation/cleavage of bonds are all fixed for a first optimisation of the rest of the structure and second, the atoms are un-fixed and another optimisation is carried out. The main advantage for this method is that although it involves 2 steps, by fixing the position of certain atoms, long calculations can be avoided when optimising complicated transition state structures.
The parameters of the optimisations used were the following:
- method: HF
- Basis set: 3-21G
- Calculation: Opt+Freq
- Opt to a TS (Berny)
- Force constants calculated once (not for frozen coordinates)
- Additional keywords: Opt=NoEigen
The results obtained with either method are exactly the same.
The optiised structure of the chair transition state has a bond distance between the forming/cleaving atoms of 2.021 Å and the same energy (the basis set and the method used for optimisation of the structures is the same, therefore they can be compared and expected to be equal).
The frequency analysis carried out can also show that the transitions state optimisation was successful by showing a negative vibration frequency (imaginary frequency) a around -817 cm-1 that corresponds to the sigma bond vibration (seen in the small animation.
Boat TS (C2v)
For the Boat Transition state an entirely different method was used. The QST2 method finds the optimised transition state from the optimised structures of the reactant and the product. Because the chair TS is lower in energy than the boat TS, the first optimisation was unsuccessful. The structure of the reactant and the product was then changed by modifying the dihedral andgle from 180° to 0° and the angle between the internal C-C-C angles to 100°. the structure of the reactant and the product was changed to this which made it possible to find the boat TS using the following optimisation parameters (same as before):
- HF, 3-21G basis set
- Calculation: Opt+Freq
- Opt to a TS (QST2)
- Force constants calculated never
An imaginary frequency was also found showing again a successful optimisation. This vibration mode and be seen on the left of the page and is at about -840 cm-1. The reason why this vibration frequency is much lower than in the chair conformation is because of the direct relation of the energy of these transition states. The boat TS has stronger interactions between the bond forming/breaking atoms because it is less stable than the chair TS which give rise to a more negative imaginary vibration
IRC analysis of Boat and Chair conformers
From the Chair and the Boat Transition state optimisations, the reaction path can be followed by calculating the IRC (Intrinsic Reaction Path). Starting from the Transition State, the calculation can be done forward or backwards to reach the product or the reactant respectively. It is another way (besides the imaginary vibration) of checking whether or not the transition State has actually been found and to find out what conformation will the product present.
Both for the chair and the boat TS, the IRC was calculated from the Hessian HF/3-21G optimised structure. When the appropriate energy minima is found it is optimised to the same method/basis set to generate the product. The local energy minima found initially has a similar energy but not equal to the desired product, this is why it is further optimised to reach the actual minima and the wanted product.
The calculation was only set up forward and the force constants were calculated at each data point. The results are sumarised below.
In all, the chair TS needed 44 steps to find a local energy minima and the boat needed 75 steps. When the final step was found, they were both optimised again to HF/3-21G to give the predicted product. In the case of the chair TS, the product was clearly gauche2 firstly because the energies calculated from the first exercise where the same and the structure of the molecule was very similar too. As for the boat structure, the results suggest that perhaps the optimisation was not as successful as expected, although the energy of the reported minima did not match the expected gauche/anti conformers, the structure of the predicted product is very similar to Gauche3. This might be because the structure adopted by the product is not strictly a gauche or a antiperiplanar conformer (different dihedral angle or internal angles) or more likely, because the optimisation basis set is not large enough and the accuracy is not ideal.
| IRC Graph | Local energy minimum
(Point) |
Local energy minimum
(Energy) |
IRC Log file | Optimised Energy minimum | Optimised Energy minimum
(Energy) |
Optimisation Log file | Conformer |
|---|---|---|---|---|---|---|---|
| Chair | 44 | -231.691579 a.u. | here | 
|
-231.691667 a.u. | here | Gauche2 |
| Boat | 75 | -231.695243 a.u. | here | 
|
-231.695275 a.u. | here | ≈ Gauche3 |
Activation Energy
The table below collects the most important data obtained from the optimisation of the TS.
Both optimised transition states for the cope rearrangement were optimised to a higher level of theory: B3LYP/6-31G(d) and their frequency calculations were also run in order to know the Activation Energies of the reaction. As expected, the activation energy was lower at a higher temperature. The values predicted by the literature that assigned ΔE=33.5 ± 0.5 kcal/mol (at T=0 K) for the reaction via the chair TS and ΔE=44.7 ± 2.0 kcal/mol (at T=0 K) for the reaction via the boat TS. The higher level theory method predicts an activation energy closer to the experimental value.
As mentioned before in the first section, the Chair transition state is the lowest energy TS. The activation energy (Energy of TS - Energy of SP) will be lower for the Chair TS than for the boat TS. Both transition states have negative vibration frequencies and the starting material does not, which indicates correct optimisation calculations.
For the negative frequencies, we find that they parallel the trend set by the distance between the fragments. So, when an average basis set is used, we find that (as mentioned before) shorter distances mean higher interactions therefore "more" negative frequencies (which is what happens with the chair conformation). However when the higher (better and more accurate) basis set is used, we find that the transition state with the shortest distance between the fragments and therefore "more" negative frequencies is the chair TS. A reasonable explanation for this could be that a higher method and basis set was used, taking into account more orbitals and being more accurate, perhaps including aromatic characteristics only for the chair transition that would make the interactions much stronger.
|
|
| |
| B3LYP/6-31G(d) | Starting Product | Boat TS | Chair TS |
|---|---|---|---|
| Log File | here | here | here |
| Total Electronic Energy | -234.611703 a.u. | -234.543091 a.u. | -234.556983 a.u. |
| Distance between fragments | - | 2.208 Å | 1.967 Å |
| Imaginary Frequency | - | -530.15 cm-1 | -565.56 cm-1 |
| Sum of Electronic and ZPE (at 0 K) | -234.469212 a.u. | -234.402314 a.u. | -234.414924 a.u. |
| Sum of Electronic and Thermal energies
(at 298.15 K) |
-234.461856 a.u. | -234.395962 a.u. | -234.409003 a.u. |
| Activation Energy at 0 K (ΔE) | - | 41.98 Kcal/mol | 34.07 Kcal/mol |
| Activation Energy at 298.15 K (ΔE) | - | 41.35 Kcal/mol | 33.17 Kcal/mol |
| HF/3-21G Basis Set | Starting Product | Boat TS | Chair TS |
| Total Electronic Energy | -231.692535 a.u. | -231.602802 a.u. | -231.619322 a.u. |
| Distance between fragments | - | 2.140 Å | 2.021 Å |
| Imaginary Frequency | - | -840.05 cm-1 | -817.92 cm-1 |
| Sum of Electronic and ZPE (at 0 K) | -231.539539 a.u. | -231.450927 a.u. | -231.466702 a.u. |
| Sum of Electronic and Thermal energies
(at 298.15 K) |
-231.532565 a.u. | -231.445298 a.u. | -231.461343 a.u. |
| Activation Energy at 0 K (ΔE) | - | 55.60 Kcal/mol | 45.71 Kcal/mol |
| Activation Energy at 298.15 K (ΔE) | - | 54.76 Kcal/mol | 44.69 Kcal/mol |
References
- ↑ J. Am. Chem. Soc., 1940, 62 , 441 DOI:10.1021/ja01859a055
- ↑ J. Am. Chem. Soc., 1994, 116, 1072 DOI:10.1021/ja00082a032
Diels Alder Cyclo-Addition
Ethylene and Cis-butadiene cyclo-addition
With the computational techniques used before during the report, the following pericyclic cycloaddition was analysed. First, the starting materials were Optimised and a Frequency Analysis was carried out, and then the transition states were predicted. The semi-empirical theory level AM1 was used throughout the exercise to be able to compare the energies and HOMO LUMO MOs. For the transition state, the HESSIAN method was used.
Geometry analysis, Activation energy and HOMO/LUMO molecular orbitals were calculated and discussed at the end of this section.
Starting materials
Ethylene
One of the starting products was drawn, Optimised and a Frequency analysis carried out. The files and the symmetry of the HOMO/LUMO molecular orbitals can be seen below.
| HOMO | LUMO | ||||||
|---|---|---|---|---|---|---|---|
|
| ||||||
| along vertical plane: symmetric | along vertical plane: anti-symmetric |
Cis-Butadiene
The same calculations was carried out for cis-butadiene (the other starting product), and again the results can be seen together with he symmetry of the frontier MOs.
| HOMO | LUMO | ||||||
|---|---|---|---|---|---|---|---|
|
| ||||||
| along vertical plane: anti-symmetric | along vertical plane: symmetric |
Transition state optimisation
The prediction of the transition state was carried out using Hessian instead of QST2. Results shown below.
- method: semi-empirical AM1
- Calculation: Opt+freq
- Log file here HESSIAN
- Negative Vibration at -818.26 cm-1
- Total energy: 0.11165467 a.u.
| HOMO | LUMO | ||||||
|---|---|---|---|---|---|---|---|
|
| ||||||
| along vertical plane: anti-symmetric | along vertical plane: symmetric |
Discussion
The molecular orbitals of the transition state can be predicted by combining the MO of same symmetry of the starting products:
- HOMO (TS) = LUMO (ethylene) + HOMO (cis-butadiene), (both a)
- LUMO (TS) = HOMO (ethylene) + LUMO (cis-butadiene), (both s)
The HOMO MO of the TS is shown in the image below. Similarly, the LUMO MO of the TS could have been sketched.
From the sketch it can be seen how the reaction is suprafacial (occurs all in the same face) and synchronous. 6 electrons (4n+2) are involved in this concerted mechanism that according to Woodward-Hoffman will be thermally allowed.

As seen in the previous exercises, the activation energy of the reaction can be calculated from the Thermochemical data found from the fraquency analysis file. The energy of the starting materials will be the sum of both energies of the separate products. The following table summarises the calculations.
| Starting Molecules | Transition state | |||
|---|---|---|---|---|
| Cis-butadiene | Ethylene | Total | ||
| Total Electronic Energy | 0.048797 a.u. | 0.026190 a.u. | 0.074987 a.u. | 0.111655 a.u. |
| Sum of electronic and zero-point energies | 0.134552 a.u. | 0.077201 a.u. | 0.211753 a.u. | 0.253275 a.u. |
| Sum of electronic and thermal energies | 0.138573 a.u. | 0.080255 a.u. | 0.218828 a.u. | 0.259452 a.u. |
| Activation Energy at 0 K (ΔE) | 26.06 Kcal/mol | |||
| Activation Energy at 298.15 K (ΔE) | 25.49 Kcal/mol | |||
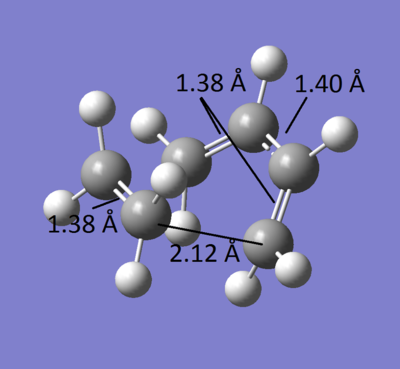
As for the geometry of the TS, the image below shows the C-C distances in the molecule. Knowing that C(sp3 bond length)= 1.54 Å, C(sp2 bond length)= 1.34 Å and C(sp bond length)= 1.19 Å, we can see that all the bonds that correspond to the "old" fragment bonds are all around 1.38 Å, which is longer than the usual double bond but much shorter than a single bond. Both Bonds that are about to form are 2.12 Å, longer than the expected single bond so no bond is formed yet. No bond is actually expected to appear, the TS corresponds to the energy maxima and the molecule cannot stay in this state.
The Van der Waals radii of C is 1.7 Å, which means that favorable interactions between C can be found between C atoms at about 3.4 Å apart. No Van der Waals interactions occur withing the TS: All C-C bonds are too short for Van der Waals, and H atoms are too far apart to form favorable interactions.
Cyclohexa-1,3-diene and Maleic Anhydride cyclo-addition
As in the concerted reaction before, the cyclo-addition can be analysed using computational techniques. The same structure as before is followed: first optimisation and frequency analysis of the starting products using the semi-empirical AM1 method is carried out, and then the transition structures is predicted, this times using the QST2 optimisation.
Starting materials
maleic anhydride
| HOMO | LUMO | ||||||
|---|---|---|---|---|---|---|---|
|
| ||||||
| along vertical plane: symmetric | along vertical plane: anti-symmetric |
Cyclohexa-1,3-diene
| HOMO | LUMO | ||||||
|---|---|---|---|---|---|---|---|
|
| ||||||
| along vertical plane: anti-symmetric | along vertical plane: symmetric |
Endo and Exo Transition States
EXO
- method: semi-empirical AM1
- Calculation: Opt+freq
- Log file here QST2
- Summary here here
- Imaginary vibration: -812.16 cm-1
- Energy: -0.050420
| HOMO | LUMO | ||||||
|---|---|---|---|---|---|---|---|
|
| ||||||
| anti-symmetric | symmetric |
ENDO
- method: semi-empirical AM1
- Calculation: Opt+freq
- Log file here QST2
- Summary here here
- Imaginary vibration: -806.45 cm-1
- Energy: -0.051505 a.u.
| HOMO | LUMO | ||||||
|---|---|---|---|---|---|---|---|
|
| ||||||
| anti-symmetric | symmetric |
Discusion

Unlike the previous reaction, where only one transition state existed, in the Diels alder-reaction two different transition states exist depending on the direction that both MOs interact. The reaction examined is known as a concerted cyclo-addition between a conjugated electron rich diene and a dienophile, so depending whether the dienophile is oriented towards the diene π system or it is oriented away from it there will be two possible probducts with different configurations. Substituents on the dienophile or electron donating groups on the diene can promote one transition state or another depending on the MO combinations. For usual starting materials with "normal demand" of Diels Alder (Diene has a higher energy HOMO than dienophile HOMO) the endo transition state is usually preferred. The reason for this is because although it can be usually more sterically hindered, there is a better interaction between the π bond of substituents on the electron poor dienophoile and the conjugated diene (secondary orbital overlap). Van der Waals interaction can also be key in changing the predicted endo:exo ratio. Not only due to interactions withing the molecule but with the solvent that can stabilise a certain TS and favor the unexpected product.
| Starting Molecules | Transition state | ||||
|---|---|---|---|---|---|
| Maleic anhydride | 1,3-Cyclohexadiene | Total | Endo | Exo | |
| Total Electronic Energy | -0.121824 a.u. | 0.027711 a.u. | -0.094113 a.u. | -0.051505 a.u. | -0.050420 a.u. |
| Sum of electronic and zero-point energies | -0.063346 a.u. | 0.152502 a.u. | 0.089156 a.u. | 0.133496 a.u. | 0.134880 a.u. |
| Sum of electronic and thermal energies | -0.058192 a.u. | 0.157726 a.u. | 0.099534 a.u. | 0.143685 a.u. | 0.144881 a.u. |
| Activation Energy ENDO | 27.82 Kcal/mol (T= 0 K)
27.71 Kcal/mol (T= 298.15 K) | ||||
| Activation Energy EXO | 28.69 Kcal/mol (T= 0 K)
28.46 Kcal/mol (T= 298.15 K) | ||||
In the table shown above Endo has overal a lower electronic energy than the exo transition state and a lower activation energy which would usually determine that it would be the major product.
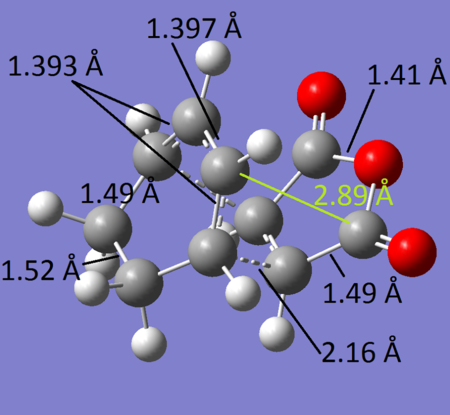

Above, the structural features of each transition states can be seen. It's very interesting to note that although the approach is entirely different, the bonds formed/broken/modified are still the same. The only major change is the interatomic distance between the bridging C atom and the carbonyl carbon opposite itself. The difference is quite large:
- C-C(EXO distance)= 2.95 Å
- C-C (ENDO distance)= 2.89 Å
As mentioned before, the endo appears to be more sterically hindered (C Van der Waal radii = 1.7 Å, so no interatomic distances that could result in favorable interactions), but it is unexpectedly the lowest energy conformer. By analysing the HOMO MO again of the Endo TS and the Exo TS we can see the secondary orbital interactions mentioned before: the (O=C)=CO=(C=O)has MO on the terminal O atoms that can overlap with the diene conjugated π system. This rearrangement is only existent when the TS is endo, as the π system is directly above the O. In the Exo structure however, the Conjugated π system and the secondary orbitals on the O are in opposite sides of the molecule so no interaction happen.
What effects have been neglected in these calculations of Diels Alder transition states?
Computational techniques used in this exercises have been assumed to be gas phase with no solvent. It has not taken into account temperature other than 0K and 298.15K and pressure at 1atm. However, pericyclic reactions a very susceptible to steric pressure that will force them to undergo the reactions via a certain TS. Therefore higher pressure or lower volume could be investigated in more depth. Solvent effects (as mentioned before) can also change the outcome of the reaction due to H-bonding that could lower the relative energy of a transition state. There is a relatively small solvent effect on the rate of reaction (unless the reactants are charged) but the H-bonds formed are definetely key when undergoing diels alder reactions in protic solvents like water.