Rep:Mod:PS4615
Introduction to Molecular Modelling 2
NH3 Optimization
General Data
In this first session, NH3 (ammonia) molecule is optimized using the following method:
Calculation Method : RB3LYP
Basis Set : 6-31G(d,p)
Type of Calculation : OPTF (optimise and frequency analysis)
The information below are the data obtained from the optimization of the NH3 molecule using the method mentioned above:
Final Energy E(RB3LYP) in atomic units (au) : -56.55776873 a.u
RMS Gradient Norm : 0.00000485 a.u
Point Group of NH3 : C3V
And the following are the bond data obtained:
N-H bong length : 1.01798 Å (same for the three N-H bonds)
H-N-H bond angle : 105.741°
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Predicted change in Energy=-5.986284D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7412 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7412 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7412 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.8571 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
The attached data above confirmed that the structure converged, hence it is optimized to an acceptable degree.
NH3 molecule |
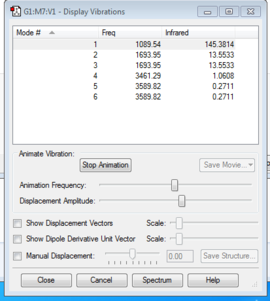
Vibrational Modes in NH3 molecule
From the 3N-6 rule, the molecule is expected to have 6 vibrational modes, as the N in this case is 4. This coincides with the data obtained from computational analysis of the molecule. As can be seen from the table, although there are 6 vibrational modes, the mode 2&3 and 5&6 have the same frequency, therefore they are degenerate. The bending modes are the modes 1,2 and 3. The rest, being 4,5 and 6 are stretching modes. From the animations, it is found that the modes 1 and 4 are highly symmetrical. In addition the vibrational mode 1 is observed to be an "umbrella" mode. The molecule is expected to have 2 bands in the infrared spectrum obtained experimentally, as there are only 3 vibrational modes that has a significant intensities that are observable in the spectrum, and two of the modes are degenerate.
Charge Distribution
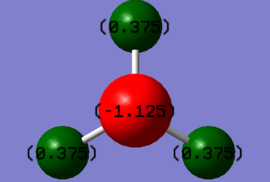
For the molecule NH3, the charge distributed in each species are different. The charge on the H atom is +0.375, and the charge on N is -1.125. The nitrogen atom is expected to be negatively charged as it is more electronegative than the H atom, hence there is a greater electron cloud surrounding the nitrogen nucleus than the hydrogen nucleus, due to a greater attraction of electrons in the valence bond towards the nitrogen's nucleus.
N2 Optimization
General Data
The following method is used to optimize the N2 molecule:
Calculation Method : RB3LYP
Basis Set : 6-31G(d,p)
Type of Calculation : OPTF (optimise and frequency analysis)
The information below are the data obtained from the optimization of the N2 molecule using the method mentioned above:
Final Energy E(RB3LYP) in atomic units (au) : -109.52412868 a.u
RMS Gradient Norm : 0.00000060 a.u
Point Group of NH3 : D∞h
And the following are the bond data obtained:
N-N bong length : 1.10550 Å
H-N-H bond angle : The molecule has no bond angle as it is diatomic molecule
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.401039D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1055 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
The attached data above confirmed that the structure converged.
N2 molecule |
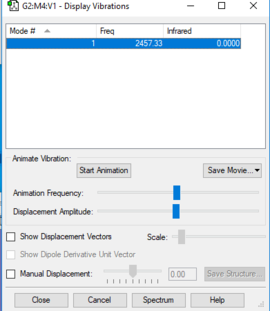
Vibrational Modes in N2
According to the 3N-5 rule, there are suppose to be 1 vibrational mode in the N2 molecule, which turns out to be true when we carry out computational analysis on the molecule. This vibrational mode is simply a symmetrical stretch. As the molecule is symmetrical and diatomic, this vibration would not show in infrared spectroscopy, as the dipole moment of the molecule does not change when the vibration occurs. This is also apparent in the table above, as the intensity found from the vibration is zero.
Charge Distribution in N2
The charge, or in other words electron density in N2 molecules is equally distributed between the two atoms. This is to be expected as both the atoms has the same electronegativity, hence the electron cloud is pulled towards its respective nuclei equally.
H2 Optimization
General Data
The following method is used to optimize the H2 molecule:
Calculation Method : RB3LYP
Basis Set : 6-31G(d,p)
Type of Calculation : OPTF (optimise and frequency analysis)
The information below are the data obtained from the optimization of the H2 molecule using the method mentioned above:
Final Energy E(RB3LYP) in atomic units (au) : -1.17853936 a.u
RMS Gradient Norm : 0.00000017 a.u
Point Group of NH3 : D∞h
And the following are the bond data obtained:
H=H bong length : 0.74279 Å
bond angle : The molecule has no bond angle as it is diatomic molecule
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.164080D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.7428 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
The attached data above confirmed that the structure converged.
H2 molecule |
Vibrational Modes in H2
Using the 3N-5 rule for the linear molecule H2, it is predicted to have 1 vibrational mode, which is found out to be true from computational analysis of the molecule. The molecule is diatomic and the only vibrational mode is a symmetrical stretch. Hence again like the N2 molecule, there won't be any peaks shown in infrared spectrum due to lack of change in the dipole moment of the molecule when vibrations occur. This is also shown in table above, where the intensity of the vibration is zero.
Charge Distribution in H2
The charge is equally distributed throughout the H2 molecule like the N2 molecule. This is again due to the molecule being linear and both atoms having the same electronegativity. Hence the electron cloud is equally distributed throughout the molecule.
Reaction Energies of Molecules
Reaction energy of the Haber Process
The reaction energy of the Haber process can be calculated from the energies found from the computational analysis of N2, H2 and NH3 molecules. The following are the energies found in atomic units :
E(NH3) = -56.55776873 a.u
2*E(NH3) = -113.11553746 a.u
E(N2) = -109.52412868 a.u
E(H2) = -1.17853936 a.u
3*E(H2) = -3.53561808 a.u
ΔE=2*E(NH3)-[E(N2)+3*E(H2)] = -0.0557907 a.u
Converting the energy in atomic units to kJ/mol by multiplying it by 2625.5, the reaction energy is found out to be -146.48 kJ/mol (rounded to 2 d.p). As the energy is a negative value, it shows that the transition from the gaseous reactants to the NH3 molecule actually lowers the overall energy of the system. This means that the energy of the product, being NH3, is more stable than its respective gaseous reactants.
Water Molecule - H2O
In this exercise, I choose the water molecule, H2O due to its importance to life on our planet.
General Data
The following is the method used to analyze the molecule using GaussView and Gaussian software:
Calculation Method : B3LYP
Basis Set :6-31G(d,p)
Type of Calculation : OPTF (optimise and frequency analysis)
The following are the data obtained from the analysis:
Final Energy E(RB3LYP) in atomic units (au) : -76.41973740 a.u.
RMS Gradient Norm : 0.00006276 a.u.
Point Group of NH3 : C2V
And the following are the bond data obtained:
O-H bong length : 0.96522 Å (same length for both O-H bonds)
H-O-H bond angle : 103.745°
Item Value Threshold Converged?
Maximum Force 0.000099 0.000450 YES
RMS Force 0.000081 0.000300 YES
Maximum Displacement 0.000128 0.001800 YES
RMS Displacement 0.000120 0.001200 YES
Predicted change in Energy=-1.939669D-08
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.9652 -DE/DX = 0.0001 !
! R2 R(1,3) 0.9652 -DE/DX = 0.0001 !
! A1 A(2,1,3) 103.7454 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
The above data shows that the structure converged.
H2O molecule |
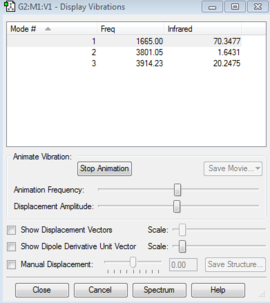
Vibrational Modes
Based on the 3N-6 rule for predicting the number of vibrational modes for non-linear molecule, it is predicted to have 3 modes, which is found out to be true based on its computational analysis. The modes include bending, asymmetrical stretching and symmetrical stretching. From the table, mode number 2 has a very low intensity in the infrared spectrum. This is the symmetrical stretch. The intensity is suggested to be small because the change in the dipole moment resulted from the vibration of the molecule is small, hence absorption of the radiation is small.
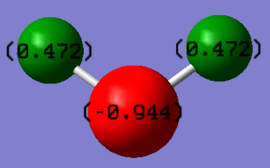
Charge Distribution
As can be seen above, the charge of the oxygen is -0.944 and +0.472 for both the hydrogen. This is to be expected as oxygen is more electronegative than hydrogen, hence there is a greater attraction of the valence electrons to the oxygen nucleus. As a result, there is a greater electron cloud drawn towards oxygen, making it negatively charged. In additional to this, it can be seen that the charge of nitrogen on the NH3 molecule is more negative than the charge of the oxygen in the water molecule. This is due to a greater number of hydrogen atoms in NH3, hence there is a greater electron cloud around the nitrogen atom, making it more negatively charged.
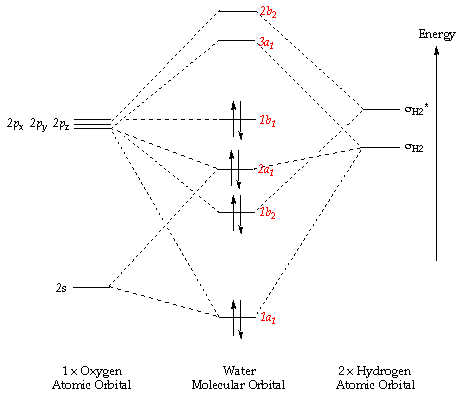
MO diagram of H2O molecule
Reference: Professor Henry S. Rpeza 'Pericyclic Chemistry' on-line lecture course from Imperial College London. The link to the on-line lecture note can be found here: http://www.ch.ic.ac.uk/vchemlib/course/mo_theory/
The above diagram shows the MO diagram of the H2O molecule. The method carried out to derive the MOs is the LCAO method. As the molecule is polyatomic, the Ligand Field Theory (LFT) is used to construct the MO diagram of H2O, taking the oxygen as the central atom and linearly combining the two 1s AO of the hydrogen atoms to form the sigma and sigma star MO. The two MO formed is further combined with the AOs of oxygen to create the MO diagram of the H2O molecule.
Molecular Orbitals of H2O
MO#1 (not shown in MO diagram)
This is the first MO of the H2O molecule. It represents the 1s AO of the oxygen atom as it has not interacted with the other AOs due it its high energy difference between the other orbitals. It is a non-bonding orbital as the orbital has not lowered energy of the overall MO system.
MO#2 (1a1)
This is the first bonding MO of the molecule H2O. As the energy gap of the 2s AO of oxygen is large compared to the other orbitals, it does not combine with the other linearly combined MOs of the two hydrogen atoms. It fact it interacts (mixes) with the bonding MO of the combined orbitals of the oxygen 2p orbital with the other combined MOs of the two hydrogen atoms. This is possible since the pair have the same symmetry. This lowers its energy, making it a bonding MO.
MO#4 (2a1)
This is the fourth MO in the H2O molecule. It is resulted from linearly combining the 2p AO of oxygen with the bonding sigma orbital of the 2H MO. This results in a bonding MO which further mixes with MO#2 mentioned above, raising its energy.
MO#5 (1b1)
This MO is resulted from the 2p orbital alone, representing purely the energy of the 2s. This is due to the AO not having a pair of MO from the combined 1s orbitals of the 2 hydrogen to combine with. It does not mix with the other MO as it has different symmetry compared to the other MOs. This MO is important as it is the valence MO, in other words it is the highest occupied molecular orbital (HOMO) of the molecule. This MO determines the chemical reactions that the molecule further undergo.
MO#6 (3a1)
This MO is the lowest unoccupied molecular orbital (LUMO) of the molecule. Again, it is important in the further reactions that H2O undergoes. It is an anti-bonding MO and does not undergo mixing due to the lack of MO with the same symmetry. This MO is resulted from the anti-phase linear combination of the oxygen 2p AO and the bonding MO of the two combined 1s AO of the other two hydrogens.