Rep:Mod:PKOorganic1
ə==Introduction==
Hydrogenation of cyclopentadiene dimer
Dimerization
The dimerisation of cyclopentadiene occurs spontaneously at room temperature. The reaction is a Diels-Alder [4+2] cycloaddition, and as the pericyclic system contains 6 π-electrons, a Hückel transition state is favoured. The reaction is stereospecific, with either endo- or exo- forms of the dimer being possible products; the stereochemistry is defined by the position from which the dienophile attacks. The two mechanisms of cycloaddition and the corresponding products are shown in figure 1.
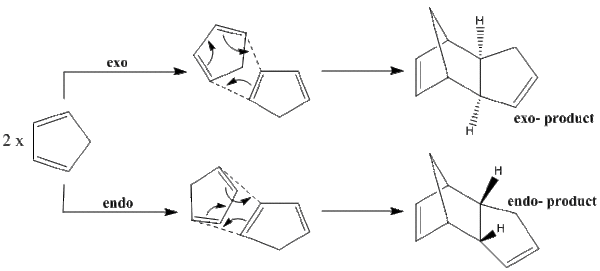
The MM2 force field calculation in ChemBio3D has been performed on both isomers in order to minimize the energy, and the results of the calculations are shown in table 1. Figure 2 displays the optimized geometry of each isomer.
| Energy type | Energy of exo product / kcal/mol | Energy of endo product / kcal/mol |
|---|---|---|
| Stretch | 1.2845 | 1.2505 |
| Bend | 20.5799 | 20.8470 |
| Stretch-bend | -0.8381 | -0.8353 |
| Torsion | 7.6562 | 9.5113 |
| Non-1,4 VDW | -1.4186 | -1.5450 |
| 1,4 VDW | 4.2350 | 4.3213 |
| Dipole/Dipole | 0.3775 | 0.4477 |
| Total | 31.8765 | 33.9975 |
From these results we can see that the exo product has the lower total energy, with a difference of 2.121kcal/mol between the two isomers. This would suggest that the exo product is the more stable isomer and therefore the thermodynamic product. However, the literature commonly accepts that the major product is the endo product; this suggests that the reaction proceeds under kinetic control. The stereochemistry of pericyclic reactions is often determined by the relative stability of the transition states, and the endo rule states that for a Diels-Alder reaction, the endo transition state will have the lowest energy, and the reaction will proceed via this transition state. This explains why the reaction occurs under kinetic control, and thus why the higher energy isomer is in fact the major product.
Hydrogenation
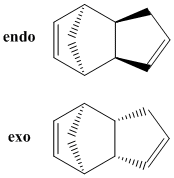
Molecules 3 and 4 are the possible products of dihydrogenation of one of the double bonds of the dimer. Their energies were calculated with MM2 and found to be 35.2446 for molecule 3 and 31.0136 for molecule 4. THis shows that molecule 4 is 4.231kcal/mol lower in energy than molecule 3 and is therefore more stable. This is most likely explained by the fact that the bond angle in 4 is nearer to the ideal bond angle for double bond of 120o than it is in 3, where is it part of a norborene and experiences more strain. This theory is supported by the fact that the bond energy showed the largest differensce between the energies of the two molecules.
Intermediate stereochemistry and reactivity in taxol synthesis
The synthesis of Taxol proposed by Paquette provides an example of atropisomerism; one of the key intermediates can exist as atropisomers, a unique form of stereoisomers which arise due to high steric demand preventing rotation around a normally free single bond. The two atropisomers are shown below.

Both isomers were drawn in ChemBio3D and their energies minimised with the MM2 calculations. These energies were further minimised by changing the geometry shown, for example to make the 6-membered ring adopt a chair conformation. The calculated energies are shown in the table below.
| Energy type | Energy of 9 / kcal/mol | Energy of 10 / kcal/mol |
|---|---|---|
| Stretch | 2.8707 | 2.6390 |
| Bend | 15.8814 | 12.5514 |
| Stretch-bend | 0.3566 | 0.4248 |
| Torsion | 18.4362 | 19.1240 |
| Non-1,4 VDW | -0.4954 | -1.6077 |
| 1,4 VDW | 13.2436 | 12.8587 |
| Dipole/Dipole | -1.7717 | -1.7013 |
| Total | 48.5213 | 44.2888 |
These show 10, which has the carbonyl group pointing down, to be the more stable isomer. This can be explained due to the steric repulsion experienced by the carbonyl in 9; both the hydrogen atoms and the methyl group in the bridgehead can interact with the carbonyl in the up position and raise the energy of the isomer. In 10, the carbonyl group points down and therefore avoids this negative interaction, making it the lower energy of the pair.
The calculations were repeated using the MMFF94 force field. This gave energies of 68.4627 kcal/mol for isomer 9, and 62.2627 kcal/mol for 10, showing that 10 is still the more stable isomer. The energy difference for the two isomers is 5.20 for the MMFF94, and 4.23 for the MM2 calculation.
Whilst the strain caused by the presence of the bridgehead would suggest that the alkene would be fairly unstable and therefore react quite readily, studies have shown the alkene to be extremely unreactive. In order to further investigate the reasoning behind it, MM2 calculations were also carried out on the corresponding alkane, created by hydrogenating the alkene to convert the double bond to a single bond. This also found the isomer with the carbonyl pointing down to be the more stable, however the energies for the hydrogenated versions of 9 and 10 were 70.2 kcal/mol and 65.6 kcal/mol respectively. The unexpected stability of the alkenes compared to the equivalent alkane can be attributed to the fact that the intermediate is a hyperstable alkene. This is an alkene that has less strain that its parent saturated hydrocarbon; whilst normally olefins at bridgehead positions would be expected to have a high strain, in a large cyclic system the increased interactions with hydrogen atoms stabilise the molecule.
Modelling using semi-empirical MO theory
The calculations used so far have been based on a molecular mechanics model. This, however, is unable to account for electronic interactions of a molecule. In this section, the various electronic interactions and their effects on the reactivity of a molecule will be taken into account.
Regioselective addition of Dichlorocarbene
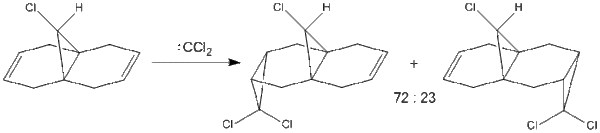
The addition of 9-chloromethanonaphthalene to dichlorocarbene, shown below, has been shown by Halton et al. to proceed with the formation of 72% of the syn-trichloride, thus showing high regioselectivity. The reaction and possible products are shown here:
MOPAC/PM6 calculations were used in order to obtain an approximate representation of the valence-electron molecular orbitals. As the HOMO has the greatest effect on the reactivity of the molecule, particular attention will be paid to this. Diagrams of the HOMO, LUMO, HOMO-1, LUMO+1 and LUMO+2 are shown below:
 |
 |
 |
 |
 |
The reaction shown above is an electrophilic addition reaction, and will therefore take place with attack at the most nucleophilic alkene. By examining the picture of the HOMO, we can see that the electron density is concentrated around the alkene syn to the chlorine atom, and is particularly low around the double bond in the anti position. The regioselectivity of the reaction can be determined by the relative energies of the two alkene orbitals, and the higher energy orbital is the one attacked by the electrophile. The driving force for this was found by Halton et al [1] to be due to the stabilising interactions between the C-Cl σ* orbital and the occupied π-orbital of the anti alkene, which render the syn alkene more nucleophilic and therefore more likely to be the site of attack.
Vibrational frequencies
In order to calculate the effect of the C-Cl bond on the vibrational frequencies of the molecule, the stretching frequencies have been calculated for molecule 12, and compared to those for molecule 12A, where the anti double bond has been hydrogenated. An MM2 calculation was used initially, and then B3LYP/6-31G(d,p) Gaussian geometry optimization and frequency calculations were performed.
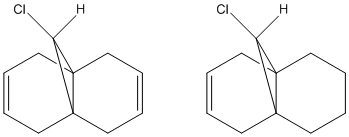
The stretching frequencies obtained for molecules 12 and 12A are shown in the following table:
| Molecule | Syn C=C stretch / cm-1 | Anti C=C stretch / cm-1 | C-Cl stretch / cm-1 |
|---|---|---|---|
| 12 | 1757.60 | 1737.30 | 770.90 |
| 12A | 1758.10 | - | 774.90 |
From this we can see that the syn double bond has a higher frequency than the anti double bond, meaning it has a higher bond order and is stronger. Also, the C-Cl bond has a higher frequency when the anti double bond is not present. These observations can both be explained by the stabilising interaction described previously, between the C-Cl σ* orbital and the occupied π-orbital of the anti double bond; as electron density moves from the double bond π-orbital the bond order is decreased and the bond weakened, and likewise as the electron density increases in the σ* orbital of the C-Cl bond, the σ bond will be weakened.
The fact that the syn C=C bond stretches in 12 and 12A only differ by a small amount suggests that the presence of a second double bond has little effect on the strength of the syn alkene.
Monosaccharide chemistry: glycosidation
During glycosidation, atom X is replaced by a nucleophile, which can add in either the α or β anomer being formed. The presence of an acetyl group on the neighbouring carbon atom can force the reaction to occur stereospecifically. The mechanism and possible products are shown below:
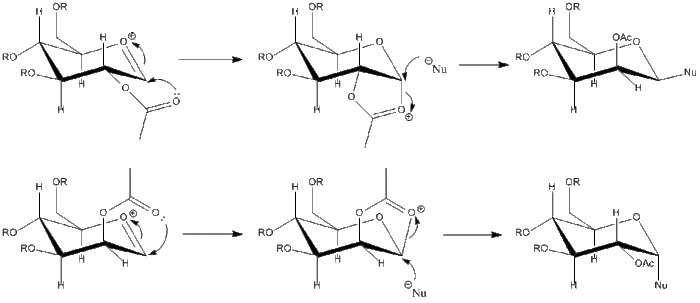
Analysis of the two conformers of the oxonium cation will be used here to find out which is the more stable conformer. A methyl group will be used as the R group, since it is desirable to keep the size of the molecule as small as possible in order keep the calculation as simple and fast as possible. The MOPAC/PM6 calculation will give the best approximation of the energy of the molecules, since the differences are caused by orbital interactions, which the MM2 calculation does not take into account. In the following table, energies calculated by both MM2 and MOPAC/PM6 have been calculated for A and B (where the acyl group points below the plane of the oxonium ion), and also for A* and B*, where the acyl group points above the plane of the oxonium ion. This was also carried out on intermediates C and D, and C* and D*. All the energies are shown in the following table:
| Molecule | MM2 energy / kcalmol-1 | MOPAC/PM6 energy / kcalmol-1 |
|---|---|---|
| A | 24.4762 | -68.8453 |
| A* | 35.8104 | -75.6335 |
| B | 21.0592 | -73.2745 |
| B* | 30.6743 | -75.8231 |
| C | 29.2849 | -91.0353 |
| C* | 44.0232 | -91.0576 |
| D | 34.3059 | -75.9354 |
| D* | 42.0563 | -88.6349 |
As we can see, A, B, C, and D are all lower in energy than their counterparts with the acyl group pointing above the plane of the oxonium ion. This can be explained by the fact that when the carbonyl is out of the plane, it is unable to stabilise the ion and therefore these structures have a higher eneryg. A and B can also be seen to be lower in energy than their relative intermediates C and D.
Structure-based mini project
Here, molecular orbital methods will be used to investigate the regioselectivity of a reaction where two isomers can be formed. The reaction being investigated involves click chemistry, which was introduced by Barry Sharpless in 2001 and uses small molecules or units being "clicked" together in order to create larger molecules quickly and in high yield. The relative energies, as well as the spectroscopic data, can be modelled and compared to the literature.
Assigning regiomers in "click chemistry"
The reaction to be studied here, shown below, is a 1,3-dipolar cycloaddition between an azide and an alkyne to give a 1,2,3-triazole, and was found in 2002 to be sped up by the use of a Cu(I) catalyst.

The use of a copper catalyst was found to cause the formation of isomer A as the major product. However, it has also been reported by Zhang et al. that the use of a Ruthenium catalyst causes isomer B to predominate.
NMR analysis
In order to obtain a representation of the 13 C spectrum of a compound, the GIAO approach is used, which uses quantum mechanical density functional theory. Each isomer was drawn in ChemBio3D and an initial MM2 geometry optimization performed. A Gaussian input file is then created to run the DFT=mpw1pw91 method. After initially calculating a minimised energy, the input file was changed to account for the NMR solvent used and the job submitted to the SCAN server. The resulting output file allows us to see an NMR spectrum based on the predicted chemical shifts. The spectra predicted for each isomer are shown below:
The literature results for the chemical shifts can be compared with the predicted values in the following tables:
| Computed δ / ppm | Literature δ / ppm |
|---|---|
| 52.0 | 54.0 |
| 115.1 | 120.0 |
| 118.6 | 126.0 |
| 119.9 | 128.0 |
| 121.7 | 128.5 |
| 122.2 | 129.0 |
| 122.6 | 129.0 |
| 123.0 | 129.5 |
| 125.1 | 131.0 |
| 130.5 | 135.0 |
| 142.2 | 148.5 |
| Computed δ / ppm | Literature δ / ppm | |
|---|---|---|
| 49.7 | 51.85 | |
| 122.2 | 126.93 | |
| 122.3 | 127.22 | |
| 122.5 | 128.22 | |
| 122.9 | 128.92 | |
| 123.0 | 129.08 | |
| 123.2 | 129.64 | |
| 123.6 | 133.26 | |
| 126.0 | 133.34 | |
| 131.8 | 135.66 | |
| 134.0 | 138.26 |
IR analysis
IR analysis can also be performed and compared to the literature spectra. Due to time constraints, this calculation has not been carried out, but further work could involve comparing the IR spectra for the two isomers and analysing the effect of the position of the R group on the stretching frequencies of the molecules.
Conclusion
The work undertaken in this module has proven that computational techniques can be successfully used to investigate the differences between isomers of reaction products and data such as energies and bond stretching frequencies can be used to rationalise selectivity in the reactions mentioned here. The mini-project has shown that 13C NMR calculations are in good accordance with the literature.
- ↑ B. Halton, R. Boese, H.S. Rzepa., J. Chem. Soc., Perkin Trans 2, 1992, 447. DOI:10.1039/P29920000447
