Rep:Mod:PHYYLC1016

The Cope Rearragnement

Figure 1: Cope rearrangement of 1,5 hexadiene

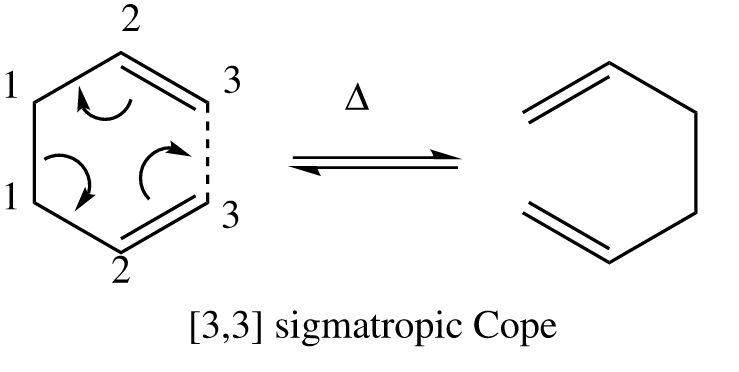
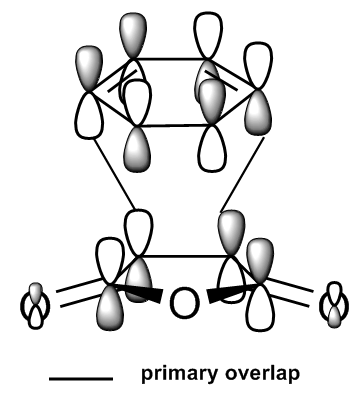
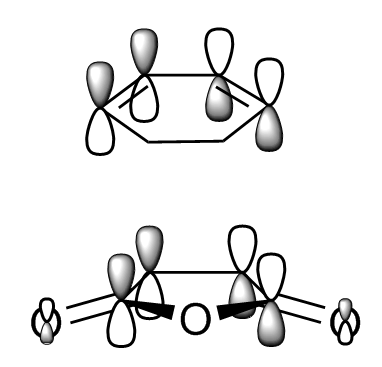
The cope rearrangement of 1,5 hexadiene is known to be an [3,3] sigmatropic shift with mechanism shown in Figure 1. The reaction generally occurs through a chair or boat transition state (TS) in a concerted manner. For the investigation of which transition state is more favourable, their structures were first optimised, followed by vibrational analysis. Based on the computed activation energies of the transition states, it found out that the chair TS has lower energy. This is matched with what we expected as chair conformation tends to have lower energy compared to the boat conformation.

Optimising the reactants and products

Introduction

The structure of 1,5 hexadiene, which is both reactant and product, was first optimised at the HF/3-21G level , followed by B3LYP/6-31G* level for locating the lowest energy conformation. A series of low energy conformers (see Table 1) were obtained from the optimisation and their identities were verified from the Appendix 1 . In order to compare the computed energy with the experimental value, frequency analysis was also carried out for each conformer.

Result and Discussion

Table 1:Energies and Structures of different conformers of 1,5 hexadiene

Conformers	Anti 1	Anti 2	Gauche 3	Gauche 4
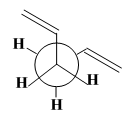
Newman projection of the conformers
Structure ( HF/3-21G )	Vibration	Vibration	Vibration	Vibration
Total energy ( Hartrees )	-231.69260236	-231.69253528	-231.69266120	-234.69153032
Relative energy to Gauche 3 (kcal/mol)	0.04	0.08	0.00	0.71
Log File	File:REACT ANTI LINKAGE ANTI 1.LOG	File:REACT ANTI LINKAGE ANTI 2.LOG	File:REACT GAUCHE 3 LINKAGE.LOG	File:REACT GAUCHE 4 LINKAGE.LOG
Structure ( B3LYP/6-31G* )	Vibration	Vibration	Vibration	Vibration
Total energy ( Hartrees )	-234.61179055	-234.61170280	-234.61132934	-234.61048196
Relative energy to Gauche 3 (kcal/mol)	-0.29	-0.23	0.00	0.53
The sum of electronic and zero-point energies at 0 K (Hartrees)	-234.469298	-234.469212	-234.468693	-234.467784
The sum of electronic and thermal energies at 298.15 K (Hartrees)	-234.461966	-234.461856	-234.461464	-234.460521
Point Group	C2	Ci	C1	C2
IR spectrum
Log File	File:DFT ANTI 1 LINKAGE.LOG File:FREQ ANTI 1 LINKAGE.LOG	File:DFT ANTI 2 LINKAGE.LOGFile:FREQ ANTI 2 LINKAGE.LOG	File:DFT GAUCHE 3 LINKAGE.LOGFile:FREQ GAUCHE 3 LINKAGE.LOG	File:DFT GAUCHE 4 LINKAGE.LOGFile:FREQ GAUCHE 4 LINKAGE.LOG

For the judgement on whether low energy conformer was obtained from the optimisation, it can be done through two ways. Firstly, checking all forces and displacement are converged from log file of the optimisation process. Secondly, comparing electronic energies of the conformers to data shown in the Appendix 1 and see good matches obtained or not. The lower energy conformer was further confirmed by the frequency analysis; its vibrational frequencies are all real and positive, i.e. without any imaginary frequencies.

By looking down the central C-C bond, the conformers can be split into two main groups, Anti and Gauche forms. The geometries of the optimised structure were very similar for both basis sets and the central C-C bond in computed structure were approximately identical (0.155 nm) in 2 decimal places. This indicated that the central C-C bond length is insensitive to both basis set and the orientation of the terminal C=C bond (regardless it is anti or gauche). However, the electronic energies of the optimised conformers were sensitive to basis set. Optimised structure tend to have higher total energy at B3LYP/6-31G* theory (about 0.008 Hartrees higher, see Table 1). The difference in total energies also resulted the lowest energy conformer being either Gauche 3 ( for HF/3-21G basis set) or Anti 1 (for B3LYP/6-31G* basis set) . Despite this, electronic correlation was accounted at B3LYP/6-31G* basis set, so it is a higher level theory compared to HF/3-21G ,hence suggesting Anti 1 is the lowest energy conformation of 1,5 hexadiene instead of Gauche 3. This was matched to what we expected from the Newman projection; Anti conformation generally has lower energy due to the presence of stabilising δ _C-C orbital to π * orbital interactions and the least steric hindrance in space between the two terminal C=C bond. As the stabilisation effect from interaction between δ _C-C orbital and π * orbital were overlooked in the HF/3-21G optimisation , the Gauche 3 conformation was favoured initially. After reoptimisation at B3LYP/6-31G* level and accounted for electronic correlation, Anti 1 became the most favourable. From the relative energies of the anti conformer at B3LYP/6-31G* level, Anti 1 is more stable than Anti 2 conformer. This can be explained by the orientation of the terminal C=C bond. The two terminal C=C bond are in the same orientation in Anti 1 (shown in Newman projection, Table 1) and this enables the π to π * interaction to happen. This interaction is less pronounced for anti 2 conformer, hence it is less stable.

Optimising the Chair and Boat Transition structures

Introduction

Figure 2: Chair and Boat Transition state for cope rearrangement of 1,5 hexadiene

For both chair and boat TS, there have two C₃H₅ allyl fragments positioned in around 2.2 Å from each others. Based on the structure of C₃H₅ allyl fragment, TS was optimised through two different methods, normal optimisation and frozen coordinated method. While boat TS was optimised by QST2 method from the structure of anti 2 conformer of 1,5 hexadiene. Same as before, the optimisation was carried out at HF/3-21G basis set initially and followed by B3LYP/6-31G* . Basis set B3LYP/6-31G* was specially used here due to it has been shown to give energies terms in a good agreement with the experimental values

Results and Discussions

Table 2:Optimisation and Frequency analysis of Chair transition state

Method	Normal Optimisation		Frozen Coordinated
Basis Set	HF/3-21G	B3LYP/6-31G*	HF/3-21G	B3LYP/6-31G*
Structure
Length between terminal ends (Å)	2.02	1.97	2.02	1.97
C-C bond length in the fragment (Å)	1.39	1.41	1.39	1.41
Point Group	C2h	C2h	C2h	C2h
The sum of electronic and zero-point energies at 0 K (Hartress)	-231.466699	-234.414929	-231.466701	-234.414929
The sum of electronic and thermal energies at 298.15 K (Hartress)	-231.461340	-234.409009	-231.461342	-234.409009
Imaginary Frequency(cm-1)	-818.0367	-565.5418	-818.0325	-565.5416
Log File	File:CHAIR TS GUESS OPTIMISED YLC.LOG	File:CHAIR TS GUESS OPTIMISED YLC - B3L.LOG	File:CHAIR TS GUESS FROZEN MIN YLC - 2.LOG	File:CHAIR TS GUESS FROZEN MIN YLC - 2 - B3L.LOG

Table 3:Optimisation and Frequency analysis of Chair transition state

Method	QST2
Basis Set	HF/3-21G	B3LYP/6-31G*
Structure
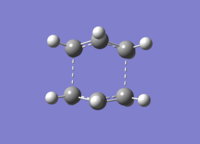Length between terminal ends (Å)	2.14	2.21
C-C bond length in the fragment (Å)	1.38	1.39
Point Group	C2v	C2v
The sum of electronic and zero-point energies at 0 K (Hartress)	-231.450928	-234.402342
The sum of electronic and thermal energies at 298.15 K (Hartress)	-231.445299	-234.396007
Imaginary Frequency(cm-1)	-839.9356	-530.2989
Log File	File:BOAT TS QST2 2 YLC.LOG	File:BOAT TS QST2 2 YLC - B3L.LOG

Frequency analyses were carried out for each optimised TS structure and all of them consist of imaginary frequencies in their vibrational mode, this indicated that transition state was achieved for each case. From Table 2 and 3, it can be seem that chair TS had a more negative electronic energy than boat TS, so it is more stable. This is because the two allyl fragments are staggered in chair TS and they experiences less steric strain compare to eclipsed relationship in boat conformation. Moreover, the larger steric strain within the boat TS results a longer distance between the terminal ends of the ally fragments ( 0.12 Å longer than chair TS). The distance also is subjected to the type of basis set used for the optimisation, i.e. longer distance was observed at HF/3-21G theory. However, all the distance is shorter than sum of van der waals radii of two sp2 hybridised C atoms(3.40 Å) and longer than sum of covalent radii (1.46 Å) . This reflected that a bond is being formed or broken between C atom in terminal ends. Furthermore, the C-C bond length within the allyl fragment lie between standard C-C (1.54 Å) and C=C (1.30 Å) , this implied that the fragment has a partial double bond character, hence delocalisation of π electron.

Two methods (normal optimisation and frozen coordinated method) were employed in the optimsation of chair TS, both gave exactly the same optimised structure with same electronic energies and bond length. This could suggest that they both are good ways in determination of the chair TS structure.

After frequency analysis of the optimised TS structures, the vibrational mode of each TS can be visualised (see Figures 3, 4 and 5 below). This allowed formation and breakage of bonds in the cope rearrangement to be observed. To be notice that the vibrational modes are very similar for both chair and boat TS, carbon atoms in the one side of the terminal ends move toward each other in a concerted manner to form a bond. In the same time, the other side of the terminal ends was forced to move apart to break a bond.

Figure 3: Vibration mode of Chair Transition state (Normal optimisation)

Figure 4: Vibration mode of Chair Transition state (Frozen coordinate)

Figure 5: Vibration mode of Boat Transition state

Finding the Conformer form of the Chair Transition State

Introduction

Based on the transition states obtained above, it is hard to predict which conformer of 1,5-hexadiene will be lead to in following the reaction path. Despite this, Intrinsic Reaction Coordinate (IRC) method enables the minimum energy path from a transition state to its local minimum to be followed on a potential energy surface. This is done by creating a series of small geometry steps in the direction where the energy surface with the steepest slope. Optimised chair transition state form normal optimization at HF/3-21G theory was selected to undergoes IRC in a forward direction (50 steps) only due to symmetrical reaction coordinates.

Results and Discussion

Table 4:Results of Intrinsic Reaction Coordinate (IRC) Analysis

	IRC	Normal minimisation of last point of IRC
Structure	Vibration	Vibration
Point group	C2h	C2
Dihedral angle (degree)	67.2	64.2
Electronic energy (a.u.)	-231.61932229	-231.69166702
IRC Path		N/A
Log File	File:CHAIR TS GUESS OPTIMISED YLC - ISC.LOG	File:CHAIR TS GUESS OPTIMISED YLC - ISC - opt.LOG

The results were summarised in the Table 4 above. After the ISC calculation, a conformer of 1,5-hexadiene with a close structure to Gauche 2 was obtained. However, it had a slightly higher energy compared to the one of Gauche 2 listed in Appendix 1 . This implied that it has not reached minimum geometry yet. In order to reach the minimum geometry, last point of the IRC calculation was taken to run a normal optimisation process at HF/3-21G basis set. A structure with a lower energy than the last point of the IRC was given, it also had exactly same energy and symmetry as Gauche 2 (see Appendix 1 ). This confirmed that the last point of the initial IRC calculation was not a local minimum and further optimisation does help in achieving the minimum geometry, which is Gauche 2 in this case. The dihedral angle of the conformer was slightly reduced upon optimisation as well and this might the origin in minimising the energy. Thereby, Gauche 2 is the conformer that chair Transition state lead to in this cope rearrangement reaction.

Activation Energies for each transition state

Introduction

The activation energies for the cope rearrangement reaction via chair and boat transition state were obtained from the result of the frequency analysis of the optimised TS at HF/3-21G and B3LYP/6-31G*level of theory. The calculated results and experimental comparison were summarised in below.

Results and Discussion

Table 5:Comparison of the computed activation energies to experimental values

	Chair TS							Boat TS
	at 0 K		at 298.15 K		at 313.15 K			at 0 K		at 298.15 K		at 313.15 K
Basis Set	HF/3-21G	B3LYP/6-31G*	HF/3-21G	B3LYP/6-31G*	HF/3-21G	B3LYP/6-31G*		HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	HF/3-21G	B3LYP/6-31G*	HF/3-21G
Computed Ea	45.71	34.06	44.69	33.16	44.65	33.12		55.60	41.96	54.80	41.32	54.73	41.31
Experimental Ea	33.5±0.5		N/A		N/A			44.7±2.0		N/A		N/A
Percentage difference to Experimental value	36.4	1.68	N/A	N/A	N/A	N/A		24.4	-6.13	N/A	N/A	N/A	N/A

The activation energies at three different temperature were calculated based on the energy of Anti 2 conformer (listed in Table 1) as Anti 2 conformer was used specially in the locating the boat TS. Energy terms at 0 K and 298.15 K were obtained from the frequency analysis of the optimised structure whereas energy terms at 313.15 K was computed using ‘’’ Freqcheck’’’ function in Gaussian09. The computed activation enegies of chair TS are smaller than the boat TS one regardless the basis set used and the temperature it under. This implied that the cope rearrangement of 1,5 hexadiene happen via chair TS preferially. The activation energies at 0 K computed using B3LYP/6-31G* had much smaller percentage difference to the experimental(<± 7%). This confirmed that B3LYP/6-31G* is a better theory in calculating electronic and thermal energies than HF/3-21G and it is a good theory for this reaction. However, optimising the structure first at HF/3-21G theory, then reoptimising at B3LYP/6-31G* is a more computational efficient way to do so. From the Table 5, the computed activation energies increased with temperature was observed.

The Diels Alder Cycoaddition

The Diels Alder Cycloaddition is an example of pericyclic reaction, with [4+2] mechanism. The reaction generally happens between a diene and dieneophile and σ bond will be formed between their π-orbitals. From the molecular orbital point of view, HOMO/LUMO of one of the reactant (i.e. diene or dieneophile) interacts with LUMO/HOMO of another reactant in forming a new set of bonding and antibonding MO. If the reaction proceeds thermally, Huckel topology will be applied to the stereochemistry, i.e. with suprafacial components only. This explained why the Diels Alder Cycloaddition occurs in a concerted stereospecific fashion. Whether the reaction is allowed or forbidden is depended on two factors. Firstly, the number of π electron involve in the reaction can be important. The number of π electron need to be fitted in 4n+2 rule (where n=1 in this case) under thermal condition or fitted in 4n rule under photochemical condition. Secondly, the HOMO and LUMO pair needs to have same symmetry for significant overlap between them, hence the reaction can be proceeded. Moreover, it is common that the dieneophile are disubstituted. It is possible for π orbitals on the substituents to interact with the new formed double bond in the product. This π - interaction stabilises the TS of one of the possible regioisomer (Exo or Endo) and lead to its formation preferentially at the end. This is known as the effect of second orbital overlaps.

Cycloaddition between Ethene and Cis-Butadiene

Figure 6: Mechanism of Cycloaddition between Ethene and Cis-Butadiene

Cyclohexene was formed in the cycloaddition of cis-butadiene and ethane. As both substituents on the dieneophile (ethane) are simply H atoms, no second orbital overlap effect is expected to be observed. Therefore, there has no issue of regioselectivity in the product. It was known that the HOMO of ethane and the LUMO of cis-butadiene are both symmetric with respected to the reflection plane whereas the LUMO of ethane and HOMO of cis-butadiene are both antisymmmtric.

Optimisation of Cis-Butadiene

Cis-butadiene was optimised at Semi-empirical/AM1 Semi-empirical molecular method, followed by the B3LYP/6-31G* basis set. The structure and symmetry of the HOMO and LUMO of Cis-butadiene were shown in the Table 6 below.

Table 6:Optimisation of Cis-Butadiene

Basis Set	Semi-empirical/AM1	B3LYP/6-31G*
Optimised Structure	Vibration	Vibration
Electronic Energy (a.u.)	0.04878534	-155.98648970
Point Group	C2	C2
Log File	File:CIS BUTADIENE OPTIMISED AM1 YLC.LOG File:CIS BUTADIENE FREQ AM1 YLC.LOG	File:CIS BUTADIENE OPTIMISED DFT YLC.LOG File:CIS BUTADIENE FREQ DFT YLC.LOG
Structure of HOMO
Symmetry of HOMO	Antisymmetric	Antisymmetric
Structure of LUMO
Symmetry of LUMO	Symmetric	Symmetric

The optimised structure obtained from both methods has the same point group but the dihedral angle along central C-C bond was two times larger for the structure obtained from the B3LYP/6-31G* theory. The structure from B3LYP/6-31G* basis set has much lower energy, so it might suggest this is the minimum geometry of cis-butadiene. The symmetries of plotted HOMO and LUMO are antisymmetric and symmetric respectively, this is exactly the same mentions previously. As the optimised structure from B3LYP/6-31G* theory is more bent in structure, so the obtained MOs is less symmetrical than the one from Semi-empirical/AM1 method.

Optimisation of transition state and examination of the nature of the reaction path

Transition state optimisation was set up by computing the force constants at the beginning of the calculation. Several transition state structures were guessed and modified before achieving successful calculation. It found out that a good guess structure of the transition state can be obtained by modifying the expected product geometry in to the two corresponding reactants structure. Moreover, linear combination of atomic orbitals (LCAO) method was used in given a better illustration on how the frontier orbitals overlap in the TS and results the corresponding HOMO and LUMO structures. The results were summarised in below.

Table 7:Optimisation of Transition state

Basis Set	Semi-empirical/AM1	B3LYP/6-31G*
Optimised Structure
Electronic Energy (a.u.)	0.11165477	-234.54389654
Point Group	Cs	Cs
Distance between terminal ends (Å)(bond length of partially formed σ C-C bond)	2.12	2.27
Imaginary Frequency (cm-1)	-956.26	-525.07
Log File	File:CYCLO 1 TS OPTIMISED AM1 GUESS YLC.LOG	File:CYCLO 1 TS OPTIMISED DFT GUESS YLC.LOG

Table 8:MO of Transition state

Basis Set	Semi-empirical/AM1
MO	HOMO
Structure
Symmetry	Antisymmetric	Antisymmetric
MO	LUMO
Structure
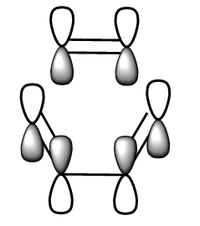
Symmetry	Symmetric	Symmetric

The distance between terminal ends was set to be 2.0 Å in the guess structure and turned out that it is (2.12 Å / 2.27 Å). From Table 7, the distance between terminal ends of the reactants is shorter than sum of van der waals radii of two sp2 hybridised C atoms(3.40 Å) and longer than sum of covalent radii (1.46 Å) . This indicated a C-C sigma bond was partially formed. The bond lengths of C=C bonds within the reactants lies between typical sp3 C-C (1.54 Å ) and sp2 C-C bond (1.30 Å ). This indicated that these bonds are being broken in the transition state. From both theories, optimised geometries were associated with imaginary frequencies, this proved that the structure of transition state was achieved. In addition, the HOMO of TS is constructed from the antisymmetric HOMO of cis-butadiene and anti symmetric π * orbital of ethane, so it is antisymmetric overall. Same for symmetric LUMO, in which is constructed from symmetric LUMO of cis-butadiene and π orbital of ethane. It also can be seem that the electron density was concentrated in the region where new σ C-C bond formed, suggesting there has a good overlap between frontier orbitals, hence this cycloaddition is allowed and via [4s+2s] mechanisms.

The vibrational mode of the TS at Semi-empirical/AM1 were shown below, this enabled the new σ bond formations to be investigated.

Figure 7: IR spectrum of Transition state (AM1)

Figure 8: Vibrational mode of Transition state (AM1)

Figure 9: Lowest real vibrational mode of Transition state (AM1)

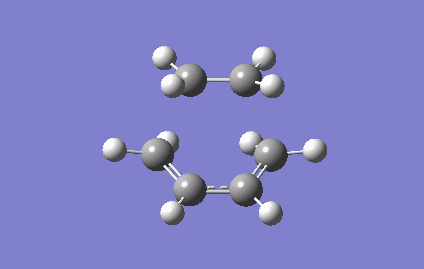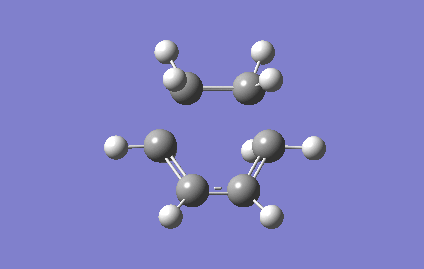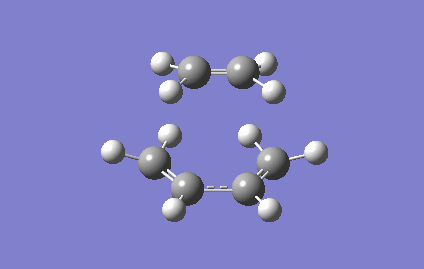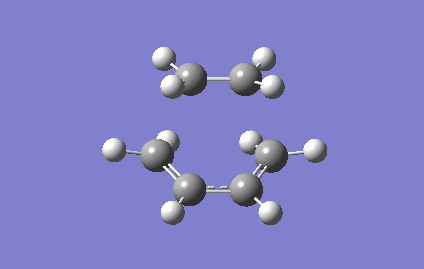
For Semi-empirical/AM1 , the vibrational mode corresponds to the reaction path at the transition state was shown in the Figure 8. The terminal ends of ethene and cis-butadiene were approached to each other in a concerted manner during the vibration, this implied that the two new sigma C-C bonds was formed synchronously. Unlike the stretching modes in the TS vibrational frequency, both molecules were undergoes bending motions at the lowest real vibrational frequency ( 147.09 cm^-1, Figure 9). More structural changes involve in the vibration of the TS, so a higher energy will be needed in causing vibration, hence a larger in magnitude of vibrational frequency was observed for TS.

Cycloaddition between Maleic Anhydride and Cyclohexadiene

Figure 9: Mechanism of Cycloaddition between Maleic Anhydride and Cyclohexadiene

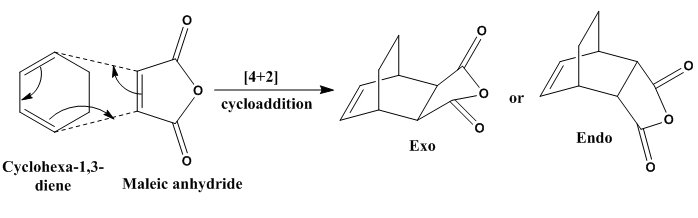
For this cycloaddition, the dieneophile (maleic anhydride) is an electron-withdrawing species, i.e. it is electron deficient, this in turn forcing the regular Diels–Alder cycloaddition. It is di-substituted in nature, so the π orbitsls on the C=O bonds are possible involving in the second orbital overlap effect. Which regioisomer (Exo or Endo) will be preferred in this reaction is dependent on the balance between steric and electronic effects and they were studied below.

Optimistaion of the transition state and study of regioselectivity

The transition state structure for both Exo and Endo were optimised using same methods as for TS in previous cycloaddition reaction. The distance between the C atoms, where the new σ C-C bonds will be formed, were guessed to be 2.2 Å prior the optimisation. The computed results were listed below.

Table 9:Optimisation of Endo and Exo transition state

	ENDO
Basis Set	Semi-empirical/AM1	B3LYP/6-31G*
Structure	Atom C-C bond length/Å C3-C15 1.393 C15-C17 1.397 C17-C2 1.393 C3-C11 2.162 C15-C20 2.892 C17-C19 2.892 C2-C9 2.162 C9-C11 1.409	Atom C-C bond length/Å C3-C15 1.391 C15-C17 1.403 C17-C2 1.391 C3-C11 2.269 C15-C20 2.990 C17-C19 2.990 C2-C9 2.269 C9-C11 1.394
Point Group	Cs	Cs
Electronic energy (a.u.)	-0.05150480	-612.68339679
Imaginary Frequency(cm-1)	-806.4446	-446.8043
Log File	File:CYCLO2 TS OPTIMSED ENDO BEFORE ylc.LOG	File:CYCLO2 TS OPTIMSED ENDO DFT.LOG
	EXO
Basis Set	Semi-empirical/AM1	B3LYP/6-31G*
Structure	Atom C-C bond length/Å C3-C4 1.394 C4-C1 1.397 C1-C2 1.394 C3-C9 2.170 C13-C18 2.945 C15-C17 2.945 C2-C7 2.170 C7-C9 1.410	Atom C-C bond length/Å C3-C4 1.391 C4-C1 1.403 C1-C2 1.391 C3-C9 2.291 C13-C18 3.028 C15-C17 3.028 C2-C7 2.291 C7-C9 1.398
Point Group	Cs	Cs
Electronic energy (a.u.)	-0.05041984	-612.67931096
Relative Electronic energy to ENDO (a.u.)	0.00108496 higher	0.0040858 higher
Imaginary Frequency(cm-1)	-812.0740	-448.4461
Log File	File:CYCLO2 TS OPTIMSED EXO AM1 YLC.LOG	File:CYCLO2 TS OPTIMSED EXO DFT YLC.LOG

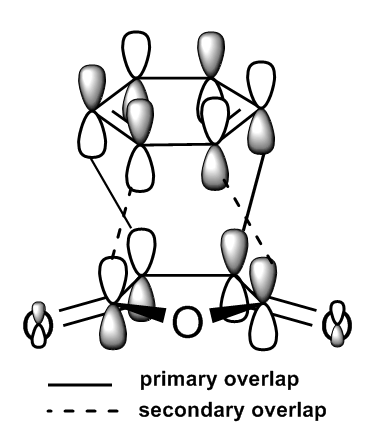
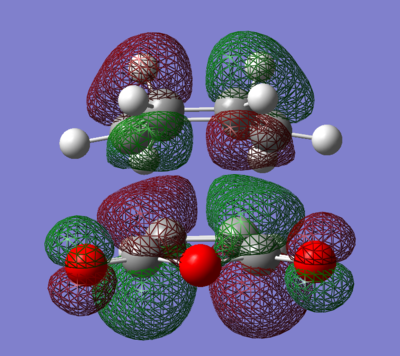
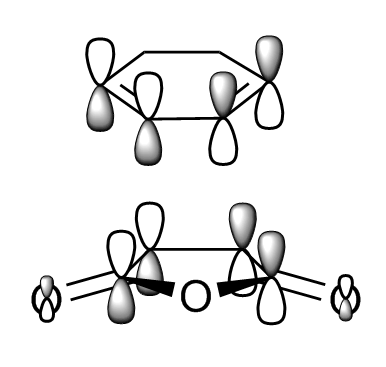
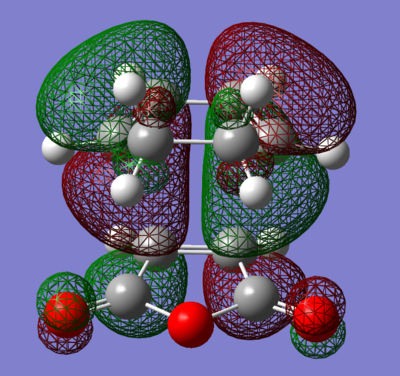
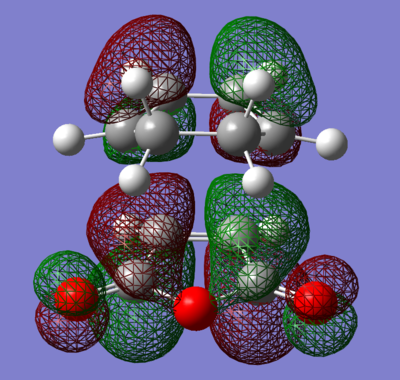
Both transition states were successfully optimised and this can be reflected from the fact that partially formed sigma C-C bond (Endo: C3-C11 and C2-C9; Exo: C3-C9 and C2-C7) have equal bond lengths. Imaginary frequencies were also observed for both structure, confirmed once again that optimized TS structure were computed. From the work of A.Arrieta et al , the distances of new formed C-C bonds were calculated at B3LYP/6-31G* basis set and reported (Endo: 2.22 Å and Exo: 2.24 Å ). They are in a good agreement to the computed values in Table 9 above (Endo: C15-C17 ; Exo: C1-C4 ). The HOMO and LUMO of both TS were plotted in Table 10, along with its frontier orbitals orientations. The main structural difference between Endo and Exo TS was the orientation of cyclohexadiene ring to the maleic anhydride. For Endo TS, -CH₂-CH₂- fragment of cyclohexadiene is in opposite side with –(C=O)-O-(C=O)- of maleic anhydride. While for Exo TS, -CH₂-CH₂- fragment of cyclohexadiene is in same side with –(C=O)-O-(C=O)- of maleic anhydride. This indicated that Exo TS associated with a greater steric hinderance, hence more strained. The distances between C15-C20 and C17-C19 for Endo TS and C15-C20 and C17-C19 for Exo TS are the balance of steric hindrance (increases) and orbital overlaps (decrease). In general, the bond length is longer for Exo TS than Endo one. As previously stated, the partial formed bonds had very similar lengths for both TS; this implied that they were not much affected by the larger steric hindrance presented in Exo TS. To concluded, from the steric point of view, Exo adduct is disfavoured in this cycloaddition.

Same as before, linear combination of atomic orbitals (LCAO) method was employed in given a better illustration on how the frontier orbitals overlap in the TS and results the corresponding HOMO and LUMO structures. The results were summarised in below.

Table 10:MO of Endo and Exo Transition state

	ENDO
Basis Set	Semi-empirical/AM1	Frontier orbitals
Structure of HOMO
Symmetry of HOMO	Antisymmetric
Structure of LUMO
Symmetry of LUMO	Antisymmetric
	EXO
Basis Set	Semi-empirical/AM1	Frontier orbitals
Structure of HOMO
Symmetry of HOMO	Antisymmetric
Structure of LUMO
Symmetry of LUMO	Antisymmetric

From the energies of the TS, Endo TS has slightly lower in energy overall, so it is more stable. Therefore Endo adduct is the kinetic product while the Exo adduct is the thermodynamic product. The Endo TS has lower energy due to the presence of secondary orbitals overlaps (the dashed line shown in the figures in the Table 10). The overlaps are non-bonding interactions between frontier orbitals of both reactants. In the case of Endo TS, the π orbitals of the C=O bonds of maleic anhydride overlap with the HOMO of cyclohexadiene. There has no similar interaction presents in the Exo TS due to the new formed double bond away from the C=O bonds. No stabilization can be gained, so Exo TS had slightly higher energy. Based on the steric effect and the Secondary Orbital Overlaps, Endo TS is both energetically favoured.

The vibrational mode of the TS at Semi-empirical/AM1 were shown in the Figure 10, this enabled the new σ bond formations in this reaction to be investigated.

Figure 10: Vibration mode of Endo Transition state (AM1)

It can be seem that the bond was synchronously formed. Compared to the vibrational mode of the cycloaddition between ethene and cis-butadiene, they were quite similar in nature as well.

Figure 11: IR spectrum of Endo Transition state (AM1)

Effect Neglected in Semi-Empirical/AM1 Calculation of Diels Alder TS

AM1 is a semi-empirical method for the calculation of molecular electronic structure in quantum mechanics aspect. It mainly based on Neglect of Differential Diatomic Overlap integral approximation (NDDO), in which the repulsion of atoms at close separation distances was reduced. . From the first part of this investigation, B3LYP/6-31G* theory was found to have good performance for molecular thermodynamic. This is because the effects of polarization are taken into account in this theory. Therefore, it was used in the further calculations of TS for giving more reliable results (see above). The downside for B3LYP/6-31G* theory is the checkpoint files of the TS for both cycloaddition cannot open successfully due to bad data, so no MOs can be plotted. Thereby, the HOMOs and LUMOs shown in above were obtained from AM1 calculation

Short Summaries for Diels-Alder Cycloadditions

Semi-empirical/AM1 theory was used in initial optimisation and followed by B3LYP/6-31G* thoery is a quite good way to give reasonable results. As the outcome of the computation were in good matches with those obtained from experimental. Computational methods can be a good tool in studying and predicting the molecular thermodynamic of Diels-alder cycloaddition reaction. Second orbital overlaps play an important role in determining the outcome of the reaction, but the relative orientation of the frontier orbitals and steric effects also need to be accounted as well.

Future work

• Generating a guess structure for boat TS of the cope rearrangement and see whether the calculation converge using the reactants and products molecules. Also comparing the results to the one obtained from QST2 methods.
• After first IRC calculation, one out of three options was selected in locating the minimum geometry of the product. Time was not sufficient enough to try on the two remained options, and it would be good to carried out in the future. This can be used to confirmed the actual minimum conformer of the cope rearrangement of 1,5-hexadiene is Gauche 2.Options are (1) restart IRC and specify a larger number of points until it reaches a minimum and (2)Redo the IRC and compute the force constant in every step
• The TS of Diels-Alder Reaction were calculated by computing the force constants at the beginning of the calculation. However, the optimsation with the QST2 methods should be carried out and comparing it to computed results in this investigation.
• Using a more advanced theory instead on those used above in the calculation of Diels alder reaction. The example can be B3LYP-gCP-D3/6-31G*, which was demonstrated practical advantages in calculation and showed its higher robustness over standard B3LYP/6-31G* basis set.
• Investigating other Diels Alder cycloadditions, such as with 4-Chloro-2(H)-pyran-2-one. In which, the dieneophile is monosubstitied and electron deficient. Regio and stereo selectivity of the reaction should be studied and see whether they are in line with the experimental results.