Rep:Mod:PHYSICALotr12

Physical Module: Transition states and reactivity

Introduction

This computational exercise explored the Cope Rearrangement for 1,5-hexadiene and the Diels-Alder reactions for both ethene + butadiene and Cyclohexa-1,3-diene + Maleic Anhydride. The purpose of the exercise was to use methods for isolating transition states and to analyse the transition states obtained. Hartree-Fock, Density Functional Theory and Austen-Model 1 methods were used and their characteristics and comparisons are discussed.

Cope Rearrangement

The Cope Rearrangement is an example of the [3,3]-sigmatropic reaction of 1,5-hexadiene and a _π2 + _σ2 + _π2 cycloaddition. With 6 electrons participating in the mechanism, it is a 4n+2 process and under thermal conditions is suprafacial.

The objective of this exercise was to obtain optimised chair and boat conformers by using various methods to optimise a transition structure, determining advantages and disadvantages ad hoc. The minimum energy path was visualised using the intrinsic reaction coordinate method and different methods of computing the IRC were explored measuring efficiency against time detriment. activation energies found for the cope rearrangement progressing through both a boat and a chair transition state. The activation energies determined in calculation were compared to experimental data.

Figure 1: A mechanism for the Cope Rearrangement

Figure 2: The Chair and Boat Conformer

The lowest energy conformer for 1,5-hexadiene

1,5-hexadiene has 3 carbon-carbon bonds that can rotate. Each of these bonds (highlighted in figure 3) has 3 rotational minima and therefore there are a total of 27 possible structures (3 x 3²). However, due to symmetry and some enantiomers, 17 of these conformers are degenerate leaving 10 conformers of distinct energies.

Figure 3: The bonds available to freely rotate

Initially, a gauche (60^o) and an antiperiplanar (180^o) conformation were built using Gaussview and optimised under HF with a 3-21G basis set. To determine the point groups, a further optimisation with the same theory was undertaken after symmetrisation. These structures were compared with the optimised conformations found in appendix 1 [1].

Table 1: Optimised structures for 'Anti' and 'Gauche' conformations

Anti	Gauche
Optimised Anti Structure	Optimised Gauche Structure
Total Energy = -231.69260237 Hartree	Total Energy = -231.69153035 Hartree
Point Group = C2	Point Group = C2

Table 2: The optimised anti conformations

Anti1	Anti2	Anti3	Anti4
anti1	anti2	anti3	anti4
Total Energy = -231.69260232 Hartree	Total Energy = -231.69253520 Hartree	Total Energy = -231.68907046 Hartree	Total Energy = -231.69097055 Hartree
Point Group = C2	Point Group = CI	Point Group = C2h	Point Group = C1

Table 3: The optimised gauche conformations

Gauche1	Gauche2	Gauche3	Gauche4	Gauche5	Gauche6
gauche1	gauche2	gauche3	gauche4	gauche5	gauche6
Total Energy = -231.68771608 Hartree	Total Energy = -231.69166702 Hartree	Total Energy = -231.69266122 Hartree	Total Energy = -231.69153033 Hartree	Total Energy = -231.68961576 Hartree	Total Energy = -231.68916020 Hartree
Point Group = C2	Point Group = C2	Point Group = C1	Point Group = C2	Point Group = C1	Point Group = C1

Comparing the structures optimised and displayed in table 1 to the structures optimised and displayed in tables 2 and 3, the structures have anti1 and gauche4 conformations.

Looking at the optimised gauche and anti structures, it is expected the anti linkage to have the lower energy due to sterics. However, using the data calculated in tables 2 and 3, it can clearly be seen that the lowest energy conformer for the 1,5-hexadiene is the gauche3 conformer. This agrees with theory that there should be a favourable pi orbital interaction between the terminal double bonds providing a greater contribution to stabilisation than the σ(C-H)/σ*(C-H) interaction in the anti conformation.

A Hartree-Fock optimisation with the 3-21G basis set is a great way to obtain an optimised structure very quickly. In terms of accuracy, there are certainly better methods, but for its calculation speed, it is useful to use.

Density Functional Theory and the anti2 frequency calculation

Density functional theory or DFT assumes a 1:1 mapping between ground state wavefunction and the density functional and is higher level than Hartree-Fock. B3LYP, the DFT functional used in this exercise, combines generalised gradient approximation functionals and Hartree-Fock exchange with a non-elaborate correlation . The method of using terms within Hartree-Fock with 'added extras' allows DFT to be used to obtain a more accurate result to the detriment of time. A opt+freq calculation using DFT with a 6-31G* was used to determine thermochemical values for the anti2 conformation. The asterisk ensured a linear combination between p orbitals and d orbitals allowing for the p orbitals to be polarised. The anti2 conformation had already been optimised and is displayed in table 2. This optimisation produced an energy of -234.61170273 and point group CI. Performing the optimisation with DFT instead of HF has not changed the geometry significantly but the energy is significantly different. This is purely a product of the DFT calculational accuracy. The frequency calculation generated an IR spectrum purely showing peaks in positive wavenumbers.

Figure 4: The IR spectrum of the anti2 conformation

Table 4: Thermochemical values for the anti2 conformation at 298K

Sum of electronic and zero-point Energies	-234.469212 Hartree
Sum of electronic and thermal Energies	-234.461856 Hartree
Sum of electronic and thermal Enthalpies	-234.460912 Hartree
Sum of electronic and thermal Free Energies	-234.500822 Hartree

These energies were calculated at 0K to determine the zero-point energy of the anti2 conformation. This was performed using the temperature keyword at 0.01K.

Table 5: Thermochemical values for the anti2 conformation at 0K

Sum of electronic and zero-point Energies	-234.469212 Hartree
Sum of electronic and thermal Energies	-234.469211 Hartree
Sum of electronic and thermal Enthalpies	-234.469211 Hartree
Sum of electronic and thermal Free Energies	-234.469211 Hartree

At this temperature it can be assumed that there are no thermal contributions to the energy of the structure therefore the total electronic energy of the anti2 structure is -234.469211 Hartree. Comparing this to the sum of electronic and zero-point energies yields that the zero-point energy is 1E-6 Hartree. It is also to be noted that the sum of zero-point and electronic energies should not change with temperature and it is confirmed that it doesn't.

Density functional theory, to compare to the previously discussed Hartree-Fock, is a slower calculation, however, it is more accurate with its results. It is used most frequently in this report for calculating frequencies.

Optimising the Chair Conformation (TS Isolation via Berny Algorithm and Frozen Coordinate)

An allyl fragment was built, optimised with the HF level of theory with a 3-21G basis set and oriented with another allyl fragment to give a guess boat conformer. This was optimised to a transition state (using the opt=noeigen keyword) using the Berny algorithm (HF/3-21G) making a guess of the Hessian and iterating with respect to first derivatives. In layman's terms, the base of the potential maximum is found and then the molecule optimised to the transition state (2-step process for greater accuracy).

Table 6: Optimising the chair conformation using the frozen coordinate method

Anti	Gauche	Imaginary Vibration
Chair Guess Structure	Optimised Chair to Transition State

The imaginary frequency was found to be -817.99 cm^-1 and thus the chair transition structure has been located.

A frozen coordinate method was now used to gain the same result. The advantage of the frozen coordinate method is its more robust but as always, might take slightly longer to prepare than the usual optimisation to a TS via Berny algorithm.

At first, the structure, with bonds being broken/made frozen to 2.2A, was optimised to a minimum using HF and a 3-21G basis set. The product, with bonds unfrozen and specified 'derivative' redundant coordinate method, was optimised to a transition state via the Berny algorithm but with no force constants calculated. The imaginary frequency was found to be -818.08 cm^-1 and so the Berny algorithm and the frozen coordinate method are in agreement.

Optimising the Boat Conformation (QST2)

QST2 was now used to find an average structure between a reactant and product. This average, theoretically, should be the transition state, but this method requires atomic labeling. The atomic labeling used is shown in table 7.

Table 7: Labelled reactant and product

Reactant	Product

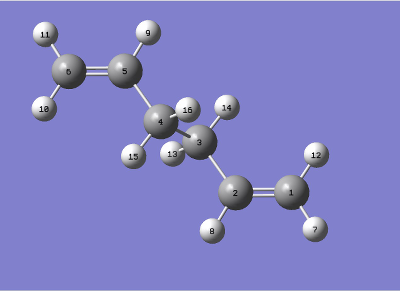
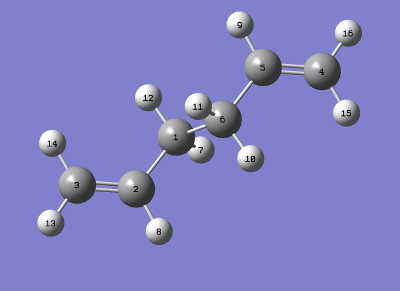
After labeling the reactants and products so the labeling reflects the mechanism, an opt+freq calculation was performed and resulted in a chair-like conformation with an imaginary frequency at -565.77 cm^-1.

Table 8: Chair-like conformation- failed QST2 calc

Chair-like conformation- failed QST2 calc

The calculation failed because the reactant and product were not in the required conformation. The conformations were now changed tending to a boat like conformer (more gauche-like). This was achieved by making the central dihedral angle (c1-c2-c3-c4) 0 ^o and the inside (c2-c3-c4, c3-c4-c5)angles 100 ^o. QST2 cannot rotate bonds, severely limiting its capacity to find accurate transition structures on situation.

Table 9: Labelled reactant and product used in the successful QST2 boat calculation

Reactant	Product

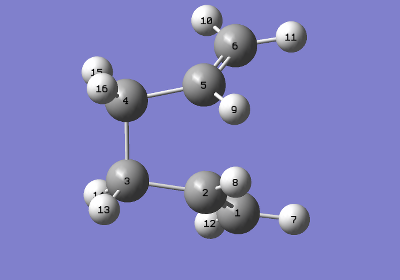
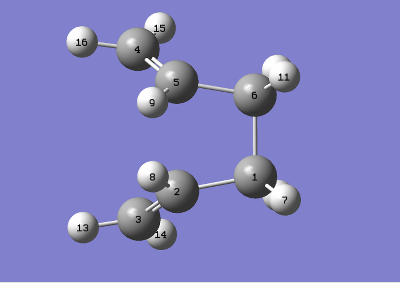
A QST2 calculation was performed on the structures shown in table 9 successfully obtaining the boat transition structure with imaginary vibrational frequency -529.92 cm^-1.

Table 10: The successful QST2 calculation

The boat conformation
The Boat Conformation

Intrinsic Reaction Coordinate Method

After calculating the boat transition structure using QST2, it was evident that the anti-like conformation produced the chair and the gauche-like conformation subsequently produced the boat. However, this is a correlation based on a single calculation and would require further evidence. Furthermore, with the multitude of reaction paths that could in theory be followed after transition state, predicting that a single conformer will be produced from the transition state, would be unscientific. The Intrinsic Reaction Coordinate Method was used to follow the minimum energy path in the forward direction. Force constants were calculated always to ensure the calculation converges and HF/3-21G method used.

Figure 5: Total energy as a function of reaction coordinate

Table 11: The IRC for the chair transition state

IRC Chair transition state

Table 12: A comparison between the final structure generated by the IRC method and the structure generated on optimising (HF, 3-21G) the final structure computed with the IRC method.

IRC Generated Structure	Optimised IRC Generated Structure
IRC Generated Structure	Optimised IRC Generated Structure
Total Energy = -231.69507766 Hartree	Total Energy = -231.69513237 Hartree
Point Group = C1	Point Group = C2

Another IRC was performed on the boat conformer to predict the likely reactant/product types to form or to be formed after the transition structure. It was shown that the structure forms a syn eclipsed product.

Figure 6: Total energy as a function of reaction coordinate

Table 13: The IRC for the boat transition state

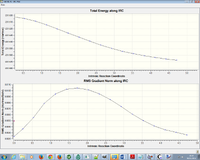
IRC Boat transition state

The product produced from the boat transition state was optimised with low level theory (HF, 3-21G) and the energy reported.

Table 14: The optimisation of the boat IRC

Optimised IRC Generated Structure
IRC Generated Structure	Optimised IRC Generated Structure
Total Energy = -231.66781548 Hartree	Total Energy = -231.68302539 Hartree

It is to be noted that the energy after optimisation for the boat IRC product exhibits a higher difference than calculated in the Chair IRC calculation. This is due to more calculated points in the chair conformation IRC than in the boat conformation IRC. A further IRC of this boat structure should in theory be run with more points calculated for a more accurate result. Secondly, the product produced by the chair is 7.60 kcal/mol thermodynamically more favourable than the product formed after the boat transition state.

Calculating the activation energy of the reaction through both transition structures

Activation energy is the energy required to convert a reactant into a product. The energy profile for the Cope Rearrangement of 1,5-hexadiene is shown in figure 7 and shows how the reactants and products are degenerate. This is not necessarily true and requires details of the mechanism- the reactant and product may be different! For the case of simplicity, it will be assumed that these are equal.

Figure 7: Activation Energy plotted as a function of reaction coordinate for the Cope Rearrangement

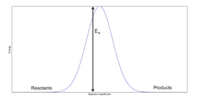
To determine the activation energies for reaction progression through both the boat and the chair transition states, an opt+freq calculation was performed using both HF/3-21G and DFT (B3LYP)/6-31G* methods.

Table 15: Comparison of Energies

	HF/3-21G			B3LYP/6-31G(d)
	Electronic energy	Sum of zero-point and electronic energies	Sum of thermal and electronic energies	Electronic energy	Sum of zero-point and electronic energies	Sum of thermal and electronic energies
		0 K	298.15 K		0 K	298.15 K
Chair TS	-231.61932187	-231.466715	-231.461355	-234.55698284	-234.414924	-234.409004
Boat TS	-231.60280218	-231.450934	-231.445305	-234.54309298	-234.402345	-234.396009
Reactant (anti2)	-231.69024114	-231.532055	-231.532055	-234.61170273	-234.469212	-234.461856

• 1 hartree = 627.509 kcal/mol

Table 16: Activation Energies

	HF/3-21G		B3LYP/6-31G(d)		Deviation from Expt. [[2]]
	0 K	298.15 K	0 K	298.15 K	0 K
Chair ΔE	41.00143806	44.3648863	34.06620859	33.16510567	1.66%
Boat ΔE	50.90415759	54.43640575	41.9596443	41.31958512	5.71%

The activation energies were highly similar to those provided in literature. The energies calculated by both Hartree Fock and Density Functional Theory were significantly different, with density functional theory predicting lower energies. Additionally, the chair is 10.37 kcal/mol lower in energy than the boat conformation concluding that this is the more favourable transition state.

Diels-Alder

The Diels-Alder reaction is a type of _π4_s + _π2_s - pericyclic cycloaddition and is thus a concerted mechanism. One π component will be electron rich and this is usually situated on the diene for a normal electron demand mechanism. The other reacting species will be electron poor for a normal electron demand mechanism. To obtain best HOMO-LUMO overlap, it is beneficial for an electron donating group to be placed in order to raise the HOMO energy and an electron withdrawing group placed in order to lower the LUMO energy.
It is stereoselective with the possibility of diastereomers in the products. Only two diastereomers can form due to strain constraints and these are labelled the EXO and ENDO products. The EXO product is the thermodynamic product however, the ENDO product is the formed fastest due to secondary orbital interactions and is thus kinetic.

Figure 8: An MO diagram for ethylene+butadiene

Ethene + Butadiene

This is an elaborately studied mechanism being the precursor for many more reactions. It is generally agreed that this is a synchronous, concerted mechanism however, there is some interest into a biradical mechanism which is asynchronous. Both of the π orbitals must have equally optimal overlap with the π orbitals of buta-1,3-diene and thus the structure of the transition state is 'envelope', to maximise these interactions.

Optimisation of cis-butadiene using the AM1 semi-empirical method

The AM1 semi-empirical method uses the neglect of diatomic differential overlap, an assumption replacing the overlap matrix with the identity. This makes calculating secular equations simple and quicker.

Cis-butadiene was built and optimised using AM1. The HOMO and LUMO were plotted and are shown in table 17. It can be seen for butadiene that the HOMO is antisymmetrical with regards to the plane of symmetry whereas the LUMO is symmetrical. Ethene was also optimised AM1 and the HOMO/LUMO plotted showed that its HOMO is symmetrical and the LUMO is antisymmetrical.

Table 17: HOMO/LUMO for ethene/cis-buta-1,3-diene

	HOMO	LUMO
ethene
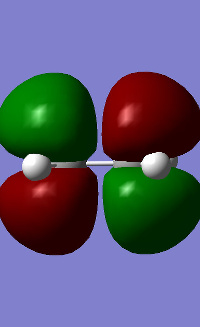
cis-buta-1,3-diene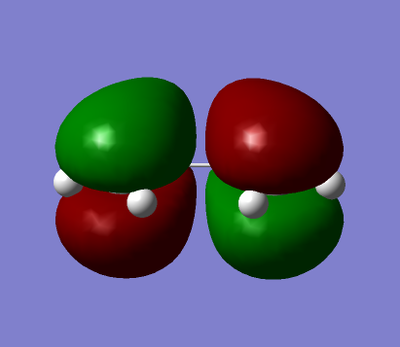

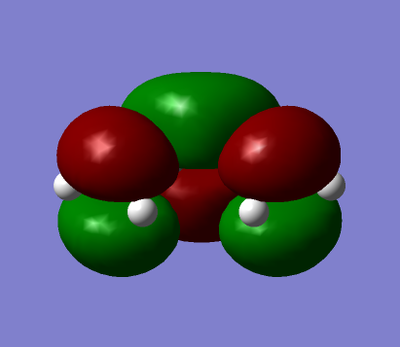
Finding the envelope transition state for the Diels-Alder between ethene and butadiene

The envelope structure was determined by building a guess structure and optimising the structure to a transition state via the Berny algorithm (DFT/6-21G(d)). The guess structure was formed by building a bicyclo structure and erasing the bridge.

On initial optimisation, an envelope structure was obtained, however, with an imaginary frequency of 27.95 cm^-1. This vibrational animation did not reflect the partially formed bonds between the ethene and the butadiene.

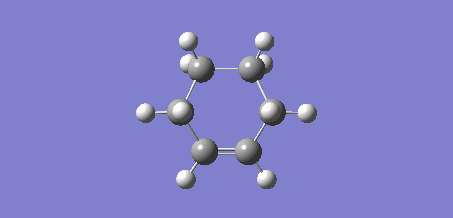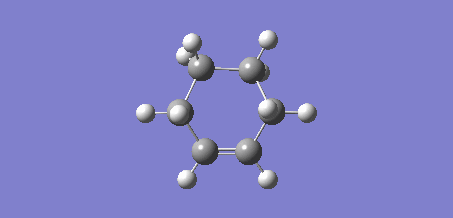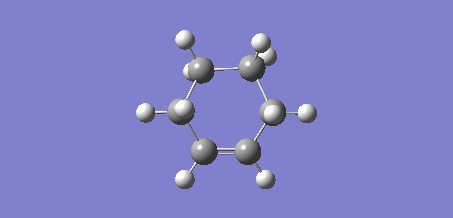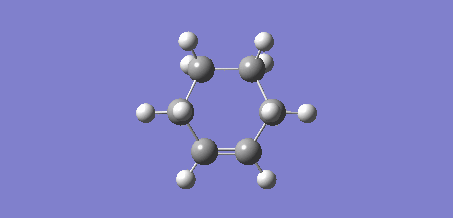
Figure 9: Envelope Structure Obtained on Initial Calculation

Figure 10: Incorrect Vibration

Due to the Berny algorithm converging on an incorrect transition state, the frozen coordinate method was used to determine the transition state. The previously optimised structures of ethene and cis-butadiene were positioned adjacent such that the ethene and butadiene were in a plane. The newly forming bonds between the ethene and the buta-1,3-diene were frozen to 2.0Å and the structure optimised to a minimum using the AM1 method. The AM1 method was used to remain consistent with the ethene and butadiene optimisations computed previously. After optimising the structure to a minimum, the bonds were set to derivative and the structure optimised to a transition state via the Berny algorithm, again under the AM1 method. Like the precursor reaction discussed previously, this Diels-Alder reaction is synchronous .

Table 18: Correct envelope structure obtained with HF/3-21G

Correct envelope structure	Vibration
Figure 9: Correct Envelope Structure Obtained with HF/3-21G

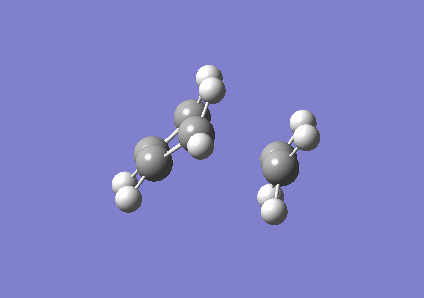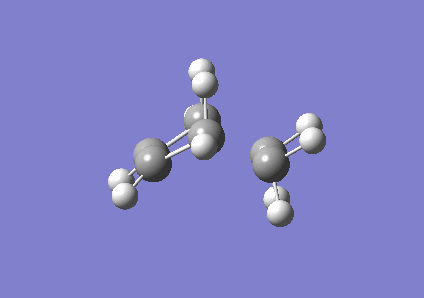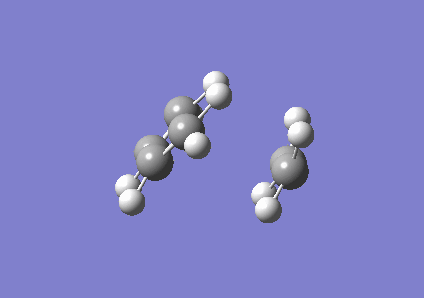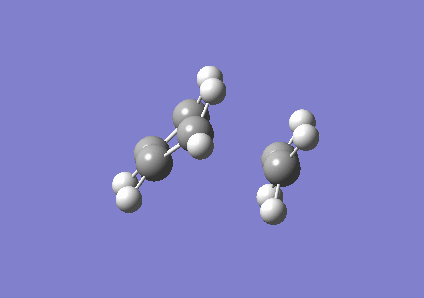
The imaginary frequency found here was -818.99 cm^-1.

Figure 11: An MO diagram for ethylene+butadiene

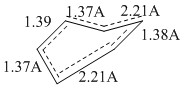
When comparing the original ethene double bond and the newly forming double bond, these were equal in magnitude. This is in line with the synchronous nature of the reaction. While the double bond on the butadiene forms a pi bond, simultaneously, the double bond on the ethene undergoes pi bond cleavage. The newly forming σ bonds were found to be 2.21Å. The typical single bond C-C bond lengths are stated in literature to be 1.54Å and double bond lengths C=C are stated to be 1.34Å . This implies that the σ bonds hadn't yet fully formed. The Van Der Waals radius is stated in literature to be 1.7Å- twice this should be the distance at which non-covalent bonding begins. The newly forming bonds are certainly not 3.4Å and thus there is partial covalent character.

Ethene + butadiene is a symmetry allowed reaction!

Figure 12: An MO frontier orbital diagram for ethylene+butadiene

Table 19: The Woodward-Hoffmann Rules

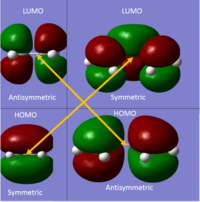
	4n+2	4n
Δ	Suprafacial	Antarafacial
hν	Antarafacial	Suprafacial

A 'symmetry allowed' reaction is one in which there is no change in symmetry between interacting HOMOs or LUMOs. It is the basis for defining whether a pericyclic reaction is allowed or forbidden and furthermore, was the basis for the Woodward-Hoffmann rules. The Woodward-Hoffmann rules are fundamental to the study of pericyclic chemistry and form a simple set of rules. In the case of ethene + butadiene, the HOMO/LUMO on the different reactants are symmetry allowed and thus this is a successful reaction.

Calculating the activation energy of the reaction through the envelope transition structure

DFT/6-31G(d) method was used to perform opt+freq calculations on both the individual reactants, here ethene and butadiene, and the envelope transition structure. The derivative optimisation was repeated with DFT/6-31G(d) to ensure consistency. The thermochemistry has been reported for all of these structures.

Table 20: Comparison of Energies

	DFT/6-31G(d)
	Electronic energy	Sum of thermal and electronic energies
Ethene	-78.59380759	-78.539641
Butadiene	-155.98594957	-155.896785
Combined Ethene + Butadiene	-234.5797572	-234.436426
Envelope	-234.54388562	-234.396907

• 1 hartree = 627.509 kcal/mol

Table 21: Activation Energies

	B3LYP/6-31G(d)
Envelope ΔE	24.79853 kcal/mol

This activation energy compares well with literature with the literature value being between 22.8 and 23.770 at measured at 0K and 500K respectively.

Isolating the EXO/ENDO transition structures for the reaction between maleic anhydride and cyclohexa-1,3-diene

Cyclohexa-1,3-diene and maleic anhydride react via a Diels-Alder reaction to create a cyclohexa-1,3-diene–maleic anyhydride cycloadduct. This reaction is a particularly successful normal electron demand Diels-Alder reaction with the electron withdrawing carbonyl groups of the maleic anhydride lowering the energy of the LUMO. This increases the overlap between the HOMO and the LUMO thus increasing the effectiveness of the Diels-Alder reaction.

As discussed previously, there are two transition states for the Diels-Alder (EXO and ENDO). The ENDO is kinetically fastest formed due to secondary orbital overlap, however, due to the suprafacial nature of the reaction, the geometry of both the diene and the dienophile is conserved in the product and thus the ENDO is more sterically hindered than the EXO product. This is reflected in ENDO being less thermodynamically stable than EXO.

Figure 13: A schematic showing the secondary orbital overlap in the EXO transition state

Figure 14: A schematic showing ENDO transition state

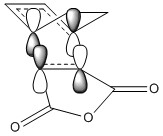
The frozen coordinate method was used here due to QST2(/QST3 might be more effective!) having too many degrees of freedom to push the reactants to react together. It is challenging optimising conditions such as reaction trajectories ensuring reactants form the required transition state. There was also tendency for the ENDO to optimise to the EXO, therefore, a frozen coordinate method, locking the geometry before optimising to the transition state was used.

The EXO transition state was computed initially. The optimised reactants were positioned as shown in figure 13, one above the other. The forming bonds were frozen to 2.2Å and optimised to a minimum using the AM1 semi-empirical method. This was to parameterise the transition structures against experimental data in order to obtain an accurate result. After the structure was optimised to a minimum, the checkpoint file was used to set the forming bonds to derivative and the structure was now optimised to a TS via the Berny algorithm. Force constants were not calculated and again the AM1 semi-empirical method was used.

Table 22: The EXO transition state

EXO	Transition State Vibration
The EXO transition state

This produced an imaginary frequency of 811.86 cm^-1. The vibrational mode was shown to be along the forming bonds and thus the correct transition state was found.

This was repeated with DFT/6-31G(d) method and found an imaginary frequency at 448.49 cm^-1. These imaginary frequencies are remarkably different. The animations produced the same result and thus DFT/6-31G(d) basis set was used for subsequent transition states analyses.

The ENDO transition state was also computed using the frozen coordinate method. The forming bonds were fixed to 2.2Å and DFT/6-31G* basis set used.

Table 23: The ENDO transition state

ENDO	Transition State Vibration
The ENDO transition state

This showed a transition state vibration at -447.21 cm^-1

The HOMO and LUMO for both the ENDO and EXO structures were plotted.

Table 24: HOMO/LUMO for ENDO/EXO

	HOMO	LUMO
ENDO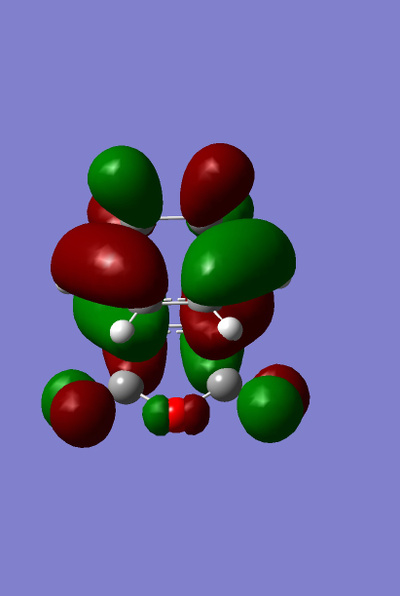
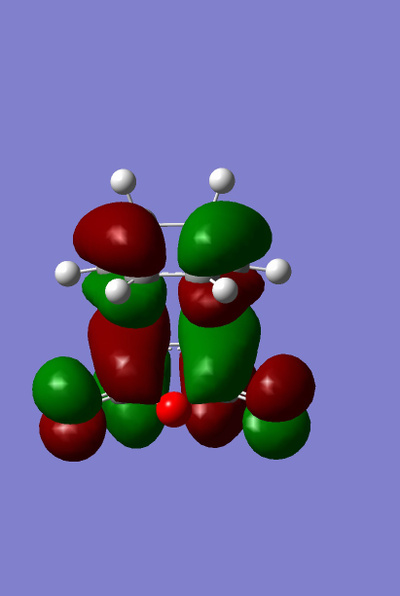
EXO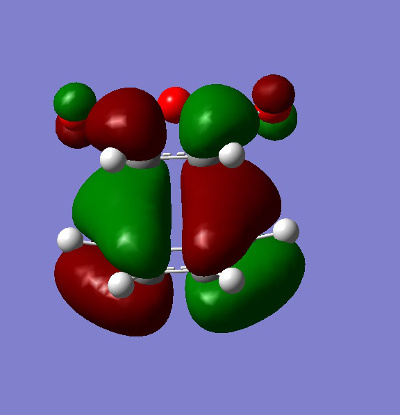

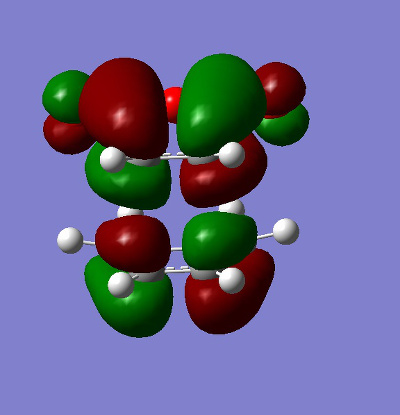
It can be clearly seen that these molecular orbitals are all antisymmetric with regards to the plane and thus this is a symmetry allowed reaction (discussed later).

IRC analysis of the ENDO and EXO transition states

An IRC analysis was undertaken to model the reaction coordinate and analyse the thermodynamics.

The ENDO IRC was conducted first, calculated in the forward direaction using HF/3-21G method.

Figure 15: Total energy as a function of reaction coordinate vs RMS along IRC against reaction coordinate

Table 25: The IRC for the EXO transition state

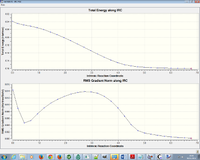
IRC EXO transition state

Figure 16: Total energy as a function of reaction coordinate vs RMS along IRC against reaction coordinate

Table 26: The IRC for the ENDO transition state

IRC ENDO transition state

The final structure files in these IRC calculations were optimised to compare the electronic energies of the product, providing further insight into the thermodynamic/kinetic products of this reaction.

Table 27: An energy comparison between the product structure produced from the EXO and ENDO transition states

EXO	ENDO
EXO optimised IRC structure	ENDO optimised IRC structure
Total Energy = -605.72132064 Hartree	Total Energy = -605.71873538 Hartree

It can be seen that the EXO product is 1.6223 kcal/mol more stable than the ENDO product and thus this is the thermodynamic product.

Energetic Analysis of the ENDO/EXO transition structures and activation energy calculation

Table 28: Electronic Energy of the ENDO/EXO transition structures (DFT 6-31G(d))

ENDO TS	EXO TS
612.68339632 Hartree	-612.67931093 Hartree

From the data gathered it is evident that the ENDO transition state is lower in energy than the EXO transition state further supporting the idea it is the first formed. In terms of the thermodyamics, it is expected that the product, after the EXO transition state, is lower in energy than the product formed after the ENDO transition state.

Activation energies were calculated by again performing opt+freq calculations on the individual reactants using DFT/6-31G(d). These calculations had already been performed on the ENDO and EXO products and thus did not have to be repeated.

Table 29: Comparison of Energies

	B3LYP/6-31G(d)
	Electronic energy	Sum of thermal and electronic energies
Maleic Anhydride	-379.28954408	-379.228473
Cyclo-1,3-hexadiene	-233.41893619	-231.450934
Combined Maleic Anhydride + Cyclo-1,3-hexadiene	-612.7084803	-610.679407
ENDO	-612.68339632	-612.491780
EXO	-612.67931093	-612.487661

• 1 hartree = 627.509 kcal/mol

Table 30: Activation Energies

	B3LYP/6-31G(d)
EXO ΔE	1137.280369 kcal/mol
ENDO ΔE	1134.695659 kcal/mol

The activation energies calculated seem very high but literature could not be found to confirm. These activation energy calculations definitively prove that the ENDO product has the lower activation energy barrier by 2.58471 kcal/mol. This is, as described before, due to secondary orbital interactions.

Figure 17: A schematic showing the secondary orbital interactions in the ENDO transition state

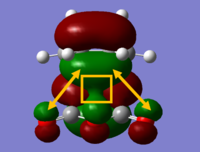
The HOMO-2 orbital was analysed in this case as this was the stabilising interaction. The figure not only highlights the secondary orbital interactions but also conjugation between the reactants shown in the square.

Maleic Anhydride + cyclohexa-1,3-diene is (again!) a symmetry allowed reaction!

Figure 18: An MO frontier orbital diagram for Cyclohexa-1,3-diene and maleic anhydride

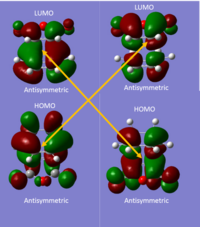
With all frontier orbitals in this reaction possessing antisymmetric reflective planes, this reaction is symmetry allowed and by the Woodward-Hoffmann rules is suprafacial under thermal conditions.

Conclusion

This experiment compared and contrasted various methods for optimising and analysing transition structures, namely the Berny algorithm, the frozen coordinate method, QST2 and IRC showing each to have strong advantages and hindrances in circumstance where another one of these methods is more useful. At first, the Cope Rearrangement was studied, finding the boat and chair transition state conformers. It was found that the chair transition structure was kinetically favoured and its product thermodynamically favoured. A Diels-Alder investigation was also undertaken looking into ethene+butadiene and maleic anhydride+cyclo-1,3-hexadiene reactions. It was confirmed that both of these reactions are symmetrically-allowed and the transition states were computed for both reactions and analysed. The endo product, whilst having the computed lower transition state energy than the exo transition state, was higher in energy than the exo product. Rationalising this led to the conclusion that the endo product is kinetically favoured whilst the exo product thermodynamically favoured.

References

<references>