Rep:Mod:PHJ1145

General comments: a good attempt at the lab - you've understood most things but there do appear to be gaps in knowledge. Don't complicate the problem, think of the simple physics (the wonderful thing about classical dynamics is that things generally follow common sense...) Mark: 64/100

Introduction to molecular dynamics simulation

Numerical Integration

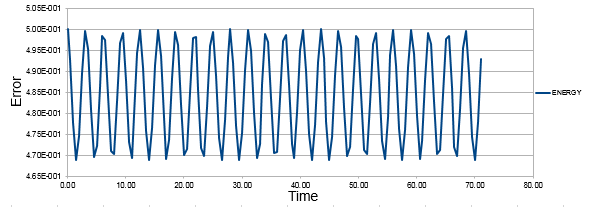
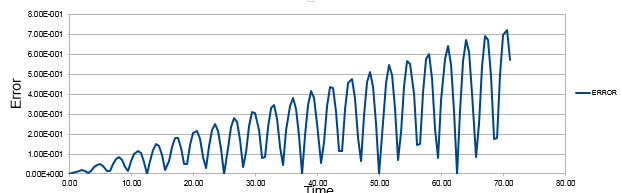
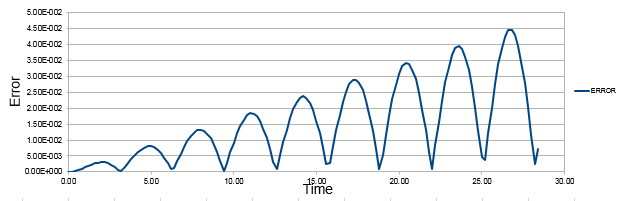
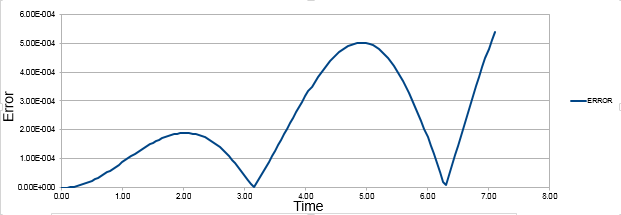
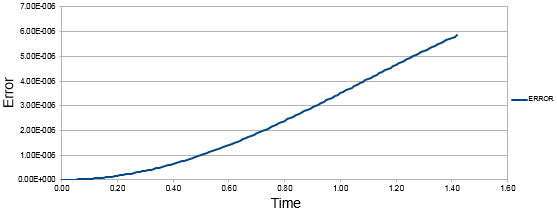
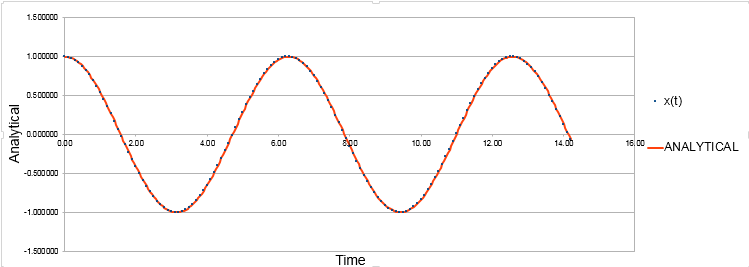
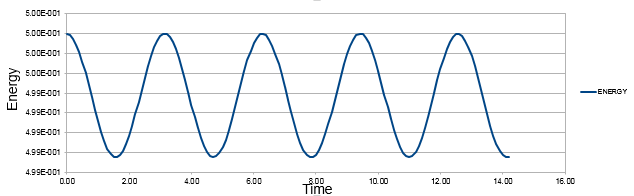
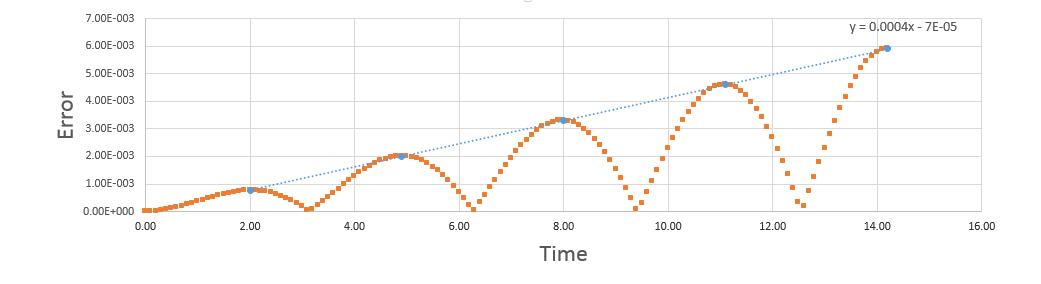
TASK:Complete the three columns "ANALYTICAL", "ERROR", and "ENERGY" "ANALYTICAL" s hould contain the value of the classical solution for the position at time t, "ERROR" should contain the absolute difference between "ANALYTICAL" and the velocity-Verlet solution and "ENERGY" should contain the total energy of the oscillator for the velocity-Verlet solution. Remember that the position of a classical harmonic oscillator is given by $x\left(t\right)=A\cos (\omega t+\varphi )$ For the default timestep value, 0.1, estimate the positions of the maxima in the ERROR column as a function of time. Make a plot showing these values as a function of time, and fit an appropriate function to the data.

Analytical against Time	Energy against Time	Error against Time |-

The position of a classical harmonic oscillator is given by $x\left(t\right)=A\cos (\omega t+\varphi )$
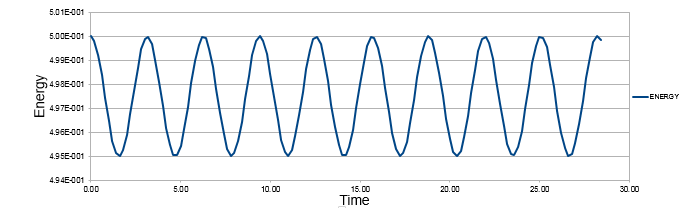
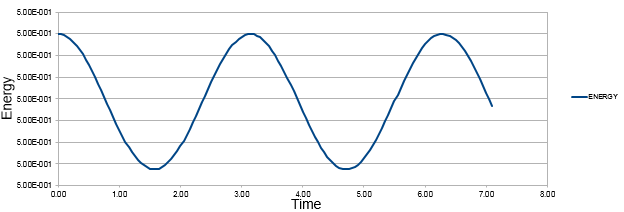
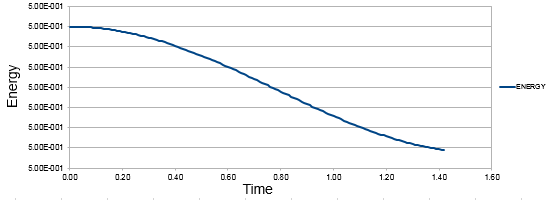
The comparison of classical harmonic oscillator and Velocity -Verlet solution for displacement as a function of time, the total energy with time and the error between the classical harmonic oscillator and Velocity-Verlet solution are shown above. The total energy was calculated by adding kinetic and potential energies. $E=0.5m{v}^2+0.5k{x}^2$
Where x is the displacement from the equilibrium distance, m is the mass which was 1 and velocity-Verlet algorithm was used for the velocity values. As the time increases the error between the classical harmonic solution and the velocity-Verlet solution increases which is shown by the linear plot of the maxima points of error.

TASK: Experiment with different values of the timestep. What sort of a timestep do you need to use to ensure that the total energy does not change by more than 1% over the course of your "simulation"? Why do you think it is important to monitor the total energy of a physical system when modelling its behaviour numerically?

Timestep 0.50	Timestep 0.20	Timestep 0.05	Timestep 0.01
Energy for timestep 0.5	Energy for timestep 0.2	Energy for timestep 0.05	Energy for timestep 0.01
Error for timestep 0.5	Error for timestep 0.2	Error for timestep 0.05	Error for timestep 0.01

As the timestep increases the error also increases. By using trial and error method timestep = 0.2 was obtained which does not change the total energy by more than 1 % over the course of the simulation. The timestep below 0.2 are suitable to use however larger timestep is better as the system can be ran for the larger period of time. Tick The total energy of a physical system needs to be monitored as it shows whether the system has reached equilibrium. If the system does not reach equilibrium, the system is not suitable to use for the simulation. And also the total energy can be monitored to see if it obeys to the law of conservation of energy.Tick

Atomic Forces

TASK: For a single Lennard-Jones interaction, $\varphi \left(r\right)=4ϵ(\frac{{\sigma }^{12}}{r^{12}}-\frac{{\sigma }^6}{r^6})$, find the separation, $r_0$, at which the potential energy is zero. What is the force at this separation? Find the equilibrium separation, $r_{eq}$, and work out the well depth ($\varphi \left(r_{eq}\right)$). Evaluate the integrals $\underset{2\sigma }{\overset{\mathrm{\infty }}{\int }}\varphi \left(r\right)\mathrm{d}r$, $\underset{2.5\sigma }{\overset{\mathrm{\infty }}{\int }}\varphi \left(r\right)\mathrm{d}r$, and $\underset{3\sigma }{\overset{\mathrm{\infty }}{\int }}\varphi \left(r\right)\mathrm{d}r$ when $\sigma =ϵ=1.0$.

The separation at which the potential energy is zero

Force at which potential is zero

$r_0$ = $\sigma$ $\varphi \left(r_0\right)=4ϵ(\frac{{\sigma }^{12}}{r^{12}}-\frac{{\sigma }^6}{r^6})$ $0=4ϵ(\frac{{\sigma }^{12}}{r^{12}}-\frac{{\sigma }^6}{r^6})$ $0=(\frac{{\sigma }^{12}}{r^{12}})-(\frac{{\sigma }^6}{r^6})$ $(\frac{{\sigma }^{12}}{r^{12}})=(\frac{{\sigma }^6}{r^6})$ $(\frac{1}{r^6})=(\frac{1}{{\sigma }^6})$ $r_0=\sigma$ Tick OR $r_0=\mathrm{\infty }$ This isn't r_0 though, this is dissoc en. But yes, the potential is 0 at infinite separation..

$\mathbf{F}$ when $r_0$ $\mathbf{F}=-\frac{\mathrm{d}U\left({\mathbf{r}}_0\right)}{\mathrm{d}{\mathbf{r}}_i}$ $\varphi \left(r_0\right)=4ϵ(\frac{{\sigma }^{12}}{r^{12}}-\frac{{\sigma }^6}{r^6})$ $-\frac{\mathrm{d}U\left({\mathbf{r}}_0\right)}{\mathrm{d}{\mathbf{r}}_i}=-4ϵ(\frac{-12{\sigma }^{12}}{r^{13}}+\frac{6{\sigma }^6}{r^7})$ $r_0=\sigma$ $=-4ϵ(\frac{-12}{\sigma }+\frac{6}{\sigma })$ $=-\frac{-24ϵ}{\sigma }$ $=\frac{24ϵ}{\sigma }$ Tick

The equilibrium separation	The well depth
$r_{eq}$ $r_{eq}$ is when the potential energy is the minimum $r_{eq}=-\frac{\mathrm{d}U\left(\mathbf{r}\right)}{\mathrm{d}\mathbf{r}}=0$ $-\frac{\mathrm{d}U\left(\mathbf{r}\right)}{\mathrm{d}\mathbf{r}}=24ϵ(\frac{2{\sigma }^{12}}{r^{13}}-\frac{{\sigma }^6}{r^7})$ $(\frac{2{\sigma }^{12}}{r^{13}}=\frac{{\sigma }^6}{r^7})$ $r^6=2{\sigma }^6$ $=2^{1/6}\sigma$ Tick $r_{eq}=2^{1/6}\sigma$	$(\varphi \left(r_{eq}\right))$ Hence, $\varphi \left(r_{eq}\right)=4ϵ(\frac{{\sigma }^{12}}{r_{eq}^{12}}-\frac{{\sigma }^6}{r_{eq}^6})$ $=4ϵ(\frac{{\sigma }^{12}}{(2^{1/6}\sigma {)}^{12}}-\frac{{\sigma }^6}{(2^{1/6}\sigma {)}^6})$ $=4ϵ(\frac{1}{4}-\frac{1}{2})$ $=-ϵ$Tick

Evaluate $\underset{2\sigma }{\overset{\mathrm{\infty }}{\int }}\varphi \left(r\right)\mathrm{d}r$

$\underset{2.5\sigma }{\overset{\mathrm{\infty }}{\int }}\varphi \left(r\right)\mathrm{d}r$

$\underset{3\sigma }{\overset{\mathrm{\infty }}{\int }}\varphi \left(r\right)\mathrm{d}r$ when $\sigma =ϵ=1.0$

$\underset{2\sigma }{\overset{\mathrm{\infty }}{\int }}\varphi \left(r\right)\mathrm{d}r$	$\underset{2.5\sigma }{\overset{\mathrm{\infty }}{\int }}\varphi \left(r\right)\mathrm{d}r$	$\underset{3\sigma }{\overset{\mathrm{\infty }}{\int }}\varphi \left(r\right)\mathrm{d}r$
$\underset{2\sigma }{\overset{\mathrm{\infty }}{\int }}\varphi \left(r\right)\mathrm{d}r$ $\underset{2\sigma }{\overset{\mathrm{\infty }}{\int }}\varphi \left(r\right)\mathrm{d}r=\underset{2\sigma }{\overset{\mathrm{\infty }}{\int }}4ϵ(\frac{{\sigma }^{12}}{r^{12}}-\frac{{\sigma }^6}{r^6})dr$ $\underset{2\sigma }{\overset{\mathrm{\infty }}{\int }}\varphi \left(r\right)\mathrm{d}r=\underset{2\sigma }{\overset{\mathrm{\infty }}{\int }}4ϵ(\frac{{\sigma }^{12}}{r^{12}}-\frac{{\sigma }^6}{r^6})dr$ $=\underset{2\sigma }{\overset{\mathrm{\infty }}{\int }}4ϵ(\frac{{\sigma }^{12}}{r^{12}}-\frac{{\sigma }^6}{r^6})dr$ $=[4ϵ(\frac{{\sigma }^{12}}{-11r^{11}}-\frac{{\sigma }^6}{-5r^5})]{|}_{2\sigma }^{\mathrm{\infty }}$ $=0-4ϵ(\frac{{\sigma }^{12}}{-11(2\sigma {)}^{11}}-\frac{{\sigma }^6}{-5(2\sigma {)}^5})$ $=0-4ϵ(\frac{\sigma }{-22528}-\frac{\sigma }{-160})$ $=-ϵ(\frac{699\sigma }{28160})=-0.0248$Tick	Previous equations were used with substituted $\sigma$. $=0-4ϵ(\frac{{\sigma }^{12}}{-11(2.5\sigma {)}^{11}}-\frac{{\sigma }^6}{-5(2.5\sigma {)}^5})$ $=-0.00818$Tick	Previous equations were used with substituted $\sigma$. $=0-4ϵ(\frac{{\sigma }^{12}}{-11(3\sigma {)}^{11}}-\frac{{\sigma }^6}{-5(3\sigma {)}^5})$ $=-0.00329$Tick

TASK: Estimate the number of water molecules in 1ml of water under standard conditions. Estimate the volume of 10000 water molecules under standard conditions.

1 mL of water = 1 g of water Mr of Water molecule : 18.15 g/mol
1/ 18.15 = 0.0551 mol
$0.0551*6.022*10^{23}$
$=3.427*10^{22}$ $$\begin{gathered} Number \\ of \\ water \\ molecules \\ in \\ 1mL=3.427*10^{22} \end{gathered}$$ Tick

Volume of 10000 water molecules
$10000/3.427*10^{22}$
$$\begin{gathered} =2.918*10^{-19} \\ mL \end{gathered}$$Tick

TASK: Consider an atom at position $(0.5,0.5,0.5)$ in a cubic simulation box which runs from $(0,0,0)$ to $(1,1,1)$. In a single timestep, it moves along the vector $(0.7,0.6,0.2)$. At what point does it end up, after the periodic boundary conditions have been applied?
If we add two vectors to get the final position, we get vector (1.2, 1.1, 0.7). At the periodic boundary conditions,an infinite number of replicas is available for the system and therefore the vector of the final position of atom is (0.2, 0.1, 0.7). Tick

TASK: The Lennard-Jones parameters for argon are $$\begin{gathered} \sigma =0.34\mathrm{n}\mathrm{m},ϵ \\ / \\ {k}_B=120\mathrm{K} \end{gathered}$$. If the LJ cutoff is $r^{*}=3.2$, what is it in real units? What is the well depth in $$\begin{gathered} {\mathrm{k}\mathrm{J} \\ \mathrm{m}\mathrm{o}\mathrm{l}}^{-1} \end{gathered}$$? What is the reduced temperature $T^{*}=1.5$ in real units?

$$\begin{gathered} r=3.2*0.34*10^{-9}=1.088*10^{-9} \\ m=1.088 \\ nm(3d.p) \end{gathered}$$ Tick

$$\begin{gathered} Well \\ depth=\varphi =-ϵ \end{gathered}$$

$$\begin{gathered} =-120*k_B=-997.68J/mol=-0.998 \\ kJ/mol(3d.p) \end{gathered}$$

$$\begin{gathered} T=1.5*120=150 \\ K \end{gathered}$$ Typo, 180

Equilibration

TASK: Why do you think giving atoms random starting coordinates causes problems in simulations? Hint: what happens if two atoms happen to be generated close together?

- Giving atoms random starting coordinates could cause atoms at the same space. This would cause an error in simulation as r tends to 0 resulting Lennard-Jones potential to be infinite. $(\frac{\sigma }{r_{ij}}{)}^6\approx \mathrm{\infty }$ when $r\approx 0$

TASK: Satisfy yourself that this lattice spacing corresponds to a number density of lattice points of 0.8. Consider instead a face-centred cubic lattice with a lattice point number density of 1.2. What is the side length of the cubic unit cell?

$$\begin{gathered} number \\ of \\ density=\frac{Number \\ of \\ atoms}{Lattice \\ Spacin{g}^3} \end{gathered}$$ $$\begin{gathered} number \\ of \\ density=\frac{1}{1.07722^3} \end{gathered}$$ $=0.799994...\approx 0.8$ Tick

The side length for a face-centered cubic lattice with a lattice point number density of 1.2.

$$\begin{gathered} number \\ of \\ density=\frac{Number \\ of \\ atoms}{Lattice \\ Spacin{g}^3} \end{gathered}$$

$$\begin{gathered} 1.2=\frac{4}{Lattice \\ Spacin{g}^3} \end{gathered}$$

$$\begin{gathered} Lattice \\ Spacing=(\frac{4}{1.2}{)}^{1/3}=1.493801...\approx 1.49 \end{gathered}$$Tick

TASK: Consider again the face-centred cubic lattice from the previous task. How many atoms would be created by the create_atoms command if you had defined that lattice instead?
From the previous task, the face centred cubic lattice with density 1.2 has 4 atoms per unit cell and therefore 4000 atoms would be created as the system as 1000 unit cell in total.

TASK: Using the LAMMPS manual, find the purpose of the following commands in the input script:

mass 1 1.0
pair_style lj/cut 3.0
pair_coeff * * 1.0 1.0

 mass 1 1.0 code 

This code is in the form of mass (atom type) (mass). And the code is showing that there is only one atom type associated with the mass of 1.0.

 pair_style lj/cut 3.0 

This code defines the Lenard-Jones interactions of the atoms with the cutoff value 3.0. Cut off distance is needed because if r increases to infinity, Lennard-Jones potential tends to 0.

 pair_coeff * * 1.0 1.0 

This code is in the form of

 pair_coeff (atom type)(atom type) (coefficient)(coefficient) 

This code defines that the coefficients 1.0 apply to all atoms in the system. A wildcard asterisk code defines all the types of atoms in the system. The coefficients 1.0 corresponds sigma and epsilon.

$\sigma =ϵ=1.0$

TASK: Given that we are specifying ${\mathbf{x}}_i\left(0\right)$ and ${\mathbf{v}}_i\left(0\right)$, which integration algorithm are we going to use?
Velocity-Verlet integration algorithm that employs the half-step method can be used as the initial velocity and initial positions are specified.

TASK: Look at the lines below.
Code 1

### SPECIFY TIMESTEP ###
variable timestep equal 0.001
variable n_steps equal floor(100/${timestep})
variable n_steps equal floor(100/0.001)
timestep ${timestep}
timestep 0.001

### RUN SIMULATION ###
run ${n_steps}
run 100000

The second line (starting "variable timestep...") tells LAMMPS that if it encounters the text ${timestep} on a subsequent line, it should replace it by the value given. In this case, the value ${timestep} is always replaced by 0.001. In light of this, what do you think the purpose of these lines is? Why not just write:
Code 2

timestep 0.001
run 100000

The code 2 is not suitable for running with different timestep value.By using the code 1, the timestep value would be calculated automatically and calculated timestep would be used for the run as shown from the last line of the code. Therefore for our experiment using the code 1 is suitable as different timestep values were used. Be more explicit - makes changing the timestep throughout the code easier!

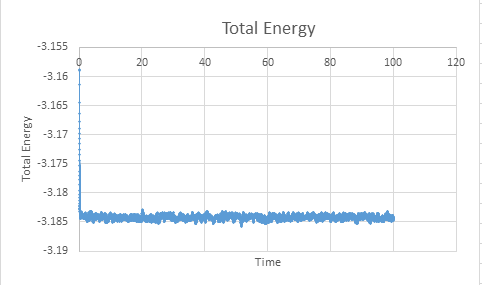
TASK: make plots of the energy, temperature, and pressure, against time for the 0.001 timestep experiment (attach a picture to your report). Does the simulation reach equilibrium? How long does this take? When you have done this, make a single plot which shows the energy versus time for all of the timesteps (again, attach a picture to your report). Choosing a timestep is a balancing act: the shorter the timestep, the more accurately the results of your simulation will reflect the physical reality; short timesteps, however, mean that the same number of simulation steps cover a shorter amount of actual time, and this is very unhelpful if the process you want to study requires observation over a long time. Of the five timesteps that you used, which is the largest to give acceptable results? Which one of the five is a particularly bad choice? Why?

Total energy against timestep 0.001
Temperature against timestep 0.001
Pressure against timestep 0.001

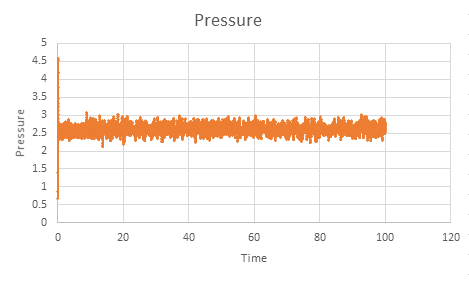The energy, temperature and pressure against time for the 0.001 timestep experiment are shown above. For the timestep 0.001 equilibrium reaches approximately at 0.3 which is very short time.

Energy against different timesteps

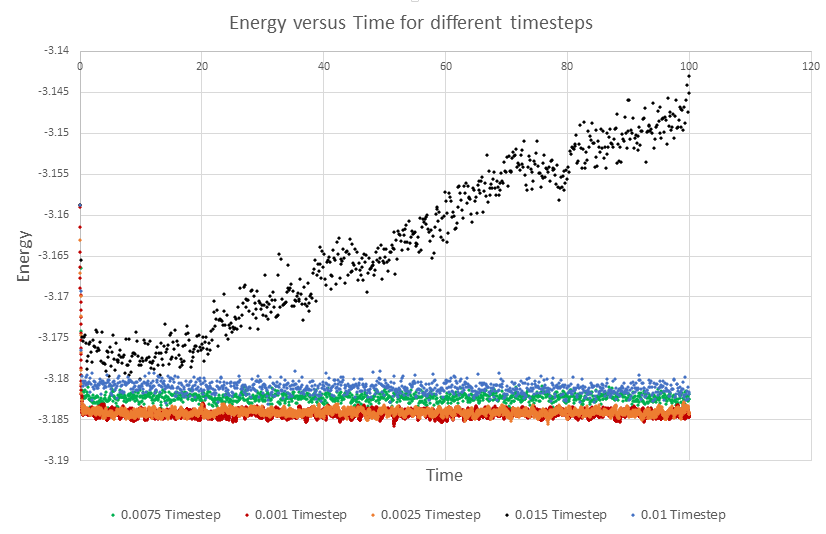
From the graph above the time step 0.015 is not suitable for the experiment as it does not reach equilibrium. For the total energy of 0.01 and 0.0075 decrease slightly with time. And therefore 0.0025 and 0.001 timestep are relatively suitable for the experiment. Even though shorter timesteps would give more accurate result, as it is not suitable for the experiment to study observation over a long time, 0.0025 is the largest to give the acceptable results.Tick

Running simulations under specific conditions

TASK: Choose 5 temperatures , and two pressures. This gives ten phase points — five temperatures at each pressure. Create 10 copies of npt.in, and modify each to run a simulation at one of your chosen \left(p, T\right) points. You should be able to use the results of the previous section to choose a timestep. Submit these ten jobs to the HPC portal.

Temperatures: 1.5, 1.6, 1.7, 1.8, 1.9
Pressures: 2.5, 2.6
Timestep:0.0025

TASK: We need to choose $\gamma$ so that the temperature is correct $T=\mathfrak{𝔗}$ if we multiply every velocity $\gamma$. We can write two equations: $E_K=\frac{3}{2}N{k}_{B}T$ $\frac{1}{2}\sum _i{m}_i{v}_i^2=\frac{3}{2}N{k}_{B}T$ Solve these to determine $\gamma$.

$E_K=\frac{3}{2}N{k}_{B}T$

$\frac{1}{2}\sum _i{m}_i{v}_i^2=\frac{3}{2}N{k}_{B}T$

$$\begin{gathered} \frac{1}{2}\sum _i{m}_i(v_i\gamma {)}^2 \\ =\frac{3}{2}N{k}_B\mathfrak{𝔗} \end{gathered}$$

$$\begin{gathered} {\gamma }^2\sum _i{m}_i{v}_i^2 \\ =3N{k}_B\mathfrak{𝔗} \end{gathered}$$

$$\begin{gathered} \sum _i{m}_i{v}_i^2 \\ =3N{k}_{B}T \end{gathered}$$

${\gamma }^{2}3N{k}_{B}T=3N{k}_B\mathfrak{𝔗}$

${\gamma }^2=\frac{\mathfrak{𝔗}}{T}$

$\gamma =\pm \sqrt{\frac{\mathfrak{𝔗}}{T}}$ Tick

TASK: Use the manual page to find out the importance of the three numbers 100 1000 100000. How often will values of the temperature, etc., be sampled for the average? How many measurements contribute to the average? Looking to the following line, how much time will you simulate?

### MEASURE SYSTEM STATE ###
thermo_style custom step etotal temp press density
variable dens equal density
variable dens2 equal density*density
variable temp equal temp
variable temp2 equal temp*temp
variable press equal press
variable press2 equal press*press
fix aves all ave/time 100 1000 100000 v_dens v_temp v_press v_dens2 v_temp2 v_press2
run 100000

fix aves all ave/time Nevery Nrepeat Nfreq

The purpose of this script is to calculate the average values and the final average values generated on timesteps that are multiples of Nevery, for Nrepeat number of times and an average is generated every Nfreq timesteps.
* 100 (Nevery)is the gap between the timestep values that will be used to calculate the average
* 1000 (Nrepeat) is the number of data point that are used to calculate the averages.
* 100000 (Nfreq) is the number of timesteps used for the calculation of averages.
And therefore the script is saying in every 100 timesteps the value will be used to calculate the averages with 1000 data points. 100000 timesteps will be used to calculate the averages. Tick
For our simulation, 0.0025 was used as a timestep so the number of timesteps used for the calculation of averages is 250.

TASK: When your simulations have finished, download the log files as before. At the end of the log file, LAMMPS will output the values and errors for the pressure, temperature, and density $\left(\frac{N}{V}\right)$. Use software of your choice to plot the density as a function of temperature for both of the pressures that you simulated. Your graph(s) should include error bars in both the x and y directions. You should also include a line corresponding to the density predicted by the ideal gas law at that pressure. Is your simulated density lower or higher? Justify this. Does the discrepancy increase or decrease with pressure?

Density against time

Density against time including density calculated with ideal gas law

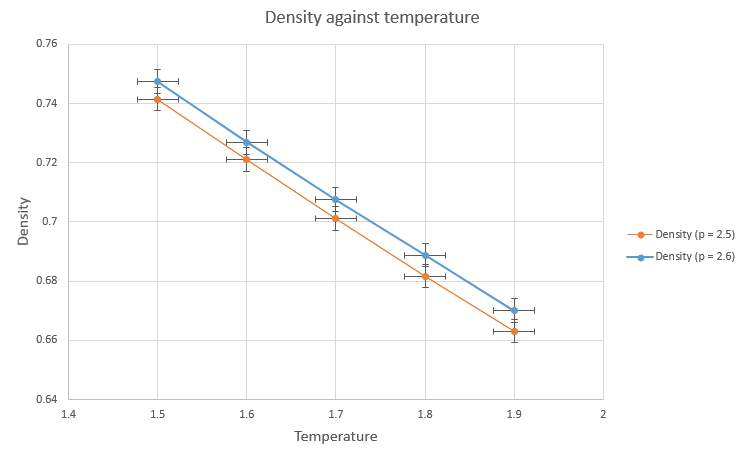
• Above graph shows that as the temperature increases the density decreases. This is because of expansion of volume as particles gets energy.
• As the pressure increases the density increases.
• There is big difference between the densities calculated using ideal gas law and the simulated values. As ideal gas law assumes there is no interaction between atoms where the Lennard-Jones potential takes into account the attractive and repulsive forces. This leads to the much lower density compare to the calculated values using ideal gas law. Tick
• The discrepancy seems decreased as the pressure decreased however more data would be needed to clarify this.

Calculating heat capacities using statistical physics

TASK: As in the last section, you need to run simulations at ten phase points. In this section, we will be in density-temperature $({\rho }^{*},T^{*})$ phase space, rather than pressure-temperature phase space. The two densities required at 0.2 and 0.8, and the temperature range is 2.0, 2.2, 2.4, 2.6, 2.8. Plot $C_V/V$ as a function of temperature, where V is the volume of the simulation cell, for both of your densities (on the same graph). Is the trend the one you would expect? Attach an example of one of your input scripts to your report.


These are the values used to plot the graph.
Temperature ranges: 2.0, 2.2, 2.4, 2.6, 2.8
Densities: 0.2, 0.8
Timestep: 0.0025

Heat capacity/volume against temperature

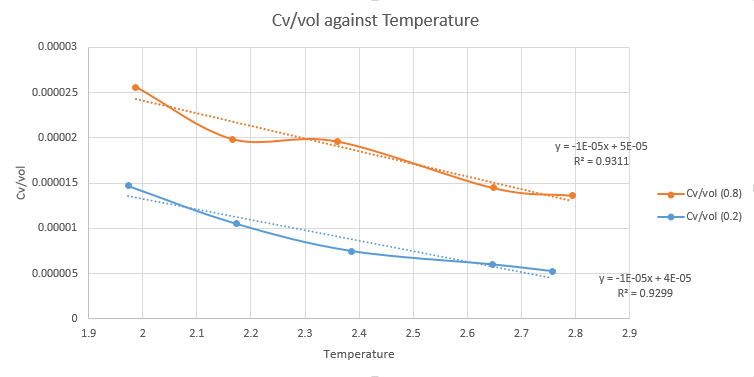
The trend of the above graph is showing as the temperature increases the heat capacity decreases.Which is different to the trend expected by ideal gas law and thermodynamics.

• Ideal gas law: The equipartition theorem shows that the heat capacity equals to 3R/2 meaning the heat capacity is constant and independent to the change in temperature. Tick

$$\begin{gathered} Cv=\frac{3R}{2} \\ (R=gas \\ constant) \end{gathered}$$

• Thermodynamics:The equations below show that, because $\frac{dS}{dT}$ will be positive or equals to 0, if the temperature increases the heat capacity also increases. This isn't true for a monatomic crystal?

$Cv=\frac{dU}{dT}$
$dU=TdS-PdV$
$Cv=T\frac{dS}{dT}-P\frac{dV}{dT}$

This trend could have the similar reason with Schottky anomaly.Not quite.. At high temperature, the system cannot absorb energy anymore because of the increasing internal energy of the system and all the levels are populated. And therefore heat capacity decreases as the entropy changes is smaller where temperature is keep increasing. Also the English here isn't great
Higher density causes higher heat capacity because more energy is required to increase the temperature of the system when the system is more packed (denser). Could think about the density of states?

Example input code used to simulate of d=0.2 t=2.0

### DEFINE SIMULATION BOX GEOMETRY ###
variable density equal 0.2

lattice sc ${density}
region box block 0 15 0 15 0 15
create_box 1 box
create_atoms 1 box

### DEFINE PHYSICAL PROPERTIES OF ATOMS ###
mass 1 1.0
pair_style lj/cut/opt 3.0
pair_coeff 1 1 1.0 1.0
neighbor 2.0 bin

### SPECIFY THE REQUIRED THERMODYNAMIC STATE ###
variable T equal 2.0
variable timestep equal 0.0025

### ASSIGN ATOMIC VELOCITIES ###
velocity all create ${T} 12345 dist gaussian rot yes mom yes

### SPECIFY ENSEMBLE ###
timestep ${timestep}
fix nve all nve

### THERMODYNAMIC OUTPUT CONTROL ###
thermo_style custom time etotal temp press
thermo 10

### RECORD TRAJECTORY ###
dump traj all custom 1000 output-1 id x y z

### SPECIFY TIMESTEP ###

### RUN SIMULATION TO MELT CRYSTAL ###
run 10000
unfix nve
reset_timestep 0

### BRING SYSTEM TO REQUIRED STATE ###
variable tdamp equal ${timestep}*100
fix nvt all nvt temp ${T} ${T} ${tdamp}
run 10000
unfix nvt
fix nve all nve
reset_timestep 0

### MEASURE SYSTEM STATE ###
thermo_style custom step etotal temp atoms 
variable x2 equal atoms*atoms
variable energy equal etotal
variable energy2 equal etotal*etotal
variable temp equal temp
variable temp2 equal temp*temp
variable x equal atoms

fix aves all ave/time 100 1000 100000 v_energy v_energy2 v_temp v_temp2 
run 100000

variable CV equal (((f_aves[2]-f_aves[1]*f_aves[1])/(f_aves[4]))*${x2})
variable avt equal f_aves[3]

print "Temperature: ${avt}"
print "Heat Capacity: ${CV}"
print "Atoms: ${Number}

Structural properties and the radial distribution function

TASK: perform simulations of the Lennard-Jones system in the three phases. When each is complete, download the trajectory and calculate g(r) and \int g(r)\mathrm{d}r. Plot the RDFs for the three systems on the same axes, and attach a copy to your report. Discuss qualitatively the differences between the three RDFs, and what this tells you about the structure of the system in each phase. In the solid case, illustrate which lattice sites the first three peaks correspond to. What is the lattice spacing? What is the coordination number for each of the first three peaks?

RDF of solid, liquid and gas

Integral of g(r) for solid, liquid and gas

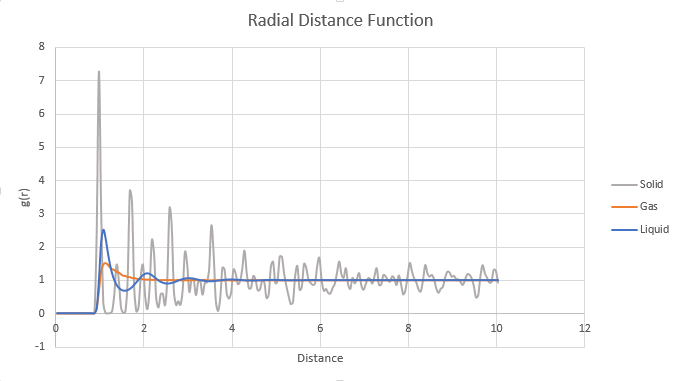
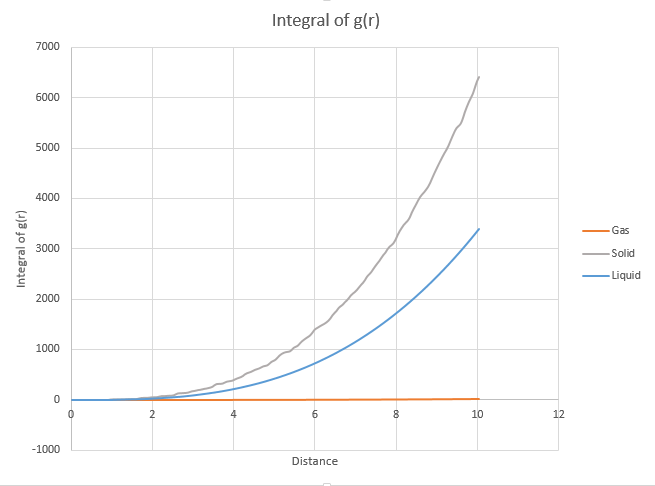
• RDF shows how the effective density of particles related from a reference particle and therefore different phased molecules have different RDF.Tick

• The integral of g (r) is the area under the RDF curves which is the density of the particles Only for a normalised rdf..

• RDF of solid shows that more ordered structure of solid compare to liquid or vapour as solid is more packed and the distance between the particles is shorter than that of liquid and vapour which is shown from the large amplitude of the peaks Think about long-range order... For a solid, this is large!

• Liquid has fewer peaks and lower amplitude compare to solid due to the increase of the number of degrees of freedom. Well, you do get dynamic averaging hence the smoothness but you should qualitatively explain such phenomena in terms of order. Although correct...

• Vapour shows one maxima before it decreases to 1 as the vapour system is highly disordered.Reference particle --> no order

Lattice sites

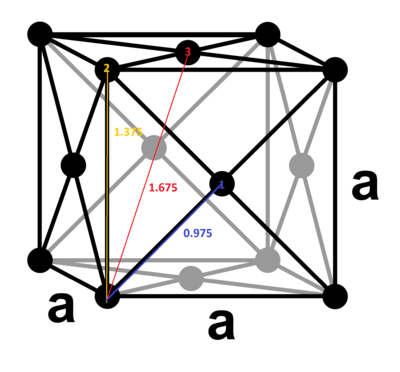
The above image shows the first three nearest neighbour.

The coordination number for the first three peaks

• 1st nearest neighbour:12 (0.975, 7.264)
• 2nd nearest neighbour:6 (1.375, 1.460)
• 3rd nearest neighbour:24 (1.675, 3.670)

Lattice spacing: 1.375 Tick

Dynamic properties and the diffusion coefficient

Mean Squared Displacement

TASK: In the D subfolder, there is a file liq.in that will run a simulation at specified density and temperature to calculate the mean squared displacement and velocity autocorrelation function of your system. Run one of these simulations for a vapour, liquid, and solid. You have also been given some simulated data from much larger systems (approximately one million atoms). You will need these files later.

TASK: make a plot for each of your simulations (solid, liquid, and gas), showing the mean squared displacement (the "total" MSD) as a function of timestep. Are these as you would expect? Estimate D in each case. Be careful with the units! Repeat this procedure for the MSD data that you were given from the one million atom simulations.

Total Mean Squared Displacement against timesteps

Total Mean Squared Displacement against timesteps of million atoms

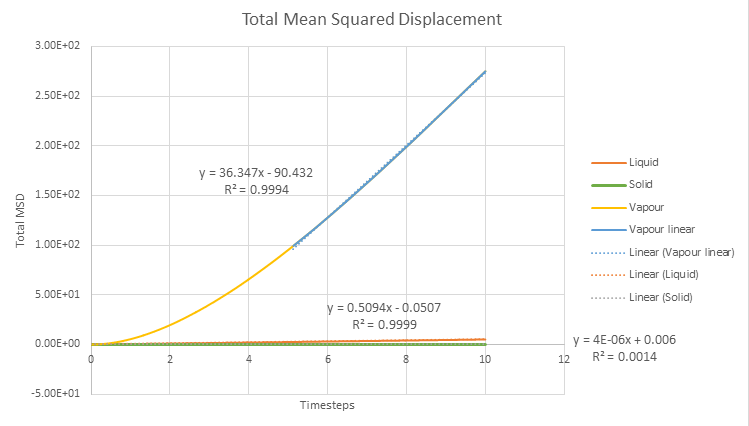
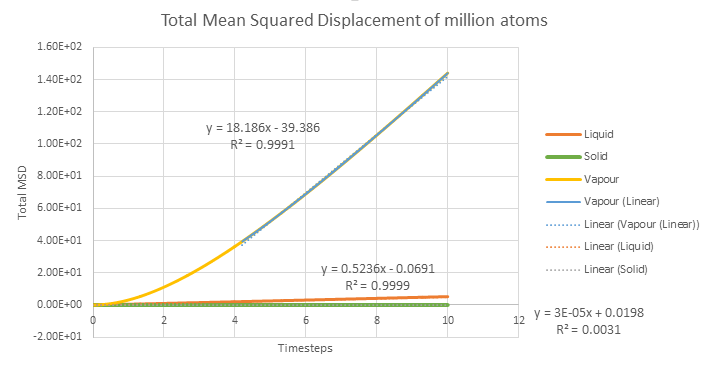
Diffusive coefficients were calculated using mean squared displacement graph $D=\frac{1}{6}\frac{\partial ⟨r^2\left(t\right)⟩}{\partial t}$

and Velocity Autocorrelation Function graph. $D=\frac{1}{3}\underset{0}{\overset{\mathrm{\infty }}{\int }}\mathrm{d}\tau ⟨\mathbf{v}\left(0\right)\cdot \mathbf{v}\left(\tau \right)⟩$ These calculated values are shown below.

D values from MSD	D values from MSD of million atoms	D values from VACF	D values from VACF of million atoms
D (Vapour): 6.06	D (Vapour): 3.03	D (Vapour): 6.34	D (Vapour): 3.27
D (Liquid): 0.0849	D (Liquid): 0.0873	D (Liquid): 0.098	D (Liquid): 0.090
D (Solid): 6.7E-7	D (Solid): 5E-7	D (Solid): 1.13E-5	D (Solid): 4.6E-5

The trend of the MSD against timestep for the simulation and or one million atoms are expected trend. The vapour has much higher MSD compare to liquid and solid as it has higher degree of freedom and disordered system and therefore vapour has the highest diffusion coefficient. The solid has the lowest diffusion coefficient and MSD as the solid system is highly ordered system and therefore the particles are harder to displace. Except the D value for the vapour, D values for solid and liquid of the simulation are very similar with the D values of million atoms suggesting the increasing the number of atoms does not change diffusion coefficient of the system. Tick but the millions atom simulation should be more accurate...

Velocity Autocorrelation Function

TASK: In the theoretical section at the beginning, the equation for the evolution of the position of a 1D harmonic oscillator as a function of time was given. Using this, evaluate the normalised velocity autocorrelation function for a 1D harmonic oscillator (it is analytic!):

$C\left(\tau \right)=\frac{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}v\left(t\right)v(t+\tau )\mathrm{d}t}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{v}^2\left(t\right)\mathrm{d}t}$

Displacement of the system is

$x\left(t\right)=A\cos (\omega t+\varphi )$

To get velocity, displacement needs to be differentiated with time
$\frac{\partial \left(x\left(t\right)\right)}{\partial t}=v\left(t\right)$

Velocity of the system is
$v\left(t\right)=-\omega A\sin (\omega t+\varphi )$

$C\left(\tau \right)=\frac{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}-A\omega \sin (\omega t+\varphi )v(t+\tau )\mathrm{d}t}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{A}^2{\omega }^2{\sin }^2(\omega t+\varphi )\mathrm{d}t}$

$C\left(\tau \right)=\frac{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}-A\omega \sin (\omega t+\varphi )\times -A\omega \sin (\omega (t+\tau )+\varphi )\mathrm{d}t}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{A}^2{\omega }^2{\sin }^2(\omega t+\varphi )\mathrm{d}t}$

$C\left(\tau \right)=\frac{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}A\omega \sin (\omega t+\varphi )\times A\omega \sin (\omega t+\omega \tau +\varphi )\mathrm{d}t}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{A}^2{\omega }^2{\sin }^2(\omega t+\varphi )\mathrm{d}t}$

From the trigonometric identity $\sin (\alpha +\beta )=\sin \left(\alpha \right)\cos \left(\beta \right)+\sin \left(\alpha \right)\cos \left(\beta \right)$

Let $(\omega t+\varphi )=\alpha$ and $\omega \tau =\beta$

$\sin (t+\tau )=\sin (\omega t+\varphi )\cos \left(\omega \tau \right)+\sin \left(\omega \tau \right)\cos (\omega t+\varphi )$

$C\left(\tau \right)=\frac{A^2{\omega }^2\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\sin (\omega t+\varphi )\times \sin (\omega (t+\tau )+\varphi )\mathrm{d}t}{A^2{\omega }^2\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{\sin }^2(\omega t+\varphi )\mathrm{d}t}$

$C\left(\tau \right)=\frac{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\sin (\omega t+\varphi )\times [\sin (\omega t+\varphi )\cos \left(\omega \tau \right)+\sin \left(\omega \tau \right)\cos (\omega t+\varphi )]\mathrm{d}t}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{\sin }^2(\omega t+\varphi )\mathrm{d}t}$

$C\left(\tau \right)=\frac{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\sin (\omega t+\varphi )\times \sin (\omega t+\varphi )\cos \left(\omega \tau \right)\mathrm{d}t+\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\sin (\omega t+\varphi )\sin \left(\omega \tau \right)\cos (\omega t+\varphi )\mathrm{d}t}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{\sin }^2(\omega t+\varphi )\mathrm{d}t}$

As $\cos \left(\omega \tau \right)$ and $\sin \left(\omega \tau \right)$ can be assumed as constant, they can be taken our from the integral

$C\left(\tau \right)=\frac{\cos \left(\omega \tau \right)\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{\sin }^{}(\omega t+\varphi )\mathrm{d}t+\sin \left(\omega \tau \right)\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\sin (\omega t+\varphi )\cos (\omega t+\varphi )\mathrm{d}t}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{\sin }^2(\omega t+\varphi )\mathrm{d}t}$

$C\left(\tau \right)=\cos \left(\omega \tau \right)+\frac{\sin \left(\omega \tau \right)\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\sin (\omega t+\varphi )\cos (\omega t+\varphi )\mathrm{d}t}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{\sin }^2(\omega t+\varphi )\mathrm{d}t}$

As the second term of above equation contains odd function making whole second term to 0.
$\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\sin (\omega t+\varphi )\cos (\omega t+\varphi )\mathrm{d}t=0$

$\frac{\sin \left(\omega \tau \right)\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\sin (\omega t+\varphi )\cos (\omega t+\varphi )\mathrm{d}t}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{\sin }^2(\omega t+\varphi )\mathrm{d}t}\to 0$

$\therefore C\left(\tau \right)=\cos \left(\omega \tau \right)$ Tick

Be sure to show your working in your writeup. On the same graph, with x range 0 to 500, plot $C\left(\tau \right)$ with $\omega =1/2\pi$ and the VACFs from your liquid and solid simulations. What do the minima in the VACFs for the liquid and solid system represent? Discuss the origin of the differences between the liquid and solid VACFs. The harmonic oscillator VACF is very different to the Lennard Jones solid and liquid. Why is this? Attach a copy of your plot to your writeup.

Velocity Autocorrelation Function against time

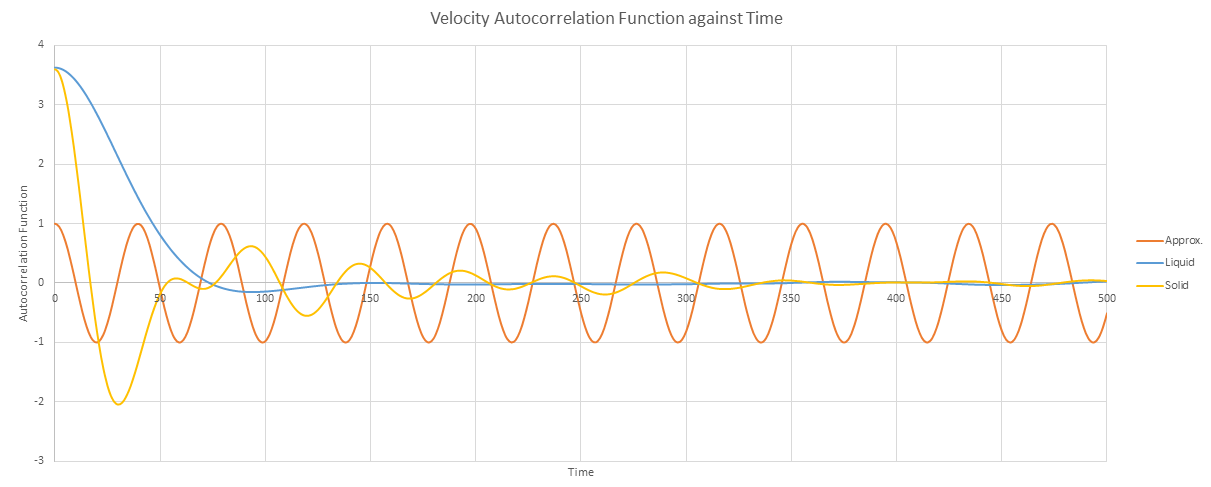
For liquids and solids atoms are favourable to be at the most stable energy state.? For solids because atoms cannot move away easily from their positions, the atoms vibrate, reversing their velocity at the end of each oscillation. ? This is shown from the graph which the solid VACF graph oscillate strongly compare to liquids. The magnitudes of this graph are not the same because they will decay in time as the perfection of their oscillatory motion is disrupted from perturbation and collision as they oscillates resulting in damped oscillation. The minima of the liquid and solid system represent the reversing of velocity.Not correct, the minimum is the point at which all of the atoms have collided once. Think about things in terms of fundamental correlation Because liquids are not fixed at regular positions oscillatory motion decays rapidly because of the presence of diffusive motion. Because there is no disruption from perturbation, collision and diffusive motion the harmonic oscillator VACF shows the perfect oscillation as shown from the graph.

TASK: Use the trapezium rule to approximate the integral under the velocity autocorrelation function for the solid, liquid, and gas, and use these values to estimate D in each case. You should make a plot of the running integral in each case. Are they as you expect? Repeat this procedure for the VACF data that you were given from the one million atom simulations. What do you think is the largest source of error in your estimates of D from the VACF?

Integral value against Time

Integral value against Time of million atoms

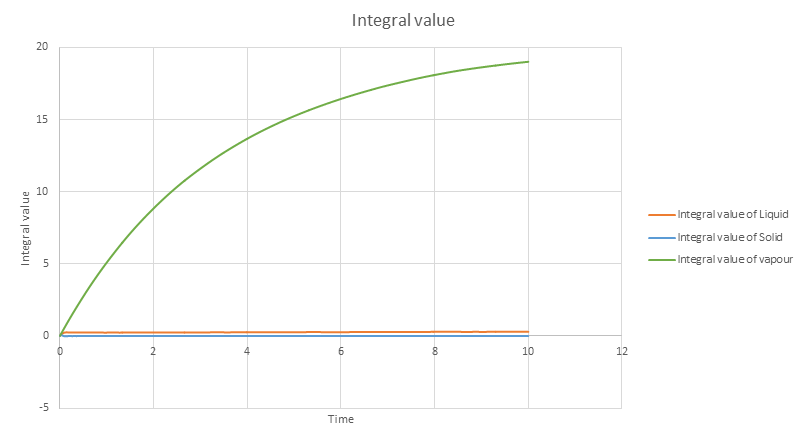
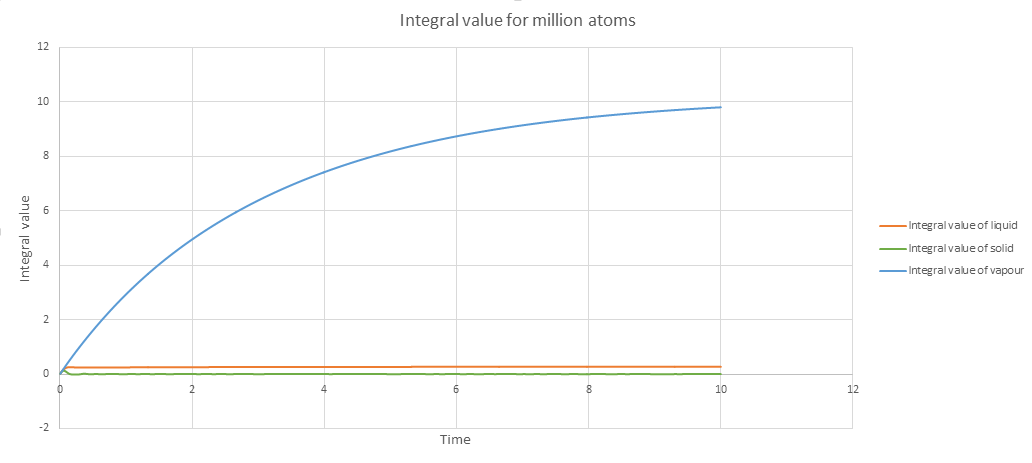
The trend of the integral values graph is expected trend. The vapour has the largest area under the curve, and then liquid and then solid. Because VACF graph of solid shows strong oscillation, the total area under the curve is the smallest. And because the vapour VACF graph does not show any oscillation as the position of the particles are not fixed and the vapour system is disordered, vapour has the highest area under the curve as shown from the above graph. The values obtained using trapezium rule to estimate diffusive coefficients from VACF are relatively bigger than the diffusive coefficients from mean squared displacement because of the overestimation.Tick