Rep:Mod:PCompTO
Physical Computational Lab
The Cope Rearrangement
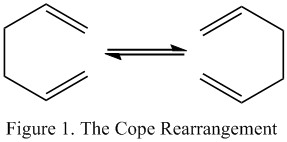
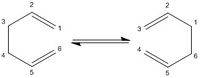
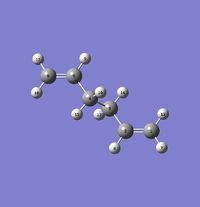
The Cope Rearrangement of 1,5-hexadiene is a [3,3] sigmatropic shift which can be seen on the right hand side in Figure 1. The Objective of this first part of the lab is to locate the low energy minima and transition states structures on the 1,5-hexadiene potential energy surface and hence determine the favoured mechanism.
Optimizing the Reactants and Products
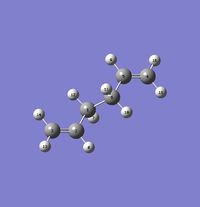
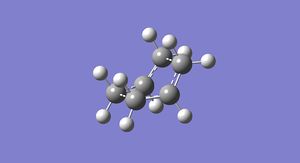
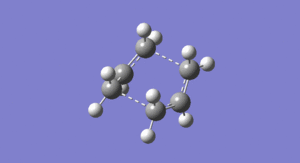
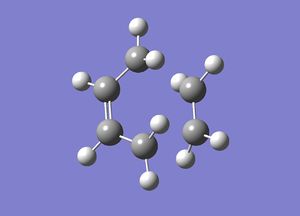
In this first section, conformers of 1,5-hexadiene were optimized to their lowest energy. Firstly a molecule of 1,5-hexadiene with an antiperiplanar linkage across the four central C atoms was drawn and optimized at the HF/3-21G level. This was followed by optimizing a gauche conformer at the same level of theory. The two conformers can be seen below in Figure 2.
|
| ||||||
| Anti Conformer | Gauche Conformer |
By comparing the energies of the optimized conformers with those in Appendix 1 , it could be seen that the anti conformer was the same as the 'anti 1' structure and the gauche conformer was the same as the 'gauche 2' conformer. The results of the optimizations can be seen below in Table 1 and Table 2.
|
|
It can be seen that the the anti conformer here is lower in energy than the gauche conformer. This most likely due a steric repulsion that occurs in the gauche conformer between the two terminal alkene groups that does not occur in the anti conformer.
The 'anti 2' conformer of 1,5-hexadiene (Figure 3) was optimized using the HF/3-21G level of theory. It was then reoptimized using the B3LYP/6-31G* level of theory. The results are shown below in Table 3 and Table 4.
|
|
|
Comparing the structures between the two different optimization theories used, it can be seen that the central C-C bond shortened from HF/3-21G (1.55282 Å) to the B3LYP/6-31G* (1.54808 Å). The C-C bond between one of the central carbons and an alkene carbon also shortens from 1.50888 Å to 1.50421 Å. However the alkene bonds elongate from 1.31614 Å to 1.33352 Å.
Although the structures do change slightly with reoptimization, the most importance difference is the change in energy of the minimum structure which decreases from -231.6925353 a.u to -234.6117104 a.u.
A frequency calculation was then carried out on the 'anti 2' conformer using the B3LYP/6-31G* level of theory. The purpose of this was to confirm that the structure that was found was a minima on the potential energy surface. If the vibrations are all real and positive, the structure is at the minima. After the calculation it was found that their were no imaginary vibrational modes and hence it can be said that the structure is at a minima. The simulated vibrational spectrum can be seen in Figure 4.
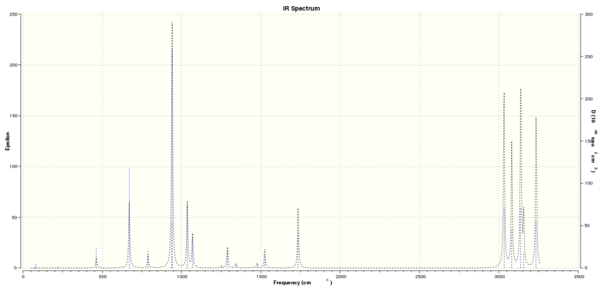
The frequency calculation also provides thermodynamic data about the 'anti 2' conformer. These are presented in Table 5.
| Sum of electronic and zero-point Energies = | -234.469204 | a.u |
| Sum of electronic and thermal Energies = | -234.461857 | a.u |
| Sum of electronic and thermal Enthalpies = | -234.460913 | a.u |
| Sum of electronic and thermal Free Energies = | -234.500777 | a.u |
Optimizing the Chair and Boat Transition Structures
The Cope rearrangement of 1,5-hexadiene can proceed via either a chair or boat transition state as seen in Figure 5. The objective of this section is to optimize the transition structures using three different methods. Then the activation energies for the Cope rearrangement via the two different transition structures were found.
The Chair Transition Structure
Firstly an allyl (CH2CHCH2)fragment was optimized using the HF/3-21G level of theory. This can be seen in Figure 6.
Allyl Frag |
Two allyl fragement were then placed with on top of the other in a rough chair configuration with the terminal carbons 2.2 Å apart. This provided a guess for the transition state optimizations that were performed next. This guess structure can be seen in Figure 7.
First Transition Structure Optimization
The first way in which a transition structure optimization was done, was using the Hessian Method. This was done by running an Opt+Freq calculation to a transition state (instead of a minimum) using the Berny Algorithm with the force constants calculated once. This was done to the HF/3-21G level of theory and the additional keyword Opt=NoEigen was added. This keyword prevents the calculation from crashing if more than one imaginary frequency is present. This calculation gave the transition structure seen inFigure 8. The structure had changed from the guessed transition structure in that the the terminal carbons of the allyl fragments were now 2.2050 Å apart. The transition structure also had an imaginary frequency at -817.97 cm-1 which corresponds to the Cope rearrangement as seen in Figure 9.
The transition structure had an energy of -231.619322 a.u and a point group of C2h. This agrees well with the structure found in appendix 2.
Second Transition Structure Optimization
The second way the chair transition structure was optimized was using a frozen co-ordinate method. Firstly all four terminal carbons on the allyl fragments were frozen using the Redundant Coordinate Editor by selecting the required bonds and choosing Freeze Coordinate. The structure was then optimized to a minimum using the HF/3-21G level of theory. On completion it could be seen that the terminal carbons remained the same distance apart as they were in the guess transition structure (~2.2 Å). The bond forming/breaking atoms were then optimized using the Redundant Coordinate Editor, selecting the required bonds and choosing Derivative. An optimization to a transition state using the Berny algorithm was then carried out, however this time the force constants were not calculated. This calculation gave the transition structure seen in Figure 10. The C-C distance between the bond forming/breaking carbons have changed from 2.2 Å (in the guess structure)to 2.20205 Å and 2.2070 Å (in the optimized transition structure). This method also yielded an imaginary frequency in the transition structure at -817.83 cm-1 which corresponds to the bond breaking and forming action of the Cope rearrangement. This can be seen in Figure 11.
The transition structure had an energy of -231.619322 a.u and a point group of C2h. This agrees well with both the structure found in appendix 2 and the one found using the Hessian method above.
The Boat Transition Structure
The boat transition structure was optimized using the QST2 method where the reactants and products were specified and the transition structure was interpolated from these. Firstly the optimized Ci 'anti 2' 1,5-hexadiene molecule was added as both the product and reactant by labeling the atoms to show this as seen in Figure 12 and 13.
The transition structure was then found by running an Opt+Freq calculation to a transition state (QST2) using the HF/3-21G level of theory. However it was found that this calculation failed and the output slightly resembled the chair transition structure as can be seen in Figure 14.
This is because the calculation did not consider the the option of rotating around the central bonds and hence the reactant and product molecules needed o be modified to more closely resemble the boat transition structure. The modified reactants and products can be seen in Figure 15.
The QST2 calculation was run again (using the same parameters as before) and this yielded the boat transition structure seen in Figure 16. The distance between the bond forming and bond breaking carbons in this transition structure are 2.1396 Å and 2.1397 Å. The transition structure has an imaginary frequency at -839.93 cm-1. This corresponds to the cope rearrangement and can be seen in Figure 17.
The transition structure had an energy of -231.602802 a.u and a point group of C2v. This agrees well with the structure found in appendix 2.
IRC Calculations
It is almost impossible to identify the conformer that will form from each transition state and therefore an intrinsic reaction coordinate (IRC) method is used to determine this. Using the optimized transition structures from the previous part of the experiment an IRC calculation was completed. It was only done in the forward direction as the reaction coordinate is symmetrical and the force constants were calculated at every step along the IRC. The number of points along the the IRC was set to 50 and for both transiton structures this led to a convergence to the minimum structures so no additional calculations were needed.
Chair Transition Structure IRC
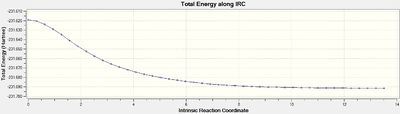
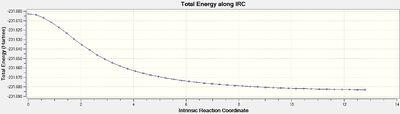
The chair transition structure obtained via the Hessian method (above) was used for the IRC calculation. The formation of the minimum structure from the transition structure can be seen in Figure 18 alongside the reaction co-ordinate in Figure 19.
The intrinsic reaction coordinate calculation converged after only 44 steps out of the set 50 meaning no further calculations were necessary. The minimum structure obtained has an energy of -231.691579 a.u and the point group C2. This corresponds to the 'gauche 2' conformer that was optimized in the previous part of the experiment. It also agrees well with the values in appendix 2 of the lab script.
Boat Transition Structure IRC
The boat transition structure obtained via the QST2 method was used for the IRC calculation. The formation of the minimum structure can be seen in Figure 20 and the reaction co-ordinate can be seen in Figure 21.
The intrinsic reaction co-ordinate calculation converged after 45 steps out of the set 50, so no additional calculations were necessary. The minimum structure obtained has an energy of -231.682982 a.u and the point group Cs. This does not correspond to any of the low energy conformer of 1,5-hexadiene, suggesting that the reaction may not proceed via the boat transition structure.
Activation Energies
To calculate the activation energies of the reaction, the transition structures were reoptimized using the B3LYP/6-31G level of theory and then subjected to a frequency calculation. By comparing the energies of the transition structure to the minimum structures, the activation energies could be found.
Chair TS B3LYP/6-31G* Optimized
The reoptimized structure can be seen below in Figure 22.
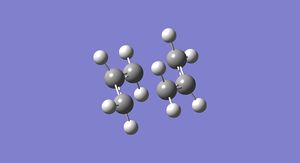
It has an energy of -234.556983 a.u and the point group C2h. It also has a bond distance of 1.96755 Å between the terminal carbon atoms of the allyl fragments. This is shortened when compared to HF/3-21G optimized chair transition structure.
| Sum of electronic and zero-point Energies = | -234.414929 | a.u |
| Sum of electronic and thermal Energies = | -234.409009 | a.u |
| Sum of electronic and thermal Enthalpies = | -234.408065 | a.u |
| Sum of electronic and thermal Free Energies = | -234.443814 | a.u |
Boat TS B3LYP/6-31G* Optimized
The reoptimized structure can be seen in Figure 23.
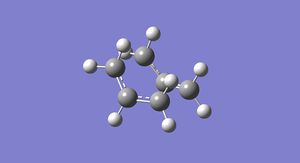
It has an energy of -234.543093 a.u and the point group is C2v. It also has bond distances of 2.20871 Å and 2.20793 Å between the terminal carbons of the allyl fragments. These are longer than those in the HF/3-21G level of theory.
| Sum of electronic and zero-point Energies = | -234.402350 | a.u |
| Sum of electronic and thermal Energies = | -234.396014 | a.u |
| Sum of electronic and thermal Enthalpies = | -234.395070 | a.u |
| Sum of electronic and thermal Free Energies = | -234.431762 | a.u |
By comparing these energies with those of the reactant (the 'anti 2' 1,5-hexadiene conformer), the activation energies for each transition structure were found.
| HF/3-21G | B3LYP/6-31G* | |||||
|---|---|---|---|---|---|---|
| Electronic energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | Electronic energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | |
| at 0 K | at 298.15 K | at 0 K | at 298.15 K | |||
| Chair TS | -231.619322 | -231.466700 | -231.461341 | -234.556983 | -234.414929 | -234.409009 |
| Boat TS | -231.602802 | -231.450922 | -231.445294 | -234.543093 | -234.402350 | -234.396014 |
| Reactant (anti2) | -231.692535 | -231.539540 | -231.532566 | -234.611710 | -234.469204 | -234.461857 |
All energies above in a.u
Summary of activation energies (in kcal/mol)
| HF/3-21G | HF/3-21G | B3LYP/6-31G* | B3LYP/6-31G* | Expt. | |
| at 0 K | at 298.15 K | at 0 K | at 298.15 K | at 0 K | |
| ΔE (Chair) | 45.71 | 55.61 | 34.06 | 33.16 | 33.5 ± 0.5 |
| ΔE (Boat) | 44.69 | 54.76 | 41.95 | 41.32 | 44.7 ± 2.0 |
It can be seen that the activation energies for both the chair and boat transition structures agree with the experimental values. This means the transition structure models were accurate. It can also be seen that the chair transition structure has a lower activation energy than the transition structure meaning this pathway is favoured and the reaction will proceed via the chair transition state. This agrees with the IRC calculation above in which the boat transition structure did not lead to a minimum structure.
Diels Alder Cycloaddition
The Diels Alder reaction is a [4+2] cycloaddition between a diene and a dieneophile (REF) as seen in Figure 24 (FIG). The reaction occurs due to an overlap in symmetry between the reactant and product HOMOs and LUMOs. If the HOMO of one reactant can overlap with the LUMO of the other reactant and they both have the same symmetry, then the reaction is allowed. Conversely if the HOMO and lUMO are of opposite symmetry then the reaction is forbidden.
The HOMO and LUMO of Cis Butadiene and Ethylene
The structures of both cis-butadiene and ethylene were optimized using the Semi Empirical AM1 level of theory. This enabled the HOMO and LUMO of each reactant to be viewed.
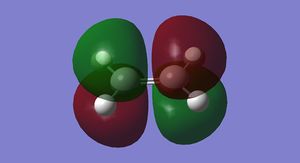
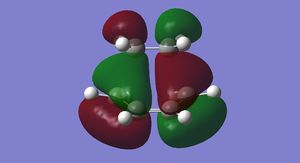
The HOMO and LUMO for cis-butadiene and ethylene were plotted and are shown below in Figures 25-28.
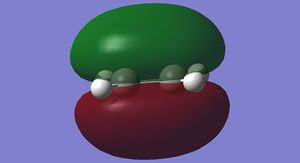
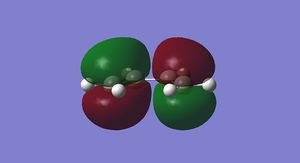
It can be seen that the ethylene LUMO and the cis-butadiene HOMO are both anti symmetric. Conversely the ethylene HOMO and the cis-butadiene LUMO are both symmetric. This means that the reaction is allowed.
Cyclohexene Transition Structure
The transition structure of the reaction between cis-butadiene and ethylene was optimized using a Hessian method as done in the previous part of the experiment. The optimization was done using the Semi Empirical/AM1 level of theory. This gave the transition structure as seen in Figure 29. This has an energy of 0.111655 a.u and a point group of Cs. The distance between the bond-forming carbons is 2.119 Å and 2.120 Å. It also has an imaginary frequency at -955.82 cm-1 which corresponds to the Diels Alder Cycloaddition. This frequency can be seen in Figure 30 below. It can be seen from this that bond forming is synchronous.
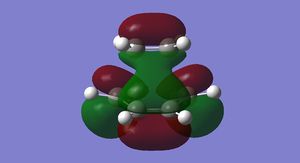
The HOMO and LUMO for this Diels Alder transition structure were also plotted and can be seen below in Figure 31 and 32 below.
It can be seen that the HOMO is antisymmetric and is a mixture of both the ethylene LUMO and the cis-butadiene HOMO. The LUMO on the other hand is symmetric and is a mixture of the ethylene HOMO and the cis-butadiene LUMO. This agrees with orbital analysis above, and further confirms that the reaction is allowed.
As stated before, the distance between the bond forming carbons is about 2.112 Å. An average sp3C-sp3C bond length 1.54 Å while the average sp2C-sp2C bond length is 1.47 Å [1]. The van-der waals radii of a Carbon atom is 1.70 Å and therefore the combined radius is 3.40 Å [2]. Therefore the bond forming carbon atoms clearly feel attractive forces between each other but they are not close enough to be officially termed 'bonded'.
Regioselectivity of the Diels Alder Transition Structure
The reaction between cyclohexadiene and maleic anhydride can lead to two isomers; the endo and exo as seen in Figure 33. The reaction is kinetically controlled so the endo isomer is favoured.
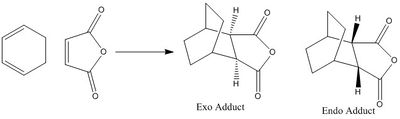
Both the endo and exo transtion states were optimized using the Hessian method that has been used previously. The calculation was run using the Semi Empirical / AM1 level of theory; the transition structures can be seen below.
Endo Transition Structure
The endo transition structure can be seen in Figure 34. It had an energy of -0.051504 a.u , a point group of Cs and carbon bond forming distances of 2.162 Å. The transition structure also has an imaginary frequency at -806.39 cm-1 which corresponds to the Diels Alder exo adduct being formed. This can be seen below in Figure 35.
Exo Transition Structure
The exo transition structure can be seen in Figure 36. It had an energy of -0.050420 a.u , a point group of Cs and carbon bond forming distances of 2.170 Å. The transition structure also has an imaginary frequency at -812.22 cm-1 which corresponds to the Diels Alder exo adduct being formed. This can be seen below in Figure 37.
It can be seen that the endo transition structure is lower in energy than the exo transition structure. This could be due to two reasons. The first is that the C=O Pi system in maleic anhydride interacts favourably with the diene Pi system resulting in a lowering of energy. Also in the exo transition structure there is a steric clash between the maleic anhydride and the -CH2-CH2- bridge resulting in an increase in strain energy that is not felt in the endo transition structure.
Transition Structure HOMOs
The HOMO orbitals for both the endo and exo transition structures were plotted and can be seen below in Figure 38 and Figure 39.
It can be seen from the HOMO of the endo transition structure that there is no interaction between the C=O bond and the diene Pi system as hypothesized above (secondary orbital overlap)[3].
References
- ↑ F. H. Allen, O. Kennard, D. G. Watson, L. Brammer, A. G. Orpen, R. T., J. Chem. Soc., Perkin Trans. 2, 1987, DOI:10.1039/P298700000S1
- ↑ R. S. R. , R. T. , J. Phys. Chem., 1996, 100, 7391 DOI:10.1021/jp953141+
- ↑ Fleming, Ian (1978). Frontier Orbitals and Organic Chemical Reactions. London: Wiley. pp. 29–109. ISBN 0-471-01819-8.