Rep:Mod:PAP0801
Module 1: Modelling using Molecular Mechanics
Introduction:
Molecular mechanics is a useful technique for finding the lowest energy conformation of a molecule, giving optimised values for molecular properties such bond lengths and angles. This allows the difference in the total steric energy of stereoisomers and conformational isomers to be compared. The contributions to the total energy are:
- 1. Stretch: The sum of all the bond vibrations between directly bonded atoms. The equation for this is a parabolic equation based on Hooke's Law.
- 2. Bend: The sum of all equilibrium bond angles that are bonded to the same central atom. The equation for this is also based on Hooke's Law.
- 3: Stretch-Bend: A combination of the stretching and bending vibrations of the molecule.
- 4. Torsion: The rotation of the angle between atoms that are bonded to adjacent atoms. This is based on a periodic function.
- 5. VDW: The sum of all Van der Waals interactions for atoms that are bonded more than two covalent bonds apart. This is an attractive force up to a certain distance, after which the atoms start to repel each other. This is based on the Lennard-Jones potential.
- 6. Dipole-Dipole: The sum of all electrostatic interactions in the molecule. This is based on the Coulomb potential.
The Molecular Mechanics method will be applied to four different examples of isomers in order to find the lowest energy isomer and therefore help predict which product is most likely to be formed in a reaction. The energies are given in kcal mol-1 and are converted to kJ mol-1 for easy comparison with literature data. The individual components of the total energy are meaningless however the difference in the total energy of two isomers can be analysed. ChemBio3D and Gaussian will be used to do this for the following:
- 1. Dimerisation of cylopentadiene and subsequent hydrogenation
- 2. Conformational analysis of a ketone intermediate in the synthesis of Taxol
- 3. Regioselective addition of dichlorocarbene
- 4. The effect of neighbouring group participation on the glycosidation of monosaccharides.
1. The Dimerisation and Hydrogenation of Cyclopentadiene
Dimerisation of Cyclopentadiene
Introduction:
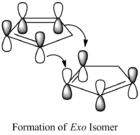
At temperatures above -80oC, cyclopentadiene can dimerise to produce norborenes. It forms an endo isomer and an exo isomer via a Diels-Alder 4πs+2πs cycloaddition reaction[1]. Dicyclopentadiene and its derivatives are important intermediates in the formation of petrochemical products and in the pharmaceutical industry.[2] Kinetically the endo isomer is preferred, as this allows for stabilizing orbital interactions, and this isomer is almost exclusively formed. However, the exo isomer is thermodynamically favoured as seen by the calculations below.
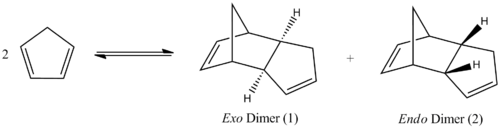
The minimisation of the energy of both isomers was run on ChemBio3D and the results of the calculation can be seen in the table below.
| Stretch(kJ/mol) | Bend(kJ/mol) | Stretch-Bend(kJ/mol) | Torsion(kJ/mol) | Non-1,4 VDW(kJ/mol) | 1,4 VDW(kJ/mol) | Dipole-Dipole(kJ/mol) | Total Energy(kJ/mol) | |
|---|---|---|---|---|---|---|---|---|
| Exo Isomer (1) | 5.38 | 86.10 | -3.51 | 32.03 | -5.93 | 17.72 | 1.58 | 133.37 |
| Endo Isomer (2) | 5.23 | 87.24 | -3.50 | 39.79 | -6.46 | 18.07 | 1.87 | 142.25 |
| Difference in Energy | 0.15 | 1.14 | 0.01 | 7.76 | 0.53 | 0.35 | 0.29 | 8.88 |
  |
As can be seen from the table, the exo isomer is the most stable as it has 8.873kJmol-1 less steric energy than the endo isomer. The largest difference in energy between the two isomers is the torsional energy. This is due to torsional strain in the endo product between C(5) and C(3) of the 5-membered ring and C(9) and C(8) of the 6-membered ring respectively. Therefore the exo isomer is the thermodynamically more favourable product and would appear to be the isomer formed in this reaction.
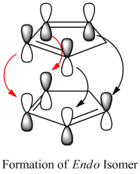
However, according to literature[3], the endo product is the most likely to be formed as this is the kinetically more stable product so it has a lower activation barrier than that for the exo isomer. As the reaction is irreversible under standard conditions, the kinetically more stable product will be the major product. This is due to the orbital interactions between the alkene π orbitals of the cyclopentadiene rings as the rings approach each other in different orientations. In the formation of the exo isomer, the cyclopentadiene rings are orientated so that one double bond from one ring overlaps one double bond from the other. This only allows for primary orbital interactions between the HOMO and LUMO of the alkenes. On the other hand, the cyclopentadiene rings approach each other with each of the double bonds in one ring overlapping the double bonds in the second ring. Therefore, there are primary and secondary interactions in the formation of the endo product which helps stabilise the resulting dimer.
 |
 |
Hydrogenation of Dicyclopentadiene Dimers
The endo cyclopentadiene dimer can be partially hydrogenated using H2 and a palladium/carbon catalyst to form an exo product and an endo product. These can be hydrogenated further to produce the fully hydrogenated tetrahydro derivative. The derivative does not have a specific stereochemistry because bond rotation is no longer restricted by the presence of C=C double bonds.
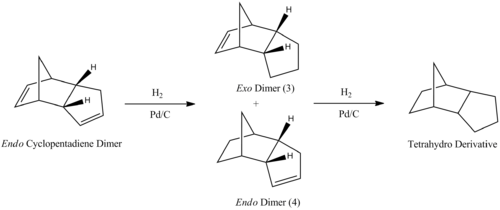
The hydrogenation process occurs with one double bond being hydrogenated at a time. By running MM2 force field calculations using ChemBio3D and comparing the resulting energies, it is possible to determine which double bond in the dicyclopentadiene dimer is hydrogenated first.
| Stretch(kJ/mol) | Bend(kJ/mol) | Stretch-Bend(kJ/mol) | Torsion(kJ/mol) | Non-1,4 VDW(kJ/mol) | 1,4 VDW(kJ/mol) | Dipole-Dipole(kJ/mol) | Total Energy(kJ/mol) | |
|---|---|---|---|---|---|---|---|---|
| Exo Isomer (3) | 5.23 | 80.15 | -3.49 | 46.34 | -6.87 | 24.25 | 0.68 | 146.29 |
| Endo Isomer (4) | 4.56 | 60.87 | -2.28 | 52.31 | -4.52 | 18.85 | 0.59 | 130.38 |
| Difference in Energy | 0.67 | 19.28 | 1.22 | 5.97 | 2.34 | 5.41 | 0.09 | 15.91 |
  |
As can be seen from the table, dimer (4) is more thermodynamically stable than dimer (3) by an energy of 15.913kJmol-1. The greatest difference in energy is from the bending vibrations in the molecule which suggests that one isomer is more strained than the other. In product 3, the double bond in the 6-membered ring is more strained than the double bond in the 5-membered ring due to the alkyl bridge. This distorts the bond angle of the C=C-C bond to 108o which is far less than 120o, as is ideal for a sp2 hybridised carbon. The same bond angle in product 4 is distorted to a much lesser extent (113o) than in 3 so it is thermodynamically more favourable to hydrogenate isomer 4 than it is to hydrogenate isomer 3.
 |
 |
The dimerisation of cyclopentadiene rings is dependent on the kinetics of the reaction as the most electronically stable form of the dicyclopentadiene ring is formed. The MM2 force field calculations for the hydrogenation of this endo isomer show that this reaction is dependent on the thermodynamic stability of the resulting dihydrogen isomers. Therefore the endo dihydrogen isomer is more favoured than the exo isomer.
References and Citations
- ↑ E.Jamroz, Slawomir Galka, Jan Cz Dobrowlski, J. Molecular Structure (Theochem), 2003, 634, 225-233: DOI:10.1016/S0166-1280(03)00348-8
- ↑ D. Skala and J. Hanika, Petroleum and Coal, 2003, 45, 105-108
- ↑ J.E.Baldwin, J. Organic Chem, 1966, 31, 2441-2444 DOI:10.1021/jo01346a003
2. Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol
Molecules 9 and 10 are important atropisomeric intermediates in the synthesis of Taxol, an anti-cancer drug, and are synthesised with the carbonyl group either up (9) or down (10). The isomers interconvert with each other when left standing so the isomer with the lowest energy will be the preferred form. Both MM2 force-field and MMFF92 field will be used to determine which of the isomers is the most stable.

 |
 |
 |
 |
| Conformer | Stretch(kJ/mol) | Bend(kJ/mol) | Stretch-Bend(kJ/mol) | Torsion(kJ/mol) | Non-1,4 VDW(kJ/mol) | 1,4 VDW(kJ/mol) | Dipole-Dipole(kJ/mol) | MM2 Total Energy(kJ/mol) | MMFF94 Total Energy(kJ/mol) |
|---|---|---|---|---|---|---|---|---|---|
| Chair | 13.04 | 56.41 | 1.71 | 97.85 | -10.74 | 64.04 | -9.96 | 212.34 | 305.97 |
| Twist Boat | 13.46 | 58.83 | 12.39 | 113.85 | -9.90 | 71.32 | -9.94 | 239.58 | 334.83 |
| Conformer | Stretch(kJ/mol) | Bend(kJ/mol) | Stretch-Bend(kJ/mol) | Torsion(kJ/mol) | Non-1,4 VDW(kJ/mol) | 1,4 VDW(kJ/mol) | Dipole-Dipole(kJ/mol) | MM2 Total Energy(kJ/mol) | MMFF94 Total Energy(kJ/mol) |
|---|---|---|---|---|---|---|---|---|---|
| Chair | 10.97 | 47.44 | 1.44 | 82.29 | -9.03 | 53.86 | -8.38 | 178.59 | 257.40 |
| Twist Boat | 11.34 | 49.13 | 1.35 | 91.49 | -8.77 | 58.24 | -8.50 | 194.28 | 272.26 |
The results show that in both cases the chair conformation is more stable than the twist boat conformation. Therefore the chair conformers will be used for comparison of the MM2 force field and MMFF94 field calculations. The MM2 and MMFF94 results can not be compared directly as they use different methods of calculation to obtain the minimum energy and the results between the two methods differ in as much as 94 kJmol-1. The main contributions to the overall energy in both intermediates are from the bending vibrations and the torsional strain. This is due to the ring strain of the 9-membered ring which does not allow the optimum bond angle for the sp2 hybridised carbon as it keeps the structure rigid.
| Isomer | Stretch(kJ/mol) | Bend(kJ/mol) | Stretch-Bend(kJ/mol) | Torsion(kJ/mol) | Non-1,4 VDW(kJ/mol) | 1,4 VDW(kJ/mol) | Dipole-Dipole(kJ/mol) | MM2 Total Energy(kJ/mol) | MMFF94 Total Energy(kJ/mol) |
|---|---|---|---|---|---|---|---|---|---|
| Intermediate 9 Chair | 13.04 | 56.41 | 1.71 | 97.85 | -10.74 | 64.04 | -9.96 | 212.34 | 305.97 |
| Intermediate 10 Chair | 10.97 | 47.44 | 1.44 | 82.29 | -9.03 | 53.86 | -8.38 | 178.59 | 257.40 |
| Difference in Energy | 2.07 | 8.97 | 0.27 | 15.56 | 1.71 | 10.18 | 1.58 | 33.75 | 48.57 |
The results show that for both the MM2 force field calculations and the MMFF94 field calculations, intermediate 10, with the carbonyl group pointing down, is lower in energy than intermediate 9, where the carbonyl group is pointing up. Therefore intermediate 10 is the more thermodynamically favoured isomer so the equilibrium for interconversion will lie more to this isomer than the other. The MM2 energies of the parent alkanes of intermediates 9 and 10 are 326.52kjmol-1 and 239.38kJmol-1 respectively. The stability of these products compared to their parent alkenes can be explained by hyperstability of the alkenes[1]. This extra stability is due to the strain exerted on the molecules by the alkene bridgehead. As the bridgehead is over the nine-membered ring, the molecules is of the ideal polycyclic size to be classed as hyperstable.
References and Citations
- ↑ W.F.Maier and P. Schleyer, J. Am. Chem. Soc., 1981, 103, 1891-1900DOI:10.1021/jo00356a016
3. Regioselective Addition of Dichlorocarbene
Compound 12, 9-chloro-1,4,5,8-tetrahydro-4a,8a-methanonapthalene, can undergo electrophilic addition of dichlorocarbene as it is electron deficient. The reason for this reaction can be examined by studying the orbitals of various energy levels using a quantum mechanical approach. The MM2 method is used first to obtain the optimum structure of the molecule followed by MOPAC/PM6 to find the minimum energy and the shapes of all the orbitals in the optimised state. The hydrogenated form of this molecule will also be studied using IR.
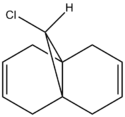 |
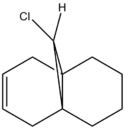 |
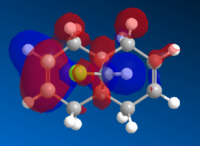
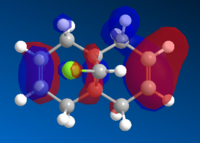
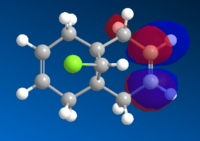
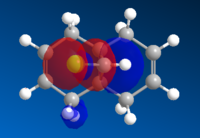
The images below show the relevant molecular orbitals needed to understand the mechanism of the reaction. These should differentiate between the double bonds and thus show which double bond is more nucleophilic.
 |
 |
 |
 |
 |
The molecular orbital images show the HOMO of the molecule is on the alkene which is endo to the Cl-C bond. The shape of the HOMO and HOMO-1 molecular orbitals are as expected because they both show filled pi orbitals over the double bonds. The HOMO-1 shows that the electron density is delocalised over the exo and the endo alkene bonds whereas the HOMO shows no delocalisation. The LUMO shows that the greatest electron density is over the exo double bond. Both this and the molecular orbital arrangement of the HOMO suggest that the endo alkene is the most nucleophilic of the two and therefore would be the site of electrophilic attack by the dichlorocarbene or peracid.
The HOMO-1 pi-orbital over the exo alkene is stabilised lower than the HOMO pi-orbital due to the antiperiplanar overlap caused by the Cl-C σ* bond of the LUMO+2 which further suggests that it is the endo alkene which is involved in electrophilic addition.[1]
The influence of the Cl-C bond on the vibrational frequencies of the molecule can be investigated by comparing compound 12 with the exo-hydrogenated compound 13. This was done by minimising the energy of both molecules using MM2 and MOPAC/PM6 in ChemBio3D and then optimising the geometry in Gaussian. The IR spectra were found by running the Gaussian input file on SCAN using B3LYP/6-31G(d,p). These spectra were analysed to see if there was a differentiation between the exo and endo double bonds in compound 12.
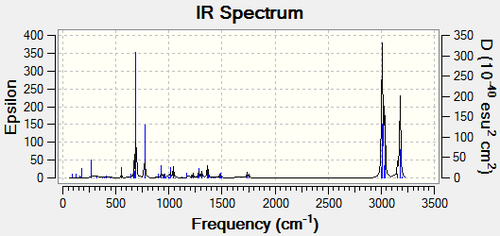 |
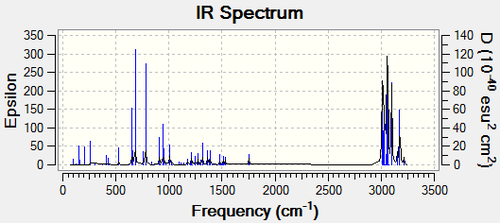 |
The major peaks for both spectra and the alkene and Cl-C stretches are assigned in the table below. Both compounds have a Cs plane of symmetry through the chlorine atom and the rings, dissecting the double bonds.
| C-C Stretch | C=C-H Bend | Cl-C Stretch | C=C Exo Stretch | C=C Endo Stretch | C=C-H Endo Stretch | C=C-H Exo Stretch |
|---|---|---|---|---|---|---|

|
||||||
| 548.77 | 689.57 | 770.80 | 1737.03 | 1757.44 | 3176.09 | 3178.58 |
| C-C Stretch | C=C-H Bend | Cl-C Stretch | C=C Endo Stretch | C=C-H Endo Stretch |
|---|---|---|---|---|

|
||||
| 528.66 | 654.04 | 779.93 | 1753.76 | 3174.92 |
The IR spectra of compound 12 and compound 13 are very similar in that they both have C-C, C=C and alkene-H stretches in the same region. However, the Cl-C stretch occurs at a lower frequency in compound 12 which suggests that the Cl-C bond in compound 12 is weaker than in compound 13. This may be due to the pi-electrons in the exo bond being donated into the Cl-C σ* bond. The IR spectrum for molecule 12 shows two small C=C stretches, which are produced by the two different alkenes, and two different alkene-H stretches also from the different alkenes. On the other hand, the IR spectrum for molecule 13 only shows one C=C stretch and one alkene-H stretch from the endo alkene so although the IR spectra are similar, they can be used to distinguish between the two molecules. As the relevant peaks are very small, determination of the peaks is best done using computational methods.
References and Citations:
- ↑ B. Halton, R. Boese and H.S. Rzepa, J. Chem. Soc. Perkin Trans. 2, 1992, 447-448DOI:10.1039/P29920000447
4. Monosaccharide Chemistry: Glycosidation
Sugar molecules can undergo glycosidation reactions when attacked by a nucleophile which replaces the X leaving group. The α- and β-anomers of the monosaccharides below can be formed due to neighbouring group participation from the adjacent acetyl group.
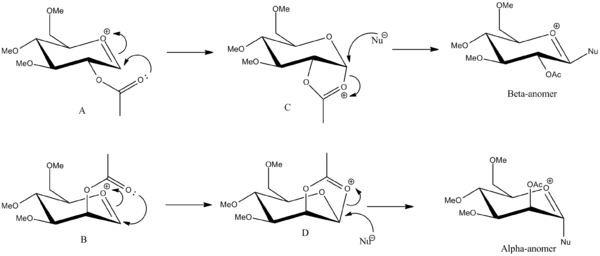
The β-anomer is formed from the attack of a nucleophile (Nu) from the bottom face of the oxonium cation and the α-anomer is formed from the attack of the nucleophile from the top face of the oxonium cation. The anomers A and B can then be rearranged to have the C=O bond of the acetyl group facing away from the C=O+ bond of the cation to form A' and B'. The structures were sketched using ChemBio3D, making sure the hydrogen were in the appropriate equitorial and axial positions for the monosaccharide drawn. Methyl groups were used as the R group as it kept the computational demands to a minimum.
The MM2 force field and MOPAC/PM6 force fields were used to minimise the energy of the molecule after the lowest energy structure had been found by adjusting the positions of the equitorial and axial groups manually.
| Structure | A | A' | B | B' |
|---|---|---|---|---|
| Jmols |
|
|
| |
| Position of Acetyl Group | down | down | up | up |
| MM2 Energy (kJmol-1) | 85.81 | 114.73 | 102.42 | 133.30 |
| MOPAC/PM6 Energy (kJmol-1) | -383.51 | -322.59 | -370.41 | -317.36 |
As structures A and B are not interchangeable, the results of their energy calculations can not be compared. However, A and A', and B and B' can convert between each other so they can be compared. MM2 force field calculations show that the structures of A and B where the acyl C=O group is pointing towards the oxonium ion are more stable than their counterparts where the acyl C=O group is pointing away from the oxonium ion. This is because there is greater orbital overlap of the oxygen of the acyl group and the oxygen of the oxonium ion which stabilises the molecules. The MOPAC energies are given as negative values so the the closer the energies are to zero, the more stable the structure. Therefore the MOPAC calculations support the MM2 calculations as they both show that A is more stable than A' and B is more stable than B'. The trajectory of attack of the nucleophile is also better for structures A and B than for A' and B' which adds to their stability.
The same calculations using MM2 and MOPAC can also be applied to C, C', D and D'. In molecules C and D, the hydrogen atoms on the carbons at the joining of the 5-membered and 6-membered rings are cis to each other whereas in molecules C' and D', the equivalent hydrogen are trans to each other.
| Structure | C | C' | D | D' |
|---|---|---|---|---|
| Jmols |
|
|
| |
| Position of Acetyl Group | down | down | up | up |
| Orientation of H at bicyclic carbons | cis | trans | cis | trans |
| MM2 Energy (kJmol-1) | 133.80 | 186.10 | 108.62 | 171.00 |
| MOPAC/PM6 Energy (kJmol-1) | -383.46 | -282.34 | -383.42 | -278.24 |

The results of these calculations show that using the MOPAC method, C has the same energy as A whereas when the MM2 method is used, they are shown to have different energy. This is because the MOPAC/PM6 does not take into account neighbouring group effects and can not distinguish between A and C. Therefore the MOPAC energies of B and D should also be the same but the results show they are not. This could be because the geometry of either B or D was not optimised completely before being submitted to MOPAC calculations.
MM2 results show that C' is less stable than C by 52.30kJmol-1 and D' is less stable than D by 62.38kJmol-1. These significant differences in energy are due to the anomeric effect which only occurs when the substituents on the ring are in the correct position; ie when they are axial. This allows for orbital overlap between the oxygen lone pair on the ring and the C-O σ* of the oxonium ion. When the latter orbital is in the axial position, there is good overlap between the orbital, however if the same orbital is in the equitorial position, the overlap is extremely poor.
Mini-Project
The mini-project initially chosen was to differentiate between two of the four isomers of methyl 1-amino-3-(4-bromophenyl)cyclopentanecarboxylate[1] using MM2 force field minimisation and Gaussian to produce the 13C NMR of both molecules. Both isomers are rigid as they contain a 5-membered ring so the NMR could be easily generated.
By assigning the peaks to the carbon atoms in the molecule, the isomers could be distinguished. However, the literature NMR showed that the largest difference in the chemical shifts between the isomers was only 2ppm which is within the error limits of the computational method. Therefore this was not a suitable example of differentiating between isomers using spectroscopic methods. A few more papers were looked at however in all the papers, the 13C NMR spectra of both isomers were too similar to differentiate between so one of the mini-projects proposed was investigated.
Assigning Regioisomers in Click Chemistry
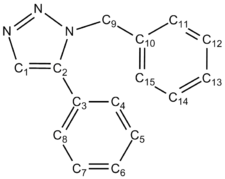
Azides and alkynes can undergo 1,3-dipolar cycloadditions to form 1,2,3-triazoles. The rate of this reaction can be greatly increased by the use of a Cu(I) catalyst and is therefore an example of "click chemistry". This involves the fast and reliable generation of molecules from smaller units and is used throughout nature and in the pharmaceutical industry. The reaction below involves the formation of two isomers; 1-benzyl-4-phenyl-1H-1,2,3-triazole (A) and 1-benzyl-5-phenyl-1H-1,2,3-triazole (B).
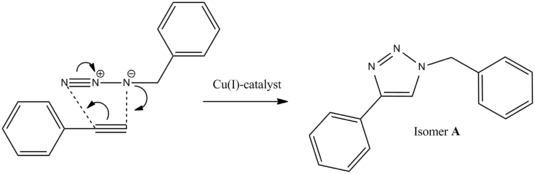 |
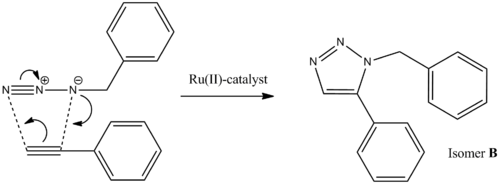 |
The use of Cu(I)-catalyst gives the 1,4-isomer as the major product, however when the Ru(II)-catalyst is used, the 1,5-isomer predominates. These two isomers can be told apart using 13C NMR methods by optimising the geometry of both isomers using MM2 and then submitting it to SCAN for minimisation of the energy. The output file is the re-submitted to SCAN to calculate the 13C NMR in CDCl3; the same solvent used in the literature spectrum.[2]
The phenyl groups of each isomer can be arranged either lying above the plane of the 5-membered ring or below the plane of the 5-membered ring, however both forms had very similar energy when subjected to MM2 calculations.
The isomers were put through MM2 and MOPAC/PM6 calculations and the results are summarised in the table below.
 |
 |
 |
 |
| Isomer | Stretch(kJ/mol) | Bend(kJ/mol) | Stretch-Bend(kJ/mol) | Torsion(kJ/mol) | Non-1,4 VDW(kJ/mol) | 1,4 VDW(kJ/mol) | Dipole-Dipole(kJ/mol) | MM2 Total Energy(kJ/mol) | MMFF94 Total Energy(kJ/mol) |
|---|---|---|---|---|---|---|---|---|---|
| Triazole A | 3.24 | 54.85 | -0.12 | -62.08 | -7.02 | 61.59 | -5.88 | 44.58 | 450.85 |
| Triazole B | 4.63 | 76.55 | 0.45 | -65.78 | 3.04 | 60.14 | -6.96 | 72.06 | 450.17 |
| Difference in Energy | 1.39 | 21.70 | 0.57 | 3.70 | 10.06 | 1.45 | 1.08 | 27.48 | 0.68 |
The MM2 results show that the 1,4-triazole isomer is more stable than the 1,5-triazole isomer by about 27.48kJmol-1 with the greatest difference in energy from the bending vibrations. Isomer B has more bending energy as the phenyl groups must be orientated away from each other due to steric repulsions but the rigid 5-membered ring is unable to rotate to accommodate the repulsions.
The MOPAC results show very little difference in the energy of the isomers so it is not a good method to use for the minimisation of energy in this example. Therefore the structures from the MM2 calculations will be submitted for NMR.
 |
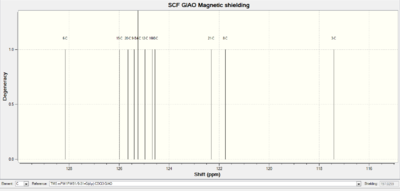 |
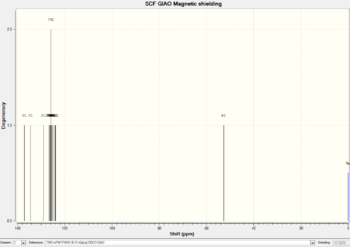 |
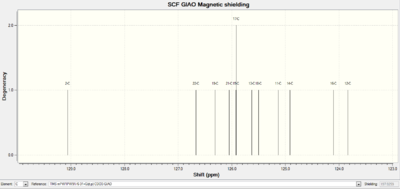 |
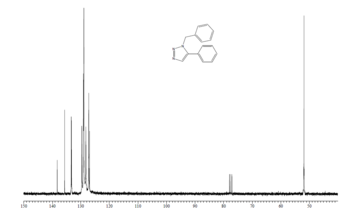 |
The regions of the NMR spectra which are unclear (around 130-110ppm for both spectra) are expanded so the individual peaks can be seen. The NMR output files were examined in Gaussian and the NMR peaks assigned to each carbon as seen in the table below. The diagrams above show that the spectra of Isomer B and the reference Isomer B look very similar, however, there are some peaks on the spectrum of Isomer A which match closely to the reference spectrum. The triplet peak at about 77.5ppm on the reference spectrum is due to the CDCl3 solvent.
 |
| Chemical Shift (ppm) | ||||
|---|---|---|---|---|
| Carbon Number | Triazole Isomer A | Literature Triazole A | Triazole Isomer B | Literature Isomer B |
| 1 | 117.42 | 120.1 | 129.06 | 133.34 |
| 2 | 145.29 | 148.0 | 137.11 | 138.26 |
| 3 | 128.15 | 130.7 | 125.13 | 128.22 |
| 4, 8 | 122.31, 121.75 | 125.7 | 125.93, 126.67 | 129.08 |
| 5, 7 | 125.65, 125.40 | 128.7 | 125.50, 126.05 | 128.92 |
| 6 | 124.57 | 128.1 | 126.31 | 133.26 |
| 9 | 55.31 | 41.0 | 52.68 | 51.85 |
| 10 | 133.65 | 135.0 | 134.54 | 135.66 |
| 11, 15 | 124.67, 124.97 | 128.2 | 124.10, 123.83 | 126.93 |
| 12, 14 | 125.99, 125.25 | 128.9 | 125.92, 125.62 | 129.64 |
| 13 | 125.25 | 129.1 | 124.91 | 127.22 |
The results of the 13C NMR spectrum show there is good correlation between the spectrum obtained for isomer B and the literature spectrum with the majority of chemical shifts being about 3-4ppm apart. This difference is due to the method of calculation and because spin-orbit coupling is not taken into account. There are no carbonyl carbons in the molecule and the rings are aromatic with no fixed double bonds so corrections to the chemical shifts do not need to be applied.
Computational methods for the determination of NMR do not take into account the aromaticity of the rings in the molecule so although there are 11 different carbon environments in both isomers, the computer gives a peak for each carbon atom so the spectrum shows 15 carbon peaks in total. It takes the π-electrons to be fixed in the double bonds instead of delocalised about the rings and this also contributes to the difference in chemical shifts between the calculated and reference spectra.
The only carbon in molecule B which shows a great deviation from the literature chemical shift is carbon 6. The difference in chemical shifts for this carbon is 6.95ppm. The reason for this is not known as when the structure of the molecule was changed and MM2 calculations were run, the molecule either reverted back to the structure submitted for NMR or was higher in energy than before.
The NMR data for isomer A is much less similar to the literature spectrum than B with the greatest difference in chemical shift resulting from carbon 1 (a difference of 15.92ppm). This may be due to the presence of the phenyl group on the nitrogen atom adjacent to carbon 1. Therefore the NMR data for B is a much better fit to the literature NMR from the reference given.
Literature NMR data was also found for isomer A[3] however, the paper did not assign the 13C peaks and did not provide a spectrum so the peaks had to be assigned according to how they were assigned in Gaussian. Most of the chemical shifts from the calculated NMR for A fit well with the literature values with the exception of carbon 9 which was found to be 14.31ppm more than in the literature. This may be because the orientation of the phenyl group attached to carbon 9 is wrong.
The 1H NMR can also be found using Gaussian:
 |
 |
 |
The spectra show that the 1H NMR for isomers A and B are quite similar and show that the computational methods for NMR do not consider the equivalent chemical environments of some protons on the aromatic rings. Therefore they assign each individual proton a peak instead of grouping chemically equivalent protons together. The 3JH-H coupling constants could be calculated using the Karplus equation (8.5cosθ2-0.28) however, this would have little effect in aiding the assignment of the isomers.
IR can also be used to tell the isomers apart as they should give different peaks due to different bond vibrations in the molecules.
 |
 |
The IR spectra of the isomers are quite different in the region of 0-500cm-1 due to the twisting of the aromatic rings in relation to each other. The IR spectrum for isomer B shows more peaks than for A because there are more bond vibrations as it is higher in energy than A. This is because isomer B has less flexibility than isomer A as the benzyl and phenyl groups clash due to sterics.
References and Citations:
- ↑ G.A. Wallace, T.D. Gordon, M.E. Hayes,D.B. Konopacki, S.R.Fix-Stenzel, X. Zhang, P. Grongsaard, K.P. Cusack, L.M. Schaffter, R.F. Henry and R.H. Stoffer, J. Org. Chem., 2009, 74 (13), 4886-4889DOI:10.1021/jo900376b
- ↑ L. Zhang, X. Chen, P. Xue, H.H.Y. Sun, I.D. Williams, K.B. Sharpless, V.V. Fokin and G. Jia, J. Am. Chem. Soc., 2005, 127(46), 15998-15999 DOI:10.1021/ja54114
- ↑ L. Campbell-Verduyn, L.Mirfeizi, R.A. Dierckx, P.H. Elsinga and B.L. Feringa, Chem. Commun., 2009, 2139-2141 DOI:10.1039/B822994E Supplementary Material [1]
Conclusions
From the questions and the mini-project investigated, it can be seen that computational methods provide an easy way to analyse and compare stereo- and regioisomers if they are interconvertable. NMR, IR and properties of the bonds in the molecules can be calculated and compared to literature values. This is very beneficial as it allows scientists to do calculations in a short amount of time and with, in general, reliable results. However, computational methods can not replace chemical intuition so molecules must sometimes be adjusted in order to obtain the optimum conformation. This also applies to analysis of the NMR spectra as the computer does not account for equivalency between atoms because it does not operate using the normal NMR time scale.











