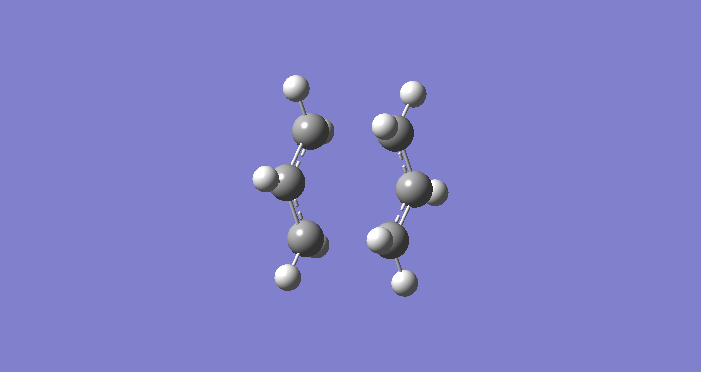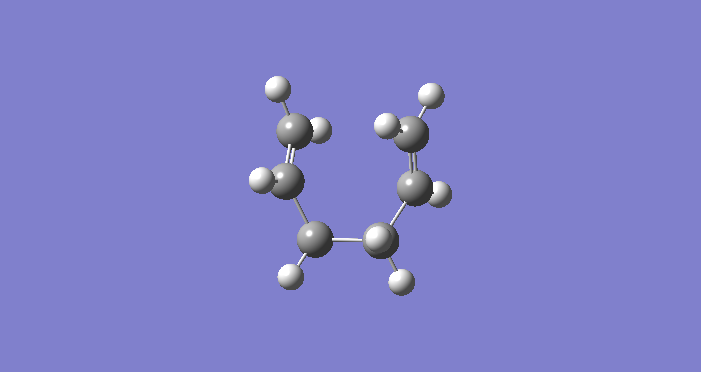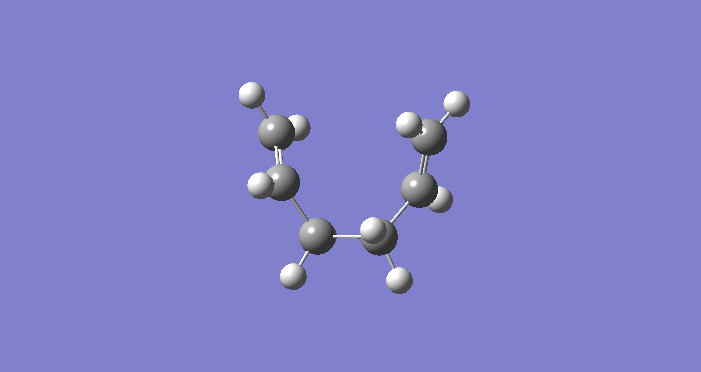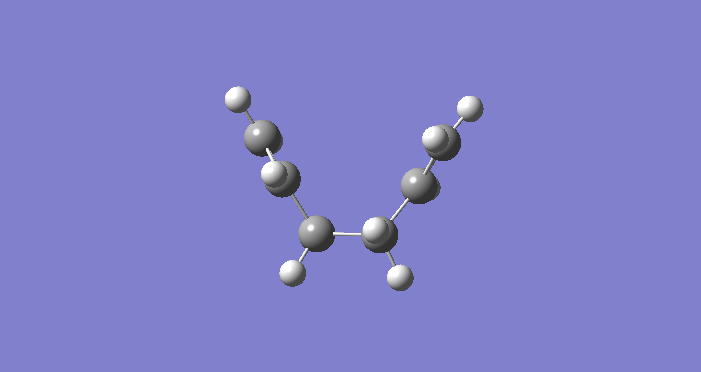Rep:Mod:PAHPhysical156
The Cope Rearrangement
Introduction
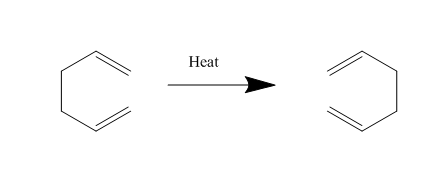
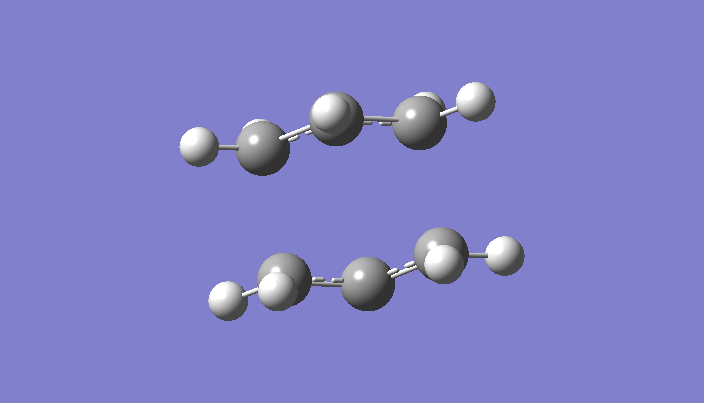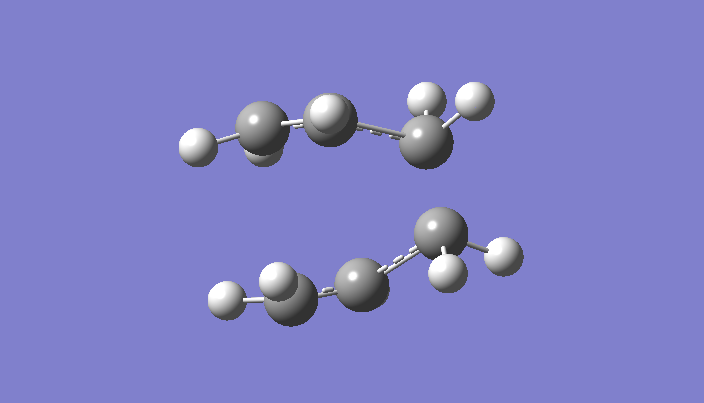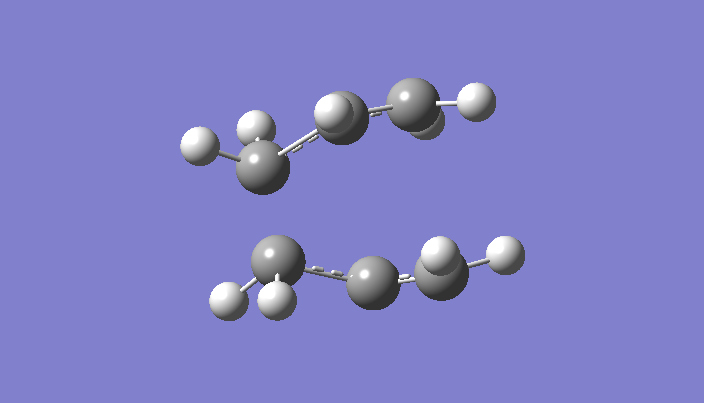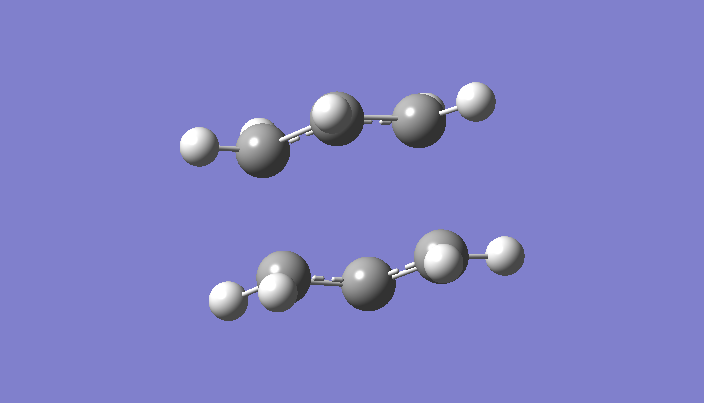
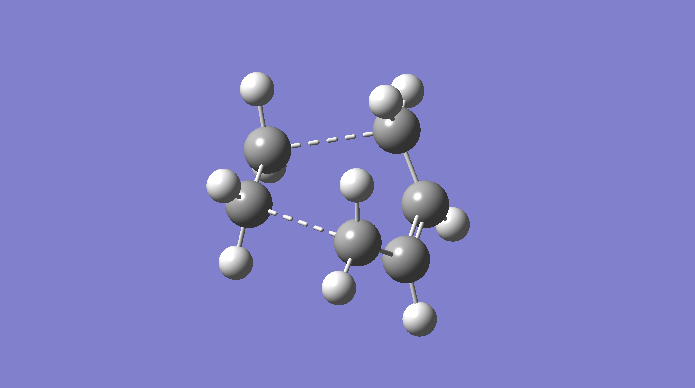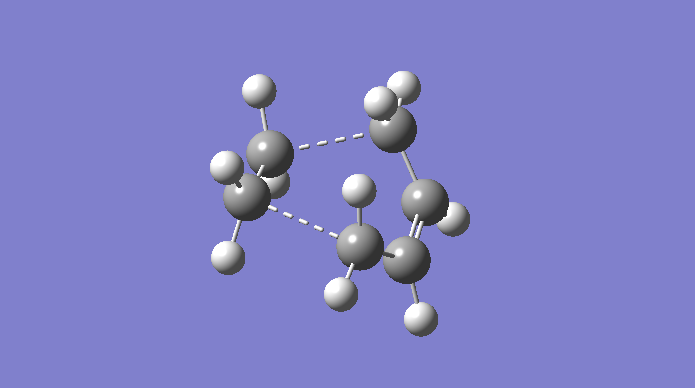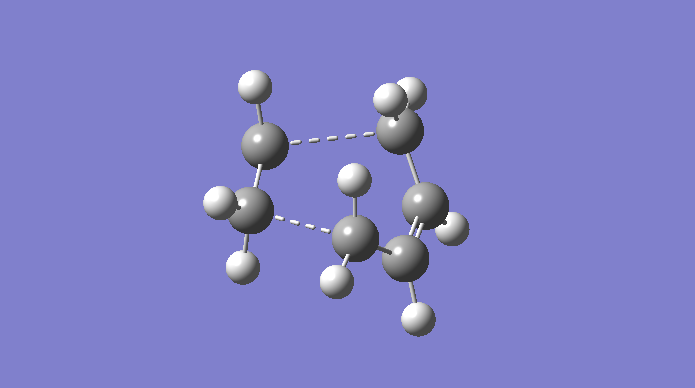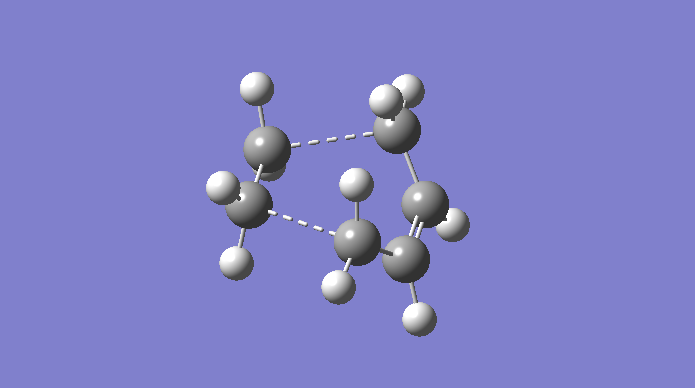
The Cope rearrangement is a famous example of a [3,3]-sigmatropic pericyclic reaction, and we are concerning ourselves with the reaction in 1,5-hexadiene. The mechanism is a concerted pericyclic process, and can pass through two separate (aromatic) transition states, based on boat and chair structures. We shall see more of this later. The Cope rearrangement we are dealing with is:
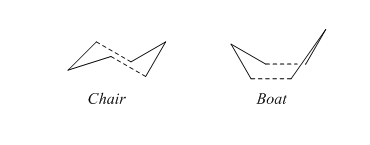
The transition structures through which this mechanism can proceed are shown here.
By using Gaussian, we aim in this exercise to elucidate the accurate geometries of transition states, the energies associated with them and the molecular orbital situations. The first computations will be run using relatively simple methods and basis sets, but more complex (and thus more accurate) ones will be used later, particularly with the second assignment on full Diels-Alder reactions.
Optimising the reactants and products
Let us start the proceedings by undertaking an optimisation on a molecule of anti-hexadiene. In the first instance we will use a relatively simple method and basis set, namely Hartree-Fock 3-21G. The key results of this optimisation (including the point group) are given here:
| Category | Answer |
|---|---|
| File type | .chk |
| Calc. type | FOPT |
| Calc. method | RHF |
| Basis set | 3-21G |
| Final energy | -231.69260235 a.u. |
| Gradient | 0.00001824 a.u. |
| Dipole moment | 0.2021 D |
| Point group | C2 |
| Comp. time | 48 seconds |
| Log file | Click here |
The text below contains the useful data given in the log file, telling us that the optimisation converged and was completed. This is, as we shall see later, only half of the issue; a frequency analysis is required to determine the nature of our stationary point.
Item Value Threshold Converged? Maximum Force 0.000056 0.000450 YES RMS Force 0.000010 0.000300 YES Maximum Displacement 0.001507 0.001800 YES RMS Displacement 0.000459 0.001200 YES Predicted change in Energy=-2.090938D-08 Optimization completed. -- Stationary point found.
Now that we have performed an optimisation on an anti-periplanar arrangement, we can run an optimisation on a gauche structure. We can expect the gauche conformation to have a higher energy due to either the steric hindrance resulting from the substituents or due to hyperconjugation into correctly aligned antibonding orbitals. This is indeed corroborated in the data below, note the energy is higher. The relevant section of the log file is again copied below for understanding.
| Category | Answer |
|---|---|
| File type | .chk |
| Calc. type | FOPT |
| Calc. method | RHF |
| Basis set | 3-21G |
| Final energy | -231.69166702 a.u. |
| Gradient | 0.00000609 a.u. |
| Dipole moment | 0.3804 D |
| Point group | C2 |
| Comp. time | 2 mins 3.4 seconds |
| Log file | Click here |
Item Value Threshold Converged? Maximum Force 0.000176 0.000450 YES RMS Force 0.000038 0.000300 YES Maximum Displacement 0.001331 0.001800 YES RMS Displacement 0.000386 0.001200 YES Predicted change in Energy=-1.789149D-08 Optimization completed. -- Stationary point found.
We can now perform more optimisations on different conformers to analyse any differences in energies. The basis set remains the same at all times, else comparison of energies would be meaningless. Below, we have located the anti2 conformation; our energy value is similar to the value provided in the script (-231.69254 a.u.), and we have obtained the correct structure.
| Category | Answer |
|---|---|
| File type | .chk |
| Calc. type | FOPT |
| Calc. method | RHF |
| Basis set | 3-21G |
| Final energy | -231.69253528 a.u. |
| Gradient | 0.00001339 a.u. |
| Dipole moment | 0.0003 D |
| Point group | Ci |
| Comp. time | 48.6 seconds |
| Log file | Click here |
Item Value Threshold Converged? Maximum Force 0.000021 0.000450 YES RMS Force 0.000006 0.000300 YES Maximum Displacement 0.001285 0.001800 YES RMS Displacement 0.000348 0.001200 YES Predicted change in Energy=-2.283098D-08 Optimization completed. -- Stationary point found.
So far, we have been using only a relatively simple basis set to perform our optimisations. We shall now change to a more complex set in order to achieve a more accurate result (though at the cost of greater computing time). The method and basis set we will be using are DFT, B3LYP with a 6-31G(d) (also referred to as 6-31G*) basis set. The results are presented here:
| Category | Answer |
|---|---|
| File type | .chk |
| Calc. type | FOPT |
| Calc. method | DFT |
| Basis set | 6-31G(d) |
| Final energy | -231.61171035 a.u. |
| Gradient | 0.00001360 a.u. |
| Dipole moment | 0.0000 D |
| Point group | C1 |
| Comp. time | 4 mins 15.8 secs |
| Log file | Click here |
Item Value Threshold Converged? Maximum Force 0.000016 0.000450 YES RMS Force 0.000007 0.000300 YES Maximum Displacement 0.000263 0.001800 YES RMS Displacement 0.000088 0.001200 YES Predicted change in Energy=-1.674888D-08 Optimization completed. -- Stationary point found.
We have now optimised our molecule using a reasonable basis set, and it has reached a stationary point. As mentioned earlier, however, we have no way at this point to determine the nature of the stationary point - to elucidate this, we can run a frequency analysis. This must be done with the same basis set and method, otherwise the results become meaningless. The low frequencies are provided below: none of the second row are negative frequencies, therefore we know we have reached a minimum. If one is negative (imaginary), we have obtained a transition state; if there are more than one, the optimisation did not complete and we have encountered an error. The log file for this analysis can be found by clicking here.
Low frequencies --- -9.4870 -0.0010 -0.0008 -0.0006 3.7345 13.0055 Low frequencies --- 74.2858 80.9992 121.4169
This is not the limit of the benefits gained by running a frequency analysis; we can also gain a considerable amount of useful thermochemical data about our molecule in question. In isolation these data mean nothing, but taken with other conformations optimised using the same methods and basis set, we can compare energies and draw conclusions from them. A selection of these is given in the table below.
| Category | Value |
|---|---|
| Sum of electronic and zero-point energies | -234.469204 |
| Sum of electronic and thermal energies | -234.461857 |
| Sum of electronic and thermal enthalpies | -234.460913 |
| Sum of electronic and thermal free energies | -234.500777 |
A frequency analysis provides a list of vibrational modes available to the molecule (including imaginary frequencies and IR-inactive motions!). These can be animated in GaussView, and we shall see some of these later.
The chair and boat structures
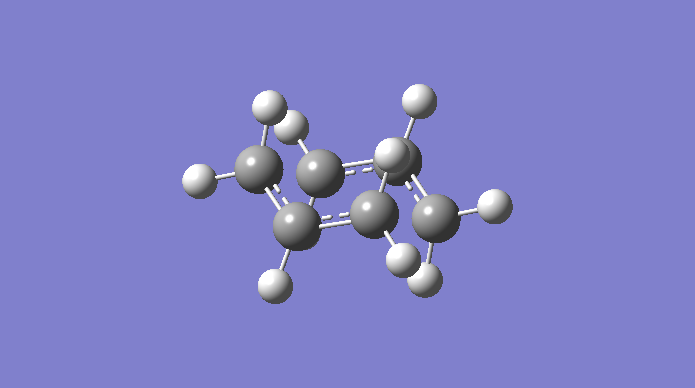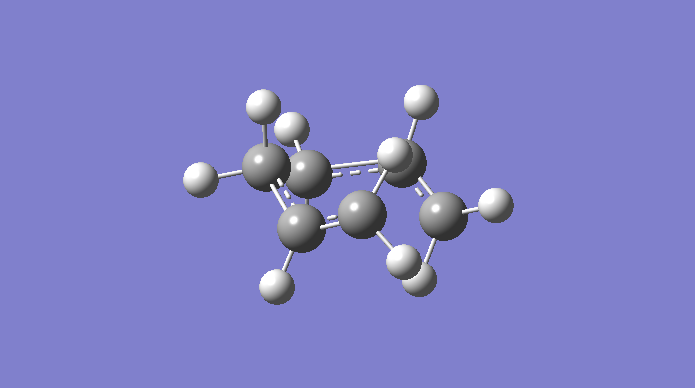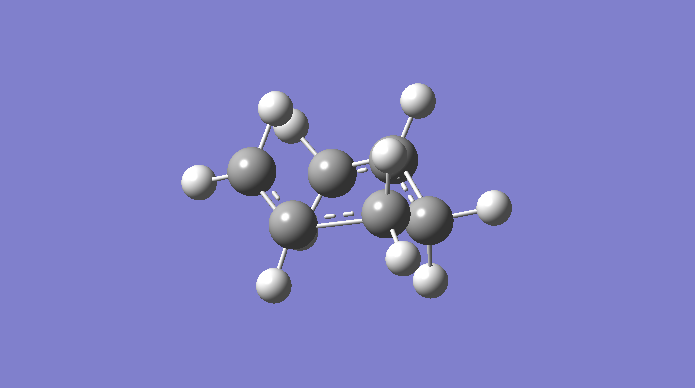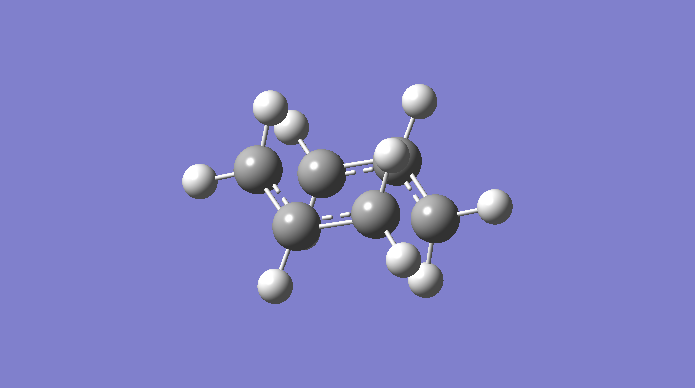
In the previous section we concerned ourselves with optimisations to a minimum; certainly useful, but they provide little insight into the mechanism of a reaction. This can be explored through optimising to a transition state, and some commonly used methods to achieve this will be discussed in this section. We shall start by forming a rough guess of our boat transition state by using two allyl fragments arranged in space in an approximately correct way. The first transition state method used will be the Whole Hessian approach, using the optimisation to a TS (Berny) option in Gaussian. For this section, we will be using a relatively simple HF/3-21G method and basis set. The allyl fragment is optimised before being copied and manoeuvred into position.
Now that the fragments are in position, we can run and optimisation and a frequency analysis in one computation. The results of this are provided.
| Category | Answer |
|---|---|
| File type | .log |
| Calc. type | FOPT |
| Calc. method | RHF |
| Basis set | 3-21G |
| Final energy | -231.61932240 a.u. |
| Gradient | 0.00001578 a.u. |
| Dipole moment | 0.0008 D |
| Point group | C1 |
| Comp. time | 20.5 seconds |
| Log file | Click here |
This computation yields an imaginary frequency in the list of vibrations: this is the animation of the Cope rearrangement as seen here:
Our next method to find the transition state structure is the frozen coordinate method, which allows us to precisely define the arrangement of the atoms in the molecule. The results of this method are provided here.
| Category | Answer |
|---|---|
| File type | .log |
| Calc. type | FOPT |
| Calc. method | RHF |
| Basis set | 3-21G |
| Final energy | -231.63013427 a.u. |
| Gradient | 0.00957406 a.u. |
| Dipole moment | 0.0930 D |
| Point group | C1 |
| Comp. time | 1 minute 43.0 seconds |
| Log file | Click here |
Following this, we obtain a structure similar to our previously found structure, but the bond distances are fixed. We can now optimise the molecule to find correct values for the bond distances. The result of this optimisation is shown below.
| Category | Answer |
|---|---|
| File type | .log |
| Calc. type | FOPT |
| Calc. method | RHF |
| Basis set | 3-21G |
| Final energy | -231.61932232 a.u. |
| Gradient | 0.00003582 a.u. |
| Dipole moment | 0.0009 D |
| Point group | C1 |
| Comp. time | 1 minute 1.3 seconds |
| Log file | Click here |
Let us now compare the bond distances in the transition structures we have obtained so far. As can be seen, both methods provide similar values, though the Berny optimisation yields a slightly larger value for each distance.
| Bond | Berny TS | Frozen Coordinate |
|---|---|---|
| C-C 1 | 2.02077 | 2.02038 |
| C-C 2 | 2.02068 | 2.02043 |
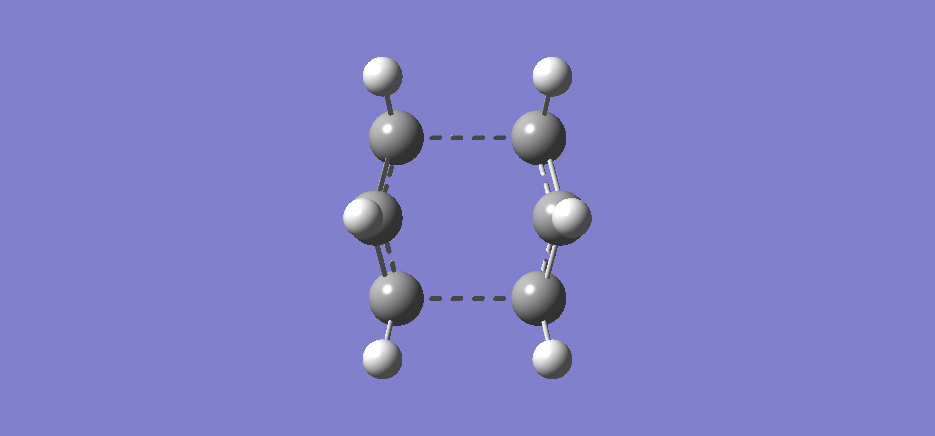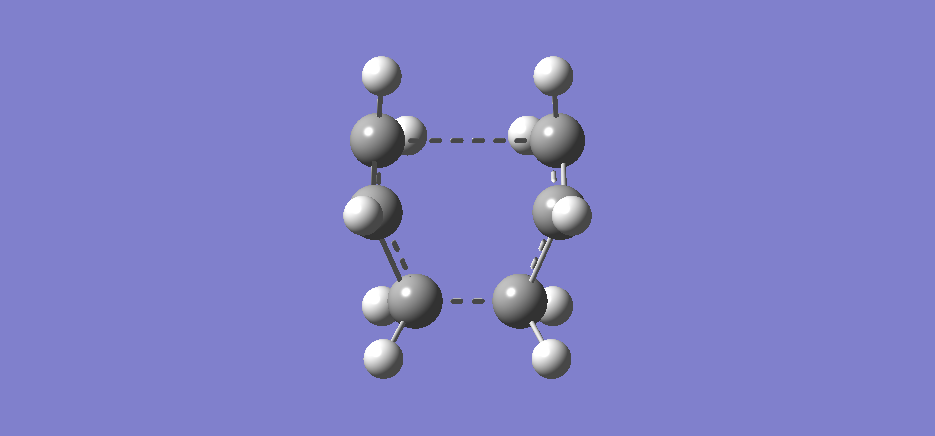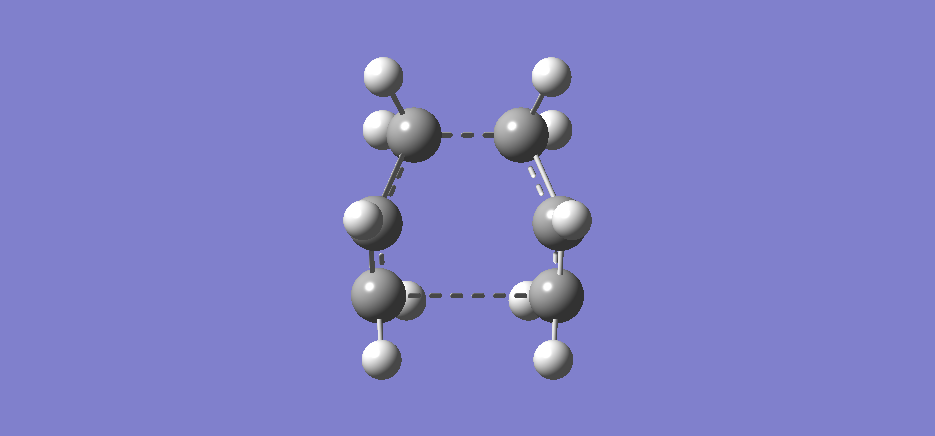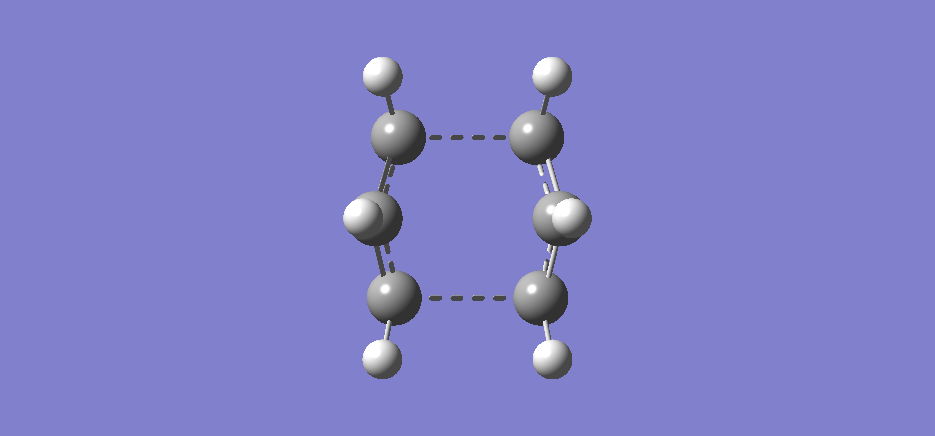
The Boat transition state
We have thus far obtained the chair structure, but not the boat structure. This we shall do now. Using the anti2 structure obtained earlier, we can arrange this and optimise it to a transition state, this time using QST2. The atoms are labelled and arranged in space in an arrangement we would expect from a transition state. The first attempt, however, is a failure - the structure given looks more like a chair transition state! This is due to the fact that Gaussian simply translates the fragments without considering other factors, such as rotation about the central bonds in the fragments. This is animated here.
We thus set up our input with more conditions - the central dihedral angle is set to zero, while the inside C-C-C bonds are set to 100°. We can then run the QST2 calculation again, which yields the data below:
| Category | Answer |
|---|---|
| File type | .log |
| Calc. type | FOPT |
| Calc. method | RHF |
| Basis set | 3-21G |
| Final energy | -231.60280247 a.u. |
| Gradient | 0.00004118 a.u. |
| Dipole moment | 0.1582 D |
| Point group | C1 |
| Comp. time | 21 seconds |
| Log file | Click here} |
Below is the animation from the imaginary frequency (-839.97cm-1) provided by the computation, viewed from beneath. Note that unlike in the chair structure, the two carbon atoms in the "middle" are pointing the same direction as is expected in the boat structure.
Item Value Threshold Converged? Maximum Force 0.000094 0.000450 YES RMS Force 0.000018 0.000300 YES Maximum Displacement 0.001205 0.001800 YES RMS Displacement 0.000345 0.001200 YES Predicted change in Energy=-1.730162D-08 Optimization completed. -- Stationary point found.
The Intrinsic Reaction Coordinate (IRC) method
We can determine the nature of the transition state easily enough, but this gives us no clue about the conformer resulting from a particular transition state structure. The IRC method allows us to determine these by following the potential energy surface down to a local minimum - for this example we shall use our pre-optimised chair structure. We will run this calculation with 50 steps, and the results of this are shown here.

| Category | Answer |
|---|---|
| File type | .log |
| Calc. type | IRC |
| Calc. method | RB3LYP |
| Basis set | - |
| Final energy | -231.61932240 a.u. |
| Gradient | 0.00001578 a.u. |
| Dipole moment | 0.0008 D |
| Point group | C1 |
| Comp. time | 13 mins 32.7 seconds |
| Log file | Click here |
An animation of the process is also shown here.
This is adequate enough for our present requirements, but there are many extra procedures available to further enhance these results. It is possible to run a normal optimisation to a minimum on the last IRC step, or equally it is possible to run another IRC calculation with either more steps or calculation of the force constants at each step. The latter is rather expensive in terms of time and effort, though consequently it would be the most reliable. In this exercise, however, we shall leave IRC here for the time being.
A more complex basis set
We have now obtained geometries for our transition structures, but not the relevant energy data. We can calculate the activation energies for the reaction pathways by optimising the transition states and reactant using the same basis set. In this instance, we are using B3LYP/6-31G(d) - a more complex basis set, it provides similar geometries but considerably different (and more accurate!) energy values. The results of the optimisations are provided below, and frequency analyses were run on each in turn to provide the thermochemistry data.
| Category | Answer |
|---|---|
| File type | .log |
| Calc. type | FREQ |
| Calc. method | RB3LYP |
| Basis set | 6-31G(d) |
| Final energy | -234.55698295 a.u. |
| Gradient | 0.00003094 a.u. |
| Dipole moment | 0.0003 D |
| Point group | C1 |
| Comp. time | 5 mins 24.4 seconds |
| Log file | Click here |
Item Value Threshold Converged? Maximum Force 0.000053 0.000450 YES RMS Force 0.000015 0.000300 YES Maximum Displacement 0.001085 0.001800 YES RMS Displacement 0.000323 0.001200 YES Predicted change in Energy=-1.618474D-07 Optimization completed. -- Stationary point found.
The boat structure:
| Category | Answer |
|---|---|
| File type | .log |
| Calc. type | FREQ |
| Calc. method | RB3LYP |
| Basis set | 6-31G(d) |
| Final energy | -234.54309304 a.u. |
| Gradient | 0.00001210 a.u. |
| Dipole moment | 0.0615 D |
| Point group | C1 |
| Comp. time | 6 minutes 26.3 seconds |
| Log file | Click here |
Item Value Threshold Converged? Maximum Force 0.000026 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000724 0.001800 YES RMS Displacement 0.000221 0.001200 YES Predicted change in Energy=-1.406636D-08 Optimization completed. -- Stationary point found.
The optimisation of the reactant:
| Category | Answer |
|---|---|
| File type | .log |
| Calc. type | FREQ |
| Calc. method | RB3LYP |
| Basis set | 6-31G(d) |
| Final energy | -234.61171035 a.u. |
| Gradient | 0.00001359 a.u. |
| Dipole moment | 0.0000 D |
| Point group | C1 |
| Comp. time | 5 minutes 2 seconds |
| Log file | Click here |
Item Value Threshold Converged? Maximum Force 0.000021 0.000450 YES RMS Force 0.000006 0.000300 YES Maximum Displacement 0.001285 0.001800 YES RMS Displacement 0.000348 0.001200 YES Predicted change in Energy=-2.283098D-08 Optimization completed. -- Stationary point found.
The data gained from these optimisations can now be compared (since we are using the same basis set), and are presented in this table.
| HF/3-21G | B3LYP/6-31G(d) | |||||
|---|---|---|---|---|---|---|
| Electronic energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | Electronic energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | |
| Temperature | At 0 K | At 298.15 K | At 0 K | At 298.15 K | ||
| Chair TS | -231.61932240 | -231.466701 | -231.461341 | -234.55698295 | -234.414932 | -234.409011 |
| Boat TS | -231.60280247 | -231.450928 | -231.445299 | -234.54309304 | -234.402342 | -234.396008 |
| Reactant (anti2) | -231.69253528 | -231.539540 | -231.532566 | -234.61171035 | -234.469204 | -234.461857 |
| HF/3-21G | B3LYP/6-31G(d) | |||
|---|---|---|---|---|
| At 0 K | At 298.15 K | At 0 K | At 298.15K | |
| ΔE Chair | -45.71 | -44.694 | -34.06 | -33.16 |
| ΔE Boat | -55.60 | -54.76 | 41.95 | 41.32 |
Our values bear good agreement with the experimental values provided by the script, namely 33.5 ± 0.5 kcal/mol for the chair at 0 K and 44.7 ± 2.0 kcal/mol for the boat at 0 K. [1]
Diels-Alder reactions: second week
Using what we have learned in the exercises so far, we will now apply these techniques to systems involving the Diels-Alder cycloaddition. Using Gaussian, we will compute transition structures where appropriate and examine the molecular orbitals of the systems, allowing us to comment upon the mechanism of the reaction and the reasons behind such a mechanism. The first example we will use is relatively simple, cis-butadiene.
cis-butadiene
The method used in this section involves optimising the molecule on one basis set first (HF/3-21G) followed by a second optimisation using a more complex basis set. This gives reliable results and is not overly expensive to run. The results of these optimisations are displayed below.
| Category | Answer |
|---|---|
| File type | .log |
| Calc. type | FOPT |
| Calc. method | RB3LYP |
| Basis set | 3-21G |
| Final energy | -155.13489510 a.u. |
| Gradient | 0.00002293 a.u. |
| Dipole moment | 0.0474 D |
| Point group | C1 |
| Comp. time | 1 minute 1.2 seconds |
| Log file | Click here |
| Category | Answer |
|---|---|
| File type | .log |
| Calc. type | FOPT |
| Calc. method | RB3LYP |
| Basis set | 6-31G(d) |
| Final energy | -155.98594952 a.u. |
| Gradient | 0.00006144 a.u. |
| Dipole moment | 0.0852 D |
| Point group | C2 |
| Comp. time | 38.1 seconds |
| Log file | Click here |
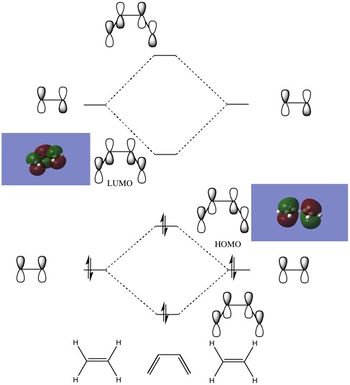
A brief sketch of the MO diagram of this molecule is shown here, followed by images of the HOMO/LUMO in the table.
| HOMO | LUMO |
|---|---|
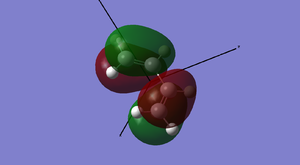 Antisymmetric Antisymmetric |
 Symmetric Symmetric
|
Butadiene + ethylene Diels Alder
The optimised molecule of butadiene can now be put to use in a reaction with ethylene. An optimisation and a frequency analysis are carried out, yielding the data and animation below. The frequency analysis confirmed we have reached the transition state, since one imaginary frequency was present in the "low frequencies".
| Category | Answer |
|---|---|
| File type | .log |
| Calc. type | FREQ |
| Calc. method | RB3LYP |
| Basis set | 6-31G(d) |
| Final energy | -234.54389655 a.u. |
| Gradient | 0.00000890 a.u. |
| Dipole moment | 0.3945 D |
| Point group | C1 |
| Comp. time | 6 minutes 23.3 seconds |
| Log file | Click here |
A sketch of the transition state is given here, along with values for the bond distances.
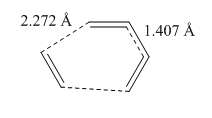
| Computation | Literature | |
|---|---|---|
| C-C σ bonds being formed | 2.272 | 2.27 |
| C2-C3 bond (new double bond) | 1.407 | 1.41 |
The values obtained by computation means offer a good agreement with literature values - we can thus confirm our computational method is valid.[2] Let us now consider these bond lengths in relation to other carbon-carbon bond lengths; a typical sp3-sp3 bond length is 1.54Å, while a typical sp2-sp2 is 1.47Å.[3] We can see from our data that the values in the transition state, particularly the length of the soon to be formed double bond, that our values are not close, but not far away either. This is to be expected from a transition state; after all, the molecule has yet to fully take shape. The Van der Waals radius of a carbon atom is 1.70 Å, hence the "diameter" is 3.40 Å - well above the length of the forming bonds, so the bonds are easily made with not too much shift in geometry.[4]
Note from this animation that the formation of the new σ-bonds is synchronous - this reaction involves symmetric reactants and the "curly arrows", if drawn, could proceed either way around the system. Let us now compare this vibration with the lowest positive frequency (135.77 cm-1).
In this vibration the C-C bond formation is asynchronous - this is the result of two reaction mechanisms that are proposed to exist:
- There is a symmetric and synchronous concerted pericyclic mechanism whereby both bonds are formed simultaneously - this is the example shown by the imaginary frequency.
- There is also a non-concerted, asynchronous mechanism involving a di-radical transition state in which one bond is formed ahead of the other.
The real situation is somewhere in between - elements of both mechanisms are present in the reaction and can result in bond distance differences between the two new bonds. Let us now examine the molecular orbitals of the reactants and transition state in more detail.
The HOMO of the transition state structure is symmetric with respect to the plane; which MOs of the reactants have come together to form this? Upon inspection, we can see that the HOMO has been formed from the combination of the ethylene LUMO and the butadiene HOMO. This is allowed as we are adding together two antisymmetric orbitals and resulting in a symmetric orbital.
Diels-Alder
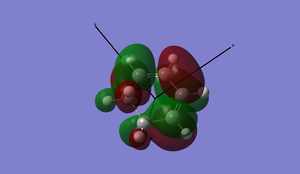
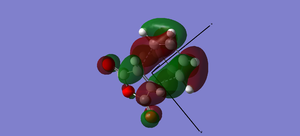
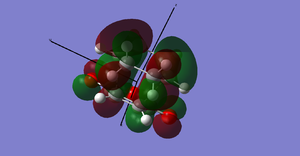
| Category | Maleic anhydride | Cyclohexadiene | Exo | Endo |
|---|---|---|---|---|
| Picture |  |
 |
 |
|
| File type | .log | .log | .log | .log |
| Calc. type | FOPT | FOPT | FREQ | FREQ |
| Calc. method | RB3LYP | RB3LYP | RB3LYP | RB3LYP |
| Basis set | 6-31G(d) | 6-31G(d) | 6-31G(d) | 6-31G(d) |
| Final energy | -379.28954412 a.u. | -233.41891071 | -612.67931096 | -612.68339676 |
| Gradient | 0.00011730 a.u. | 0.00003451 | 0.00000719 | 0.00001402 |
| Dipole moment | 4.0749 D | 0.3780 D | 5.5501 | 6.1144 |
| Point group | CS | C2 | C1 | C1 |
| Comp. time | 2 minutes 43.2 seconds | 2 minutes 38.1 seconds | 26 minutes 26.3 seconds | 31 minutes 30.6 seconds |
| Log file | Click here | Click here | DOI:10042/25979 | DOI:10042/25978 |
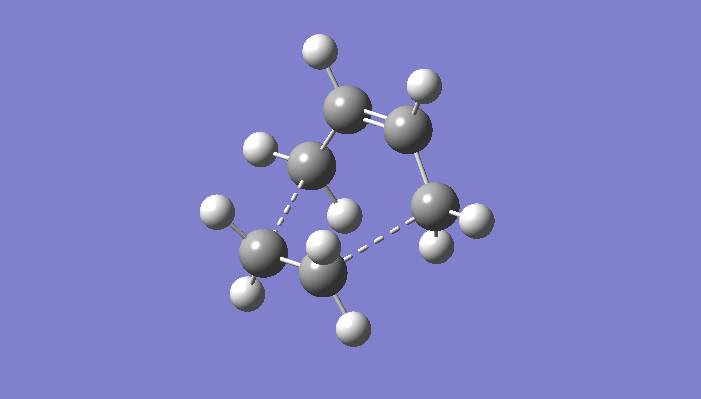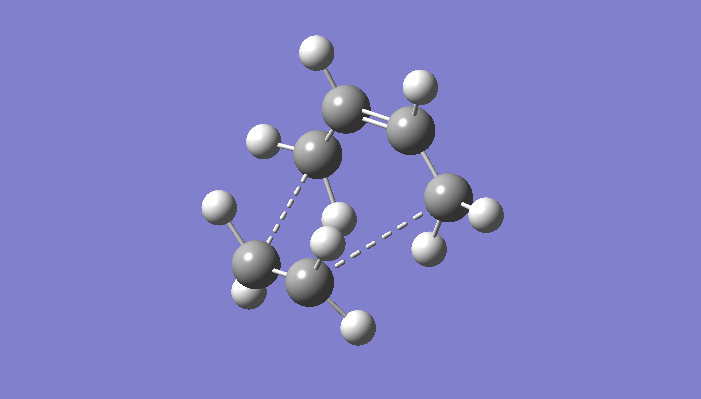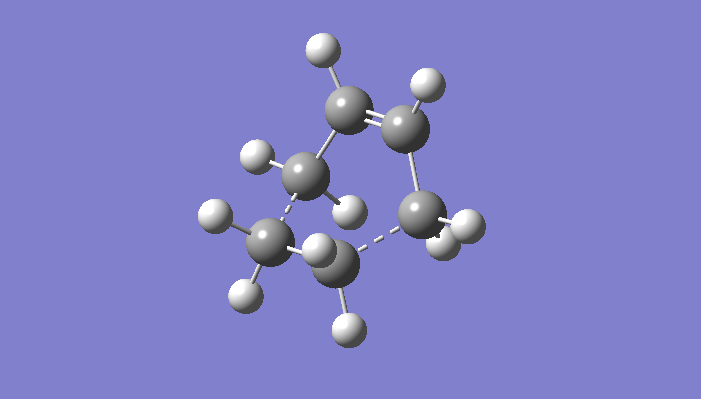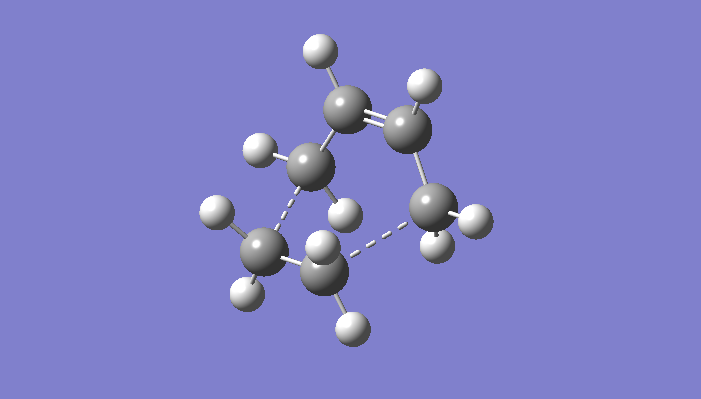
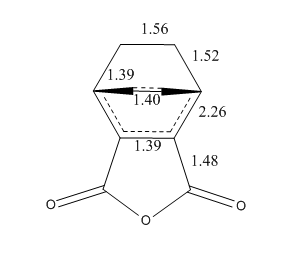
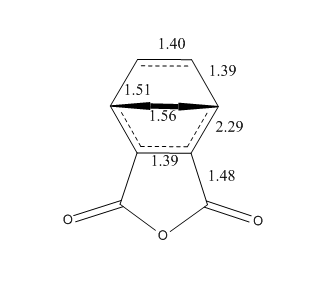
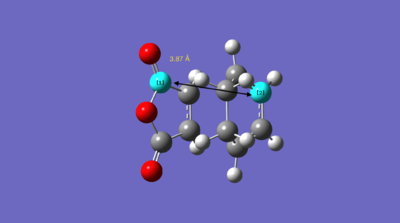
The energies of the endo/exo structures are displayed in the table - note that the exo product is noticeably higher in energy. This is as expected, since the endo structure is more stabilised by orbital reasons (we shall return to these later). The relevant bond distances are displayed on these sketches, on the left the endo product, on the right the exo product:
As can be seen, the bond distance of the newly-forming C-C σ-bonds differs slightly - the endo product has a shorter distances. This could be seen as an indication of the increased stability of the endo-product versus the exo product. We can also measure the throughspace distances of the molecule to determine which is the more closely packed (and, therefore, possibly more sterically hindered) product. These are 3.87Å and 3.94Å respectively.
These orbitals are solely those provided by the 6-31G(d) level of theory, but other basis sets and methods may provide different images of the MOs; the more complex the basis set, the more accurate the MO image. This accuracy, however, can frequently serve to make comprehension of the MO situation difficult, as the images bear less resemblance to our clear-cut LCAO theory.
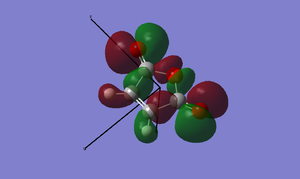
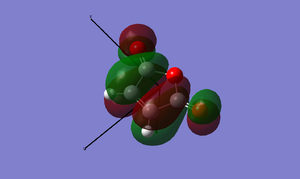
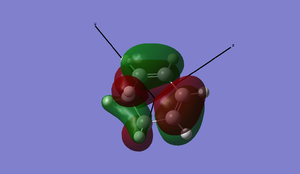
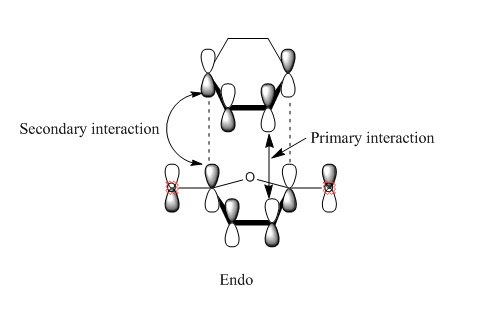
Now is a good time to return to an explanation of why endo-products are preferred over exo products. There are examples of Diels-Alder reactions favouring the exo product - if the endo product can easily dissociate back into the reactants, the thermodynamically favoured exo-product may result. This is of key importance when dealing with Diels-Alder reactions with sterically hindered systems. In our example, however, the endo product is the more stable: this is due to electronic effects, namely secondary orbital interactions, and a small strain effect. The diagrams below show what is happening with the two products.
In the case of the endo-structure, there are two primary interactions and two (weaker but still significant) secondary interactions with the carbonyl p-orbitals. For the exo-structure, these secondary interactions cannot take place as the range is too great to interact effectively. This is, however, the theory of the matter. In practice, if we look at the molecular orbitals provided by GaussView, we can see little evidence of secondary orbital interactions and indeed there is some debate over whether or not they really exist. An alternative suggests that in the exo structure, the hydrogens sticking out "over" the maleic anhydride group experience a degree of electrostatic repulsion from the positive carbonyl carbon atoms. This repulsion is not present in the endo-form, and may offer an explanation for this effect.[5]
The exo-structure is more strained since it has the -CH2CH2- fragment near the carbonyls, while the endo has only the -CH=CH- fragment. Having only one hydrogen on each carbon allows the hydrogen to move slightly to try to avoid steric clash, while the exo product with the two hydrogens per carbon does not allow this.
Conclusions
We have seen throughout these exercises that Gaussian is a powerful tool for elucidating a lot of information about a reaction pathway, its transition state and its energies. We have seen that there are many different ways to calculate transition structures, some considerably more accurate than others - yet this accuracy comes at a price of increased computation time. We have been able to extract some thermochemical data, for instance the activation energies, of certain reactions and their transitions states. This is most useful indeed: if we can predict computationally the activation energy of a reaction, we then have a much better knowledge of the necessary conditions of the reaction, should we wish to carry it out for real.
Different methods and basis sets can hugely influence the results of computations, sometimes considerably changing the geometries or energies of products/transition states. Additionally, changing the basis set affects to a great degree the molecular orbital situation in the molecule, be it in the shapes of the orbitals themselves or the ordering of their energies. This is important to remember, as we cannot be sure at any one time that our computations have provided the true "correct" answer - we merely have the answer according to that method.
Our examination of these molecules has been relatively simple, and it is important to note that we have neglected some important effects on the molecules. Primarily, we have not taken into consideration the effects of solvent on the transition states and reactions - depending on the solvent, this could have a significant effect in terms of energies and even geometries. Given more time, it would be sensible to repeat some of the calculations with the effects of solvents present; this would allow us to see reactions and structures under conditions more similar to those found in the lab.
Further study
This experiment has provided much useful data, but there is plenty more available to do; here is a list of some potential ways in which to explore the area further:
- The same principles behind this experiment (particularly relating to the Diels-Alder reactions) can be applied to larger and more complex situations - this could provide interesting data about more complex molecules, but could also lead to the emergence of trends between systems. These trends can only be verified by examining other molecular systems likely to contain such trends, and plotting the results.
- Similarly, the examples used in this experiment can be re-computed using different methods and basis sets. The results obtained may be more reliable, though will take more computing time. An interesting exercise would be to compare the results of three or four methods and basis sets on the molecular orbital situation, and in particular how they are ordered.
- We have looked only at the Cope rearrangement (a sigmatropic) and the Diels-Alder reaction (a cylcoaddition); we can also examine other pericyclic reactions. The same procedure can be applied to other reactions, and much interesting data may result.
- Finally, there is much debate yet to be had on the nature of secondary orbital interactions - and indeed upon their very existence. Further computational study in this area will prove invaluable in ascertaining the truth behind them.
References
- ↑ Physical Script, https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:phys3
- ↑ Dynamics, transition states, and timing of bond formation in Diels–Alder reactions, K. Black, Proceedings of the National Academy of Sciences Vol. 109 No. 32 DOI:10.1073/pnas.1209316109
- ↑ Fox, Marye Anne; Whitesell, James K. (1995). Organische Chemie: Grundlagen, Mechanismen, Bioorganische Anwendungen. Springer. ISBN 978-3-86025-249-9.
- ↑ http://reference.wolfram.com/mathematica/ref/ElementData.html
- ↑ Do Secondary Orbital Interactions Really Exist? J. Garciá, Acc. Chem. Res., 2000, 33 (10), pp 658–664 DOI:10.1021/ar0000152