Rep:Mod:PAHOrg156

Conformational analysis through the use of molecular mechanics

Diels-Alder products of cyclopentadiene dimerisation

The Diels-Alder reaction is a [4+2] cycloaddition reaction between a diene (specifically a diene in s-cis conformation) and a dienophile (normally an electron-poor alkene), and its effects are widespread and easily visible. The molecule of interest in this section is cyclopentadiene, notable for its ability to act as both diene and dienophile and hence react with itself (and indeed at room temperature, thus cyclopentadiene must be freshly "cracked" when used in the laboratory). The reaction yields two products, namely the endo and exo products; these names refer to the orientation of the molecules given by the required approaches. It is well known that the endo product is typically the major product in a Diels-Alder reaction, but this alone does not tell us much about the reaction: is the endo product the thermodynamic product (the most stable overall) or is it the kinetic product (the fastest formed)? This question can be answered comfortably enough using computational means; the most stable product will have the lowest calculated energy value.

This hypothesis can easily be examined (in this instance in Avogadro, though other software is available) by running optimisations on the two dimers using the MMFF94s force field, which has been designed to give a high degree of accuracy while also being valid when applied to larger molecules (e.g. biological molecules, proteins etc). The table below (Table 1) provides the energies calculated by these optimisations.

Energy (kcal/mol) Dimer 1 Dimer 2 Bond stretching energy 5.37 3.46 Angle bending energy 32.0 33.2 Torsional energy -2.79 -2.95 Van der Waals energy 14.2 12.3 Electrostatic energy 13.1 14.2 Total energy 55.4 58.2 Table 1

Dimer 1

Dimer 1

From the results, it is clearly seen that the endo product is of higher energy than the exo product - it can therefore be deduced that this is in fact the kinetic product. It would be wise at this point to discuss briefly the nature of a thermodynamically controlled reaction against a kinetically controlled reaction. Essentially, in a thermodynamic reaction, the most important factor is the energy of the products (indeed a kinetically formed product, if reversible, may reform into the thermodynamic product if given sufficient time); in a kinetically controlled reaction, the energy(ies) of the transition state(s) determine the outcome of the reaction. If the energy barrier to a transition state is too high , the system may sacrifice the gain in thermodynamic stability for the ease of the kinetic route. If the system is provided with more energy (i.e. heat), it would be expected that increasing amounts of the kinetic product will form: this is indeed the case . There are cases where the steric factors become significant, driving the balance towards the exo, but this is not one of them. To visualise these transition states, one may use a program like Gaussian - for our present purposes and for reasons of timekeeping, we shall not examine these in Gaussian. Instead, a cursory glance at the orbital situation may prove illuminating.

The orbital overlaps during the Diels-Alder reaction for both conformations

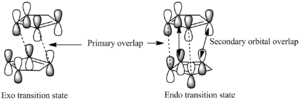
The orbitals which matter the most in the reaction are the HOMO and LUMO frontier orbitals - these are drawn in the diagram. It is clear to see in the image provided that the endo transition state offers more stability - the orbitals not directly involved in the bonding are nonetheless are in the right place and of the right symmetry such that a favourable interaction is noticed. In the exo case, no such interaction is possible, and consequently this transition state is more energetic. This is, however, a very simple approach to the problem and serves as a fleeting explanation of the phenomena at work here. There is, however, some debate about the nature of secondary orbital overlap effects, indeed some people have suggested they may not exist at all. This is merely a side note of interest; for the present time, it can be assumed they do exist and do affect the transition states as stated above.

The Hydrogenation of the endo-dimer

Having formed the endo-dimer above, the molecules can be partially hydrogenated such that one double bond in each dimer is saturated. The more readily hydrogenated double bond can be determined by optimising the structures of the products and comparing the energies - the process is the same as before (MMFF94s). This results in these data below in Table 2.

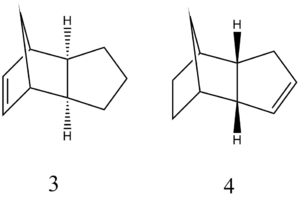
Hydrogenated dimers Energy (kcal/mol) Molecule 3 Molecule 4 Stretching energy 3.31 2.82 Angle bending energy 30.9 24.7 Torsional energy -0.071 -0.378 Van der Waals energy 13.3 10.6 Electrostatic energy 5.12 5.15 Total energy 50.7 41.3 Table 2

Dimer 1

Dimer 1

As can be clearly seen, structure 4 is the more stable of the two, with approximately one fifth less energy than structure 3; this result is supported by the literature, which claims that this product forms due to steric factors.

Atropisomerism of intermediates in the synthesis of Taxol

The structures numbered 9 and 10 (provided in the script) are those of two possible intermediates in the synthesis of Taxol; according to Paquette, the substituents on the cyclohexyl ring dictate which is preferred. These two molecules provide a fine example of atropisomerism, or expressed simply, isomers related by rotation about a single bond, though this rotation must possess a high energy barrier. One needs only take a perfunctory glance at the two structures to see why this energy barrier exists: the two ring structures joined together are not at all keen to rotate. Our goal in this exercise is to elucidate which of the two structures is the more stable by optimising the structures in Avogadro. It is highly possible that the first structure obtained will be a twist-boat, but this does not mean that a twist-boat is the most stable. It is commonly held that a chair structure is more stable than a boat or a twist boat, and while there are some exception, the general rule is valid here, and the chair structures are of lower energy.

One might ask: how can a supposed "minimsation" give different conformers? Let us consider for a moment what is happening. The optimisations are locating minimum points on the Potential Energy Surface (PES), but it is important to note that these do not necessarily correspond to a global minimum - they may only be local minima (consider the energy graph of standard cyclohexane ring shape changing - the local minima occupy one of the higher "valleys", while the global minima are to the side with the chair structure).

We have been able to elucidate four structures of Molecule 9, presented below. It is interesting to note that while two chair structures exist, one of them is of far higher energy than both twist boat structures - this is not what is expected of this conformation and clearly there must be more factors at work here. The "Chair 2" structure is more energetic by roughly 15 kcal/mol; most of this extra energy is from the angle bending energy and the electrostatic interactions. From this, it can be inferred that this structure is more strained, and that the carbonyl bond is playing a more significant role in distorting the electronics of the system. As it is, however, Chair 1 is the most stable form - this agrees with the theory.

Intermediate 9 Energy (kcal/mol) Chair 1 Chair 2 Twist-Boat 1 Twist-Boat 2 Bond stretching energy 7.17 7.87 7.38 7.98 Angle bending energy 23.1 32.0 24.0 31.8 Torsional energy 3.49 5.74 7.46 2.51 Van der Waals energy 33.1 36.0 35.0 36.7 Electrostatic energy 0.222 1.06 0.314 0.177 Total energy 67.7 83.6 74.9 80.3

Molecule 9 chair 1

Molecule 9 Chair 2

Molecule 9 Twist Boat 1

Molecule 9 Twist Boat 2

We can easily conduct the same procedure on Molecule 10, though this molecule seems to lack a second "twist boat" structure. Two chair structures and one twist boat structures were located by manipulation, yet despite repeated attempts, no second twist boat was located. From this we can conclude that such a structure is too energetic in comparison with the others - the more stable forms are preferred.

Intermediate 10 Energy (kcal/mol) Chair 1 Chair 2 Twist Boat 1 Bond stretching energy 8.18 7.87 8.41 Angle bending energy 26.9 32.0 27.6 Torsional energy 0.736 5.74 2.46 Van der Waals energy 35.3 36.0 36.8 Electrostatic energy 0.206 1.06 0.202 Total energy 70.6 83.6 76.2

Molecule 10 Chair 1

Molecule 10 Chair 2

Molecule 10 Twist-Boat 1

Thus we can compare the two structures, carbonyl up and carbonyl down. It can clearly be seen that in both molecules, angle bending plays a significant role in dictating the energy of the structure - consequently, we can use this to predict that the most stable structure is that which has bond angles closest to ideal conditions, particularly with respect to the carbonyl. Since the carbonyl carbon is sp², it much prefers to have an angle of 120°, and when this is not possible it adds significantly to the energy of the system.

Hyperstable olefins

It is observed in the lab materials that the alkenes reacted to functionalisation rather slowly - this is unexpected, as we know that alkenes are very keen to react, in part due to these reasons:

• The π-bond clouds are very accessible to incoming molecules and will readily take part in reactions
• The sp² hybridised carbons on either end of the alkene adopt a trigonal planar structure, which improves the steric situation around the atoms making them more accessible to attack.

Yet despite these factors, alkenes in these molecules (so-called bridgehead alkenes/olefins) suffer a high energy penalty when undergoing functionalisation. This energy penalty is primarily the result of a considerable increase in torsional strain - though surely we expect torsional strain to be alleviated by the functionalisation of a double bond? Normally, this is so, but in the cases of these molecules, where the bridgehead exists, greater molecular torsional strain is experienced through the removal of the planar alkene-bond. This effect is almost certainly a result of the cage-like structural features of these molecules, and it is doubtful that any significant electronic factors are relevant - after all, the electronics of the system favour functionalisation, not alkenes.

It would be an interesting experiment to compute the differences between alkene and alkane forms of certain molecules with bridgehead olefins. Indeed in the case of the Taxol intermediates, what would be the result if the double bond were moved to an alternative site in the molecule? If it were too far from the bridgehead and it would likely functionalise, so it would be useful to determine the general distances from a bridgehead at which an alkene becomes hyperstable and vice versa.

Spectroscopic analysis using quantum mechanics

The geometry of Structure 18 is given in the lab script from the paper by Paquette, and can be quickly optimised in Avogadro using the same force field as above (MMFF94s). Having optimised it, one can set up a Gaussian input file. Gaussian uses a different technique, ab initio Quantum Mechanics, to calculate various things about molecules. In this instance, we concern ourselves with predicted NMR spectra. The level of theory in use is the DFT/B3LYP with a 6-31G(d,p) basis set - this an accurate method, though time consuming. The NMR of Structure 18 is calculated thus; note it is also possible to work out spin coupling constants, but this takes a considerably greater amount of time. For our present purposes, they would be surplus to requirements and hence we shall pass over them, though if time is no object, they can be most useful indeed.

Molecule 18 Boat

Molecule 18 Chair

These images show the molecules after a preliminary optimisation in Avogadro; the following show the results after Gaussian optimisation. A list of NMR resulting from the calculations is provided below; all calculations have been recorded on D-space. From the Avogadro results, the

Structure 18 Energy (kcal/mol) Boat Chair Stretching energy 15.0 15.4 Angle bending energy 28.9 26.3 Torsional energy 13.4 10.37 Van der Waals energy 60.3 59.9 Electrostatic energy -8.42 -8.35 Total energy 105.1 104.0

Molecule 18 Boat (Gaussian)

Molecule 18 Chair (Gaussian)

The ¹³C NMR spectrum of Compound 18

¹³C NMR data for Molecule 18

Atom number	Calculated value (ppm)	Literature value (ppm)
15	211.83	211.49
4	148.66	148.72
5	118.84	120.90
24	89.09	74.61
7	67.89	60.53
18	56.12	51.30
3	55.60	50.94
19	50.11	45.53
42	48.19	40.82
43	44.23	38.73
25	42.03	36.78
14	37.59	35.47
27	35.31	30.84
6	31.05	30.00
28	28.85	25.56
21	25.73	25.35
2	25.26	22.21
20	23.40	21.39
26	21.06	19.83

As can be seen, the predicted carbon NMR peaks bear a reasonable resemblance to the literature values though there are some discrepancies. Apart from the expected slight differences, the chemical shifts of the carbons in the thioacetal group (nos. 42 and 43) are off by 6-8 ppm - this is caused by the presence of the nearby sulphurs. A correction factor is required to bring these values into line; such a factor could be very crudely applied using a separate optimised molecule based on the thioacetal, but unfortunately no time was available to calculate such a molecule and apply it. For this molecule, we need not worry unduly about the timescale issue (more on that later) - there are no possible issues relating to that due to the strict cage-ring structure.

The proton NMR spectrum of Compound 18

1H NMR data for Molecule 18 Atom number(s) Boat (ppm) Chair (ppm) 39 5.28 5.98 45 3.32 3.01 46 3.22 3.19 47 3.12 3.11 44 3.12 3.01 16 2.86 3.01 13 2.86 2.19 9 2.45 2.56 12 2.40 2.80 33 2.28 1.88 30 2.28 1.54 34 2.28 2.11 10 2.08 2.03 11 1.97 2.03 22 1.97 2.03 8 1.85 1.88 35 1.85 3.59 36 1.68 1.88 32 1.68 1.88 31 1.62 1.47 51 1.50 1.47 48 1.50 1.62 17 1.41 1.54 38 1.35 1.62 49 1.16 1.18 37 1.07 1.08 29 1.07 1.35 50 1.07 1.00 53 0.96 0.94 52 0.96 0.94

Proton NMR literature comparison Reported shift (ppm) Multiplicity/integration Possible atom nos. 5.21 m 1H 39 3.00-2.70 m 6H 42, 45, 46, 47 2.70-2.35 m 4H 9, 12, 33, 30 (or 42, 45, 46, 47 again) 2.20-1.70 m 6H 34, 10, 11, 22, 8, 35 1.58 t 1H 36 1.50-1.20 m 3H 31, 51, 48 1.10 s 3H 17, 38, 49 1.07 s 3H 37, 29, 50 1.03 s 3H 50-53

The predicted proton NMR presents a perplexing picture of the molecule, and assignment of particular hydrogens to match up with the literature is not trivial, since the literature concerns an experimentally determined NMR spectrum whereas the calculated spectrum is beset by a number of limitations. In a real life NMR, at normal temperatures, bond rotations in a molecule (where possible) occur at a rate faster than the timescale of the NMR excitation/relaxation - ergo, an average is observed for those peaks whose atoms are free to rotate (giving them an overall equal "average" environment). In a computationally generated MMR spectrum, however, this time-scale does not exist: it is a snapshot of one moment in time only. Consequently, groups which would normally be grouped together by their free rotation are seen separately (as can be seen on ultra-low temperature NMR). This means that there are far more peaks predicted than are actually visible - this makes assigning the NMR spectra particularly difficult.

In this molecule, there are few locations where free rotation is possible due to the cage-like nature of the ring structure, viz. the methyl groups. The chemical shifts produced by the atoms in these groups can be averaged to give a more life-like result and (probably) better agreement with the literature; nevertheless, in the table these values have not been averaged so as to show the full picture provided by the computational means. These methyl groups are the only examples of genuine degeneracy in the system, since they share the same chemical environment; all other protons are forced to remain as they are due to the structural nature of the molecule.

Consider atoms 12 and 13; they share a carbon, yet atom 12 has a lower chemical shift (i.e. it is more shielded). A similar situation is noticeable throughout the molecule - the protons on the same face as the downwards-pointing carbonyl have lower chemical shift values. Is this perhaps evidence of through-space interactions? Direct NMR interactions are well known, but the limits of through-space interactions are not fully understood. An atom bearing lone pairs like oxygen will be able to affect the NMR situation of neighbouring atoms through its electron density; while, when bonded nearby, a highly electronegative atom like oxygen will cause a deshielding effect on a proton (thus raising its chemical shift), in the case where no formal bond exists the situation may be different. The electron density is able to interact to, perhaps counterintuitively, cause a shielding effect on neighbouring (in a 3D sense, not a bonding sense) atoms. This will lower their chemical shifts and may explain why this situation exists in the molecule.

Additionally, one must always be careful when considering predicted NMR data in conjunction with literature data; the paper in question is two decades old. Given the inability to locate any alternative literature on this particular subject, it cannot be assumed that this literature data (or more aptly, their assignments of the data/multiplicities) is correct. There is a possibility that the multiplicity in the molecule may be divided up incorrectly, since the computationally predicted values do not match up well with the multiplicities suggested. Further study in this particular area is required if this question is to be answered fully.

Crystal structures of the Jacobsen and Shi catalysts

Jacobsen

The crystal structure of the Jacobsen catalyst can be located in the Cambridge Structural Database using the Conquest program; this structure can then be loaded in the accompanying program, Mercury, and this displays a pair of molecules. The Jacobsen structure is rather interesting; it is clear to see that the structure is held with the ligand mostly planar around the metal with many bulky substituents. Given that there are many bulky groups around the molecule, we can expect there to be a significant degree of interaction. It is important to note that these interactions may not necessarily be attractive - at small separations, they can add significant energy to the system, for instance through steric clash. The most stabilising interactions will occur at distances where the atoms' separation is equal to their combined van der Waals' radii (for example, H-H interactions equal to or beyond 2.4 Å will be favourable - any less than this and the energy will rise). Consider the images (the leftmost is a Jmol) below:

The Jacobsen crystal structure

Possible favourable H-interactions

Destabilising interactions

Without even visualising the crystal structure, it should be obvious from a simple drawing that this molecule will suffer from many unfavourable interactions - the nature of the tert-butyl groups are so large such that they rarely leave a molecule unaffected. There is a clear steric clash between protons on the tert-butyl groups themselves; this is expected. There is a clash (2.081 Å) between protons from t-butyl groups on opposite sides of the molecule (on the empty face) - this can be expected to be destabilising. A more energetically unfavourable situation exists with the phenyl groups - the planar arrangement forced upon them causes the tert-butyl to be meta to each other. This is not a problem in itself, a problem exists for the proton stuck between the groups (in the ortho position to the groups). This proton is well within steric clash distance (1.681 Å) - this can be expected to be highly unfavourable.

These are the interactions of key significance within the molecules, and while other interactions may be present within the molecule, they will not be as significant.

Shi

The same procedure as followed for the Jacobsen crystal structure can be used to elucidate the Shi catalyst structure. This is displayed below. In this instance, steric effects are not particularly important - rather the distances of C-O anomeric bonds can be measured. In this molecule are present two key structures of interest, the six-membered oxygen-containing ring (much like a sugar) and the 5-membered acetal ring. Two molecules of the catalyst are provided when the structure is loaded in Mercury, and differences in the lengths were noticed. For this reason, both molecules' data are included. Bond data are provided below. The bond distances in the table are labelled on the jmol and can be examined at leisure.

C-O bond distances (Angstroms) C-O bond Distance (Mol. I) Distance (Mol II) Acetal I 1.44 1.46 Acetal II 1.43 1.43 Sugar I 1.42 1.42 Sugar II 1.41 1.42

The Shi crystal structure

Analysis of the structures and bond length reveals some interesting effects and confirms some theoretical predictions of conformational analysis. The oxygen atom attached to the six-membered ring anomeric centre is in the axial position (known as the α-anomer) - this is the more stable anomer in the large majority of cases involving -OR attached at the anomeric centre (the β-anomer can be stabilised by hydrogen bonding when -OH is attached - this is not the case here, and indeed this form is not seen). Given that the axial position is preferred, it is expected that some orbital overlap stereoelectronic effects will be noticed. The two C-O bonds coming out of the 6-membered ring anomeric centre are reported by Mercury (though rounded in the table above) as 1.420 Å (along the ring) and 1.405 Å (axial C-O bond) Whether these values can be trusted beyond three sig. fig. is open to debate, but for the sake of argument, it can be assumed these values are true. The greater length of the ring bond suggests a weaker bond - this deserves further consideration. It can be argued that the lone pair on the axial oxygen, O_LP is donating into the ring σ* _C-O orbital, thus weakening this bond slightly. The alignment, while not optimum, is sufficient to allow some interaction.

The same effect is visible in the 5-membered ring, except this time the effect is more severe. We can therefore conclude that the 5-membered ring is able to force the relevant orbitals into a more anti-periplanar-like alignment - we know from Conformational Analysis that this will lead to a greater interaction, hence a greater weakening of the bond.

Epoxide properties

Knowledge of the catalysts alone is interesting indeed, but what does one do with these molecules? Their primary function is in the epoxidation of alkenes - we shall examine two such epoxides produced by the catalysed reaction now. NMR spectra of the epoxides can be obtained relatively simply using a method similar to our earlier forays into NMR. Our epoxides of choice shall be styrene oxide and 1,2-dihydronaphthalene oxide; these molecules were assembled in Avogadro, given a rudimentary optimisation using the MMFF94s force field and then submitted to Gaussian with the B3LYP level of theory and the 6-31G(d,p) basis set. This not only optimises the structure further, but when set up correctly, it is able to provide predicted NMR spectra (as seen earlier). The checkpoint files in each case (.fchk) were used to evaluate the results. All calculations have been published to D-space and can be found in the references. One might ask if the other enantiomers should be considered; in this instance, it is irrelevant - the spectra will be the same, it is only the sign of the optical rotations which will change between enantiomers.

It is possible to calculate coupling constants when calculating predicted NMR spectra, but this procedure is particularly time-intensive for molecules with many atoms present within it. It is for this reason that no coupling constant calculations have been performed below, and that the literature references contain no mention of experimental coupling constants, since there is nothing to compare them to!

Styrene oxide

The proton NMR of styrene oxide

The ¹³C NMR of styrene oxide

A Jmol of the epoxide in question is provided here below, along with a summary of Carbon NMR and proton NMR data. The atom numbers given in the table can be seen on the Jmol by hovering over the appropriate atoms (or clicking on them, depending on your browser). The calculation data was published to D-space.

13C NMR data Atom no. Calculated value Literature value 5 135.1 137.6 1 & 3 123.7 128.5 2 123.0 128.2 4 & 6 120.6 125.5 7 54.0 52.3 8 53.5 51.2

(R) Styrene oxide

1H NMR data (ppm) Atom no. Calculated value Literature value 14, 12, 10, 11 7.48 7.22-7.42 (m) 13 7.30 7.22-7.42 (m) 15 3.66 3.92 (dd) 16 3.11 3.20 (dd) 17 2.53 2.87 (dd)

It is clear to see that our computational means have produced a reliable 13-Carbon NMR spectrum; a good degree of similarity with the literature, with some small differences. The values for atoms 4 & 6 and 1 & 3 have been averaged - this is again due to the way in which the predicted NMR spectrum is calculated. Since the predicted spectrum is an instant "snapshot" of a system, with no regards for typical NMR timescales, these atoms have different peaks; these different peaks in an experimentally determined spectrum would coalesce due to the free rotation of the aryl-substituent bond. It is for this reason that the values for these atoms have been averaged in the table.

A similar situation exists in for the proton NMR, and the agreement with literature is good. Consider the table, the computed value for Atom 13 is slightly lower than those for the other aryl protons (10, 11, 12 and 14). This is again due to the fact that the computational method takes a spectrum at one precise instant in time, not allowing for rotation; in this instance, the epoxide-bearing substituent is able to rotate around the aryl-substituent bond in real time, giving the literature values provided. In the computational case, the epoxide group (bearing its electronegative oxygen atom) is certainly pointing in a specific direction (in the direction of the hydrogen labelled atom 13); there will be a degree of through-space interaction present which will affect the chemical shift of this proton, and indeed this is shown in the calculated data. This is not noticed when determined by experiment.

It is important to note that both of these cases involve the limitations of quick NMR calculations by computational means; this does not mean the spectra are invalid. Indeed, if an experimentally determined NMR were run at a sufficiently low temperature, the spectra could begin to resemble the computationally predicted ones as bond rotation becomes less facile. An alternative exists whereby we can calculate NMR snapshots over a time period, which would yield more realistic NMR spectra, though naturally at the cost of vastly increased number-crunching time.

1,2-dihydronaphthalene oxide

The proton NMR of 1,2-dihydronaphthalene oxide

The ¹³C NMR of 1,2-dihydronaphthalene oxide

We can perform a similar exercise for this molecule. Again the atom numbers are visible in the Jmol - the calculation data for this molecule can be found on D-space.

13C NMR data (ppm) Atom no. Calculated value Literature value 3 133.1 136.7 4 130.9 132.5 5 127.7 129.5 1 124.2 128.4 2 123.5 128.4 6 120.0 126.1 8 47.5 55.1 7 44.6 52.7 16 18.0 24.4 19 11.8 21.8

1,2-dihydronaphthalene oxide

1H NMR data Atom no. Calculated value Literature value 11 7.59 7.39 (d) 9 7.41 7.26 (dd) 12 7.30 7.20 (dd) 10 7.24 7.09 (d) 14 3.29 3.74-3.73 (m) 17 3.08 2.79 (ddd) 18 2.96 2.55 (dd) 21 & 13 2.69 2.44-2.39 (m) 20 2.25 1.77 (ddd)

The ¹³C predicted spectrum bears reasonably good agreement with the literature; though there is some disparity (roughly 4 ppm in some cases), this is likely due to the aromatic system present in naphthalene oxide combined with the effects of the oxygen. The differences between the carbons on the ring system, however, expected - such differences occur in the literature too. There is no rotation as the epoxide is locked onto the ring-structure, so each position is affected to a different degree, hence the slight differences. The two vastly different peaks (atoms 9 & 10) are caused by the fact that they are the immediate neighbours to the epoxide oxygen. Oxygen, bearing its lone pairs, is a source of much electron density - this density shields the nuclei moving them upfield (to a lower chemical shift). Additionally, the two sp³ carbon atoms (Nos. 16 & 19) have considerably lower chemical shifts than the rest of the molecule; this is probably due to their bonding situation (both being bonded to two hydrogens) but also there may be an element of through-space interaction with the oxygen atom. The distance between them is not too great to discount these effects, but further study is required to achieve greater understanding.

For the ¹H NMR, however, our agreement between calculated values and literature is not so good - the figures for some peaks are similar, but some are considerably different. It is quite possible that this is a result of complex effects of the aromaticity combined with various through space interactions with the oxygen. Further study must be undertaken if we wish to elucidate fully what is happening here - the current method provides a very rough data set, so a superior level of theory/basis set must be used for more accurate results.

A comparison of the optical rotations

It is perhaps the first property of enantiomers that a chemistry student will learn, that they rotate plane-polarised light in a specific direction. Consequently, we can thus determine which enantiomeric configuration is present by measuring the optical rotation of experimentally obtained molecules - this is of key importance in asymmetric synthesis. It is also equally possible to predict these values computationally, and this is what is performed here.

Using the previously optimised molecules (q.v. the previous NMR section), a new calculation can be set up to predict the optical rotations. The calculation is run with precisely the same level of theory and basis set (B3LYP/6-31G(d,p)) as before; were this not the case, the results would be essentially meaningless - they may well be correct, we would merely have no way of discerning this. It is always important to keep the same basis sets when calculating further properties of a molecule after an optimisation. The optical rotations were calculated at 365 nm and 589 nm - these values were not picked at random, rather they are the wavelengths emitted by a mercury-vapour lamp (365.4 nm I-line) and a sodium-vapour lamp (589.3 nm average). All of these calculations were also performed in the same solvent system as above, namely chloroform. The calculations undertaken for this section were published to D-space.

Optical rotation (degrees) Molecule 589 nm 365 nm 1,2-dihydronaphthalene oxide -46.78 -96.66 (R)-Styrene oxide -30.15 -94.16

Before continuing with the analysis of the optical rotations, it is important to note that values calculated to be less than 100° can be unreliable, so this must be considered at all times. The data yielded for (1S,2R)-dihydronaphthalene oxide bear reasonable agreement with literature (-39° at 589nm in chloroform). There is considerable difference between literature values using the same apparent conditions - for this reason, the predicted value's accuracy is to be viewed carefully in absence of a definitively correct literature value. No literature was found for the value at 365 nm.

The values for (R)-Styrene oxide bear reasonable agreement with the literature, notwithstanding some slight deviations. Indeed the literature is not at all clear, various papers suggest figures anywhere from -19° to above -40°; this is due to the varying conditions when measuring the optical rotations. Solvent, temperature and concentration can all affect this result to a significant degree. This is one of the key reasons why computational calculation of optical rotation is very important - it provides another reference point in an effort to obtain true values. Again no literature value was found for 365 nm.

The transition state of trans-β-methyl styrene

The required optimised transition structure for this section was provided, since the calculation to find said state takes a significant amount of time. Data are available for both reaction schemes, and consequently both will be probed in this section.

Calculation of the enantiomeric excess

Since the free energies of the transition states are known, it is thus possible to determine the enantiomeric excess the reaction provides. This can be done meticulously and more accurately by calculating the contributions from all eight transition states, but would be overly costly in terms of time. Rather, a simplified approach is used in which one can assume that the only reaction pathways occurring do so via the lowest energy transition states, namely the (R,R) and (S,S) structures (determined by examining all the available files on the Wiki). It is straightforward to locate the free energies of the system, and the elucidation of the equilibrium constant is thus straightforward using the classic equation:

$△G=-RT\ln K$

This can easily be solved for K, and we also know that we can express K as the ratio of the mole fractions (F_SS & F_RR) of the substances. This, when rearranged (and remembering that mole fractions must sum to 1), yields a pair of equations which can be solved like so:

$F_{SS}=\frac{K}{K+1}$ $F_{RR}=\frac{1}{K+1}$

From here it is clear to see that the end result, the equation for enantiomeric excess, can be expressed thus:

$ee=\left|\frac{1-K}{K+1}\right|$

Jacobsen epoxidation

Using the formula obtained above, we can now sub in our values for the energies from the available transition states. The files provided are used as the means of obtaining the transition state data, but the values used for energies can be obtained in the .log files; they are found under "Sum of electronic and thermal free energies". The lowest energy (R,R) state has a value of -3383.253816 a.u. while the lowest (S,S) has a value of -3383.262481, giving a difference of 0.008665 a.u. (Note: care must be taken to ensure this value is converted into Joules when calculating the equilibrium constant). The equilibrium constant has a value of 9724 - this is rather high. This value indicates that the (S,S) enantiomer is considerably more prevalent; whether this is genuine or merely a result of some overly optimistic computations remains to be seen. The enantiomeric excess is thus:

$ee=\left|\frac{1-9724}{9724+1}\right|=0.9998=99.98\mathrm{\%}$

Is this value too good to be true? Alas quite probably: in the literature, it is stated that this reaction proceeds with maximum enantiomeric excesses of 92% (measured by GC) This paper is concerned primarily with cis-alkenes, and indeed the catalyst is generally used for the epoxidation of cis-alkenes - this may explain why our figure is a little off the mark.

Shi epoxidation

Precisely the same procedure can be undertaken to determine the enantiomeric excess of the Shi catalyst on trans-β-methyl styrene, and is performed below. The transition state energies in use are determined from the log files of the two lowest energy states (No. 4 in both lists).

$E(R,R)=-1343.032443a.u.$$E(S,S)=-1343.024742a.u.$ $△G=20.218977kJ/mol$

This yields a value of K = 0.0002845. This we can then sub in to the full equation for enantiomeric excess:

$ee=\left|\frac{1-0.0002845}{0.0002845+1}\right|=0.99943$

This is a rather high value; literature provides a value of 95.5% enantiomeric excess for trans-methyl styrene. Though this value is high, it must be remembered that literature values reported will depend on solvents and conditions used and therefore may differ from expected results produced through computational means, explaining why they are not as high. Despite this, such a high value does confirm the value of the Shi catalyst in asymmetric synthesis of epoxides - a very useful tool.

Non covalent interactions (NCI) analysis

What is the cause of the enantiomeric excess in this reaction? We have available to us a means of attempting to answer this question: non-covalent interaction analyis. These interactions include van der Waals' interactions, steric effects, hydrogen bonding etc, but as the name implies, do not include covalent bonds themselves. The surfaces produced by this method are made by computing electron densities around the molecules and determining where likely favourable or unfavourable interactions will occur. Let us examine the surface produced for the lowest transition state of the Shi epoxidation of trans-methyl styrene, given here below as a Jmol.

Orbital

Colour coding Colour Interaction Blue Very attractive Green Somewhat attractive Yellow Somewhat repulsive Red Very repulsive

Perhaps the most notable feature on the surface is the presence of the "doughnut" ring between the alkene and the oxygen atom soon to be an epoxide - its curious shape and mixture of favourable/unfavourable interactions suggests that many processes are occurring at this time and location. Let us consider this region in more detail. We can determine that this region is where a new bond will be forming, as there are clear signs of a mixture of non-covalent interactions (the ring) and covalent interactions (the hole in the ring). This region could be further defined at the cost of greater computing time, but for our present purposes we shall leave it be.

The green region between atoms A' and A" (labelled on the Jmol) shows a region of favourable non-covalent interactions. Since we know they cannot be bonds (else they would not be included), it is reasonable to suggest that these regions are due to a favourable van der Waals' interaction between atoms on the two molecules; in other words, the distances between interacting atoms are greater than their summed Van der Waals' radii - the interaction is favourable.

Conversely, let us consider the region between the oxygen atoms labelled B and C - there appears a patch of red surface, which shows a high degree of unfavourable interaction. This can be accounted for by either steric effects from the 5-membered ring forcing the atoms closer together, or alternatively by the high electron density on the oxygen atoms. Two atoms with high electron density on them close together in the ring will cause significant electronic repulsive effects, which will not be covalent in nature - consequently they appear on the NCI-surface. Now let us consider the case on the other side of oxygen C, between it and the proton on the 6-membered "sugar-like" ring. There is a region of mixed green and yellow interaction, indicating the presence of of both attractive and repulsive interactions (and it appears that there is more attraction than repulsion present. This is most likely a fine example of hydrogen bonding, and since it is not a covalent interaction we can rest assured that it will show up if present. We would likely expect a hydrogen close in 3D to an oxygen atom to experience a degree of attraction to the oxygen - this indeed appears to be the case.

QTAIM analysis

The QTAIM picture of trans-methyl styrene

We can also subject this transition state to an analysis through the Quantum Theory of Atoms In Molecules (QTAIM), which also measures the electron density; instead of plotting surfaces and favourable interactions outside of bonds, however, QTAIM provides data on the presence of Bond Critical Points. If we consider the shape of the potential energy surface of a bond, the nuclei involved will sit at minima on it. Correspondingly, the BCP will occupy a position on the "hill", or saddle point: these can be visualised using a QTAIM analysis in Avogadro2. The resulting diagram (atoms are purple, BCPs are yellow) is shown in the thumbnail.

One can easily see that the QTAIM analysis has revealed some interesting effects; a fine example of these is provided at position A (labelled in the picture). We can see a web of interactions between catalyst and alkene transition structure - it is these interactions which hold the structure in place and ensure the selectivity of the overall reaction. A separate interaction of interest can be seen at B - this region of the molecule is not the active site, so why should this be happening here? To elucidate the cause behind this would take a much more rigorous computational procedure (for which, sadly, no time was available) and a full examination of the molecular orbital situation. This interaction may serve to stabilise the overall molecule, or alternatively it may be irrelevant. Further examination in this particular area is required to obtain a greater understanding.

Consider the picture of the anomeric carbon - the bonds either side of it are visibly asymmetric. We can presume that this is the result of the different molecular orbitals used to construct these bonds; since different molecular orbitals have different energies, coefficients and spreads of electron density, it is fair to assume that this is the cause of the different bond lengths in this instance.

Remarks

Both NCI and QTAIM analyses of molecules provide much interesting data, but it is perhaps NCI analysis which is the more important. Such an analysis can produce an image (as above) which instantly shows the extent of interactions in a molecule outside of a bond - particular steric clashes, favourable interactions (H-bonding) and so on can all be seen in a very intuitive way for very little cost. Overall, it is a very useful technique.

Further study

To finish up this experiment, we shall peruse the literature in search of more alkenes with optical rotations between -500° and 500°. This task is multifaceted; we can discover alkenes suitable for future study by younger cohorts of students, or we can can discover those with particularly interesting properties. Given what we know (or indeed don't know) from literature about optical rotations, examining more alkenes computationally would be a useful exercise. The considerable range found in literature values for rotations does the budding chemist a disservice - which value is he to trust? Predicting these values computationally can go some way towards answering this question.

A Reaxys search using the epoxide sub-structure and an optical rotation less than 500° was carried out, and from that search the following alkene was chosen. The intention originally was to use 2,2-dimethyl-2H-1-benzopyran, but this was not found to be available from Sigma-Aldrich. Instead, 2,2-Dimethyl-2H-1-benzopyran-6-carbonitrile was located instead, pictured below.

This structure was chosen due to its similarity to an alkene we have ourselves examined, namely 1,2-dihydronaphthalene, and it is this similarity which would be probed - it is quite possible that the situation, particularly with the molecular orbitals, would be dissimilar to the naphthalene. It would be an interesting exercise to compare the predicted data yielded by this new compound with the data we have gleaned for the naphthalene. Within the realms of optical rotations in particular, literature data is available (and more importantly, literature data in multiple solvents!):

Optical rotation from literature(degrees)

Solvent	589 nm
CHCl3	0.62
THF	31

The optical rotations can be predicted, and indeed in different solvents. This allows for a rough determination of the accuracy of a predicted result by comparing with the literature values. In terms of the absolute configuration of the epoxide produced by the catalysts acting on the starting alkene, this can be calculated by measuring the optical rotation; both enantiomers are reported.

In addition to optical rotations, a wealth of NMR data is available (for example one 300MHz proton NMR), allowing an in depth comparison and discussion of the results. An IR spectrum is also available, should frequency analysis and IR prediction wish to be undertaken.

Starting with this molecule, it would be possible to measure the effects of moving the oxygen atom to different locations around the rings, running calculations on these different isomers and then comparing them - it is the author's opinion that the molecular orbital situation in these molecules would be particularly interest due to the presence of the unsettling oxygen atom. The NMR data would be of great use in comparison, as moving the oxygen around would change the degree of shielding/deshielding experienced by other atoms and consequently change chemical shifts.