Rep:Mod:PA2612

Bonding and Molecular Orbitals in Main Group chemistry

EX₃ Section

In running an optimization, we are trying to determine the minimum energy configuration of a molecule. This is found when the molecule is in the equilibrium position, that is when there are no forces acting on the molecule eg. nuclear-nuclear repulsion, electron-electron repulsion and electron-nuclear attraction. The configuration is such that repulsions are minimized and attractions optimized.

In order to carry out these optimizations, the Born Oppenheimer approximation is applied; this states that due to the much larger size and mass of the nuclei in comparison to electrons, they are stationary. The Schrodinger equation is then solved for the electrons. The result of this is an energy that is dependent on the position of the nuclei. Because of this, moving the nuclei will result in a change in the energy due to changes in the electrostatic interactions.

In the course of the optimization, the nuclei are moved slightly and the energy calculated. Comparing these energies allows for the nuclei to be shifted in the optimum direction (that with the lower energy) until the lowest energy structure is identified.

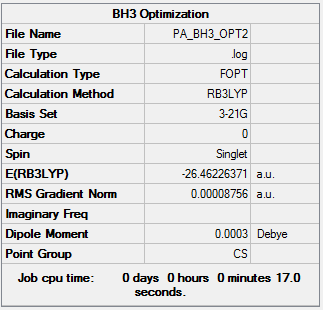
BH₃:B3LYP/3-21G Optimization

A BH₃ optimisation was run using the 3-21G basis set and B3LYP method. We set the position of the nuclei and the B-H bond distances were changed to 1.53 Å, 1.54 Å and 1.55 Å in order to break the symmetry of the molecule.

The results form this optimisation are summarized below:

Optimisation log file here

summary data

convergence

Jmol

         Item               Value     Threshold  Converged?
 Maximum Force            0.000217     0.000450     YES
 RMS     Force            0.000105     0.000300     YES
 Maximum Displacement     0.000692     0.001800     YES
 RMS     Displacement     0.000441     0.001200     YES

Optimized BH3

From this summary it can be seen that the expected D_3h is not achieved. This is due to the fact that very accurate numbers are needed in order to obtain the correct symmetry. This is not achieved form building the molecule in the way that was done so here. In addition, the symmetry was broken by changing the B-H bond lengths.

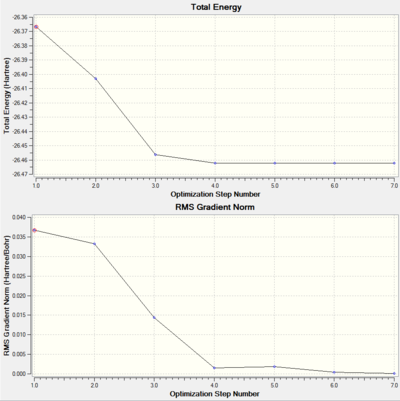
We were also able to generate graphs showing how the energy changes with each step of the optimization and the the gradient of the energy of the molecule at each step if the optimization, with the last step having the lowest energy and smallest gradient.

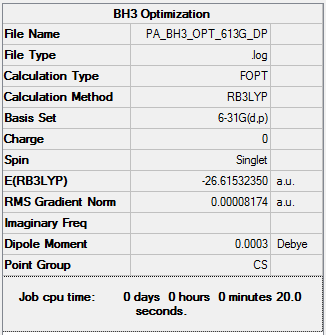
BH₃:B3LYP/6-31G(d,p)

A further BH₃ optimisation was run. This time using a higher basis set, 6-31G. The basis set is used to determine the number of functions used to describe the molecules. The more functions used the more accurate the description. Functions that allow for specific things such as electron density being able to expend out and away from the molecule and polarization functions enable us to obtain a very accurate description.

Optimisation log file here

summary data

convergence

Jmol

         Item               Value     Threshold  Converged?
 Maximum Force            0.000203     0.000450     YES
 RMS     Force            0.000098     0.000300     YES
 Maximum Displacement     0.000867     0.001800     YES
 RMS     Displacement     0.000415     0.001200     YES

Optimized BH

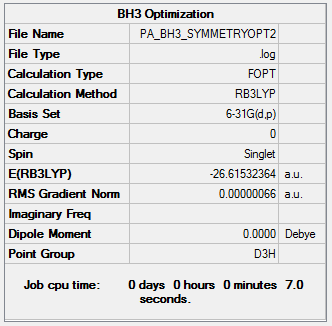
Again we would expect to observe a D_3h symmetry from this optimization but this was not achieved. A further optimization was run where the symmetry was constrained to D_3h.

Optimization log file here

summary data

convergence

Jmol

         Item               Value     Threshold  Converged?
 Maximum Force            0.000001     0.000015     YES
 RMS     Force            0.000001     0.000010     YES
 Maximum Displacement     0.000005     0.000060     YES
 RMS     Displacement     0.000003     0.000040     YES

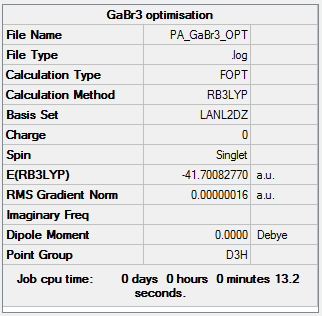
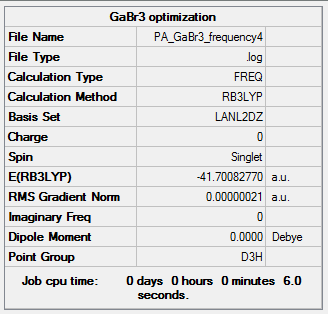
Optimized restricted symmetry BH3

GaBr₃:B3LYP/LANL2DZ

For this optimization, a pseudo potential was used. Due to the fact that Ga and Br are heavy elements with 31 and 35 electrons respectively some of the relativistic effects can not be recovered using a basis set. By using a pseudo potential we are able to recover some of these effects. A pseudo potential is based on the assumption that the valance electrons are responsible for bonding in a molecule and so the inner electrons can be modeled by the pseudo potential.

The symmetry of this molecule was restricted to D_3h.

Optimization file: DOI:10042/143672

summary data

convergence

Jmol

         Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000450     YES
 RMS     Force            0.000000     0.000300     YES
 Maximum Displacement     0.000003     0.001800     YES
 RMS     Displacement     0.000002     0.001200     YES

Optimized GaBr3

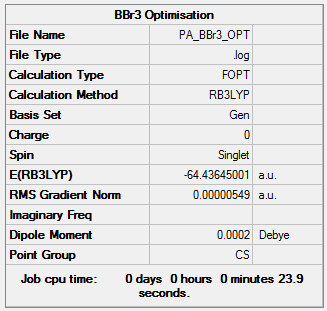
BBr₃:B3LYP/Gen

In optimizing BBr₃ pseudo potentials and basis sets were mixed. This is to accomodate for the heavy Br atoms that require a pseudo-ptential and the light Boron atoms for which calculations are more accurate with a full basis set.

Optimization file:DOI:10042/143679

Summary Data

Convergence

Jmol

         Item               Value     Threshold  Converged?
 Maximum Force            0.000011     0.000450     YES
 RMS     Force            0.000007     0.000300     YES
 Maximum Displacement     0.000047     0.001800     YES
 RMS     Displacement     0.000031     0.001200     YES

Optimized BBr3

The expected D_3h point group was not achieved. This is due to the fact that very accurate values need to be used in order to generate the correct point group.

Geometry Comparison

geometry data
	BH₃	BBr₃	GaBr₃
r(E-X)	1.19 Å	1.93 Å	2.35 Å
θ(X-E-X)	120.0°	120.0°	120.0°

In changing the substituent on the central atom, from H to Br, we see an increase in bond length form 1.19 Å to 1.93 Å. Generally, the bond length is the sum of the atomic radii of both atoms involved, as we change the ligand form hydrogen to bromine, the atomic radius is increasing and so the bond length increases. Due to the similarity in size, there is greater overlap between the boron and the hydrogen. The much larger bromine atom is unable to achieve this overlap, contributing to an increase in bond length.

Genrally the greater the difference in electronegativity if the two atoms, the shorter the bond. This is because the more electronegative atom is able to attract electrons, polarizing the bond. This means that there are now also Coulombic forces acting on the atoms, meaning the atoms are attracted more strongly and so the bond is shortened. The difference in electronegativity between boron and bromine is greater than that of boron and hydrogen. Despite this, the B-H bond is still shorter, this is because of the hydrogen is so much smaller than the bromine.

Hydrogen and bromine are only able to form single bonds (both are 1 electron short) and so bond multiplicity is not a factor in bond length. We can therefore determine that this is due to the difference in size (hydrogen has 1 electron in comparison to bromine's 35).

When we change the central atom form boron to Gallium, and keep the ligands the same (bromine) we also see an increase in bond length, from 1.93 Å to 2.35 Å. Boron and Gallium are both group 13, with 3 valence electrons. However gallium is much larger and occupies row 3 of the periodic table. Due to this increase in size, the bond length is longer. Another factor contributing to this increase is the inert pair effect. Due to the presence of filled d-orbitals, there is a greater energy difference between s and p orbitals. Therefore, the energy needed in order to promote electrons and allow for hybridization in order to generate 3 bonds is greater. The energy released on formation of new bonds is smaller and so weaker, longer bonds are formed. Again we see a bigger difference in electronegativity between gallium and bromine that boron and bromine, however it is the size of the atoms that is determining the bond length. The gallium is much larger and so the bromine-gallium bond is longer.

Changing the ligand or the central atom has no effect on bond angle, all are three molecules possess a bond angle of 120°. this is due to the fact that all three are of trigonal planar geometry and so, in order to minimize electron-electron repulsions, the atoms arrange themselves, 120° from each other.

A chemical bond exists when a region of constant potential energy contours means that the potential energy of a molecule is more favorable under atomic contraction. ^[1] Bonds are generally categorized by three main types, covalent, ionic and metallic although it is rare that bonding situations can be clearly categorized as one of these. A covalent bond arises form the 'sharing' of valence electrons in order to complete the desired octet. These electrons occupy the space in between the two atoms, attracted to the both of the oppositely charged nuclei. this overcomes any repulsive forces between the two nuclei, holding them in a fixed configuration and so a bond is formed. when an ionic bond is formed, an electron is transferred from one atom/ molecule to another in order to complete the octet. This creates charged species, one positive, one negative. The species experience electrostatic attraction resulting in a bond. Metallic bonds arise from the donation of an electron form metal atoms into a 'sea of electrons'. This results in positively charged metal atoms surrounded by delocalized electrons forming strong bonds.

An example of a strong bond is N≡N which has a bond enthalpy of 941 kJ/mol^[2] . This is a homonuclear triple bond. Due to the fact that the bond is homonuclear, the atoms, involved have the same energy and size and so there is great overlap and therefore a very strong bond is formed. An example of a medium strength bond is C-H which has a bond enthalpy of 413 kJ/mol^[2]. This is a covalent bond. Due to the similar size and energy of the molecules, there is good overlap and so a strong bond is formed. An example of a weak bond is I-I with a bond enthalpy of 152 kJ/mol^[2]. This is weak due to the large size of iodine meaning that overlap is poor.

Gaussview determines where bonds are formed form the distance between atoms. This means that, although a bond may in fact be present, the distance between the atoms is too large for gaussview to recognize this and so not bond is drawn.

Frequency Analysis

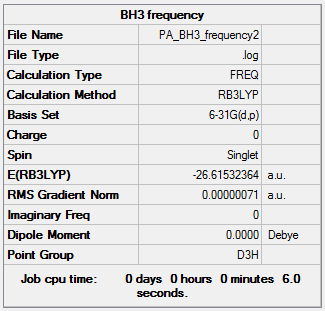
BH₃:B3LYP/6-31G9(d,p)

In order to run a frequency analysis, an optimisation of BH3 using B3LYP/6-31G9(d,p) and constrainig the symmetry to D_3h was run. This was then used to run the frequency analysis. The results of which are shown below.

Frequency file here


Summary Data	Low Modes
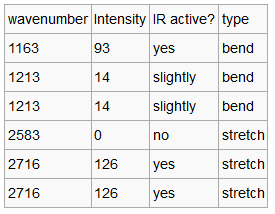
	Low frequencies --- -10.1940 -10.1821 -3.1776 0.0004 0.0579 0.4920 Low frequencies --- 1162.9850 1213.1461 1213.1463


Vibration Data	IR Spectra

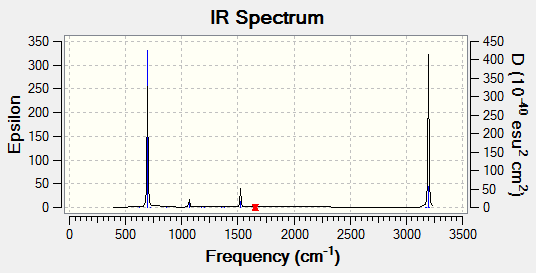
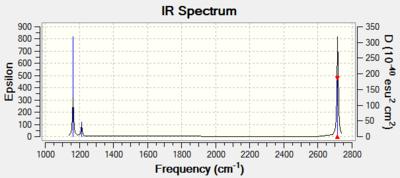
Although there are six vibrations in the BH₃ molecule (3N-6), there are only three peaks observed in the IR spectrum. This is due to the fact that there are two pairs of degenerate vibrations. These are vibrations that have the same energy and so will appear with the same wavenumber and intensity. In this molecule they are due to a bond stretch, 2716 cm^-1 and an angle deformation, 1213 cm^-1. In this case the defamation is higher in energy. One of the vibrations is not IR active, 2583 cm^-12, this a symmetric bond stretch resulting in no change of dipole and so no peak is observed.

GaBr₃:B3LYP/LANL2DZ

A frequency calculation was run on the optimized GaBr₃ molecule.

Frequency file here


Summary Data	Low Modes
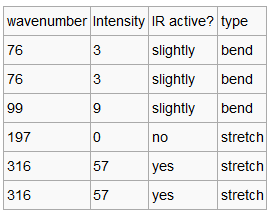
	Low frequencies --- -1.4877 -0.0015 -0.0002 0.0096 0.6540 0.6540 Low frequencies --- 76.3920 76.3924 99.6767


Vibration Data	IR Spectra

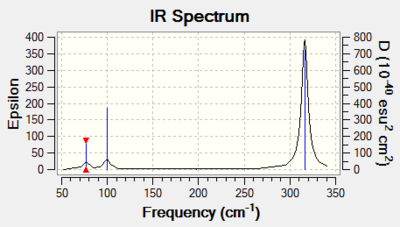
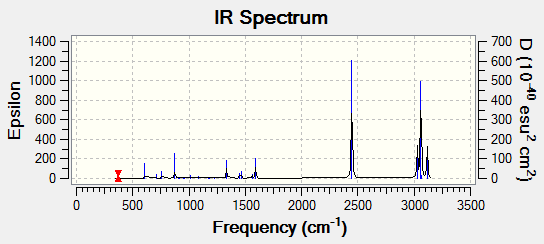
Again we can see that there are 6 vibrational modes. We can see that the symmetric stretch at 197 cm^-1, is not IR active due to the fact that there is no change in dipole. Thee are two sets of degenerate modes at 316 cm^-1 and 76 cm^-1. This means that we only observe three peaks in the IR spectrum.

Comparison

The values obtained for the frequency in the IR spectra vary greatly between the BH₃ and GaBr₃, with those in the former in the range 1163 to 2716 cm^-1 and the latter 76 to 316 cm^-1. The GaBr₃ vibrations are of higher energy. The atoms involved are heavier and so a smaller frequency is observed.

The order of the modes has also changed between the two molecules. In BH₃ the frequency due to the umbrella stretch is observed at 1163 cm^-1 where as we can see this stretch at 99 cm^-1 for GaBr₃. In the BH₃ vibration we can see that the boron atom is largely stationary and the hydrogen are moving whereas this is inverted for the GaBr₃ and we can see the central ion moving whilst the ligands remain still. This is due to the fact that in the BH₃ it is the ligands, the hydrogen, that is the lighter atom and so this moves whereas in GaBr₃ it is the gallium that is lighter and so this is the atom that moves.

For both the optimization and the frequency the basis set and method must be kept the same. The basis set and method use a number of approximations and the accuracy of the calculations is highly dependent on this. Comparisons can not be made between calculations using a different basis set and method as different approximations would be applied and the results rendered useless.

A frequency analysis allows for conformation that the minimum structure has been obtained. The data obtained can be used to determine the thermo-chemistry of the molecule, for instance the Gibbs free energy and the enthalpy. we can also generate the IR spectra as we have done.

The low frequencies are the motions of the center of mass of the molecule. Every non-linear molecule has 3N-6 vibrational modes, the frequencies listed are the '-6'. The first three values obtained are translational, the second three rotational and the values on the second line are the vibrations. The closer the rotational and translational value are to zero the better the results.

BH₃ B3LYP/6-31G9(d,p) MO

In order to determine the molecular orbitals of BH₃, an energy calculation was run using B3LYP/6-31G9(d,p). The energy of the first 8 molecular orbitals was given and the orbitals visualized in order to create a molecular orbital diagram.

DOI:10042/144126

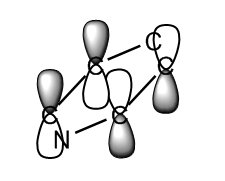
LCAO theory was used to predict the MOs. These can be seen next to the real MOs. The 1a'₁ orbital the non-bonding 1s orbital of boron. This is considerably lower in energy and is therefore not involved in mixing. This is reflected in the real MO. For the 2a'₁ MO, the LCAO MO shows a strongly bonding orbital due to through bond and through space bonding interactions. This is also reflected in the real MO. We can see that there is only one phase present and this covers the whole molecule showing us the it is a bonding MO. There are two degenerate 1e' molecular orbitals. They are bonding orbitals although the interaction is not as strong as the 2a'₁ MO, which is evident from it being higher in energy. We see through bond bonding interactions but through space anti-bonding interactions. This is reflected by the change in phase that we can see in both the LCAO and real MO. The 1a"₂ is the non bonding p_z orbital. There is no other orbital with the same symmetry for this to mix with. This can be seen form the real orbital also. The 3a'₁ is a non bonding orbital seen by the out of phase overlap. The s-s interactions are strong and so this orbital is destabilized a considerable amount despite the though space bonding interactions. The LCAO description of this orbital is in great agreement with the real MO. The degenerate 2e' orbitals are also anti-bonding. Although the s-p orbital overlap isn't as good as s-s, there is through bond and through space anti-bonding interactions, seen by the changes in phase, meaning these orbitals are of high energy. The LCAO and real MOs are in good agreement.

For BH₃ qualitative MO theory accurately predicts the molecular orbitals, however it can leave some questions about the order of these orbitals. It is difficult to tell whether the 2e' or the 3a'₁ orbitals are higher in energy. This is due to the fact that the s-s interactions in 3a'₁ are stronger than the s-p in 2e' suggesting that this would be more anti-bonding and so higher in energy. However the a'₁ energy levels are lower than the e', meaning that the 3a'₁ could be lower in energy. From the calculations carried out we are able to determine the energies of these orbitals and can see that the 2e' is in fact higher in energy. Are there any significant differences between the real and LCAO MOs? What does this say about the accuracy and usefulness of qualitative MO theory?

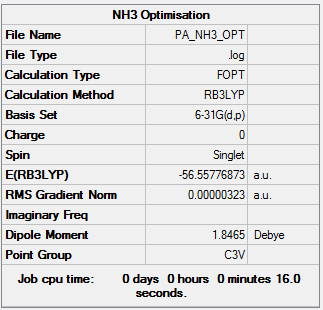
NH₃:B3LYP/6-31G(d,p)

Optimisation

The 613-G(d,p) basis set was used in order to optimize the NH₃ molecule.

Optimisation log file here

summary data

convergence

Jmol

       Item               Value     Threshold  Converged?
 Maximum Force            0.000006     0.000450     YES
 RMS     Force            0.000004     0.000300     YES
 Maximum Displacement     0.000012     0.001800     YES
 RMS     Displacement     0.000008     0.001200     YES

Optimized NH3

we can see that a point group of C_3v was achieved. An angle of 105.7 and bond length of 1.02 Å was found.

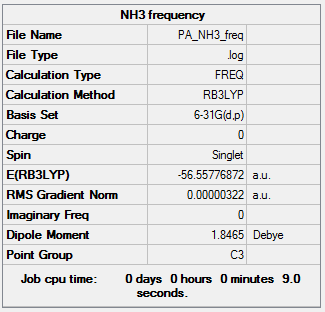
Frequency Analysis

Frequency file here


Summary Data	Low Modes
	Low frequencies --- -0.0138 -0.0026 -0.0009 7.0783 8.0932 8.0937 Low frequencies --- 1089.3840 1693.9368 1693.9368


Vibration Data	IR Spectra

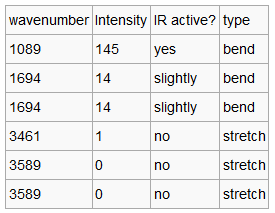
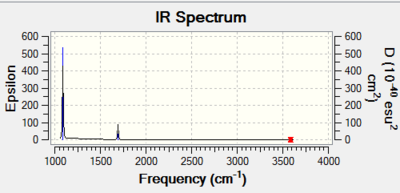
We can see that there are 6 vibrational modes in this molecule (3N-6). However only two are seen in the IR spectrum. This is sue to the fact that there are two degenerate peaks at 1694 am^-1 and so only one peak is observed, with an intensitry of 14. The other peak we can see is at 1089 am^-1. both of these peaks are due to angle deformation in the molecule. The other peaks, sue to stretches, so not result in a change in dipole and so are not IR active.

Population Analysis

Population file here

NBO analysis

NBO analysis here

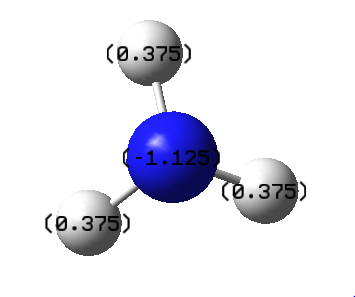
The charge distribution of the NH₃ molecule is shown below. Bright green represents highly positive charge and bright red highly negative charge. The nitrogen atom is much more electronegative and so, as expected, is coloured red and the hydrogen atoms green.

The charge range, -1.25 to +1.25 can be seen below.

The specific NBO charges for the nitrogen and hydrogen can be seen below.

From the summary of natural population analysis we can see that 69% nitrogen-hydorgen bonds are contributed to by the nitrogen orbitals. These have a hybridiatsion of 25%s+75%p. the other 31% of the bond is contributed by the hydrogen orbital which is 100% s. We can say that the nitrogen has formed 4 sp³ orbitals whcih interacts with a s atomic orbital of hydrogen.orbitals 1., 2., 3..

From this analysis we can also see the core 1s atomic orbital of nitrogen (4.) Orbital 5. is the 4th sp³ orbital occupied by the lone pair of nitrogen.

 1. (1.99909) BD ( 1) N   1 - H   2  
               ( 68.83%)   0.8297* N   1 s( 24.86%)p 3.02( 75.05%)d 0.00(  0.09%)
                                           0.0001  0.4986  0.0059  0.0000  0.0000
                                           0.0000  0.8155  0.0277 -0.2910  0.0052
                                           0.0000  0.0000 -0.0281 -0.0087  0.0014
               ( 31.17%)   0.5583* H   2 s( 99.91%)p 0.00(  0.09%)
                                           0.9996  0.0000  0.0000 -0.0289  0.0072
    2. (1.99909) BD ( 1) N   1 - H   3  
               ( 68.83%)   0.8297* N   1 s( 24.86%)p 3.02( 75.05%)d 0.00(  0.09%)
                                           0.0001  0.4986  0.0059  0.0000 -0.7062
                                          -0.0239 -0.4077 -0.0138 -0.2910  0.0052
                                           0.0076  0.0243  0.0140  0.0044  0.0014
               ( 31.17%)   0.5583* H   3 s( 99.91%)p 0.00(  0.09%)
                                           0.9996  0.0000  0.0250  0.0145  0.0072
    3. (1.99909) BD ( 1) N   1 - H   4  
               ( 68.83%)   0.8297* N   1 s( 24.86%)p 3.02( 75.05%)d 0.00(  0.09%)
                                           0.0001  0.4986  0.0059  0.0000  0.7062
                                           0.0239 -0.4077 -0.0138 -0.2910  0.0052
                                          -0.0076 -0.0243  0.0140  0.0044  0.0014
               ( 31.17%)   0.5583* H   4 s( 99.91%)p 0.00(  0.09%)
                                           0.9996  0.0000 -0.0250  0.0145  0.0072
    4. (1.99982) CR ( 1) N   1           s(100.00%)
                                           1.0000 -0.0002  0.0000  0.0000  0.0000
                                           0.0000  0.0000  0.0000  0.0000  0.0000
                                           0.0000  0.0000  0.0000  0.0000  0.0000
    5. (1.99721) LP ( 1) N   1           s( 25.38%)p 2.94( 74.52%)d 0.00(  0.10%)
                                           0.0001  0.5036 -0.0120  0.0000  0.0000
                                           0.0000  0.0000  0.0000  0.8618 -0.0505

From the Natural Bond Orbitals Summary, we can see that the N-H bonds all have the same energy, whilst the energy of the lone pair is higher. The core orbital is considerably lower which is why it is not involved in bonding.

NBO                        Occupancy    Energy   (geminal,vicinal,remote)
====================================================================================
Molecular unit  1  (H3N)
    1. BD (   1) N   1 - H   2          1.99909    -0.60417   
    2. BD (   1) N   1 - H   3          1.99909    -0.60417   
    3. BD (   1) N   1 - H   4          1.99909    -0.60417   
    4. CR (   1) N   1                  1.99982   -14.16768   
    5. LP (   1) N   1                  1.99721    -0.31757

The fact that the fourth sp³ hybrid orbital is occupied by te lone pair of the nitrogen can be used to explain the bond angles achieved in the optimized geometry, 105.7°. This differs form the expected geometry of a sp³ hybridised molecule by ~2°. This is due to the fact that the sp³ orbital containing the lone pair has a higher occupancy and so repels the other, bonging orbitals more.

NH₃BH₃: B3LYP/6-31G(d,p)

The molecule NH₃BH₃ was studied in order to determine the bond energy between nitrogen and boron. This is a dative covalent bond; the nitrogen has a lone pair of electrons whcih it donates to the electron deficient boron atom. The NH₃ is a Lewis acid and the BH₃ is a Lewis base.

Optimization

An optimization was run on the amonia borane using B3LYP/6-31G(d,p).

Optimization file here

summary data

convergence

Jmol


          Item               Value     Threshold  Converged?
 Maximum Force            0.000002     0.000015     YES
 RMS     Force            0.000001     0.000010     YES
 Maximum Displacement     0.000023     0.000060     YES
 RMS     Displacement     0.000010     0.000040     YES
 Predicted change in Energy=-8.534243D-11

Optimized NH3BH3

Frequency

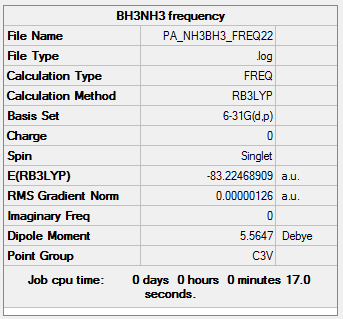
A frequency calculation was also run on the optimized molecule.

Frequency file here


Summary Data	Low Modes
	Low frequencies --- -5.5864 -0.3045 -0.0443 0.0012 1.2181 1.2915 Low frequencies --- 263.2842 632.9623 638.4603


Vibration Data	IR Spectra

Bond Energy

The dissociation energy of the N-B bond was determined using the total energies recorded form the optimization of the molecules NH₃, BH₃, the reactants, and BH₃NH₃. the product.

E(BH3)=-26.6153235 AU

E(NH3)=-56.5577687 AU

E(NH3BH3)=-83.2246891 AU

ΔE=E(NH3BH3)-[E(NH3)+E(BH3)] =-0.0515969 AU =-135.45 kJ/mol^-1

This shows that the N-B bond is relatively weak. The energy needed to break it is small.

Project: Aromaticity

In this project the conformers, vibrations and MOs of benzene and it's analogues, boratabenzene, pyridinium and borazine were studies and compared in order to see the effects of exchanging benzene's C-H fragments with isoelectronic main group fragments.

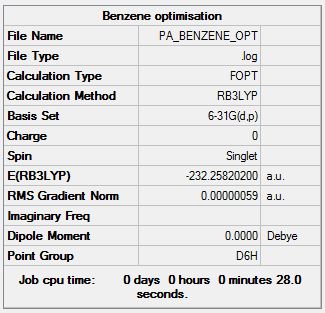
Benzene B3LYP/6-31g(d,p)

Optimization

An optimization of benzene was run using the 6-31G9d,p) basis set, the results of which are shown below.

Optimization file here

summary data

convergence

Jmol


          Item               Value     Threshold  Converged?
 Maximum Force            0.000002     0.000015     YES
 RMS     Force            0.000001     0.000010     YES
 Maximum Displacement     0.000023     0.000060     YES
 RMS     Displacement     0.000010     0.000040     YES
 Predicted change in Energy=-8.534243D-11

Optimized Benzene

We can see that the molecule is highly symmetrical with D_6h point group. The carbon carbon bond lengths are 1.40 Å. This lies in between the average length for a single and double carbon carbon bond, 1.54 Å and 1.34 Å respectively. This suggests delocalization of the pi bonds.

Frequency

A frequency analysis was then run on the optimized benzene molecule.

Frequency file here


Summary Data	Low Modes
	Low frequencies --- -10.2548 -5.6645 -5.6645 -0.0056 -0.0056 -0.0008 Low frequencies --- 414.5451 414.5451 621.0429

From the data obtained, we can see that there are 30 vibrational modes (3N-6). However due to the highly symmetrical nature of benzene, many of these vibrations do not cause a change in dipole and so are not IR active. Only 7 of the vibrational modes are IR active however there are three sets of degenerate modes and so only 4 peaks are observed on the IR spectrum.

Population Analysis

An energy calculation was run in order to compute the molecular orbitals of benzene.

Population file here

The results were used to construct a molecular orbital diagram for benzene. The real Mos were used to determine the LCAO MOs for the sigma and pi orbitals. The first 6 core 1s carbon orbitals were not included as they are too low in energy to be involved in mixing.

From the MO, we can see that there are a number of sigma orbitals involved in benzene. These increase in energy as the number of nodes increases, with the lowest energy MO being the fully bonding a_1g constructed of hydrogen 1s and carbon 2s orbitals. The s-s overlap is great and so the MO is stabilized greatly.

The pi orbitals, a_2u, the degenerate e_1g, the degenerate e_2u and b_2u are formed from the overlapping of p orbitals perpendicular to the plane of the ring. This overlap is poor and so the molecular orbitals are generally higher in energy.

NBO Analysis

NBO analysis here

NBO summary

From the summary of Bond orbital coefficients we can see that there are 3 types of bond present in benzene. Number 1 shows a C-C bond, this is contributed to by both atoms equally, 50%. We can see that the orbitals are made up of 35% s and 65 %p character suggesting that they are sp² hybridized. Each carbon forms two of these bonds in order to create the benzene sigma framework.

A further bond formed by each carbon is a C-H bond, number 4. The carbon contributes 62% of this bond and the remaining 38% comes form the hydrogen. The carbon orbital is made up of 30% s character and 70% p character. Although this is different to the orbitals forming the C-C sigma bonds, it contains more p character, we would still describe it as a sp² hybrid orbital. This overlaps with the hydrogen s orbital in order to form a bond.

The third type of bond found in benzene is the C=C π bond, number 3. We have already seen that the carbon atoms are sp² hybridized. This means that there is a p orbital remaining, perpendicular to the plain of the ring, containing 1 electron. This bond is made up of the overlap of these p-obitals. Again we can see that the bond is contributed to equally by each carbon, each having 100% p character.

These bonds are repeated for each carbon atom.

(Occupancy)   Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
    1. (1.98098) BD ( 1) C   1 - C   2  
               ( 50.,00%)   0.7071* C   1 s( 35.20%)p 1.84( 64.76%)d 0.00(  0.04%)
                                          -0.0001  0.5932 -0.0079  0.0006  0.7063
                                           0.0300 -0.3840  0.0193  0.0000  0.0000
                                          -0.0151  0.0000  0.0000  0.0069 -0.0109
               ( 50.00%)   0.7071* C   2 s( 35.20%)p 1.84( 64.76%)d 0.00(  0.04%)
                                          -0.0001  0.5932 -0.0079  0.0006 -0.6857
                                           0.0017  0.4197  0.0357  0.0000  0.0000
                                          -0.0135  0.0000  0.0000  0.0096 -0.0109
    2. (1.98098) BD ( 1) C   1 - C   6  
               ( 50.00%)   0.7071* C   1 s( 35.20%)p 1.84( 64.76%)d 0.00(  0.04%)
                                          -0.0001  0.5932 -0.0079  0.0006 -0.7063
                                          -0.0300 -0.3840  0.0193  0.0000  0.0000
                                           0.0151  0.0000  0.0000  0.0069 -0.0109
               ( 50.00%)   0.7071* C   6 s( 35.20%)p 1.84( 64.76%)d 0.00(  0.04%)
                                          -0.0001  0.5932 -0.0079  0.0006  0.6857
                                          -0.0017  0.4197  0.0357  0.0000  0.0000
                                           0.0135  0.0000  0.0000  0.0096 -0.0109
    3. (1.66514) BD ( 2) C   1 - C   6  
               ( 50.00%)   0.7071* C   1 s(  0.00%)p 1.00( 99.96%)d 0.00(  0.04%)
                                           0.0000  0.0000  0.0000  0.0000  0.0000
                                           0.0000  0.0000  0.0000  0.9997 -0.0133
                                           0.0000 -0.0096 -0.0170  0.0000  0.0000
               ( 50.00%)   0.7071* C   6 s(  0.00%)p 1.00( 99.96%)d 0.00(  0.04%)
                                           0.0000  0.0000  0.0000  0.0000  0.0000
                                           0.0000  0.0000  0.0000  0.9997 -0.0133
                                           0.0000  0.0195 -0.0002  0.0000  0.0000
    4. (1.98306) BD ( 1) C   1 - H   7  
               ( 62.04%)   0.7877* C   1 s( 29.57%)p 2.38( 70.39%)d 0.00(  0.04%)
                                          -0.0003  0.5437  0.0126 -0.0010  0.0000
                                           0.0000  0.8389 -0.0146  0.0000  0.0000
                                           0.0000  0.0000  0.0000 -0.0166 -0.0105
               ( 37.96%)   0.6161* H   7 s( 99.95%)p 0.00(  0.05%)
                                           0.9997  0.0014  0.0000 -

From the Natural Bond Orbitals Summary, we can see the the carbon-carbon sigma bonds are the lowest in energy at -0.68189 AU. This is expected due to the fact they are homo-nuclear and so,the orbitals are of the same energy and size and so overlap is great. This results in them being stabilized the most. The carbon-hydrogen bond has the next lowest energy at -0.51227 AU and the carbon-carbon pi bond is the highest in energy at -0.23791 AU. Again this is expected due to the fact that the p-p perpendicular overlap is poorer than the sp²-s overlap.

          NBO                        Occupancy    Energy   (geminal,vicinal,remote)
====================================================================================
Molecular unit  1  (C6H6)
    1. BD (   1) C   1 - C   2          1.98098    -0.68189  107(g),110(g),114(v),120(v)
                                                   43(v),73(v),109(g),112(g)
                                                   42(v),72(v)
    2. BD (   1) C   1 - C   6          1.98098    -0.68189  106(g),118(g),112(v),119(v)
                                                   33(v),63(v),109(g),120(g)
                                                   32(v),62(v)
    3. BD (   2) C   1 - C   6          1.66514    -0.23791  111(v),116(v),35(v),65(v)
    4. BD (   1) C   1 - H   7          1.98306    -0.51227  110(v),118(v),32(v),72(v)

Aromaticity

From the MO and NBO analysis, we can see that there is aromaticity in the ring.

The NBO analysis shows that the carbon atoms are sp² hybridized, meaning that there is a p-orbital containing one electron perpendicular to the plane of the ring. We can see that these p-orbitals form a pi bond, contributing equally. This idea is supported by the molecular orbital analysis. We can see the overlap of p-orbitals in all of the pi orbitals, a_2u, the degenerate e_1g, the degenerate e_2u and b_2u.

The bonding pi MO, the a_2u, shows that this orbital is spread above and below the ring suggesting delocalization. The higher energy pi obitals also support this theory. The optimized C-C bond length also supports the idea of delocalization.

We can see that there are 6 electrons in the pi orbitals. According to Hűckel's Rule, a system is aromatic if there are 4n+2 π electrons. Benzene obeys this rule and so we have an aromatic system.

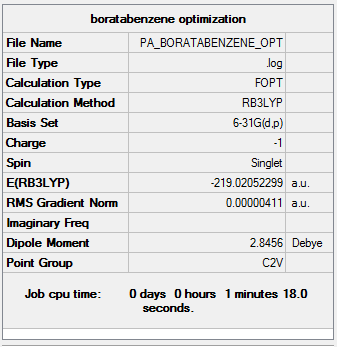
Boratabenzene B3LYP/6-31G(d,p)

A C-H group in benzene was replace by B-H. In order to keep the molecule isoelectric a negative charge was added.

Optimization

An optimization was run on the molecule using B3LYP/6-31G(d,p).

Optimization file here

summary data

convergence

Jmol

         Item               Value     Threshold  Converged?
 Maximum Force            0.000007     0.000015     YES
 RMS     Force            0.000002     0.000010     YES
 Maximum Displacement     0.000032     0.000060     YES
 RMS     Displacement     0.000009     0.000040     YES

Optimized Boratabenzene

Due to the inclusion of the B-H group in the molecule, the symmetry has been reduced and we now observe a point group of C_2v. The carbon carbon bond lengths are 1.40 Å. Again this is in between the average C-C and C=C bond length suggesting delocalization of these double bonds. The carbon- boron bonds are longer at 1.51 Å. This due to the fact there is poorer overlap between these atoms.

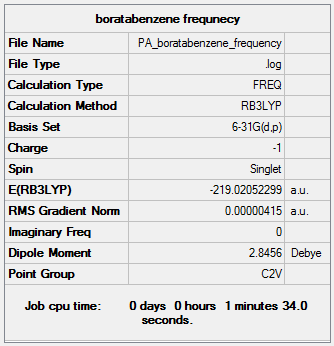
Frequency

A frequency analysis was run on the optimized boratabenzene in order to confirm that we have a minimum. The IR spectra was also generated.

Frequency file here


Summary Data	Low Modes
	Low frequencies --- -7.2570 -0.0006 -0.0006 -0.0006 3.1990 4.5294 Low frequencies --- 371.2965 404.4162 565.0822

From the IR data we can see that there are 30 modes (3N-6). However some of these are not IR active die to the fact that there is no change in dipole. Some of these are also degenerate and so not all peaks are shown on the IR spectrum. There is, however, more peaks observed than for benzene. This is due to the decrease in symmetry.

NBO Analysis

Population analysis here

NBO anaysis here

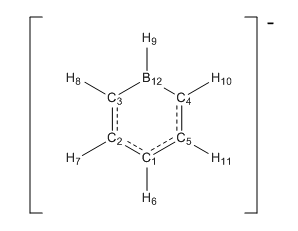
NBO Summary

From the NBO analysis we are able to look at the bonding in boratabenzene.

The boron-carbon 3, 4 bonds are made up of 66.7% carbon orbitals and 33.35 boron orbitals. This is expected due to the fact that carbon is the more electronegative atom and so is able to draw electrons away from the boron atom. The carbon orbitals have 42% s character and 58% p character where as the boron atom is sp² hybridized.

      (Occupancy)   Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
    8. (1.96998) BD ( 1) C   3 - B  12  
               ( 66.70%)   0.8167* C   3 s( 42.00%)p 1.38( 57.99%)d 0.00(  0.01%)
                                           0.0000 -0.6479 -0.0159 -0.0012  0.0000
                                           0.0000  0.6117 -0.0293  0.4525  0.0090
                                           0.0000  0.0000 -0.0059  0.0070  0.0007
               ( 33.30%)   0.5771* B  12 s( 33.40%)p 1.99( 66.52%)d 0.00(  0.08%)
                                           0.0000 -0.5779  0.0059 -0.0048  0.0000
                                           0.0000 -0.7056 -0.0393 -0.4070  0.0096
                                           0.0000  0.0000 -0.0230  0.0156  0.0005

The C₂-C₃ and C₄-C₅ bonds are composed of sp² hybrid orbitals. Despite these being homo-nuclear bonds, the contribution isn't equal, with 49% coming form the carbon adjacent to the boron (3 & 4) and the remaining 51% coming from the other carbon. This is a consequence of the electropositive boron atom.

      (Occupancy)   Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
    4. (1.98271) BD ( 1) C   2 - C   3  
               ( 50.77%)   0.7125* C   2 s( 37.60%)p 1.66( 62.37%)d 0.00(  0.03%)
                                          -0.0001  0.6131 -0.0079  0.0007  0.0000
                                           0.0000  0.0575  0.0311 -0.7869 -0.0164
                                           0.0000  0.0000 -0.0020 -0.0010  0.0179
               ( 49.23%)   0.7017* C   3 s( 32.50%)p 2.08( 67.45%)d 0.00(  0.05%)
                                           0.0000  0.5698 -0.0200  0.0010  0.0000
                                           0.0000 -0.0028  0.0270  0.8201  0.0353
                                           0.0000  0.0000  0.0006 -0.0020  0.0212

Because of the sp₂ hybridization, the carbon has a p-orbital perpendicular to the plane of the ring containing one electron. This is able to form pi-bonds. This pi bond also exhibits uneven contribution, with the larger contribution being from the carbon 3&4, 52%. This is due to the fact that the orbital involved in the C-B bond has reduced p character and so, in the pi bond, there is a larger contribution to the bond from this p orbital.

      (Occupancy)   Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
5. (1.76874) BD ( 2) C   2 - C   3  
               ( 48.12%)   0.6937* C   2 s(  0.00%)p 1.00( 99.97%)d 0.00(  0.03%)
                                           0.0000  0.0000  0.0000  0.0000  0.9996
                                          -0.0213  0.0000  0.0000  0.0000  0.0000
                                          -0.0031 -0.0171  0.0000  0.0000  0.0000
               ( 51.88%)   0.7202* C   3 s(  0.00%)p 1.00( 99.97%)d 0.00(  0.03%)
                                           0.0000  0.0000  0.0000  0.0000  0.9998
                                          -0.0054  0.0000  0.0000  0.0000  0.0000
                                          -0.0016  0.0185  0.0000  0.0000  0.0000

The remaining carbon-carbon bonds are as expected; sp² hybrid orbital contributing equally to the sigma bond and p orbital contributing equally to the pi bond.

The boron-hydrogen bond is contributed to 55.0% by the hydrogen 1s orbital. Due to the higher electronegativity of hydrogen, this orbital has the bigger contribution despite it's much smaller size. The boron contribution is in the form of a sp² hybrid orbital.

      (Occupancy)   Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
14. (1.98608) BD ( 1) H   9 - B  12  
               ( 55.09%)   0.7422* H   9 s( 99.97%)p 0.00(  0.03%)
                                           0.9998  0.0001  0.0000  0.0000  0.0180
               ( 44.91%)   0.6702* B  12 s( 33.17%)p 2.01( 66.78%)d 0.00(  0.06%)
                                          -0.0005  0.5758  0.0069 -0.0060  0.0000
                                           0.0000  0.0000  0.0000 -0.8172  0.0016
                                           0.0000  0.0000  0.0000  0.0016  0.0237

The NBO analysis is the best estimate of the bonding present. We would expect to observe a C-B pi bond in this system however this has not been shown in the NBO analysis. In an aromatic system, due to the delocalization of the double bonds, it is hard to predict where the double bonds will be. Form the MO analysis, however, we can see that the boron atom is in fact involved in the pi bonding.

The energy of the carbon-carbon sigma bond is the lowest. This is due to the fact that there is good overlap and so the orbital is stabilized most. The C-B bond is higher in energy due to the fact there is poorer overlap of these orbitals. The carbon-carbon pi bond is the highest in energy. This is due to the fact that p-p overlap is poor.

Pyridinum B3LYP/6-31G(d,p)

A N-H group replaced one of the C-H groups in benzene and a positive chrge added to the molecule to keep it isoelectric.

Optimization

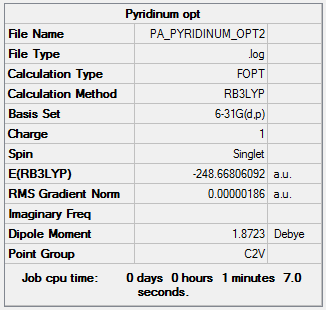
An optimization was run on the molecule using B3LYP/6-31G(d,p).

Optimization file here

summary data

convergence

Jmol


         Item               Value     Threshold  Converged?
 Maximum Force            0.000003     0.000015     YES
 RMS     Force            0.000001     0.000010     YES
 Maximum Displacement     0.000007     0.000060     YES
 RMS     Displacement     0.000002     0.000040     YES

PA_pyridinum_opt.mol

The symmetry has been reduced in comparison to benzene form D_6h to C_2v on inclusion of the nitrogen atom. The carbon carbon bond lengths are 1.39 Å between carbon 2 and 3 and carbons 4 and 5 whereas the bonds between carbon 1 and 2 and 5 and 1 are 1.40 Å. This difference is due to the electronegativity of the nitrogen atom. The bond length remains in between an average single and double bond suggesting delocalization. The carbon nitrogen bond is 1.35 Å. The C-N bond is shorter due to the fact that the nitrogen is more electronegative and so a polar covalent bond is formed. Because of the partial aromatic character, the bond is stronger and shorter than that of a single C-N bond.

The carbon hydrogen bond is longer than the nitrogen hydrogen bond, 1.08 Å in comparison to 1.01 Å. Again this is due to the electronegative nature of the nitrogen.

Frequency

A frequency calculation was run on the optimized molecule and an IR generated from the results.

Frequency file here


Summary Data	Low Modes
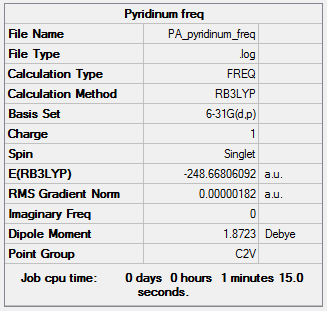
	Low frequencies --- -9.3869 -2.9694 -0.0005 0.0005 0.0010 0.9012 Low frequencies --- 391.9008 404.3425 620.1996

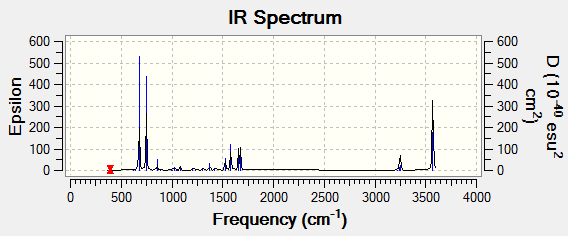
There are 30 vibration modes in pryridinium. However these don't all show in the IR. The mode is not IR active when there is no change in dipole and so no peak is seen. there are also several sets of degenerate peaks in the spectrum.

NBO Analysis

Population file here

NBO analysis file here

The nitrogen-carbon 3,5 bond is contributed to 36.3% by the nitrogen orbital. This is due to the fact that it is more electronegative and so is able to attract the carbons electrons. This orbital is has 36.5% s character and 71.7% p character. The carbon orbital is made up of 28.1% s character and 71.7% p character.

 9. (1.98862) BD ( 1) C   3 - N  12  
               ( 36.68%)   0.6057* C   3 s( 28.13%)p 2.55( 71.74%)d 0.00(  0.13%)
                                          -0.0001  0.5293 -0.0334 -0.0013  0.0000
                                           0.0000 -0.7417 -0.0277  0.4042  0.0563
                                           0.0000  0.0000 -0.0252 -0.0247 -0.0070
               ( 63.32%)   0.7957* N  12 s( 36.56%)p 1.73( 63.41%)d 0.00(  0.03%)
                                          -0.0001  0.6046 -0.0037  0.0006  0.0000
                                           0.0000  0.7069  0.0132 -0.3659  0.0187
                                           0.0000  0.0000 -0.0107 -0.0129  0.0007

All C-C sigma bonds are contributed to equally by each carbon orbital. This orbital is a sp² hybridized orbital.

    1. (1.98249) BD ( 1) C   1 - C   2  
               ( 49.74%)   0.7053* C   1 s( 34.45%)p 1.90( 65.51%)d 0.00(  0.04%)
                                           0.0000  0.5869 -0.0086  0.0005  0.0000
                                           0.0000  0.7063  0.0290  0.3934 -0.0234
                                           0.0000  0.0000  0.0169 -0.0127  0.0004
               ( 50.26%)   0.7089* C   2 s( 34.72%)p 1.88( 65.23%)d 0.00(  0.04%)
                                           0.0000  0.5892 -0.0066  0.0009  0.0000
                                           0.0000 -0.6898  0.0068 -0.4184 -0.0371
                                           0.0000  0.0000  0.0122 -0.0159 -0.0045

Due to the sp² hybridization, there is a p orbital perpendicular to the plane that partake in pi bonding. This is contributed to more by one carbon. This is a consequence of including the electronegative nitrogen atom.

   3. (1.54875) BD ( 2) C   1 - C   5  
               ( 45.72%)   0.6762* C   1 s(  0.00%)p 1.00( 99.93%)d 0.00(  0.07%)
                                           0.0000  0.0000  0.0000  0.0000  0.9997
                                          -0.0036  0.0000  0.0000  0.0000  0.0000
                                          -0.0101  0.0241  0.0000  0.0000  0.0000
               ( 54.28%)   0.7367* C   5 s(  0.00%)p 1.00( 99.94%)d 0.00(  0.06%)
                                           0.0000  0.0000  0.0000  0.0000  0.9997
                                          -0.0080  0.0000  0.0000  0.0000  0.0000
                                           0.0228  0.0086  0.0000  0.0000  0.0000
   6. (1.61444) BD ( 2) C   2 - C   3  
               ( 52.23%)   0.7227* C   2 s(  0.00%)p 1.00( 99.94%)d 0.00(  0.06%)
                                           0.0000  0.0000  0.0000  0.0000  0.9997
                                          -0.0068  0.0000  0.0000  0.0000  0.0000
                                          -0.0159  0.0191  0.0000  0.0000  0.0000
               ( 47.77%)   0.6912* C   3 s(  0.00%)p 1.00( 99.94%)d 0.00(  0.06%)
                                           0.0000  0.0000  0.0000  0.0000  0.9995
                                          -0.0175  0.0000  0.0000  0.0000  0.0000
                                          -0.0153 -0.0196  0.0000  0.0000  0.0000

There is also a carbon nitrogen pi bond present, The nitrogen is also sp² hybridized meaning there is a p orbital perpendicular to the plane of the ring. Although this would normally contain 2 electrons (nitrogen has 5 valence electrons) by adding a positive charge to the molecule we have removed one of these. This means that a pi bond is able to form. The nitrogen p-orbital contributes 71.5% to the MO. Again this is due to the effects if electronegativity.

13. (1.82446) BD ( 2) C   4 - N  12  
               ( 28.54%)   0.5343* C   4 s(  0.00%)p 1.00( 99.83%)d 0.00(  0.17%)
                                           0.0000  0.0000  0.0000  0.0000  0.9991
                                           0.0132  0.0000  0.0000  0.0000  0.0000
                                           0.0394  0.0102  0.0000  0.0000  0.0000
               ( 71.46%)   0.8453* N  12 s(  0.00%)p 1.00( 99.98%)d 0.00(  0.02%)
                                           0.0000  0.0000  0.0000  0.0000  0.9999
                                           0.0036  0.0000  0.0000  0.0000  0.0000
                                          -0.0077 -0.0128  0.0000  0.0000  0.0000

The N-H bond, as expected, is contributed to more by the electronegative nitrogen atom.

   15. (1.98630) BD ( 1) H   9 - N  12  
               ( 25.41%)   0.5041* H   9 s( 99.88%)p 0.00(  0.12%)
                                           0.9994 -0.0064  0.0000  0.0000 -0.0342
               ( 74.59%)   0.8637* N  12 s( 26.82%)p 2.73( 73.15%)d 0.00(  0.02%)
                                          -0.0002  0.5178  0.0066 -0.0013  0.0000
                                           0.0000  0.0000  0.0000  0.8553 -0.0091
                                           0.0000  0.0000  0.0000 -0.0034  0.0153

The C-H bonds are contributed to 64.26% by the carbon sp² orbital with the remaining contribution form the hydrogen 1s orbital.

11. (1.98154) BD ( 1) C   4 - H  10  
               ( 64.26%)   0.8016* C   4 s( 33.44%)p 1.99( 66.52%)d 0.00(  0.04%)
                                           0.0004 -0.5780 -0.0180  0.0017  0.0000
                                           0.0000  0.6665 -0.0183 -0.4694  0.0193
                                           0.0000  0.0000  0.0164  0.0089 -0.0030
               ( 35.74%)   0.5978* H  10 s( 99.94%)p 0.00(  0.06%)
                                          -0.9997 -0.0018  0.0000 -0.0209  0.0128

Natural Bond Orbitals (Summary):

The C-N sigma bond is lowest in energy at -1.06555 AU. This is due to the fact that the polar covalent bond is the strongest present. The C-C sigma bond is the next lowest in energy, -0.90379 AU, as this is homo-nuclear, the overlap is great and so it is stabilized greatly. The N-H and C-H bonds are next in the sequence with the pi bonds being highest in energy. This is due to the fact that p-p overlap is poor an so the orbital is not stabilized as much. The N=C bond is lower in energy, -0.56810 AU. Again this is due to the electronegativity of the nitrogen. The C=C bond has an energy of -0.44892 AU.

Borazine B3LYP/6-31G(d,p)

Borazene is isoelectric with benzene. All of the C-H groups have been replaced by alternating B-H, N-H groups.

Optimization

An optimization was run on the molecule using B3LYP/6-31G(d,p.

Optimization file here

summary data

convergence

Jmol


     Item               Value     Threshold  Converged?
 Maximum Force            0.000001     0.000015     YES
 RMS     Force            0.000000     0.000010     YES
 Maximum Displacement     0.000004     0.000060     YES
 RMS     Displacement     0.000001     0.000040     YES

Optimized Borazine

The symmetry of the optimized molecule is D_3h. This is lower than the benzene molecule but higher than the boratabenzene and pyridinium molecules. The N-B bond length is 1.43 Å. This is in between that of a B-N single bond and B=N double bond, suggesting delocalization of the nitrogen lone pair. The boron-hydrogen bond lengths are greater than the nitrogen-hydrogen. This is due to poorer overlap and the fact that the difference in electronegativity of boron and hydrogen is smaller than that of nitrogen and hydrogen and thus the bond is not as polar, is weaker and longer.

Frequency

Frequency file here


Summary Data	Low Modes
	Low frequencies --- -4.0129 -3.9656 -2.8767 -0.0036 0.0035 0.0052 Low frequencies --- 289.7277 289.7282 404.5306

Again 30 vibrational modes were expected. Form the IR we can see that there are only 6 peaks present. There are more peaks present than observed for benzene because borazine has lower symmetry yet less than for boratabenzene and pyridinium because it has a higher symmetry, more of the vibrational modes are not IR active; they cause no change in dipole. There are also several degenerate peaks.

NBO Analysis

Population file here

NBO Analysis here

The N-H bond is contributed 71.9% by the nitrogen. This is due to the fact that it is a larger, more electronegative atom. This orbital has 22.8% s character and 77.2% p character. This is bonding with a hydrogen 1s orbital.

    3. (1.98494) BD ( 1) H   3 - N   6  
               ( 28.08%)   0.5299* H   3 s( 99.91%)p 0.00(  0.09%)
                                           0.9996 -0.0010 -0.0256  0.0148  0.0000
               ( 71.92%)   0.8481* N   6 s( 22.82%)p 3.38( 77.15%)d 0.00(  0.03%)
                                          -0.0002  0.4776 -0.0114  0.0006  0.7606
                                           0.0113 -0.4391 -0.0065  0.0000  0.0000
                                          -0.0105  0.0000  0.0000  0.0061 -0.0119

In contrast, the B-H bond is contributed to more by the hydrogen atom, 54.0%. this is due to the fact that the hydrogen is more electronegative than the boron.

   13. (1.98670) BD ( 1) B   7 - H   8  
               ( 45.97%)   0.6780* B   7 s( 37.47%)p 1.67( 62.47%)d 0.00(  0.07%)
                                          -0.0006  0.6120  0.0129 -0.0016  0.6841
                                          -0.0233  0.3950 -0.0135  0.0000  0.0000
                                           0.0204  0.0000  0.0000  0.0118 -0.0098
               ( 54.03%)   0.7351* H   8 s( 99.96%)p 0.00(  0.04%)
                                           0.9998  0.0002 -0.0166 -0.0096  0.0000

The boron-nitrogen sigma bond is contributed to 76.5% by the N orbital. This orbital is made up of 38.6% s character and 61.4% p character. The boron orbital has 31.3% s character and 68.5% p character. The nitrogen is the largest contributor to the bond due to the fact it is more electronegative.

    4. (1.98437) BD ( 1) N   4 - B   7  
               ( 76.47%)   0.8745* N   4 s( 38.55%)p 1.59( 61.44%)d 0.00(  0.01%)
                                           0.0000  0.6209  0.0043 -0.0001  0.7071
                                          -0.0001 -0.3379  0.0159  0.0000  0.0000
                                          -0.0057  0.0000  0.0000  0.0044 -0.0085
               ( 23.53%)   0.4851* B   7 s( 31.25%)p 2.19( 68.50%)d 0.01(  0.25%)
                                          -0.0003  0.5588 -0.0174  0.0032 -0.7259
                                          -0.0213  0.3933  0.0538  0.0000  0.0000
                                          -0.0360  0.0000  0.0000  0.0273 -0.0206

Both the nitrogen and boron atoms have a p-orbital perpendicular to the plane. This is able to take part in pi bonding. 88.2% of this pi bond is contribute by the nitrogen p-orbital. As well as the fact that the nitrogen is more electronegative, this is due to the fact the fact that the p-orbital on nitrogen contains a lone pair whilst the boron has an empty orbital. The nitrogen atom donates electron density into this orbital hence this is the major contributor to the bond.

    5. (1.82089) BD ( 2) N   4 - B   7  
               ( 88.21%)   0.9392* N   4 s(  0.00%)p 1.00(100.00%)d 0.00(  0.00%)
                                           0.0000  0.0000  0.0000  0.0000  0.0000
                                           0.0000  0.0000  0.0000  1.0000 -0.0003
                                           0.0000  0.0005 -0.0046  0.0000  0.0000
               ( 11.79%)   0.3433* B   7 s(  0.00%)p 1.00( 99.62%)d 0.00(  0.38%)
                                           0.0000  0.0000  0.0000  0.0000  0.0000
                                           0.0000  0.0000  0.0000  0.9976 -0.0315
                                           0.0000 -0.0573  0.0220  0.0000  0.0000

The B-N sigma bond is the lowest in energy at -0.68876 AU. This is followed by the N-H bond, then the B-H bond. The highest energy is the B-N pi bond. As previously discussed, the p-p overlap is poor and so the bond has a high energy.

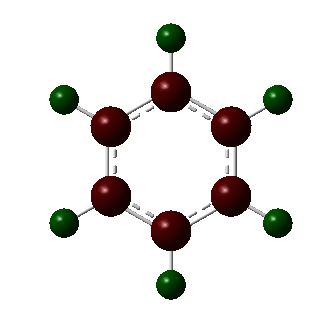
Charge Distribution Analysis

The charge distribution of all the molecules was viewed in the range -1.00 to 1.00 to allow for easy comparrison.


Benzene	Boratabenzene	Pyridinium	Borazine

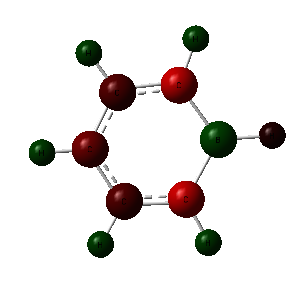
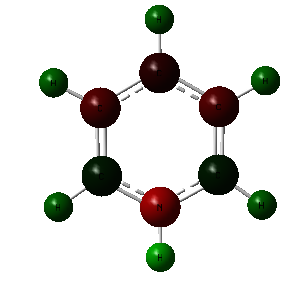
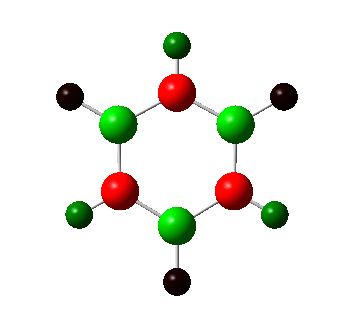
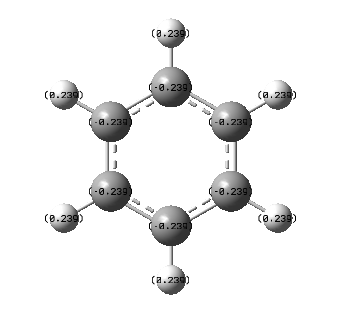
From the charge distribution analysis, we can see how exchanging a C-H group for a group containing a main group element effects the charge on the atoms. In benzene, due to the fact that the carbon is more electronegative than hydrogen, 2.55 compared to 2.2, we would expect to see a more negative carbon atom and more positive hydrogen atom. This is exactly what is observed; the charge on the carbon atoms is -0.239 depicted by the red colouring and hydrogen contains a charge of 0.239 with green colouring. The difference in electronegativity is small and so only a small difference in charge, and therefore colour occurs. Due to the symmetrical nature of the compound, all C-H units are the same.

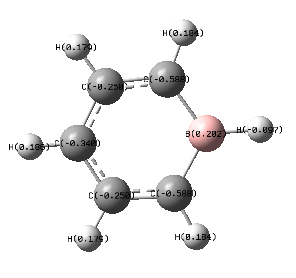
By replacing a C-H atom with boron we are introducing a more electropositive atom. This effects the charge distribution greatly; the boron atom has the most positive charge, at 0.202, shown in green, the hydrogen bonded to this has a negative charge due to the fact that it is more electronegative. Because, the difference in electronegativity is small, the charge difference, too is small, this is the reason for the dark colouring of the atoms. The carbon atoms adjacent to the boron are the most negatively charged at -0.588. This is due to the larger difference in electronegativity and so the carbon atom is better able to attract electrons and so experiences a more negative charge. This is shown by the red colour of this atom. The hydrogen atoms attached carry a positive charge. The two carbon atoms adjacent to these experience a more positive charge because of this effect, with the final carbon slightly higher than one might expect. The remaining hydrogen atoms are all more positive. Due to the small diffeence in electronegativity of carbon and boron, the colour changes are not that distinct.

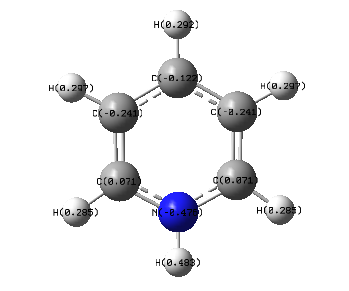
The pyridinium molecule contains a more electronegative atom, the nitrogen. This has a charge of -0.476 as expected, the most negative which can be seen by the red colour. Because of the difference in electronegativity, the hydrogen atom contains a high charge of 0.483. The adjacent carbons are more electropositive than nitrogen and so have electrons pulled away from them and therefore posses a positive charge of 0.071, shown by the green colour. Because the difference in electronegativity between carbon and nitrogen is smaller than that of hydrogen, the carbon atoms are dark in colour. The carbon atoms next to these have a more negative charge because of this. The remaining hydrogen atoms all have a positive charge.

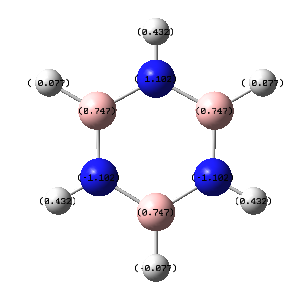
In the borazine all C-H units have been replace by alternating N-H and B-H units. Due to the fact that there is a large difference in electronegativity, the largest we have seen so far, there is a large difference in the charges observed, and bright colours shown. As expected, the more electronegative nitrogen possess the negative charge as it is able to draw electrons from both the neighboring boron atoms and hydrogen, seen by the bright red colour and charge of -1.102. The boron, bright green in colour has a charge of 0.747. The difference in electronegativity between boron and hydrogen is relatively small and so the hydrogens bonded to the boron are only slightly more negative and dark red in colour. The hydrogen atoms bonded to nitrogen posses a more positive charge and so are a more vivid green.

MO comparison


	Energy	Symmetry
Benzene	-0.35994 AU	a_2u
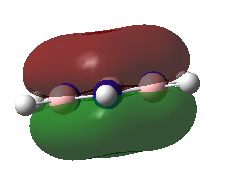
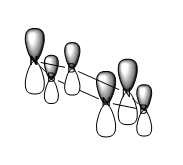
Borazine	-0.36134 AU	a"₂
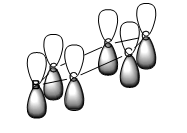
Boratabenzene	-0.13210 AU	b₁
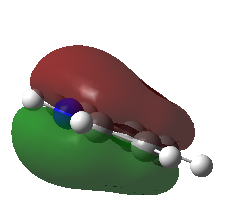
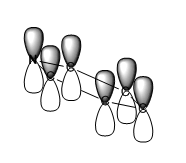
Pyridinium	-0.64062 AU	b₂

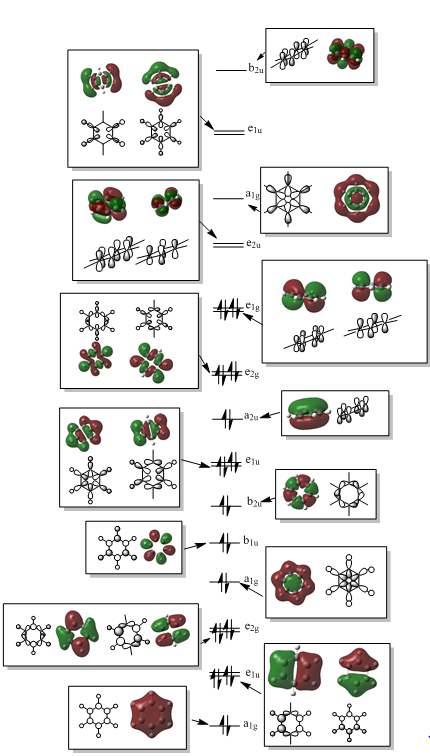
For all of the molecules, the fully bonding pi orbital is made up of the overlap of p-orbitals perpendicular to the plane of the ring. For benzene this orbital is contributed to equally by all atoms. In the pyridinium, the nitrogen p-orbital contributes more, this can be seen by the larger area over the nitrogen atom. In the boratabenzene, the carbon atoms contribute the most to the MO seen by the larger area above the carbons. In the borazine nitogen atoms are the larger contributor. This is due to the fact that the more stable atomic orbitals contribute most to the bonding MO.

The energy of the pyridinium MO is the lowest, this is due to the fact that it contains a nitrogen atom. In general, the more electronegative an atom, the lower in energy it is. Because of this, the energy of the whole molecular orbital is lowered. The p-p overlap of the carbon atoms is good, and the N-C p overlap is also quite good due to the similar size of the atoms. These things combined mean the energy of the MO is low.

The benzene and borazine MO are very similar in energy with the benzene being slightly higher in energy at -0.35994 AU and borazine -0.36134 AU. The borazine contains low in energy, electronegative nitrogen atoms and high in energy electropositive boron atoms. the effects of these two atoms balance out to give the energy of -0.36134 AU. The benzene molecular orbital is produced form the overlap of carbon p orbitals. Due to the fact that these are homo-nuclear interactions, the overlap is relatively good. The electronegativity of carbon lies in between boron and nitrogen and, therefore so does the energy. This means that the energy of the resulting MO, is in between that of the pyridinium and boratabenzene.

The boratabenzene MO has an energy of -0.13210 AU, the highest for the pi fully bonding orbitals. This is caused by the presence of a born atom, which is more electropositive than carbon and so brings the energy of the molecular orbital up.

In all of the molecules, this molecular orbital is the 17th occupied orbital and is non-degenerate, there is only one combination that gives fully bonding pi MO.


	Energy	Symmetry
Benzene	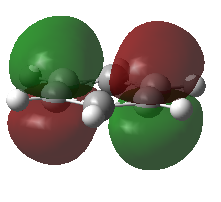-0.24690 AU	e_1g
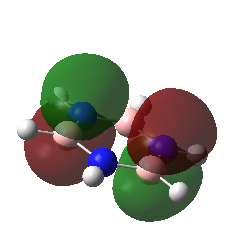
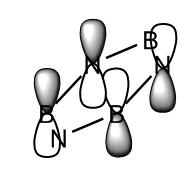
Borazine	-0.27594 AU	e"
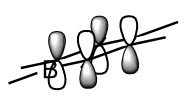
Boratabenzene	-0.03493	a₂
Pyridinium	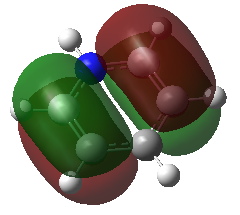-0.47886 AU	a₂

The second MO studied, was another pi orbital again contributed to, for all molecules, by p-orbitals perpendicular to the plane of the ring. This MO is higher in energy due to the through space anti-bonding interactions.

For benzene, boratabenzene and pyridinium, this MO is made up of the overlap of 2 carbon p-orbitals where as in borazine, this is the overlap of a nitrogen p-orbital and boron p-orbital. As the nitrogen is lower in energy it makes the biggest contribution to this MO.

Again we can see that the pyridinium MO has the lowest energy at -0.47886 AU due to the presence of the nitrogen atom. Borazine has the next lowest energy closely followed by the benzene. The boratabenzene is the highest in energy at -0.03493 AU.

For benzene and borazine, this orbital is degenerate. Both of these molecules have a higher symmetry than the boratabenzene and pyridinium and so degeneracy of the MOs occurs. The degenerate orbital involves the overlap of three p-orbitals instead of just two. The equivalent for pyridinium includes the nitrogen p-orbital resulting in the overall energy being lowered. For boratabenzene the inclusion of the boron atoms p-orbital increases the energy of the MO due to it's electropositive nature and higher energy. They are therefore not degenerate.

In benzene, pyridinium and borazine, this MO is the HOMO. However in boratabenzene, it is the 20th occupied MO (HOMO-1), there is a higher energy occupied MO for the reasons described previously.


	Energy	Symmetry
Benzene	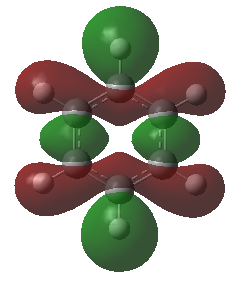-0.33960 AU	e_2g
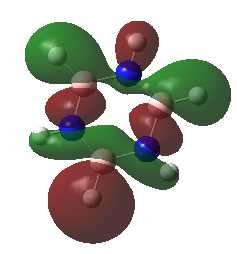
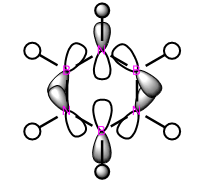
Borazine	-0.31991 AU	e'
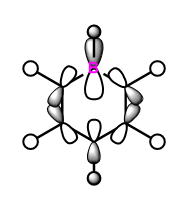
Boratabenzene	-0.09169 AU	a₁
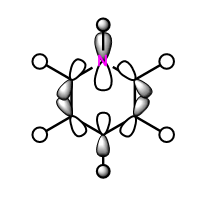
Pyridinium	-0.57433 AU	a₁

These anti-bonding sigma orbitals are made up of p-orbitals and hydrogen 1s orbitals. They have through bond, strong antibondong interactions and through space, weak bonding interactions. In the benzene, the carbon atoms all contribute to the MO equally as they are of the same energy. However for the other molecules, we can see that contribution by the atoms in the ring is not equal. The antibonding molecular orbital is contributed to more by the higher energy atomic orbital. In boratabenzene this is the boron atom, in pyridinium we see a larger contribution from the carbons atoms and in the borazine it is the born atom that contributes more. The different contribution is most noticeable in borazine, this is because the electronegativity, and therefore energy difference is the largest.

Again the pyridinium MO is the lowest in energy, followed by benzene, borazine and finally boratabenzene. The larger contribution from the boron atoms, means that the energy of the borazine MO is now higher than benzene.

For borazine and benzene, again this orbital is degenerate. The equivalent in boratabenzene is higher in energy and in pyridinium it is lower in energy. Because of this the MO is the 18/19 in borazine and benzene, 18th in boratabenzene and 19th in pyridinium.

Full MO comparison


Benezne	Borazine	Boratabenzene	Pyridinium

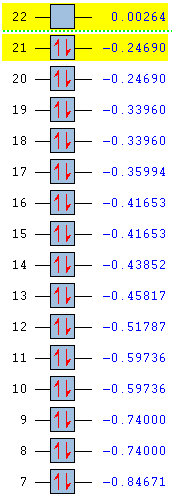
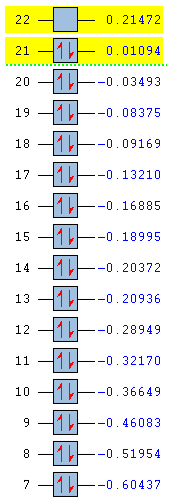
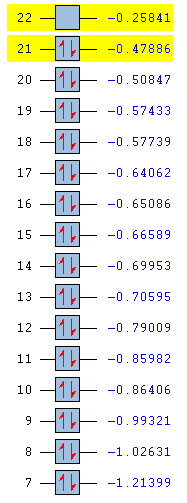
In substituting a C-H group in benzene, the energies of the molecular orbital are varied greatly. By introducing an electronegative atom, nitrogen, we see an overall decrease in energy for the pyridinium molecule. The introduction of an electropositive atom, boron, increases the overall energy of boratabenzene. In the borazine, all carbons have been replace by nitrogen or boron. From the MO we can see that energy starts off lower than benzene due to the effects of the nitrogen and ends higher than benzene due to the presence of boron. Borazine has the largest HOMO-LUMO gap and so is likely to be the most stable molecule. Boratabenzene is the least stable molecule, it has the highest energy and the smallest HOMO-LUMO gap.

The amount of degeneracy in the molecular orbitals is also greatly altered by the substitution of C-H groups. This is due to the changes in symmetry. The benzene and borazine have 5 sets of degenerate orbitals, although these aren't ordered in the same way in each molecule, whereas there are no degenerate orbitals in pyridinium and boratabenzene. This is due to the fact that, on substituting a c-H group in benzene, the symmetry is reduced from d_6h to C_2v. Symmetry in a molecule gives rise to degeneracy and so those molecules with low symmetry have no degeneracy of moleucular orbitals. Going form benzene to borazine also reduces symmetry to D_3h, however this is still high enough to induce degeneracy in the molecular orbitals.

As already seen, the ordering of the orbitals is also affected. This is due to the inclusion of main group atoms affecting the energy; the introduction of nitrogen in the MO moving them below and boron in the MO moving them above the corresponding orbitals in benzene.

Refereneces

↑ H. Burrows, R. Weir, J. Stohner Pure and Applied Chemistry, 1999, 71, 1919–1981 DOI:10.1351/pac199971101919
↑ ^2.0 ^2.1 ^2.2 W. M. Haynes, CRC Handbook of Chemistry and Physics, 2014, 95

[bond-1] H. Burrows, R. Weir, J. Stohner Pure and Applied Chemistry, 1999, 71, 1919–1981 DOI:10.1351/pac199971101919

[bondenthalpy-2] 2.0 ^2.1 ^2.2 W. M. Haynes, CRC Handbook of Chemistry and Physics, 2014, 95

[1]

[2]

Bonding and Molecular Orbitals in Main Group chemistry

EX3 Section

BH3:B3LYP/3-21G Optimization

BH3:B3LYP/6-31G(d,p)

GaBr3:B3LYP/LANL2DZ

BBr3:B3LYP/Gen

Geometry Comparison

Frequency Analysis

BH3:B3LYP/6-31G9(d,p)

GaBr3:B3LYP/LANL2DZ

Comparison

BH3 B3LYP/6-31G9(d,p) MO

NH3:B3LYP/6-31G(d,p)

Optimisation

Frequency Analysis

Population Analysis

NBO analysis

NH3BH3: B3LYP/6-31G(d,p)

Optimization

Frequency

Bond Energy

Project: Aromaticity

Benzene B3LYP/6-31g(d,p)

Optimization

Frequency

Population Analysis

NBO Analysis

Aromaticity

Boratabenzene B3LYP/6-31G(d,p)

Optimization

Frequency

NBO Analysis

Pyridinum B3LYP/6-31G(d,p)

Optimization

Frequency

NBO Analysis

Borazine B3LYP/6-31G(d,p)

Optimization

Frequency

NBO Analysis

Charge Distribution Analysis

MO comparison

Full MO comparison

Refereneces

EX₃ Section

BH₃:B3LYP/3-21G Optimization

BH₃:B3LYP/6-31G(d,p)

GaBr₃:B3LYP/LANL2DZ

BBr₃:B3LYP/Gen

BH₃:B3LYP/6-31G9(d,p)

GaBr₃:B3LYP/LANL2DZ

BH₃ B3LYP/6-31G9(d,p) MO

NH₃:B3LYP/6-31G(d,p)

NH₃BH₃: B3LYP/6-31G(d,p)