Rep:Mod:OneTrueCommunist

Simon Nizard, SA. RIdPEF.

Cope Rearrangement of 1,5-hexadiene

Introduction

Cope rearrangement

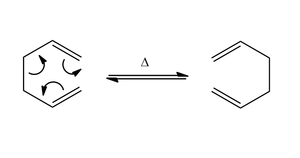
The (3,3) sigmatropic rearrangement of 1,5-hexadiene occurs via a via a chair-like transition state. Six (4n+2) electrons are involved and the reaction is thermally allowed via Hückel topology with suprafacial components. By virtue of being a pericyclic concerted reaction, there are no intermediates in the reaction coordinate.

We shall investigate the mechanism behind the rearrangement (which yields an identical product) and compare our results to literature calculations, which outlines two types of transition states: a loose-chair aromatic structure, and a slightly higher-energy boat transition state. Using Hartree-Fock calculation methods with the basis set 3-21G (HF/3-21G level of theory) and Density Functional Theory (Becke3 and Lee, Yang, Parr) with the 6-31G(d) basis set, we will optimize different conformers of 1,5-hexadiene to energy minima, using Gaussian09W and the High-Powered SuperComputer At Night (SCAN) systems for calculations.

Optimizing conformers of 1,5-hexadiene

Below is a table summarizing the optimizations of 1,5-hexadiene, as well as molecule symmetries (determined in GaussView5.0) and relative energies, which were in accordance with those previously calculated.

Conformer	Point Group	Energy/Hartrees (HF/3-21G)	Relative Energy (kcal.mol-1)
	C2	-231.68772	3.10
	C2	-231.69167	0.62
	C1	-231.69266	0.00
	C2	-231.68772	0.71
	C1	-231.69153	1.91
	C1	-231.68962	2.20
	C2	-231.69260	0.04
	Ci	-231.69254	0.08
	C2h	-231.68907	2.25
	C1	-231.69097	1.06

As can be seen, the lowest energy conformation calculated is the gauche 3, although with a primitive basis set such as 3-21G, the margin of error is quite large. The anti-1 and anti-2 are both within this error margin, which calls for a re-optimization using a more advanced basis-set of these three lowest conformations. Although the anti- conformations are expected to be lower in energy due to less strain, some gauche- conformations can benefit from the gauche effect, which favours hyperconjugation in some cases. The higher-level theory used was DFT/B3LYP 6-31G(d).

Conformer	Point Group	Energy/Hartrees (DFT/B3LYP/6-31G*)	Relative Energy (kcal.mol-1)
	C1	-234.61133	0.00
	C2	-234.61180	-0.30
	Ci	-234.61171	-0.24

Thus, with a higher accuracy, the anti- conformers are both lower in energy relatively than the gauche- conformer. All three structures are very similar in geometry to those calculated with HF/6-21G, but their energies are about 3 Hartrees lower overall, highlighting the differences between the calculations methods. To complete the tutorial and obtain thermochemical data for the molecule, we will now carry out a frequency analysis on the anti-2 conformer.

IR spectrum of C_i conformer

Frequency analysis of C_i anti-2 conformer

The frequency analyses were carried out at 6-31G(d) level of theory, and the calculation results can be found here and here for the one at 0K using the Freq=ReadIsotopes option in Gaussian. They yielded almost identical spectra, with a characteristic C=C stretching frequency at 1731 (sym) and 1734 (asym) cm^-1; no imaginary frequencies were calculated, meaning a local minimum had been found.

Thermochemical data

From the output files, the thermochemistry data was extracted and is shown below. . The first of these is the potential energy at 0 K including the zero-point vibrational energy (E = E_elec + ZPE), the second is the energy at 298.15 K and 1 atm of pressure which includes contributions from the translational, rotational, and vibrational energy modes at this temperature (E = E + E_vib + E_rot + E_trans), the third contains an additional correction for RT (H = E + RT) and the last includes the entropic contribution to the free energy (G = H - TS).

All energies in Hatrees

Temperature (K)	(Eelec + ZPE)	(E + Evib + Erot + Etrans)	(RT correction (H = E + RT))	(Entropic contribution (G = H - TS))
298.15	-234.469204	-234.461857	-234.460912	-234.500779
0	-234.468767	-234.461430	-234.460486	-234.500330

An extra calculation at 248°C (521.15 K) was carried to compare with the literature value of the E_elec + ZPE: -234.46877 Ha [lit: -234.46925 Ha] The thermal energy of the 0K measurements is lower than that of room temperature, which is logical and confirms that the basis set works for this molecule (the results are consistent).

Optimizing the "Chair" and "Boat" Transition Structures

In this section, we optimize transition structures using three methods: 1) computing force constants, 2) frozen coordinate method and 3) the QST2 method. We shall briefly expand on these in turn, and also analyse an IRC (intrinsic reaction coordinate) pathway for the Cope-rearrangement.

Optimisation of Chair TS structure using Berny method

Cope rearrangement chair

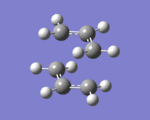
Two allyl CH₂CHCH₂ fragments were optimised using HF/3-21G levels of theory, and were approached together to create a reasonable guess for the chair transition state structure, with the terminal C atoms of each allyl group approximately 2.20 Å apart. Optimising to a Berny TS using first HF/3-21G and then DFT/B3LYP/6-31G(d) levels of theory, and calculating force constants only once yielded an optimized transition state: [bond-forming distances: 2.02 Å]. One imaginary frequency was observed at -818 cm^-1, which one can visualize by clicking on the thumbnail (left). Calculation.

Optimisation of Chair TS structure using Frozen coordinate method

The frozen coordinate method was applied as per outlined protocol: the terminal carbon atoms in the allyl fragments were fixed at 2.20 Å, and the rest of the molecule optimised at HF/3-21G level; the bonds are then unfrozen and the molecule optimized to a transition state (Berny) using the same level of theory. Again, bond distances were 2.02 Å. The two steps of the calculation can be found here and here.

The TS obtained was further optimised using force constants at DTF/B3LYP/6-31G(d), and this time the bond distance was 1.97 Å, and the frequency of the imaginary vibration located at 525 cm^-1. Calculation.

Optimisation of Boat TS structure using QST2 method

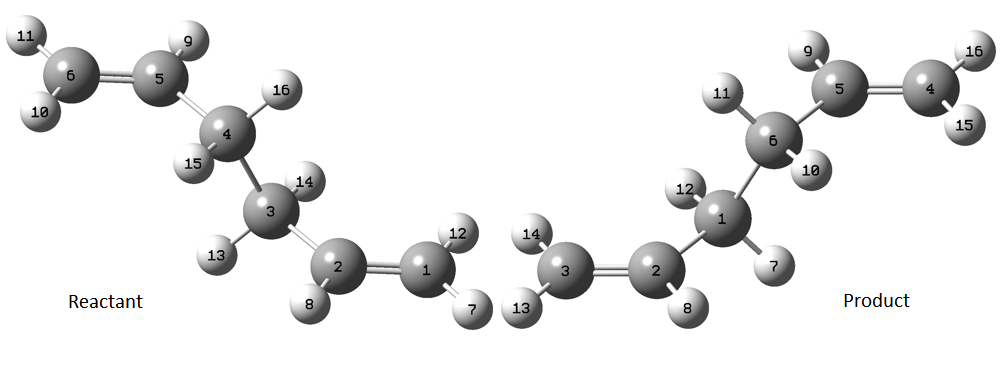
The reactant and product were both specified using atom-labelling, in order to proceed with the QST2 method, and the calculation would interpolate between the two structures to try and find the transition state between them. This labeling is shown above, and was followed up with a rearrangement of the carbon-carbon angles to give two eclipsed structures (C-C-C-C dihedral angle = 0°, C-C-C angles: 100°), shown below:

Vibration at -840cm^-1 in Boat C_2h Transition State

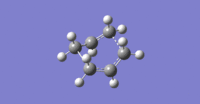
This led to a correct boat-like transition structure with an imaginary vibration at -840 cm^-1, shown right, which clearly shows one bond forming as the other dissociates (click to view animation). The resulting calculation can be found here. Bond breaking/forming distances were 2.14 Å this time, slightly longer than for the chair TS.

Intrinsic Reaction Coordinate

The IRC allows us to investigate the step-by-step progress and follow the minimum energy path from a transition structure down to its local minimum on a potential energy surface. The chair TS structure was analysed in this fashion, using 50 calculation points and calculating the force constants only once at first. This yielded an incomplete optimization, and the procedure was repeated but this time with recalculation of force constants at every step. Graphs are shown below.

first IRC (constants calculated once)

Energy vs. IRC	RMS vs. IRC

second IRC (constants calculated every step)

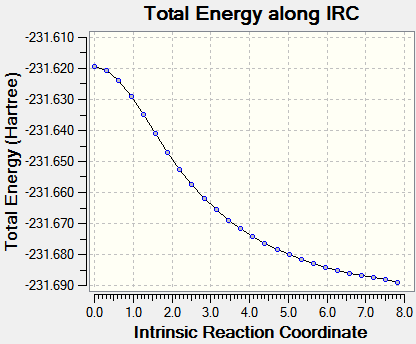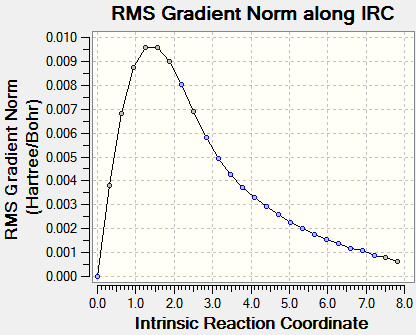
Energy vs. IRC	RMS vs. IRC

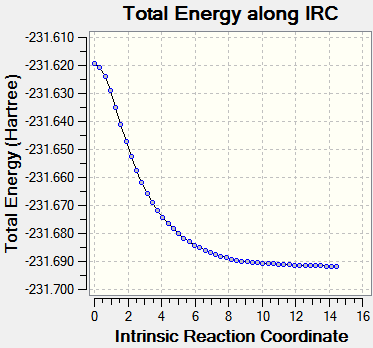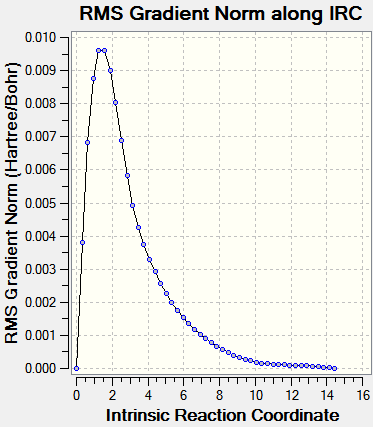
The IRC calculations both ended after 47 iterations and were calculated only in the forward direction (since the reaction coordinate is symmetrical. Above on the right is the structure of the energy minimum at step 47, and its Jmol is shown below. C--C Bonds: 1.31 Å, 1.51 Å, 1.55 Å.

Transition State Activation Energies

In order to calculate the transition state activation energies, the lowest-calculated energy conformations of 1,5-Hexadiene were compared with the chair and boat transition state energies for both the HF/3-21G and DFT-B3LYP/6-31G* levels of theory. The anti-2 conformer was taken as the reference energy, using values determined in section 1.3.1 of this report.

Summary of energies (in hartree)

	HF/3-21G			B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Reactant (anti 2)	-231.428978	-231.285044	-231.279625	-234.611708	-234.469203	-234.461857
Chair TS	-231.619322	-231.466700	-231.461340	-234.556983	-234.414928	-234.409006
Boat TS	-231.602802	-231.450928	-231.445299	-234.543093	-234.402338	-234.396004

Summary of activation energies (in kcal/mol)

	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Lit., Exp.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)	114.0	114.1	34.06	33.17	33.5 ± 0.5 ; 34.2
ΔE (Boat)	13.77	103.4	41.96	41.32	44.7 ± 2.0 ; 42.0

• 1 hartree = 627.509 kcalmol^-1

These results clearly show how much more accurate the DFT-B3LYP/6-31G* level of theory is compared to the HF/3-21G as they match better with the literature and experiment. The results also show the activation energy of the boat conformation to be slightly higher than that of the chair, which is also predicted experimentally.

Diels Alder Cycloaddition

Introduction

In this section, the concerted Diels Alder cycloaddition will be investigated using semi-empirical methods and Hartree-Fock levels of theory. The reaction involves the concerted movement of 4 + 2 π-electrons, and follows a Hückel-suprafacial reaction pathway, with a single transition state. It is typically carried out between a conjugated diene and a substituted dienophile. To start with we shall analyse the simplest form of the reaction: cis-butadiene and ethylene; after which we shall take a look at the stereochemistry governing the reaction, in the 1,3-cyclohexadiene addition to maleic anhydride and attempt to rationalise the experimentally-observed ratios of kinetic and thermodynamic products.

cis-Butadiene

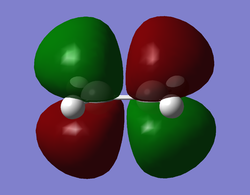
The molecule was sketched out in GaussView5.0 and optimized using AM1 semi-empirical level of theory. The same was done for ethylene. The HOMO and LUMO of each molecule were mapped out and are shown in the table below, along with appropriate symmetry assignations with respect to the reflection symmetry plane.

HOMO Ethene (Symmetric)	LUMO Ethene (Antisymmetric)	HOMO cis-Butadiene (Antisymmetric)	LUMO cis-Butadiene (Symmetric)

Since only orbitals with the same symmetry can interact due to the principle of symmetry conservation, we will see HOMO-LUMO interactions between the molecules during the cycloaddition. The cycloaddition follows a normal electron demand Diels-Alder involving an electron rich diene and an electron-poor dienophile. Therefore the important MO interaction is that of the HOMO of cis-butadiene (diene) with the LUMO of ethylene (dienophile), which is allowed due to having the same symmetry.

Cycloaddition Transition state of the prototypical reaction

The frozen coordinate method proved to give the most satisfying results. Positions of the terminal carbon atoms were fixed at 2.1 Å, and the rest of the molecule optimized. The second step involved unfreezing the above bonds, and optimizing them. This was carried out first using HF/3-21G levels of theory, and further optimised (and a frequency analysis carried out to confirm transition states through the presence of one imaginary vibration) using DFT/B3LYP/6-31G(d) levels of theory. HF/3-21G (first step), HF/3-21G (step two), HF/3-21G freq analysis, B3LYP freq+opt.

Level of Theory	Calculated Frequency (cm-1)	Animation (click to view)	Bond Lengths [Lit] (Å)
DFT-B3LYP/6-31G*	-525		Butadiene: 1.38 [1.34]; 1.41 [1.48]; Ethene: 1.38 Terminal C-C separation = 2.27
HF/3-21G	-818		Butadiene: 1.37 [1.35]; 1.40 [1.46]; Ethene: 1.38 Terminal C-C separation = 2.20

As can be seen from the frequency calculations, we are in the presence of two transition states. The vibrations indicate synchronous formation of the bonds, further confirming the cycloaddition/pericyclic nature of the Diels-Alder reaction.

The bond-lengths are respectively shorter and longer than those in stable ground-state cis-butadiene, which makes sense since the transition state is an unstable structure. It is noted that the intermolecular separation is larger when using a more rigid calculation method; however, in both structures, the separation is smaller than the doubled van der Waals radius of carbon (3.40 Å), which indicates the formation of a C-C σ bond.

The lowest "real" frequency (click to view) calculated was at 136 cm^-1, and shows a twisting motion that, if it were the reaction pathway, would indicate asynchronous formation of bonds (and thus some sort of intermediate between two transition states).

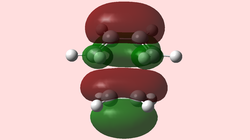
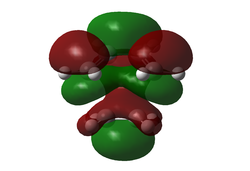
MO analysis

Generated from the DFT/B3LYP/6-31G(d) optimized structure.

HOMO TS (Symmetric)	LUMO TS (Symmetric)

The symmetrical nature of the HOMO is surprising, since it is an orbital that arises from the interaction of two anti-symmetric oribtals (see normal electron demand above). Note that the HOMO-1 yields an anti-symmetrical MO for the transition state, and is very close in energy to the HOMO. This leads us to believe that the theory might break down for such calculations, predicting the incorrect energy order of the orbitals. Click here to view the HOMO-1 orbital

IRC analysis of the reaction

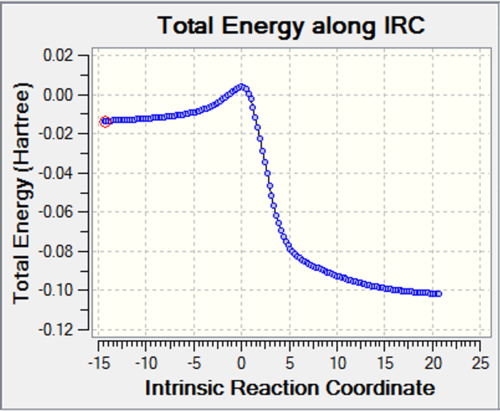
The IRC analysis of the reaction was carried out to investigate the transition state structure in more detail. However, it could only be carried out at HF/3-21G levels of theory. The formatted checkpoint file can be found here. Below are shown the energy and RMS gradient graphs for the 71-step IRC calculation, calculated both ways. The top of the energy curve is the fleeting TS, which is step 51 on the IRC pathway.

cis-butadiene+ethene TS IRC (constants calculated every step)

Energy vs. IRC	RMS vs. IRC

The IRC shows a smooth transition with a 2.21 Å intermolecular (at terminal carbons) separation at the highest energy step. The end-structure (cyclohexene) showed bond-lengths which agreed with the literature, with C=C: 1.32 Å, C-C: 1.51, 1.55, 1.56 Å.

Diels-Alder reaction of maleic anhydride and 1,3-cyclohexene

The two different products of this reaction are shown on the right. The exo- product is more thermodynamically stable and forms slowly but surely. The endo-product is the kinetic product, and typically forms faster and at lower temperatures. In thi section, we will investigate the transition state of these two reaction mechanisms, and attempt to rationalise the relative stabilities of the two products and TStates through an MO analysis. It has been reported that secondary orbital interactions from substituents on the diene can interact and stabilise the system in the endo- product, and we shall endeavour to see if these can outweigh the steric hindrance of the endo-form.

Molecular orbitals of the reactants

The MO's were generated from HF/3-21G optimized molecules. cyclohexene calc. and maleic anhydride calc.

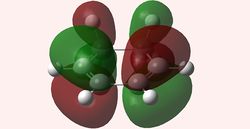
HOMO Maleic anhydride (Symmetric)	LUMO Maleic anhydride (Antisymmetric)	HOMO 1,3-Cyclohexadiene (Antisymmetric)	LUMO 1,3-Cyclohexadiene (Symmetric)

Here, due to the EWG substituents (terminal and bridging oxygens), maleic anhydride is an electron-poor dienophile, which means the HOMO of 1,3-cyclohexadiene will interact with the LUMO of maleic anhydride. The reaction is allowed, since both have the same symmetry.

Optimisation of transition states

Using HF/3-21G levels of theory and the pre-optimized reactants shown above, the frozen coordinated method was applied to the Diels-Alder reaction. Click to view animations. The .chk files obtained from the calculation exceed 2MB and cannot be uploaded on the wiki. As such, the .log output files are shown here (exo) and here (endo).

Approach	Calculated Frequency (cm-1)	Animation (click to view)
Exo	-757
Endo	-806

The imaginary frequencies show a synchronous bond formation on both terminii of the molecules, confirming the concerted nature of the cycloaddition.

From the energies of the optimizations, it is too uncertain to predict the ordering of the transition states in terms of activation energies, even at HF/3-21G levels of theory.

MO analysis of Transition states

From the optimized structures the HOMOs were generated, and are discussed below.

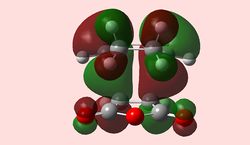
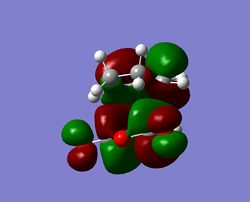
HOMO exo-TS (Antisymmetric)	LUMO exo-TS (Antisymmetric)	HOMO endo-TS (Antisymmetric)	LUMO endo-TS (Antisymmetric)

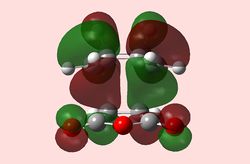
As in the prototypical example above, the two anti-symmetrical orbitals have combined into two anti-symmetrical HOMOs, with a nodal plane going down the plane of reflection of the Transition state. At first glance, the HOMO does not show any secondary orbital interactions; but a quick interpretation of the LUMO shows the π* antibonding orbitals of the carbonyl substituents interacting with the rest of the molecule, bringing down its energy relative to the steric hindrance of the endo-conformation. This secondary stabilisation on the endo-TS may explain why the endo-product can form, but does little to explain why it is favoured over the exo-TS, since it exhibits it as well.

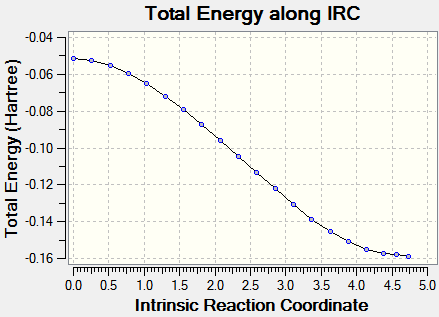
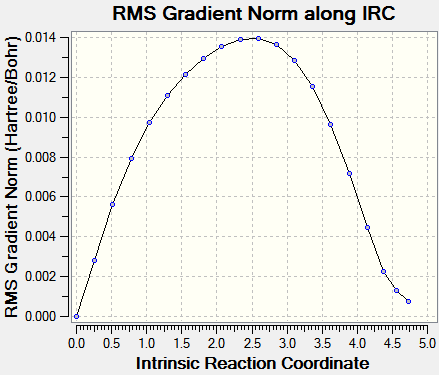
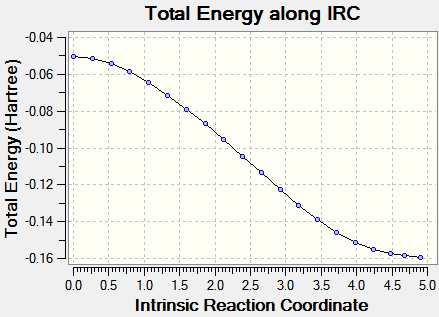
IRC pathways analysis

IRC analysis was carried with mitigated success: it proved impossible to carry it out until complete minimization; the output files are provided (.chk files being too large to upload to the wiki)here (exo) and here (endo). The calculations were carried out with AM1 semi-empirical level of theory. Input demand: backwards and forwards; output: only forwards.)

maleic anyhdride + 1,3-cyclohexene ENDO TS IRC (constants calculated every step)

Energy vs. IRC	RMS vs. IRC

maleic anyhdride + 1,3-cyclohexene EXO TS IRC (constants calculated every step)

Energy vs. IRC	RMS vs. IRC

maleic anyhdride + 1,3-cyclohexene ENDO TS and EXO TS animations

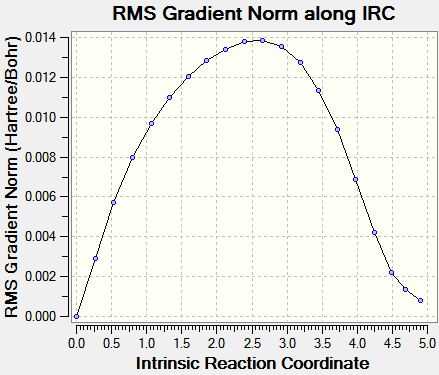
exo	endo

Although an imperfect structure, the MOs of the last step on the IRC are shown below in an attempt to locate secondary orbital interactions. None are found; however, it is of note that the HOMO for the endo product is symmetrical, which highlights again the insufficiencies of AM1 calculation methods, which are too primitive.

maleic anyhdride + 1,3-cyclohexene ENDO TS and EXO TS minima

exo	endo

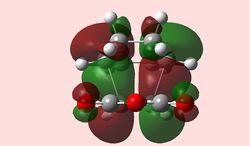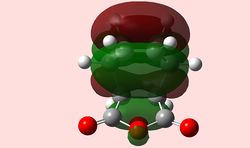
Thus, this exercise has shown us the basics of computational physical chemistry, introducing the powerful tool of IRC pathway calculations to get a reaction coordinate vs. energy graph and begin working out ΔG for the diels Alder cycloaddition. However, the AM1 was too basic a basis set to really delve into the large molecule of the maleic anhydride+1,3-cyclohexene transition state.