Rep:Mod:OliviaPini
Molecule 1 - Ammonia
General Information
The molecule is ammonia.
The calculation method is RB3LYP.
The basis set is 6-31G(d.p).
The final energy (E(RB3LYP)) is -56.55776873 a.u.
The RMS gradient is 0.00000485 a.u.
The point group of the molecule is C3V
The optimized bond distance is 1.01798 angstrongs.
The optimized H-N-H bong angle is 105.741.
Item Box
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES Predicted change in Energy=-5.985969D-10 Optimization completed.
Jmol of molecule
ammonia |
The optimisation file is linked to here
Vibrational analysis
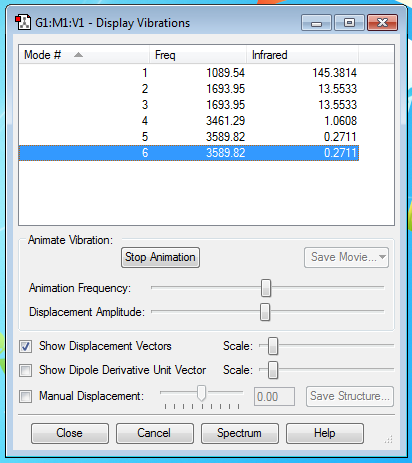
From the 3N-6 rule you would expect 6 modes of vibrations.
The second and third modes are degenerate as are the last two, as they have identical energies.
The first, second, third modes are bending. Whereas, the fourth, fifth and sixth modes are all stretching.
The mode that is highly symmetric is the fourth mode.
The first mode is the one that is known as the "umbrella mode".
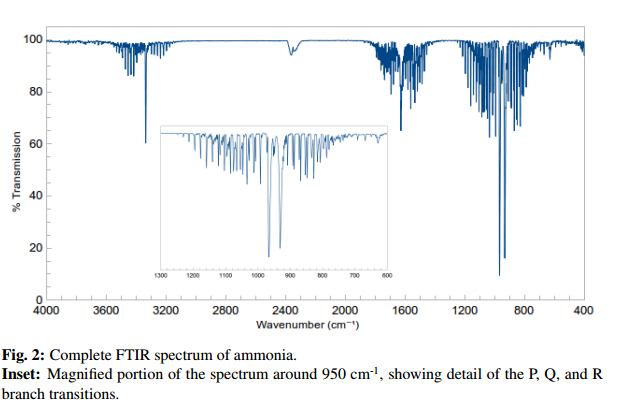
You would expect to see three bands in the experimental spectra of gaseous ammonia.
This FTIR spectrum shows three bands, as was predicted from the vibration analysis. The bands also occur at wave numbers similar to those predicted above. This supports the fact that the molecule is properly optimized, as the value match those of the literature. Each band is made up of a selection of lines due to the presence of different rotational levels being occupied.
Charges
You would expect the nitrogen to have a negative charge in comparison to the hydrogen's, as it is a more electronegative atom. This means the nitrogen has more tendency to pull electron density towards itself in a bond, hence the negative charge. The charge on the nitrogen found during this investigation was -1.125, and that on the hydrogen's is 0.375.
Molecule 2 - Nitrogen
General Information
The molecule is nitrogen.
The calculation method is RB3LYP.
The basis set is 6-31G(D.P).
The total energy is -109.52412868 a.u.
The RMS gradient is 0.00000060 a.u.
The point group of the molecule is D∞h
The optimized bond distance is 1.10550 angstrongs.
The optimized bong angle is 180.
Item Box
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.401090D-13
Optimization completed.
-- Stationary point found.
Jmol of molecule
nitrogen |
The optimization file is linked to here
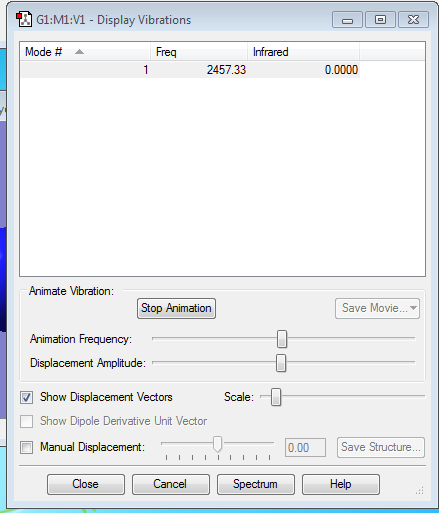
Vibration Analysis
As can be seen in the image, there are no negative frequencies.
Molecule 3 - Hydrogen
General Information
The molecule is hydrogen.
The calculation method is RB3LYP.
The basis set is 6-31G(d.p).
The total energy is -1.17853936 a.u.
The RMS gradient is 0.00000017 a.u.
The point group of the molecule is D∞h
The optimized bond distance is 0.74279 angstrongs.
The optimized H-N-H bong angle is 180.
Item Box
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.164080D-13
Optimization completed.
-- Stationary point found.
Jmol of molecule
hydrogen |
The optimisation file is linked to here
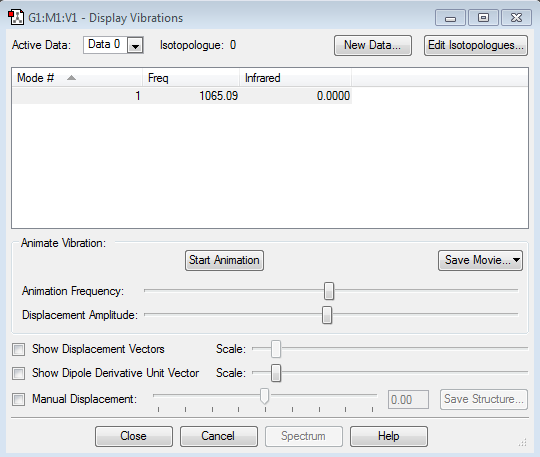
Vibration Analysis
Energy of Haber-Bosch reaction
E(NH3)= -56.55776873 a.u. = -148492.4218 KJ/mol
2*E(NH3)= -113.1155375 a.u. = -296984.8436 KJ/mol
E(N2)= -109.52412868 a.u. = -287555.5998 KJ/mol
E(H2)= -1.17853936 a.u. = -3094.25509 KJ/mol
3*E(H2)= -3.53561808 a.u. = -9282.765269 KJ/mol
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.05579074 a.u.= -146.478531 KJ/mol
Literature values for this is ΔH=-92.4 kJ/mol (2), which varies quite significantly from the calculated value. This is because the literature value was calculated in a real life system and so under 500 atm pressure, 400-450 degrees centigrade and using an iron catalyst. Whereas the calculated value was at standard conditions.
Own Molecule - Fluorine
General Information
The molecule is fluorine.
The calculation method is RB3LYP.
The basis set is 6-31G(d.p).
The total energy (E(RB3LYP)) is -199.49825218 a.u.
The RMS gradient is 0.00007365 a.u.
The point group of the molecule is D∞h
The optimized bond distance is 1.40281 angstrongs.
The optimized F-F bong angle is 180.
Item Box
Item Value Threshold Converged?
Maximum Force 0.000128 0.000450 YES
RMS Force 0.000128 0.000300 YES
Maximum Displacement 0.000156 0.001800 YES
RMS Displacement 0.000221 0.001200 YES
Predicted change in Energy=-1.995025D-08
Optimization completed.
-- Stationary point found.
Jmol of molecule
fluorine |
The optimization file is linked to here
Vibration Analysis
Fluorine is a dihomonuclear molecule, so would have no charge.
Molecular Orbitals
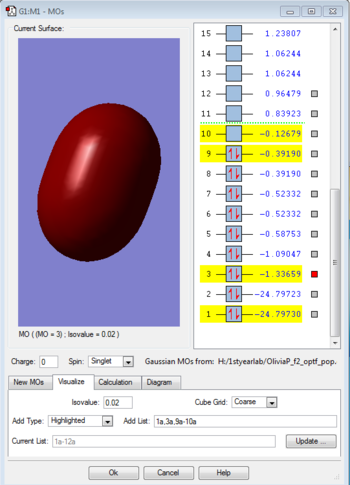
This is a sigma bonding orbital and the AOs that contribute to it are a 2S orbital from each of the fluorine atoms, which are combining in phase. It is an orbital that is deep in energy, as it is only the second bonding orbital. It is fully occupied, with two electrons with paired spins.
This is a sigma anti-bonding orbital and the AOs that contribute to it are a 2S orbital from each of the fluorine atoms, however they are combining out of phase. It is an orbital that is deep in energy, as it is only the second anti-bonding orbital, and is also deeper in energy then all the corresponding bonding and anti-bonding orbitals for the p orbital combinations. It is fully occupied, with two electrons with paired spins.
This is a sigma bonding orbital and the AOs that contribute to it are a 2Pz orbital from each of the fluorine atoms, which are overlapping head on in phase, along the axis of the bond. It is an orbital that is deep in energy, as it is only the third bonding orbital, although it is less deep in energy (higher in energy) then the above bonding and anti bonding orbitals. It is fully occupied, with two electrons with paired spins.
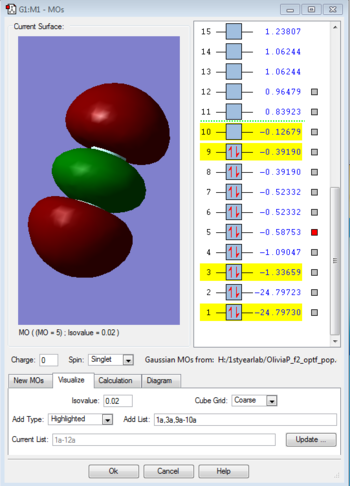
This is a pi bonding orbital and the AOs that contribute to it are a 2Px orbital from each of the fluorine atoms, which are overlapping side one in phase,with electron density above and below the axis. It is an orbital that is quite deep in energy, although it is less deep in energy (higher in energy) then all the above orbitals. It is fully occupied, with two electrons with paired spins.
This is a sigma anti-bonding orbital and the AOs that contribute to it are a 2Pz orbital from each of the fluorine atoms, which are overlapping head on out of phase. It is an orbital that is not deep in energy but high in energy, as it the LUMO, and hence it is not occupied.
References
1. Melville, J. Infrared Spectroscopy and Interferometry as Methods for Structural Determination of Ammonia. (1995).
2. Clark, J. Case Study: The Haber Process. Chemistry LibreTexts (2017). Available at: https://chem.libretexts.org/Core/Physical_and_Theoretical_Chemistry/Equilibria/Case_Studies/Haber_Process. (Accessed: 3rd March 2017)