Rep:Mod:OPBINORG
EX3 Section
BH3
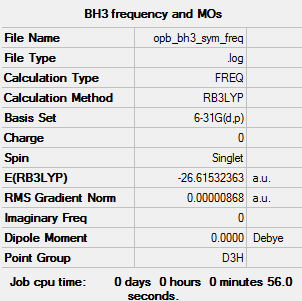
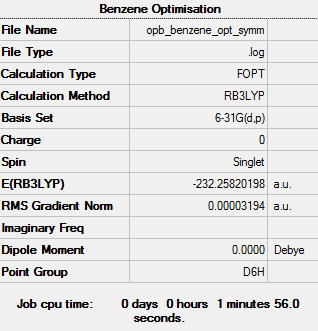
Initially a B3LYP/3-21G "rough" optimisation was used. Following this a B3LYP/6-31G(d,p) optimisation was used to get the molecule into its lowest energy structure. The summary table for the molecule after both optimisations is shown below.
The item table, confirming the completion of optimisation shows that the forces have converged:
Item Value Threshold Converged? Maximum Force 0.000017 0.000450 YES RMS Force 0.000009 0.000300 YES Maximum Displacement 0.000068 0.001800 YES RMS Displacement 0.000034 0.001200 YES
Using this optimised molecule file, a B3LYP/6-31G(d,p) frequency Gaussian calculation was run to confirm that the structure is a minima in energy. The resulting can be found here: File:OPB BH3 SYM FREQ.LOG
The low frequencies from this file are given by the table below. The first line of frequencies are the '- 6' vibrations from the '3N - 6' non-linear molecule number of vibrations rule. These vibrations are close to zero, where as the second give frequencies that are observed in vibrational spectroscopy.
Low frequencies --- -10.1111 -3.0903 -0.0054 0.4892 1.8274 3.5901 Low frequencies --- 1162.9534 1213.1537 1213.1564
The next table gives a list of all vibrations in the molecule and characterises them. In the IR spectrum for BH3 (which is given below the vibration table) there are less peaks than individual vibrations that the molecule possesses (six). This is because there are two degenerate pairs of wavenumbers, at 1213 cm-1 and 2716 cm-1 where only one signal is observed at each wavenumber. As well as this, the symmetric stretch at 2582 cm-1 does not result in a change in dipole moment, and thus due to the selection rules of IR spectroscopy, is not observed as it is IR inactive. This results in three peaks in the spectrum.
| wavenumber /cm-1 | Intensity /(arbitrary units) | symmetry | IR active? | type |
| 1163 | 93 | A2 | yes | out-of-plane bend |
| 1213 | 14 | E' | very slight | bend |
| 1213 | 14 | E' | very slight | bend |
| 2582 | 0 | A1' | yes | symmetric stretch |
| 2716 | 126 | E' | yes | asymmetric stretch |
| 2716 | 126 | E' | yes | asymmetric stretch |
Optimised BH3 |
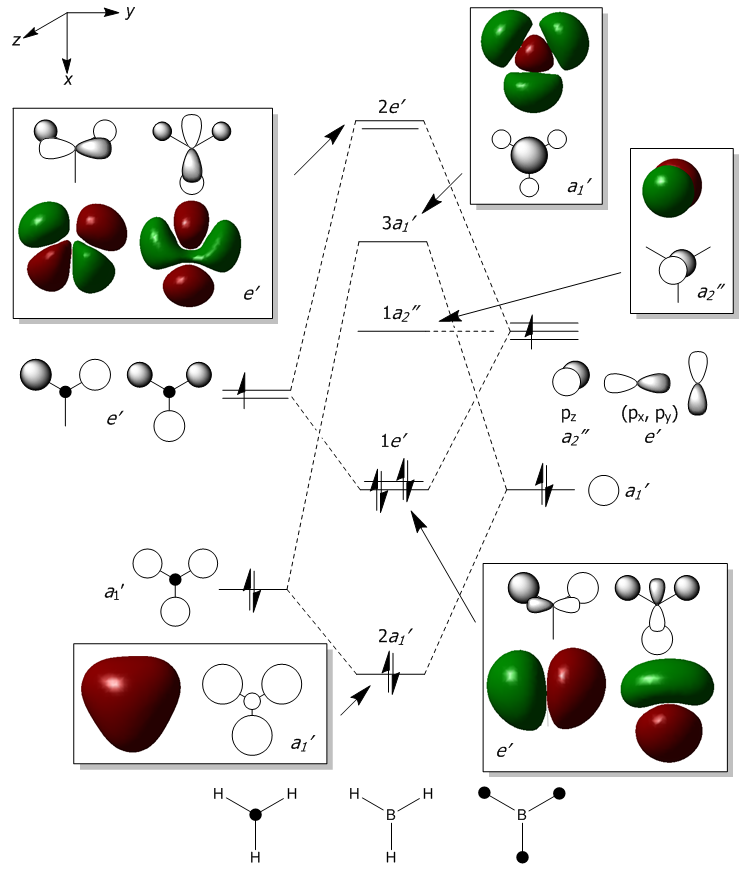
The molecular orbitals were calculated and are compared with the theoretically expected orbitals below. The lowest energy orbital is not shown in the diagram as it is too deep in energy, it is an unbonding ## orbital formed from the 1s orbital of boron. For all of these orbitals, the computed looks very similar to those created using the linear combination of molecular orbitals. This shows that the calculations being used to measure these MOs is very accurate. The only orbital that looks different is 3a1, in the computed orbital, there is a lobe at the centre on the boron that comes out of the page (x-axis) whereas LCAO shows that it should be a spherical lobe. This difference could have come from the B3LYP/6-31G(d,p) basis set which incorporates a d-orbital onto the boron.
Smf115 (talk) 00:12, 23 May 2018 (BST)Clear inclusion of the MOs into the diagram and notice of both the similarties and differences. Good consideration of the effect of the basis-set on the calculated MOs but when comparing to the qualitative LCAO approach this isn't quite relevant. The LCAO approach is limited in being unable to predict the exact contributions of the AOs and the calculated MO shows a larger contribution from the H than expected.
NH3
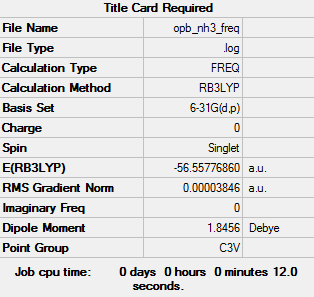
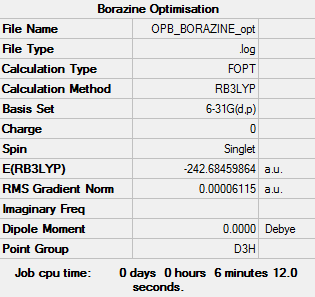
Similar to before the molecule underwent B3LYP/6-31G(d,p) optimisation and frequency calculations, the results are given below.
Item Value Threshold Converged? Maximum Force 0.000098 0.000450 YES RMS Force 0.000038 0.000300 YES Maximum Displacement 0.000384 0.001800 YES RMS Displacement 0.000130 0.001200 YES
log file File:OPB NH3 FREQ.LOG
Low frequencies --- -31.2509 -31.2375 -3.3206 -0.0036 0.0078 0.0696 Low frequencies --- 1088.6130 1694.0203 1694.0207
Optimised NH3 |
NH3BH3
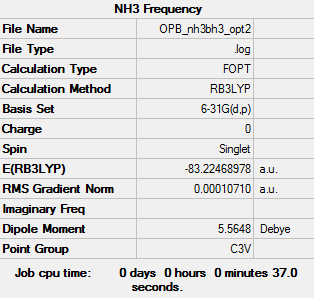
Item Table
Item Value Threshold Converged? Maximum Force 0.000110 0.000450 YES RMS Force 0.000065 0.000300 YES Maximum Displacement 0.000934 0.001800 YES RMS Displacement 0.000327 0.001200 YES
log file File:OPB NH3BH3 FREQ.LOG
Low frequencies --- -0.0016 -0.0015 -0.0012 5.5552 18.5117 27.1650 Low frequencies --- 264.8215 632.8824 639.6197
Optimised BH3NH3 |
The energy of the N-B bond is calculated by subtracting the energy of the substituent parts (NH3 and BH3) from the total energy of the molecule. This is shown below:
E(BH3) = -26.61532 a.u.
E(NH3) = -56.55777 a.u.
E(NH3BH3) = -83.22468 a.u.
ΔE = E(NH3BH3) - [E(NH3) + E(BH3)] = -0.05159 a.u. = -129 kJ mol-1
For reference, a common C-C single bond has a dissociation energy of about 350 kJ mol-1, so despite there being a difference in electronegativity between B and N which is not present in C-C bonds, our calculated bond is still weaker.
BBr3
Item Value Threshold Converged? Maximum Force 0.000027 0.000450 YES RMS Force 0.000012 0.000300 YES Maximum Displacement 0.000137 0.001800 YES RMS Displacement 0.000073 0.001200 YES
Low frequencies --- -5.0658 -3.1603 -2.2411 -0.0001 -0.0001 0.0002 Low frequencies --- 155.8568 155.9403 267.7009
The frequency calculated file for this molecule can be found at: DOI:10042/202398
Optimised BBr3 |
Aromaticity Investigation
Benzene
Maximum Force 0.000080 0.000450 YES RMS Force 0.000014 0.000300 YES Maximum Displacement 0.000203 0.001800 YES RMS Displacement 0.000042 0.001200 YES
Low frequencies --- -0.0088 -0.0041 -0.0041 13.4708 13.4708 17.1862 Low frequencies --- 414.4052 414.4052 621.2116
Optimised Benzene |
Borazine
Item Value Threshold Converged? Maximum Force 0.000083 0.000450 YES RMS Force 0.000031 0.000300 YES Maximum Displacement 0.000238 0.001800 YES RMS Displacement 0.000071 0.001200 YES
Low frequencies --- -6.8540 -6.6873 -6.2235 -0.0110 0.0556 0.1207 Low frequencies --- 289.2369 289.2482 403.8120
Optimised Borazine |
Comparison
Charge Distribution
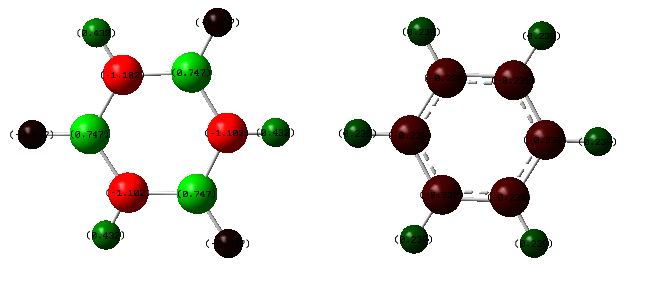
The first comparison between the two molecules is an NBO charge analysis. From the frequency calculated files of each molecule, the results are shown in the two tables below, as well as diagram that represents negative charge on the atoms with green representing positive charge and red negative charge. The magnitude of the charges are displayed by the brightness of the colour.
Charges on Benzene:
| Atom | NBO Charge |
| C | -0.239 |
| H | 0.239 |
Charges on Borazine:
| Atom | NBO Charge |
| N | -1.102 |
| B | 0.747 |
| H(-N) | 0.432 |
| H(-B) | -0.077 |
Since benzene is very symmetric and only composed of two different atoms, there are only two different charge values in the molecule. Since neither molecule has a formal charge, the charge densities in both add up to equal zero. Due to the electronegativity difference between B and N, both B, N and each 'type' of hydrogen (one bonded to B, one bonded to N) have different electronegativities. From the Pauling scale, boron has an electronegativity of 2.04, and nitrogen has one of 3.04.[1] This means that more electron charge is drawn towards the nitrogen as opposed to the boron, resulting in the charge on the nitrogen atoms being lower. Also because of the electronegativity difference, more of the electron density in the N-H bonds are further away from the hyrdogen giving it a more positive charge when attached to nitrogen as opposed to when attached to boron. It is clear from the diagram and these tables that there is strong ionic character in the B-N bonds of borazine that is not present in the C-C bonds of benzene.
Smf115 (talk) 23:54, 22 May 2018 (BST)Excellent charge analysis!
Molecular Orbitals
There are many similarities between the molecular orbitals of the two molecules which comes from them being isoelectronic. However, there are also differences that come from the altering charge distribution between the hetero atoms in borazine.
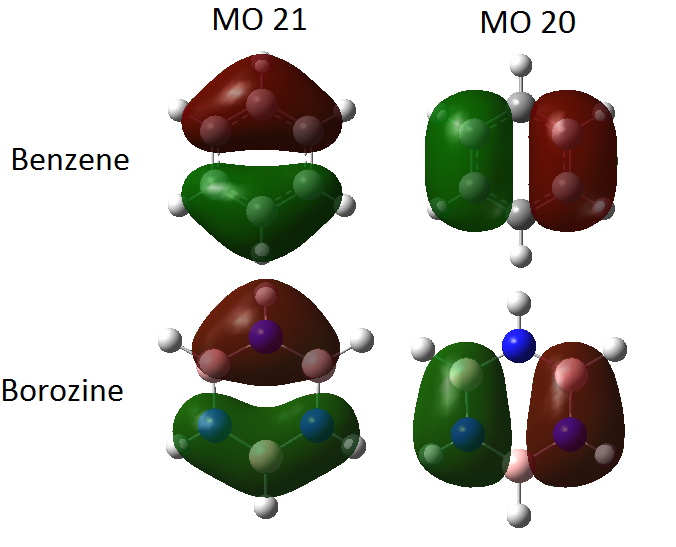
The degenerate MO pair, MO 20 and 21 which contains the HOMO are quite similar for both molecules. The diagram below shows these two MOs for each molecule. The HOMO (MO 21) shows π-bonding between the ring atoms with one nodal plane. In benzene the two lobes are symmetric, differing only in sign as the π-bond is equally distributed between the three carbon atoms. In borazine however, due to the higher electronegativity of nitrogen (over boron), the lobe containing two nitrogens has much more electron density around the nitrogen atoms. Because of this, the two lobes are antisymmetric, with the second lobe having most of its electron density at the centre where the nitrogen resides. The strength of the electron-drawing ability of nitrogen is shown with two of the boron atoms not even being fully covered by the π-bond. In the HOMO-1 orbitals (MO 20) the same symmetry is seen within the benzene molecule. This MO shows π-bonding between two sets of ring atoms, and sa expected, in borazine, most of the electron density between N and B in the π-bonds lies closer to the nitrogen atom. These orbitals are labelled as π3- π2 in both benzene and borazine. [2]
MO 13 in benzene and MO 16 in borazine show the σ-bonding between the ring atoms and the hydrogens. These MOs are shown below and as expected are all equal, whereas the B-H and N-H have different bonding orbital sizes due to their differences in electronegativity and thus bond lengths. The benzene orbital is characterised as b2u and the borazine one as a'2. </ref> [2]
The σ-framework between the ring atoms are shown by MO 14 for benzene and MO 15 for borazine. This MO appears the same for both molecules, showing that π-orbitals are more sensitive to the electron density of each atom than σ-orbitals. These are classified asb1u and a'2 for benzene and borazine respectively. [2]
Smf115 (talk) 00:06, 23 May 2018 (BST)Comparative MOs were selected and the mention of the symmetry of the orbitals and the electronegavity effects in borazine is really good. To improve, consider the images used as MO 21 has been positioned in a way which hides the pi-type orbitals (which should have a node in the plane of the molecule) leading to a few incorrect points in the analysis.
Aromaticity
After over a century of research, aromaticity has been given definitions and selection rules. In its simplest form, it is the additional stabilisation that certain (aromatic) molecules gain in comparison to simple π-conjugated molecules. A popular empirical rule set to determine if a molecule is aromatic are Hückel's Rules:
1. Must be planar. 2. Must have contiguous, cyclic array of p-orbitals perpendicular to plane of ring. 3. Must have (4n+2)p electrons.
This works well for many molecules and explains the aromaticity of borazine. In benzene, each carbon atom donates one p electron to the conjugated ring (n=1). However, in borazine nitrogen donates two electrons but boron does not donate any electrons to the conjugated system. This also results in six electrons in the conjugated ring (n=1) as the two molecules are isoelectronic.
These rules do not always apply though. At 20 K, benzene has been found to adopt a chair conformation whilst still exhibiting aromatic properties. [3]
One trait of aromatic orbitals that can be used as a test is the ring current that is generated from an applied magnetic field (current is induced in association with Ampere's Law - right hand rule) This is particularly useful in NMR and the ability to generate a ring current has been used as a definition for aromaticity. [4]
A major difference between aromatic compounds and simple π-conjuated compounds is that the carbon carbon bonds in are all the same length, which they are not if only in a conjugated system.
Smf115 (talk) 00:14, 23 May 2018 (BST)Overall a good report with an excellent charge analysis and good aromaticity discussion in the project section, however, consideration to the MOs just visualised would have improved the answer.
References
- ↑ J.E. Huheey, E.A. Keiter, and R.L. Keiter, Inorganic Chemistry : Principles of Structure and Reactivity, 4th edition, HarperCollins,1993.
- ↑ 2.0 2.1 2.2 N. D. Charistos, A. G. Papadopoulos, and M. P. Sigalas, J. Phys. Chem. A, 2014, 118, 1113-1122.
- ↑ M. Palusiak, and T. M. Krygowski, Cem. Eur. J.,2007, 13, 7996-8006.
- ↑ J. J. Engelberts, R. W. A. Havenith, and J. H. van Lenthe, Inorg. Chem. B,2005, 44, 5266-5272.