Rep:Mod:OPBIMM2

Part 1: Optimisation

NH₃

Molecule Name: Ammonia (NH₃)

Calculation Method: RB3LYP

Basis Set: 6-31G(d,p)

Final Energy E(RB3LYP): -56.55776873a.u.

RMS Gradient Norm: 0.00000485 a.u.

The Point Group: C_3v

Bond Length(N-H): 1.01798Å

Bond Angle(H-N-H): 105.74116°

As can be seen from the results above, all hydrogen atoms are in the same environment, hence they all have the same bond length and bond angle. From the C_3v point group we know it has a high degree of symmetry, so it is expected to have multiple bonds of the same type to be this symmetrical.

          Item               Value     Threshold  Converged?
 Maximum Force            0.000004     0.000450     YES
 RMS     Force            0.000004     0.000300     YES
 Maximum Displacement     0.000072     0.001800     YES
 RMS     Displacement     0.000035     0.001200     YES

Ammonia

The optimisation file for NH₃ can be found here.

Part 2: Vibrations and Charges

Figure 1: Display variations of an ammonia molecule in Gaussview.

Vibrations of NH₃

The NH₃ molecule consists of four atoms (one nitrogen and three hydrogens), thus using the '3N-6' rule there will be 6 modes of vibration. This is the same as displayed in Gaussview (see figure 1). All bends and stretches for this molecule are IR active due to them causing a change in dipole moment (selection rule: to be IR active a vibration should be accompanied by a change of dipole moment).

There are two degenerate sets of modes of vibration: 2 and 3 as well as 5 and 6. These are the scissoring bends and the asymmetric stretches. In each pair both vibrations display the same frequency , showing they have the same energy due to E=mc² & c= λν. Where 'λ' is wavelength and 'ν' is frequency.

Due to this, only four major peaks will be observed in the spectrum for gaseous ammonia.

Vibrations of NH₃

Frequency/ cm−1	Type of Vibration
1089.54	Wagging (Bending)
1693.95	Scissoring (Bending)
3461.29	Symmetric Stretching
3589.82	Asymmetric Stretching

Vibration '1' is the umbrella - it is a symmetric bend in which the three hydrogen atoms bend in unison replicating the folding in and out of an umbrella. This type of bending is commonly found in organic molecules in the form of an attached methyl group. The other symmetric vibration is number '4' from the list, this stretch is highly symmetric.

Figure 2: A Gaussview image of the charges within an ammonia molecule.

Charge distribution of NH₃

Nitrogen: -1.125, and each hydrogen: 0.375.

This adds up to make a total charge of 0, which is correct since the molecule isn't charged. The nitrogen has a negative charge due to being more electronegative than the hydrogen atoms. The electronegativity of nitrogen is 3.04, and for hydrogen it is 2.20. The hydrogen atoms must have a positive charge in order to reach a total charge throughout the molecule of zero. This is achieved by each hydrogen atom having a charge equal to the positive of the nitrogen charge divided by three (since there are three hydrogen atoms and one nitrogen atom).

Part 3: Reactions and Orbitals

N₂

Molecule Name: Nitrogen (N₂)

Calculation Method: RB3LYP

Basis Set: 6-31G(d,p)

Final Energy E(RB3LYP): -109.52412868 a.u.

RMS Gradient Norm: 0.00000060 a.u.

The Point Group: D_∞v

Bond Length (N≡N): 1.10550Å

Bond Angle (N≡N): 180°

        Item               Value     Threshold  Converged?
 Maximum Force            0.000001     0.000450     YES
 RMS     Force            0.000001     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000000     0.001200     YES

Nitrogen Molecule

Link to optimised Gaussian file for N₂: File

H₂

Molecule Name: Hydrogen (H₂)

Calculation Method: RB3LYP

Basis Set: 6-31G(d,p)

Final Energy E(RB3LYP): -1.17853936 a.u.

RMS Gradient Norm: 0.00000017 a.u.

The Point Group: D_∞v

Bond Length (H-H): 0.74279Å

Bond Angle (H-H): 180°

        Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000450     YES
 RMS     Force            0.000000     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000001     0.001200     YES

Hydrogen Molecule

Link to optimised Gaussian file for H₂: File

Vibrations of N₂ and H₂

Both molecules are linear so the number of vibrations they will have follows the '3N - 5' rule (specifically for linear molecules). This rule indicates both molecules will have one vibration, a stretching of the bond between the atoms.

Vibrations of N₂ & H

Molecule	Frequency/ cm−1	Type of Vibration
Nitrogen	2457.33	Stretching
Hydrogen	4465.68	Stretching

Figure 3: Windows from Gaussian showing the vibrational modes of Nitrogen (left) and Hydrogen (right) molecules.

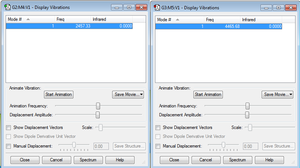
In both cases this stretch does not result in an IR reading as seen in the 'Display Vibrations' Gaussview picture on the right (but Ramon Scattering is observed). This is because they're both heterodiatomic molecules meaning the stretch does not result in a change in dipole moment (Infra-red spectroscopy selection rule: to be IR active a vibration should be accompanied by a change of dipole moment') thus are IR inactive.

$\tilde{\nu }=\frac{1}{2\pi c}\sqrt{\frac{k}{\mu }}$ (equation 1)

Where '$\tilde{\nu }$' is the wavenumber (cm^-1) which is the frequency of the peak divided by the speed of light, 'k' is the spring constant for the bond, 'c' is the speed of light, and 'μ' is the reduced mass of the system.

From 'equation 1' above we can see why N₂ has a lower frequency than H₂. The higher mass of the nitrogen molecule gives the system a higher reduced mass(μ) and because the frequency is proportional to the inverse of the root of the reduced mass, its frequency will be less. N₂ has a triple order bond stronger than the single order one of H₂. Because of this N₂ will have a higher spring constant. However, because the reduced mass of the nitrogen molecule (7m_p) is fourteen times as much as the hydrogen molecule (0.5m_p),the increase in 'k' for hydrogen will be smaller than the increase in 'μ'. Taking both conditions into consideration, for the nitrogen stretch the wavenumber and therefore frequency is lower than the one in hydrogen.

Charge Distribution of N₂ and H₂

Partial charge for each atom in both molecules is zero as neither are charged molecules and both atoms are the same. Because both atoms in each molecule are the same, there is no difference in electronegativity between them.

Haber-Bosch Process

N2 + 3H2 → 2NH3 (equation 2)

E(NH₃) = -56.55776873 a.u.

2*E(NH₃) = -113.11553746 a.u.

E(N₂) = -109.52412868 a.u.

E(H₂) = -1.17853936 a.u.

3*E(H₂) = -3.53561808 a.u.

ΔE = 2*E(NH₃)-[E(N₂)+3*E(H₂)] = -0.0557907 a.u. = -146.48kJ/mol

The energy change of this reaction has a negative sign because it is exothermic. This means that the products are more stable (lower in energy) than the reactants and energy is given out (lost to the environment) by the reaction.

Kimmo T. Klemola from Lappeenranta University of Technology gave an experimental calculated energy change (under standard conditions) of −91.88kJ/mol. This value is much less negative than ours showing the inaccuracy of the software in comparison to experimental data. These inaccuracies may have come from the approximation of the bond strengths of ammonia. In addition as this the Haber-Bosch process is done in different reaction conditions experimentally than are used in Gaussview.

Part 4 & 5: Formaldehyde

H₂CO

Molecule Name: Formaldehyde (H₂CO)

Calculation Method: RB3LYP

Basis Set: 6-31G(d,p)

Final Energy E(RB3LYP): -114.50319933 a.u.

RMS Gradient Norm: 0.00007386 a.u.

The Point Group: C_2v

Bond Length (C=O): 1.20676Å

Bond Length (C-H): 1.11057Å

Bond Angle (H-C=O): 122.39539°

Bond Angle (H-C-H): 115.21872°

From VSEPR we know the Carbon is sp² hybridised and has a distorted trigonal planar geometry. The bond angles are not the same (i.e. 120°). This is due to the distortion caused by the much higher electron density of the C=O double bond which repels the hydrogen atoms more, increasing the angle between the oxygen and each of the hydrogens and decreasing the angle between the hydrogens.

In formic acid (HCO₂) The bond angles are as followed:

Bond Angle (H-C=O): 123.94382°

Bond Angle (H-C-O): 113.46592°

Bond Angle (O-C=O): 122.59026°

This molecule still has a double bond and two single bonds attached to the central carbon, but with an oxygen(-hydrogen) replacing a hydrogen. The lack of symmetry in this molecule is shown by its point group: C₁. This causes even more distortion as now no two angles between each attached atom (or group) are the same (due to varying levels of repulsion from different electronic structures in each atom).

Item               Value     Threshold  Converged?
 Maximum Force            0.000197     0.000450     YES
 RMS     Force            0.000085     0.000300     YES
 Maximum Displacement     0.000270     0.001800     YES
 RMS     Displacement     0.000149     0.001200     YES

Formaldehyde Molecule

Optimised Gaussain file for H₂CO: Here

Vibrations of H₂CO

Figure 4: A Gaussview image of the IR spectrum for formaldehyde (top) and the NIST Chemistry WebBook IR spectrum for the same molecule (bottom).

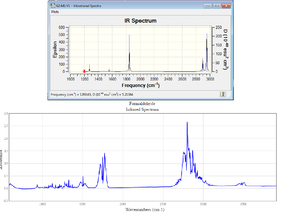
Using the '3N-6' rule for formaldehyde gives 6 modes of vibration.

Vibrations of H₂CO

Frequency/ cm−1	Type of Vibration
1200.65	Wagging (Bending)
1274.54	Scissoring (Bending)
1554.64	Symmetric Stretching (Bending)
1845.74	Asymmetric Stretching (C=O)
2897.28	Asymmetric Stretching (C-H)
2954.03	Asymmetric Stretching (C-H)

All of these vibrations are IR active (as they all induce a change in dipole moment). Since there are no degenerate vibrations, each vibrational mode creates a peak on the IR spectrum.

From 'figure 4' the Gaussview IR spectrum from H₂CO is close to the one published by the 'National Institute of Standards and Technology , with all of the major peaks being present in both. What can be seen is that the 'NIST' version has many other smaller value which will be due to overtones, isotopes and slightly different chemical environments in the solvent, all of which will lead to altering the frequency values.

Figure 5: A Gaussview image of the charges within formaldehyde (top) and formic acid (bottom).

Charge Distribution of H₂CO

Once again the molecule is not charged so all of the (internal) partial charges must add up to zero. Oxygen is the most electronegative atom in the system (3.44), so will have the most negative charge.

C: 0.221, H: 0.137 (both of them), O: -0.494.

In 'figure 5' the charges within the molecule of formic acid (HCO₂) are shown below formaldehyde. Here the charge on the carbon atom is even higher (0.637) due to there being another (electronegative) oxygen atom in the system requiring that the carbon be even more positively charged in order to give a total molecular charge of zero.

Synthesis of Formaldehyde by Dehydrogenation of Methanol

CH3OH ⇄ CH2O + H2 (equation 3)

E(CH₃OH): -115.72396437 a.u. [The optimised file of CH₃OH]

E(H₂CO): -114.50319933 a.u.

E(H₂): -1.17853936 a.u.

ΔE = [E(H₂CO) + E(H₂)] - E(CH₃OH): 0.04222568 a.u. = +110.86353129 kJ/mol

Figure 6: The energies of the lowest twelve molecular orbitals of formaldehyde from Gaussview.

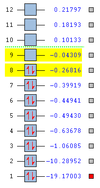
The experimentally determined value for this is +84 kJ/mol. Both the Gaussview calculated value and the experimental one for energy change are both positive, showing that this is an endothermic reaction that requires energy to be put in (the products are higher in energy in than the reactant).

Formaldehyde MOs

Figure 7: A Gaussview image of the first two molecular orbitals of formaldehyde. The first is on the left and the second on the right.

Figure 8: A Gaussview image of the third molecular orbital of formaldehyde.

Figure 9: A Gaussview image of the seventh molecular orbital of formaldehyde.

Figure 10: A Gaussview image of the HOMO and LUMO molecular orbitals of H₂CO.

For H₂ there are 8 filled molecular orbitals, and after this there are a more molecular orbitals that are unfilled. Within the first 8 MOs there are a variety of bonding and antibonding orbitals, some of which can be seen below.

The first two molecular orbitals are much lower in energy than the rest (as seen in figure 6). 'Figure 7' shows that they are both non-bonding core (filled) 1s orbitals, for oxygen and carbon. These orbitals will not contribute much if any to the chemical bond since there is no overlap between orbitals. The atomic orbitals must overlap in order to contribute to the bonding.

The third orbital is the (occupied) C-O σ bonding orbital. The electron density for this orbital is higher towards the oxygen. This is because the oxygen 2s orbital involved in the bonding is lower in energy (and closer to the C-O σ) than the carbon sp² that it is bonding to, so contributes more to the molecular orbital. This molecular orbital does contribute much more to the chemical bond than the last two but not as much as the π-bond.

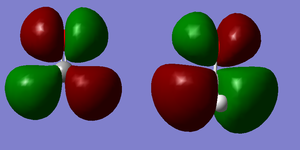
The π-bonding between the carbon and oxygen can be seen at the seventh molecular orbital (figure 9). Here there is a large overlap of the parallel half-filled p-orbitals from both oxygen and carbon forming a (C-O) π-bond perpendicular to the (C-O) σ-bond. This is even higher in energy (figure 6) and contributes greatly to the chemical bond.

The HOMO (highest occupied molecular orbital) is an anti-bonding orbital of an oxygen's p orbital and a CH orbital. The oxygen p orbital is in opposite phase to the CH bonding orbitals and is perpendicular to the π-bond (and the CH orbitals are in opposite phase to one another), so they do not overlap with one another. This is the seventh molecular orbital on the list (figure 6) and contributes to the antibonding of the chemical bond of the molecule. In both the HOMO molecular orbital, the lobes closest to the oxygen are smallest. This is because the carbon(hydrogen) orbitals are higher in energy than the degenerate p orbitals of oxygen, so are closer to the antibonding pair and thus contribute more towards it.

The LUMO (lowest unoccupied molecular orbital) is the eighth molecular orbital. This is an unoccupied (C-O) π* antibonding orbital formed from the p orbitals of oxygen and carbon being in opposite phases. Since CH₂ is higher in energy than the oxygen p orbital, it contributes more to this antibond as it is closer in energy to it. This is why the lobes around the CH₂ part of the molecule are larger. The fact that it is an antibonding orbital can be seen as it has nodes which illustrate zero overlap between lobes where no electron density is to be found.