Rep:Mod:OKD9643
Jake Hooton's Wiki
First Exercise With BH3
As per the instructions, a B3LYP optimisation was run with the 3-21g basis set on a molecule of BH3 set up with bond lengths of exactly 1.5 Å. A log file of the results is linked here: JH_bh3_opt_1st
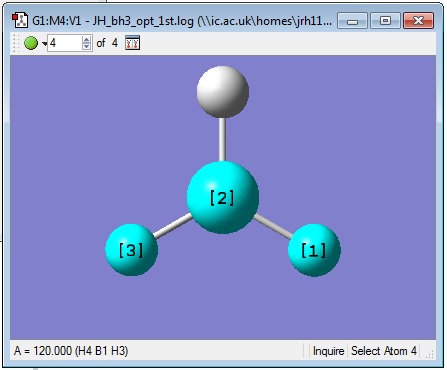
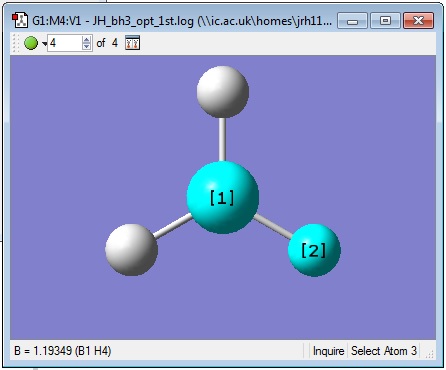
The inquisitor tool was used to find out some geometric information about the molecule. All bond angles were found to be 120.000° and all B-H bond lengths were found to be 1.19349 Å as shown in the pictures below.
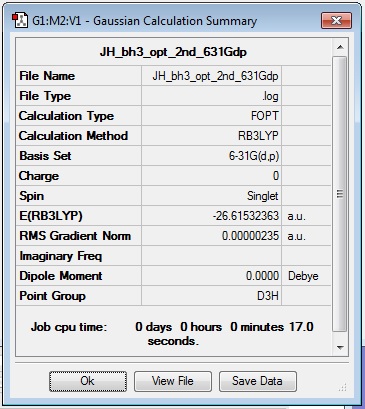
The results summary for the calculation is also presented in picture form below:
The item table is also provided:
Item Value Threshold Converged? Maximum Force 0.000413 0.000450 YES RMS Force 0.000271 0.000300 YES Maximum Displacement 0.001610 0.001800 YES RMS Displacement 0.001054 0.001200 YES Predicted change in Energy=-1.071764D-06 Optimization completed. -- Stationary point found.
Second Exercise With BH3
This time, a B3LYP optimisation was run with the improved 6-31G (d,p) basis set, on the molecule of BH3 pre-optimised with the 3-21G basis set. A log file of the results is linked here: JH_bh3_opt_2nd_631Gdp.
Geometric analysis with the inquisitor tool found that again, all bond angles were 120.000°, but each B-H bond length had shortened slightly to 1.19232 Å.
The results summary and item table are also provided below:
Item Value Threshold Converged? Maximum Force 0.000005 0.000450 YES RMS Force 0.000003 0.000300 YES Maximum Displacement 0.000019 0.001800 YES RMS Displacement 0.000012 0.001200 YES Predicted change in Energy=-1.305135D-10 Optimization completed. -- Stationary point found.
Notes on the Total Energies
The total energy for the BH3 calculation with the 3-21G basis set is -26.46226338 a.u.
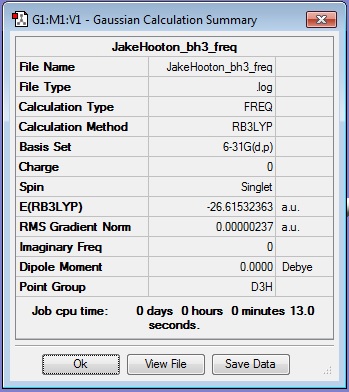
The total energy for the BH3 calculation with the 6-31G(d,p) basis set is -26.61532363 a.u.
Gallium Tribromide calculation
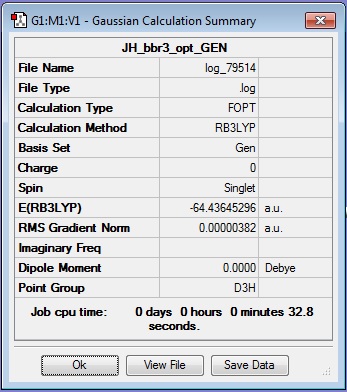
Results Summary:
Item table:
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000003 0.001800 YES RMS Displacement 0.000002 0.001200 YES Predicted change in Energy=-1.282693D-12 Optimization completed. -- Stationary point found.
Optimised Ga-Br bond length: 2.35018 Å
(found with the inquisitor tool)
N.B. - The literature value quoted in the CRC Handbook is 2.249 Å[1]. Therefore the computational result is approximately correct (certainly the right order of magnitude). The discrepancy in values will have arisen due to the use of a simple basis set in the Gaussian calculation, and simplifications in solving the Schroedinger equation.
Optimised Br-Ga-Br bond angle: 120.000° (found with the inquisitor tool)
Boron Tribromide Calculation
Results Summary:
Item Table:
Item Value Threshold Converged? Maximum Force 0.000008 0.000450 YES RMS Force 0.000005 0.000300 YES Maximum Displacement 0.000036 0.001800 YES RMS Displacement 0.000023 0.001200 YES Predicted change in Energy=-4.027605D-10 Optimization completed. -- Stationary point found.
Optimised B-Br bond length: 1.93396 Å (found with the inquisitor tool)
N.B. - The literature value quoted in the CRC Handbook is 1.893 Å [2]. Again, the computed value is approximately correct, showing a slight discrepancy due to the use of a simple basis set in the calculation, and simplifications in solving the Schroedinger equation.
Optimised Br-B-Br bond angle: 120.000° (found with the inquisitor tool)
Days 1 and 2 Analysis and Questions
| Compound | Bond | Bond Length / Ångstroms |
|---|---|---|
| BH3 | B-H | 1.19232 |
| BBr3 | B-Br | 1.93396 |
| GaBr3 | Ga-Br | 2.35018 |
The three above compounds are all trigonal planar compounds with the D3H point group and a group 13 atom as the central nucleus, therefore it is reasonable to compare these bond lengths. The initial, obvious trend is that with larger nuclei in the compound, the bond lengths are longer. The most basic explanation for this is that it has to be the case, in order to accommodate the greater covalent radius of the larger atoms. Substituting bromines for the hydrogens in such compounds makes a larger difference to the bond lengths (~0.8 Å) than does substituting gallium for boron as the central nucleus (~0.4 Å). This can be rationalised since again at a basic level, covalent radii are additive. Covalent radii generally increase down the periods of the periodic table due to electron shielding effects, and the difference in covalent radii is larger between hydrogen and bromine than it is between boron and gallium. This is because hydrogen is a period 1 element and bromine is period 4, and boron is a period 2 element while gallium is period 4.
Also, bromine is a very large atom compared with boron, so not only does its covalent radius have to be considered with respect to the central boron atom, it just about reaches the length at which it can cause steric interaction with a neighbouring bromine atom about the boron centre, perhaps causing it to sit at an energy minimum slightly further out from the central atom than expected. This could be another factor accounting for the large change between BH3 and BBr3 (~0.8 Å), however the effect would not be observed with GaBr3 since Ga is much larger central atom.
Gallium is a much larger atom than Boron, consequently its outermost filled atomic orbitals are larger and it will not form bonds so easily with small hydrogen atoms as it will with the larger bromine atoms (H and Br both act as one-electron donors). Hence, in the gas phase, GaH3 is unstable and does not exist, whereas BH3 does.
Bonds in Gaussview
We are told and can observe that in some structures, gaussview does not draw in bonds where we expect. In reality, there is no such thing as an 'absolute' localised bond between two atoms. Molecular orbital theory best rationalises structure of molecules, and this describes electrons sitting in MOs described by wavefunctions which cover the entire space of the molecule (and beyond!). It so happens that in almost every case, the sum of the probable electron density spread across the filled MOs of the molecule tends to show a build-up between the atoms in the place where we would normally draw a bond. The drawn bonds are imaginary, however they are a very useful, simpler model which give a quick and easy representation of the basic electronic structure of the molecule, allowing us to quickly draw some conclusions about its structure and reactivity. In addition, there will also be nodes or areas in the MOs with a very low probability for electron density. These correspond to areas between nuclei where we would not normally draw a bond in the displayed or skeletal structure.
The fact that Gaussview does not always draw in such bonds does not mean that it definitely does not exist - Gaussview simply has absolute distance criteria for each bond length, which it uses to decide whether or not a bond should be drawn. If atoms are positioned further apart than this length, then Gaussview will not draw a bond. In reality this does not mean that there is no interaction - there will be one - but we would also probably decide that it was too weak an interaction to define a proper 'bond'. The result though, in the abscence of other factors, will be that the atoms are drawn together, their interaction changes with respect to their separation, and wavefunction takes its form at a minimum where the shared electron density is definite enough for both us and Gaussview do decide to draw in a 'bond'.
Days 3 and 4
BH3 Frequency Calculation
Log file for the completed calculation: JakeHooton_bh3_freq
Results Summary:
Item Table:
Item Value Threshold Converged? Maximum Force 0.000005 0.000450 YES RMS Force 0.000002 0.000300 YES Maximum Displacement 0.000019 0.001800 YES RMS Displacement 0.000009 0.001200 YES Predicted change in Energy=-1.323376D-10 Optimization completed. -- Stationary point found.
Frequencies Table:
Low frequencies --- -0.9033 -0.7343 -0.0054 6.7375 12.2491 12.2824 Low frequencies --- 1163.0003 1213.1853 1213.1880
BH3 Frequency Calculation Repeated with Restricted Symmetry
Log file: JakeHooton_bh3_freq_restrictedsymmetry
Results Summary:
Item Table:
Item Value Threshold Converged? Maximum Force 0.000005 0.000450 YES RMS Force 0.000002 0.000300 YES Maximum Displacement 0.000019 0.001800 YES RMS Displacement 0.000009 0.001200 YES Predicted change in Energy=-1.324719D-10 Optimization completed. -- Stationary point found. GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Frequency Table
Low frequencies --- -0.9034 -0.7346 -0.0054 6.7355 12.2480 12.2812 Low frequencies --- 1163.0003 1213.1853 1213.1880
Vibrations
Continuing with the first one.
| Animation | Description | Frequency | Intensity (Infrared) | Symmetry D3H Point Group |
|---|---|---|---|---|
 |
Symmetric bending vibration, all three hydrogen nuclei oscillate out of the central plane together, and then back again in the other direction (wagging). The central boron nucleus rocks slightly about the centre of mass of the molecule to balance this. | 1163.00 | 92.5478 | A2" Only symmetric about principal Cn |
 |
A symmetric bending vibration whereby two of the hydrogen nuclei rock inwards together and outwards together in a scissoring action. The final B-H 'bond' remains essentially rigid, but these two B and H nuclei move back and forth about the centre of mass, counteracting the change in the 'scissoring' hydrogens. | 1213.19 | 14.0553 | E' Doubly degenerate and symmetric with respect to reflection plane perpendicular to Cn |
 |
An antisymmetric bending vibration where all hydrogen nuclei rock around the central boron nucleus, remaining in the same plane. The boron nucleus itself also moves slightly. One hydrogen, the 'top' one in the animation on the left, rocks towards one other hydrogen and away from the remaining hydrogen at any one time, whereas the other two hydrogens, at any one time, rock either towards or away from the first hydrogen, and in motion 'with' the other, final hydrogen. | 1213.19 | 14.0589 | E' Doubly degenerate and symmetric with respect to reflection plane perpendicular to Cn |
 |
A symmetric stretching vibration involving all three hydrogen nuclei moving inwards and outwards from the boron nucleus along the line of the original 'bonds', in a concerted fashion | 2582.26 | 0.0000 | A1' Totally Symmetric |
 |
An antisymmetric stretch involving two of the hydrogen nuclei stretching inwards and outwards from the centre of mass, with each with a mutually opposite motion at any one time (they are antisymmetric; this is very obvious when components are resolved). The central boron nucleus moves back and forth slightly to accommodate these changes and the third hydrogen nucleus is again essentially fixed. | 2715.43 | 126.3307 | E' Doubly degenerate and symmetric with respect to reflection plane perpendicular to Cn |
 |
A symmetric stretch where two of the hydrogen nuclei move inwards and outwards in a concerted fashion, whereas the third hydrogen nucleus moves inwards and outwards in an opposite fashion, at the same time. Again, the boron nucleus has to move very slightly to counter these changes about the centre of mass. | 2715.43 | 126.3211 | E' Doubly degenerate and symmetric with respect to reflection plane perpendicular to Cn |
The computed IR spectrum is presented below. It shows three peaks, despite the fact that there are six vibrations detailed above. The lack of one peak is clearly apparent - vibration number 4 in the above table has computed instensity of 0.000, therefore in practice it does not exist and therefore a peak will not show. Additionally, there are two pairs of degenerate vibrations (numbers 2 and 3, and 5 and 6. This means that each pair of vibrations will only produce one peak, since they occur at exactly the same energy/frequency. The presence of a third peak is due to the first vibration in the above table. It is different to the others and shows a peak at its own position with its own intensity value.
Gallium Tribromide Frequency Calculation
The completed calculation is published here on DSpace DOI:10042/25342 , and the log file is here JakeHooton_GaBr3_freq.log
Results Summary:
Item Table:
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000002 0.001800 YES RMS Displacement 0.000001 0.001200 YES Predicted change in Energy=-6.142862D-13 Optimization completed. -- Stationary point found.
Frequencies:
Low frequencies --- -0.5252 -0.5247 -0.0024 -0.0010 0.0235 1.2010 Low frequencies --- 76.3744 76.3753 99.6982
These values confirm that the original optimisation had converged at a minimum. The lowest "real" normal mode is the frequency at 76 cm-1, the doubly degenerate E' vibrations.
Gallium Tribromide Vibrations
When compared with the vibrations of BH3, there has been a re-ordering of the frequency of vibrations here. Of the first three vibrations (lowest frequency), the two degenerate E' vibrations and the A2" vibration have switched positions, so that in Gallium Tribromide the E' vibrations occur at a lower frequency, whereas in BH3 the A2" vibration occurred at the lower frequency. The final three vibrations (highest frequency) have remained in the same order.
| Animation | Description | Frequency | Intensity (Infrared) | Symmetry D3H Point Group |
|---|---|---|---|---|
 |
This vibration is directly comparable to the second bending vibration in BH3. It is a symmetric bending vibration, whereby two of the bromine nuclei rock inwards together and outwards together in a scissoring action. The final Ga-Br 'bond' remains essentially rigid; these two nuclei move back and forth together from the centre of mass, counteracting the motion of the 'scissoring' bromines. | 76.38 | 3.3447 | E' Doubly degenerate and symmetric with respect to reflection plane perpendicular to Cn |
 |
This is a degenerate vibration with the first one, and is directly comparable to the third bending vibration in BH3. It is an antisymmetric bending vibration where all bromine nuclei rock around the central gallium nucleus, remaining in the same plane. The gallium nucleus itself also moves slightly, which is a slight difference from the above vibration, despite the degeneracy. One bromine, the 'top' one in the animation on the left, rocks towards one other bromine and away from the remaining bromine at any one time, whereas the other two bromines, at any one time, rock either towards or away from the first bromine, and in motion 'with' the other, final bromine. | 76.37 | 3.3447 | E' Doubly degenerate and symmetric with respect to reflection plane perpendicular to Cn |
 |
The third vibration here is comparable to the first one of BH3, however it shows an important difference. It is again a symmetric bending vibration, however here, the primary nuclear movement appears to be the central (Gallium) nucleus. This rocks backwards and forwards about the centre of mass, with all three bromine nuclei rocking together to counter this motion, leaving their original plane, yet remaining co-planar as they do so. In BH3, the primary movement came from the surrounding hydrogen nuclei, with the central (boron) nucleus rocking as a counter-motion. | 99.70 | 9.2161 | A2" Only symmetric about principal Cn |
 |
A symmetric stretching vibration involving all three bromine nuclei moving inwards and outwards from the gallium nucleus along the line of their original 'bonds', in a concerted fashion. This is directly comparable to the fourth vibration mode of BH3. | 197.34 | 0.0000 | A1' Totally Symmetric |
 |
An antisymmetric stretch involving two of the bromine nuclei stretching inwards and outwards from the centre of mass, with each with a resolved component of motion that is mutually opposite at any one time (they are antisymmetric). The central gallium nucleus moves back and forth slightly to accommodate these changes and the third bromine nucleus is again essentially fixed. This vibration is directly comparable to the fifth vibration of the BH3 molecule. | 316.18 | 57.0704 | E' Doubly degenerate and symmetric with respect to reflection plane perpendicular to Cn |
 |
This vibration is comparable to the sixth vibration of the BH3 molecule, however this an important difference here too. The vibration is again a symmetric stretch, but the primary motion here is oscillation of the central gallium nucleus and one bromine nucleus (the 'top' one in the animation on the left), about the centre of their bond. The other two bromine nuclei do oscillate slightly, but to a much lesser extent. The BH3 molecule differed from this, since its central boron nucleus was virtually still in this vibration, and all three surrounding nuclei (hydrogens) were oscillating extensively. | 316.19 | 57.0746 | E' Doubly degenerate and symmetric with respect to reflection plane perpendicular to Cn |
The computed IR spectrum GaBr3 is also presented below.
| BH3 | GaBr3 |
|---|---|
| 1163.00 | 76.38 |
| 1213.19 | 76.37 |
| 1213.19 | 99.70 |
| 2582.26 | 197.34 |
| 2715.43 | 316.18 |
| 2715.43 | 316.19 |
Comments: The vibrational frequencies for the BH3 molecule are of the order of 10 times greater than the vibrational frequencies for GaBr3. A direct explanation for this comes from considering the equation ν = (1/2π) (k/μ)1/2, which shows that the wavenumber of vibration is inversely proportional to the square root of the reduced mass of the molecule. Since the BH3 structure is made up of much less massive atoms than the GaBr3 structure, its reduced mass will be much lower and hence its wavenumbers of vibrational excitation will be much higher. The results indicate that the B-H bonds are roughly 10 times stronger than the Ga-Br bonds, since they require more energy to excite the vibrational modes. Qualitatively, this could be rationalised by saying that Ga-Br forms weaker bonds since its constituent atoms are bigger and their valence orbitals will not overlap so well as those between B and H.
As mentioned above,there has been a re-ordering of the frequency of vibrations here. The two degenerate E' vibrations occur at a lower energy than the A2" vibration in GaBr3 whereas in BH3 the A2" vibration occurred at a lower frequency. The final three vibrations (highest frequency) have remained in the same order.
The computed spectra are similar in so far as they both show three peaks with the same pattern of occurrence at different frequencies. These peaks correspond to vibrations which are all to some degree comparable between the two molecules, due to their matching structures within the same point group. The peaks include two which are close together at low wavenumbers and one more peak occurring at a much higher wavenumber. The difference in energy of vibrations has been explained.
Important Notes: It is important to run the frequency calculations with exactly the same method and calculation details as were used for the optimisation of the molecules. This is because different basis sets will give optimisations based on separate potential energy curves when they are invoked for calculations. Running a vibrational analysis on a separate potential energy surface to that in which the molecules have been optimised to sit at a minimum is meaningless. This situation is comparable with real-world experiments - it is equivalent to holding all other variables steady when measuring the variance of one other particular variable when a change is invoked. If other variables had been allowed to change, the result would be meaningless.
The purpose of carrying out a frequency/vibrational analysis is to confirm that the optimisation has reached a minimum. The analysis essentially finds the derivative of the potential energy surface in which the molecule was optimised, and minimum points can be confirmed by observing the behaviour of this derivative. There is a short way to check the convergence by observing the log file for the frequency calculation - there are six low frequencies produced as an output. If these are all zero (generally within a small amount of tolerance) then the molecule has converged to a minimum. If one value is negative, then a transition state has been computed, and if more than one value is negative then the optimisation has not worked properly.
The six 'low frequencies' provided as an output in the log file simply represent numbers which can be checked to confirm an optimisation, as explained above. They stem from the fact that a non-linear molecule with N atoms has 3N-6 normal modes of vibration.
BH3 NBO Analysis
A qualitative MO diagram for BH3 is presented below, with pictures of the computed orbitals inserted for comparison:
Every single computed orbital provides a good match to the qualitatively drawn orbitals - they are always at least the same shape and show nodes in the correct places. This goes to show that qualitative molecular orbital theory is a very powerful tool for easily predicting the true molecular orbitals of molecules.
NH3 Work
The
nosymm
keyword was entered for these calculations.
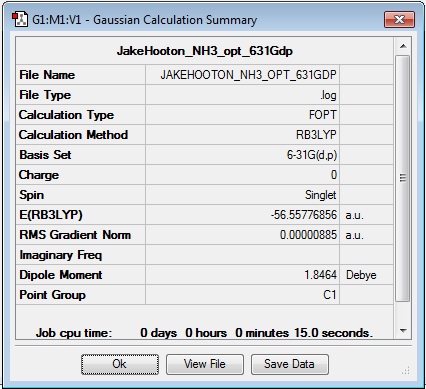
Optimisation
Log file: JakeHooton_NH3_opt_631Gdp
Results Summary:
Item table:
Item Value Threshold Converged? Maximum Force 0.000024 0.000450 YES RMS Force 0.000012 0.000300 YES Maximum Displacement 0.000079 0.001800 YES RMS Displacement 0.000053 0.001200 YES Predicted change in Energy=-1.629715D-09 Optimization completed. -- Stationary point found.
Bond lengths found to be 1.01797 Å, 1.01797 Å, and 1.01799 Å.
Bond angles found to be 105.741°, 105.749°, and 105.748°.
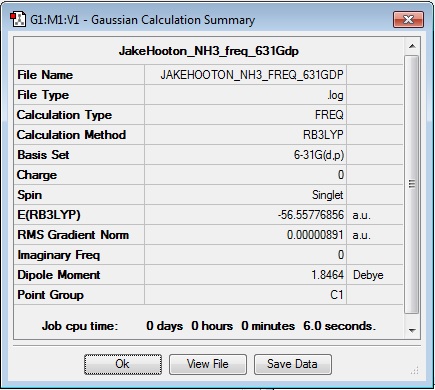
Frequency
Log file: JakeHooton_NH3_Freq_631Gdp
Results Summary:
Item table:
Item Value Threshold Converged? Maximum Force 0.000022 0.000450 YES RMS Force 0.000009 0.000300 YES Maximum Displacement 0.000078 0.001800 YES RMS Displacement 0.000039 0.001200 YES Predicted change in Energy=-1.621683D-09 Optimization completed. -- Stationary point found.
Low frequencies:
Low frequencies --- -30.7014 0.0000 0.0006 0.0014 20.2663 28.2997 Low frequencies --- 1089.5562 1694.1246 1694.1863
The low frequencies are not within the tolerated range of +/- 15, therefore the calculation must be repeated
Repeat of NH3 work
This time, the keywords
int=ultrafine pop=full scf=conver=9
were entered before the calculations were run, and
Full NBO
was selected under the NBO tab.
Optimisation Repeat
Log file:JakeHooton_NH3_opt_631Gdp_repeat.log
Results Summary:
Item Table:
Item Value Threshold Converged? Maximum Force 0.000002 0.000015 YES RMS Force 0.000001 0.000010 YES Maximum Displacement 0.000005 0.000060 YES RMS Displacement 0.000003 0.000040 YES Predicted change in Energy=-9.687887D-12 Optimization completed. -- Stationary point found.
Bond lengths found to be 1.01797 Å.
Bond angles found to be 105.744°, 105.744°, and 105.745°.
Frequency Repeat
Log file: JakeHooton_NH3_freq_631Gdp_repeat.log
Results Summary:
Item Table:
Item Value Threshold Converged? Maximum Force 0.000002 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000005 0.001800 YES RMS Displacement 0.000003 0.001200 YES Predicted change in Energy=-8.974384D-12 Optimization completed. -- Stationary point found.
Low Frequencies:
Low frequencies --- -6.8436 -5.1182 -1.4081 -0.0006 0.0003 0.0011 Low frequencies --- 1089.3464 1693.9250 1693.9291
These results are better and show that the calculation has worked.
NBO Analysis
The log file from the repeat optimisation was taken, and the charge distribution visualised across the atoms. This visualisation, and the charge range in a window to the left, are shown below:
The specific NBO charge numbers are also shown in the picture below:
Namely, the charges are -1.125 on N and +0.375 on each H.
H3N-BH3 Energy Calculation
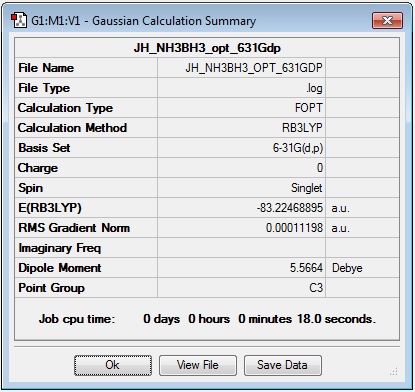
Optimisation
Log file: JH_NH3BH3_opt_631Gdp
Results Summary:
Item table:
Item Value Threshold Converged? Maximum Force 0.000234 0.000450 YES RMS Force 0.000083 0.000300 YES Maximum Displacement 0.000980 0.001800 YES RMS Displacement 0.000370 0.001200 YES Predicted change in Energy=-4.072051D-07 Optimization completed. -- Stationary point found.
Frequency
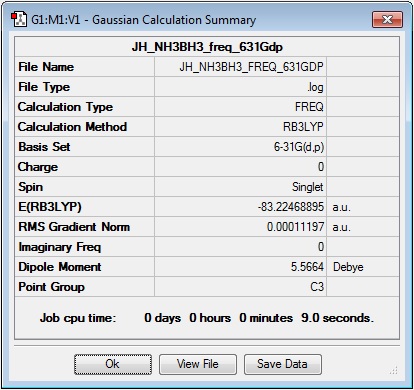
Log file: JH_NH3BH3_freq_631Gdp
Results Summary:
Item Table:
Item Value Threshold Converged? Maximum Force 0.000351 0.000450 YES RMS Force 0.000112 0.000300 YES Maximum Displacement 0.001349 0.001800 YES RMS Displacement 0.000452 0.001200 YES Predicted change in Energy=-5.257222D-07 Optimization completed. -- Stationary point found.
Low Frequencies:
Low frequencies --- -0.1770 -0.0270 -0.0050 12.1130 12.2132 37.7592 Low frequencies --- 264.5330 634.4432 639.1120
One of the low frequencies is reported as +38, this is clearly too high, so the calculation was repeated.
Repeat of H3N-BH3 Energy Calculation
This time, the keywords
opt=tight int=ultrafine
were entered before the calculations were run.
Optimisation Repeat
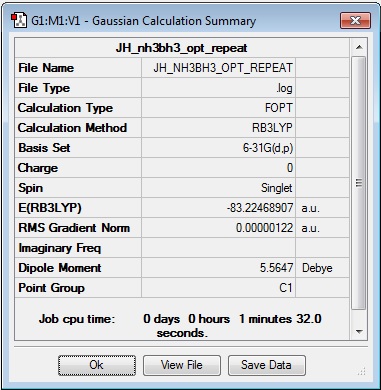
Log file: JH_NH3BH3_opt_repeat
Results Summary:
Item Table:
Item Value Threshold Converged? Maximum Force 0.000002 0.000015 YES RMS Force 0.000001 0.000010 YES Maximum Displacement 0.000027 0.000060 YES RMS Displacement 0.000009 0.000040 YES Predicted change in Energy=-9.032979D-11 Optimization completed. -- Stationary point found.
Frequency Repeat
Log file: JH_NH3BH3_freq_repeat
Results Summary:
Item Table:
Item Value Threshold Converged? Maximum Force 0.000005 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000027 0.001800 YES RMS Displacement 0.000010 0.001200 YES Predicted change in Energy=-1.202593D-10 Optimization completed. -- Stationary point found.
Low Frequencies:
Low frequencies --- -5.6787 0.0010 0.0011 0.0014 2.7389 4.2838 Low frequencies --- 263.4469 632.9666 638.4653
These low frequencies are all within the +/-15 range from 0, confirming that the optimization has reached a transition state.
Comparison
| Compound | Optimised Energy / au |
|---|---|
| BH3 | -26.61532363 |
| NH3 | -56.55776872 |
| H3N-BH3 | -83.22468907 |
| Difference | Energy / au | Energy / kJ mol-1 |
|---|---|---|
| ΔE=E(NH3BH3)-[E(NH3)+E(BH3)] | -0.05159672 | -135.467198679 |
This value represents the reaction energy of forming the adduct. The reverse of this process is the dissociation energy, which is therefore ~ +135 kJ mol-1.