Rep:Mod:OJA1811

Computational Labs: Module 1

Optimization

In this exercise BH₃, BBr₃ and GaBr₃ have been optimized with varying basis sets and pseudo potentials as appropriate. For each optimization a Summary Table and Item table is provided.

BH₃ 3-21G

For the first optimization of BH₃ the basis set 3-21G was used. This basis set is not very accurate and so the calculations only took 19 seconds to complete. A link to the log file can be found below. Media:OJABH3OPTIMISATION.LOG

Summary Table

BH3 Optimisation Summary
File Name	OJABH3OPTIMISATION
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	3-21G
Charge	0
Spin	Singlet
E(RB3LYP)	-26.46226338 a.u.
RMS Gradient Norm	0.00020672 a.u.
Imaginary Freq
Dipole Moment	0.0000 Debye
Point Group	D3H
Calculation Duration	19 seconds

Optimisation Calculations

 Item Value Threshold Converged?
 Maximum Force 0.000413 0.000450 YES
 RMS Force 0.000271 0.000300 YES
 Maximum Displacement 0.001610 0.001800 YES
 RMS Displacement 0.001054 0.001200 YES
 Predicted change in Energy=-1.071764D-06
 Optimization completed.
 -- Stationary point found.

Bond Information

BH3 Bond Information
B-H Bond Length	1.19Å
H-B-H Bond Angle	120.0°

Total Energy From the optimization using a 3-21G basis set was calculated at -26.46226338 a.u.

BH₃ 6-31G(d,p)

In this case BH₃ has been optimized again but with a more accurate basis set in order to obtain more reliable information on the bonds in the molecule. Media:OJABH3OPTIMISATION631GDP.LOG

Summary Table

BH3 Optimisation Summary
File Name	OJABH3OPTIMISATION631Gdp
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	0
Spin	Singlet
E(RB3LYP)	-26.61532252 a.u.
RMS Gradient Norm	0.00020672 a.u.
Imaginary Freq
Dipole Moment	0.0000 Debye
Point Group	D3H
Calculation Duration	1 minute 40 seconds

Optimisation Calculations

 Item Value Threshold Converged?
 Maximum Force 0.000433 0.000450 YES
 RMS Force 0.000284 0.000300 YES
 Maximum Displacement 0.001702 0.001800 YES
 RMS Displacement 0.001114 0.001200 YES
 Predicted change in Energy=-1.189019D-06
 Optimization completed.
 -- Stationary point found.

Bond Information

BH3 Bond Information
B-H Bond Length	1.19Å
H-B-H Bond Angle	120.0°

Total Energy From the optimization using a 6-31G(d,p) basis set was calculated at -26.61532252 a.u.

GaBr₃

DOI:10042/25206

Summary Table

GaBr3 Optimisation Summary
File Name	OJA_GABR3_OPT_OUTPUT
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	LANL2DZ
Charge	0
Spin	Singlet
E(RB3LYP)	-41.70082783 a.u.
RMS Gradient Norm	0.0000001620672 a.u.
Imaginary Freq
Dipole Moment	0.0000 Debye
Point Group	D3H
Calculation Duration	23 seconds

Optimisation Calculations

 Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000003 0.001800 YES
RMS Displacement 0.000002 0.001200 YES
Predicted change in Energy=-1.282678D-12
Optimization completed.
-- Stationary point found.

Bond Information

GaBr3 Bond Information
	Ga-Br Bond Length	Br-Ga-Br Bond Angle
Calculated	2.35 Å	120.0°
Literature	2.24 Å	123.1°

BBr₃

DOI:10042/25218

Summary Table

BBr3 Optimisation Summary
File Name	OJA_BBR3_OPT__GEN_OUTPUT_2
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	GEN
Charge	0
Spin	Singlet
E(RB3LYP)	-64.43645296 a.u.
RMS Gradient Norm	0.00000382 a.u.
Imaginary Freq
Dipole Moment	0.0000 Debye
Point Group	D3H
Calculation Duration	32.7 seconds

Optimisation Calculations

 Item Value Threshold Converged?
Maximum Force 0.000008 0.000450 YES
RMS Force 0.000005 0.000300 YES
Maximum Displacement 0.000036 0.001800 YES
RMS Displacement 0.000023 0.001200 YES
Predicted change in Energy=-4.026784D-10
Optimization completed.
-- Stationary point found.

Bond Information

BBr3 Bond Information
B-Br Bond Length	1.93 Å
Br-B-Br Bond Angle	120.0°

Analysis

Molecule	Calculated Bond Lengths	Predicted Bond Lengths
BH3	1.19 Å	1.16 Å
BBr3	1.93 Å	1.93 Å
GaBr3	2.35 Å	2.35 Å

The calculated bond lengths are in line with those predicted using the covalent radii of the atoms. There is a noticeable difference in BBr₃ however, and this may be due to the pi back donation from bromine into the empty p orbital of the boron causing the actual bond length to be shorter as there is a weak element of a double bond. This cannot occur with hydrogen as it has no other electrons to share, however as it is much smaller than bromine its orbitals are not diffuse so it can sit closer to the boron centre. There is a greater difference in electronegativity of B-Br than B-H indicating that B-Br will have a more polarized covalent bond than B-H. This in turn could result in the electron density not being held tightly between the two atoms so the bond is not as restricted, hence a longer bond in BBr₃.

Gallium is significantly bigger than Boron so a longer bond is expected for the obvious reason of the valence orbitals in gallium being far more diffuse than those of Boron. Despite the same number of valence electrons, Boron is a non metal and forms a covalent bond with Bromine and hydrogen where as gallium is a metal so its bond with Bromine is likely to be predominantly ionic. There will be a certain degree of repulsion between the two atoms and the longer bond length indicates that there will be a greater degree of repulsion between Ga and Br than B and Br.

Once GaBr₃ had been optimized Gaussview did not show the bonds between the atoms. This doesn't mean that the bond does not exist, rather that it exceeds Gaussview's predefined value of what a bond is. More loosely a bond can be described as what happens when two elements are effectively stuck to a shared electron density. This density may be spread unevenly between them, but the attraction to it is enough to keep the nuclei together and in the absence of other molecules, keeps the two elements together. On a basic level a bond can be seen to be the result of two individual atoms coming together and acting as a single body due to a force between them.

References

Frequency

As both the Ground state and the Transition state of a molecule have a 0 gradient along the potential energy curve it is important to determine whether the optimized geometries are ground states. In order to do this vibrational analysis is carried out on the molecules and the frequencies analysed. By doing this a second derivative is taken of the potential surface and if the molecule is in its ground state then all the frequencies calculated should be positive. This analysis has been carried out on BH₃ and GaBr₃. These calculations are also useful as the IR spectrum can be extracted and analysed, which can give important information about the molecules.

When carrying out a frequency analysis the basis set must be kept consistent with that of the optimization otherwise the system will not be appropriately optimized for the calculations. There are two types of "Low Frequencies" which have been included for both molecules. The first ones which are very small numbers are the -6 frequencies of the 3N-6 modes a molecule has and indicate the movement of the center of mass of the molecule. These are the small numbers which are very close to 0, indicating that the calculation is valid. The second set are the "real" frequencies of the molecule, and appear in the IR Spectrum.

For each frequency calculations a Summary table, "Low frequency" and Frequency table has been included. A comparison of the results can be found in the Analysis section.

BH₃

The molecule of BH3 that was optimised with a 6-31G(d,p) basis set was used in order to be as accurate as possible. A link to the full calculation file can be found here: Media:OJA_BH3_FREQ.LOG

Summary Table

BH3 Frequency Summary
File Name	OJA_BH3_FREQ
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	0
Spin	Singlet
E(RB3LYP)	-26.61532363 a.u.
RMS Gradient Norm	0.00000237 a.u.
Imaginary Freq	0
Dipole Moment	0.0000 Debye
Point Group	D3H
Time	47 seconds

Frequency Calculations

Low frequencies --- -0.9033 -0.7343 -0.0054 6.7375 12.2491 12.2824
Low frequencies --- 1163.0003 1213.1853 1213.1880

Vibrations

From the frequency calculations the IR-active vibrations can be deduced. A summary table below shows the movement of the molecule and its symmetry for each wavelength. By clicking on the thumbnail an animation will begin.

No.	Motion	Frequency (cm-1)	Intensity	Symmetry
1	All three Hydrogens wagging	1163	93	A2"
2	Two hydrogen's scissoring resulting in the remain H and B moving up and down in a concerted motion	1213	14	E'
3	All three hydrogen's rocking around central Boron	1213	14	E'
4	B-H bonds stretching out in a symmetric, concerted fashion	2582	0	A1'
5	Anti-symmetric stretching of two Hydrogen's	2715.43	126	E'
6	Two hydrogen's symmetrically stretching and one stretching asymmetrically	2715	126	E'

Spectrum

The IR spectrum of BH₃ can be seen below. Despite the fact that there are 6 separate vibrations there are only 3 peaks in the spectrum. There is no peak at 2582.26 due to its 0 intensity as the motion causes no change in dipole moment of the moelcule so is not IR active. For the E' symmetry motions the change in dipole moment will be very similar and as their intensities are so close no separation of the peaks can be seen.

IR Spectrum of BH₃

GaBr₃

The complete vibrational analysis calculation file for GaBr₃ can be found here: DOI:10042/25267

Summary Table

GaBr3 Frequency Summary
File Name	OJA_GABR3_FREQ_OUTPUT
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	LANL2DZ
Charge	0
Spin	Singlet
E(RB3LYP)	-41.70082783 a.u.
RMS Gradient Norm	0.00000011 a.u.
Imaginary Freq	0
Dipole Moment	0.0000 Debye
Point Group	D3H
Time	14 seconds

Frequency Calculations

Low frequencies --- -0.5252 -0.5247 -0.0024 -0.0010 0.0235 1.2010
Low frequencies --- 76.3744 76.3753 99.6982 

Vibrations

The frequencies and their intensities of the vibrations of GaBr₃ are tabulated below.

No.	Frequency (cm-1)	Intensity
1	76	3
2	76	3
3	100	9
4	197	0
5	316	57
6	316	57

Spectrum

The calculated IR spectrum of GaBr₃ can be found below. Again there are not 6 distinct peaks seen on this spectrum due to certain frequencies being almost identical and the lack of change in dipole moment leading to 0 intensity as it the vibration is not IR active.

IR Spectrum of GaBr₃

Analysis

Comparison table of BH₃ and GaBr₃

BH3			GaBr3
Frequency (cm-1)	Intensity	Symmetry	Frequency (cm-1)	Intensity	Symmetry
1163	93	A2"	76	3	E'
1213	14	E'	76	3	E'
1213	14	E'	100	9	A2"
2582	0	A1'	197	0	A1'
2715	126	E'	316	57	E'
2715	126	E'	316	57	E'

Overall GaBr₃ frequencies are lower than BH₃ frequencies. This is due to Energy (E) being inversely proportional to wavelength (λ), and the wave number (v) being the reciprocal of wavelength meaning that E ∝ v. Complimenting the bond length information derived from the earlier optimization calculations, the IR proves that BH₃ bonds are far stronger than GaBr₃ bonds. This is related to their relative bond lengths with B-H bonds being considerably shorter than Ga-Br bonds. Shorter bond lengths result in stronger bonds as the electrons are held closely to both nuclei so they experience greater attraction from the nuclei resulting in more energy being needed to overcome this attraction. In GaBr₃ bonds the electrons are more diffuse from the two nuclei so less energy is required to break the bond.

Despite the molecules having the same geometry there has been a reordering of modes which can be clearly seen when comparing the IR frequencies. The two E' bond bending modes are lower in energy than the A2" bond bend in GaBr₃ which is the reverse for BH₃. In both cases the A2" and E' modes and the A1' and E' modes lie close together but are separating by a significant amount. This is because the lower frequencies are bond bending movements whereas the high frequencies are bond stretching. Bending bonds requires less energy than stretching as it is the angles between the atoms which are distorted whereas bond stretching involves the extension and compression of bonds.

Molecular Orbitals

To determine the molecular orbitals of a molecule the promised file is taken and an energy calculation is carried out. These orbitals can then be compared to the approximated ones too see how accurate a qualitative Molecular Orbital diagram is. In this example the Molecular orbitals of BH₃ have been calculated and compared to the ones predicted by employing MO theory.

BH₃

The complete energy calculation file for BH₃ can be found here: DOI:10042/25323

Diagram

Below the MO diagram for BH₃ is shown, with images of the calculated MOs being displayed next to the predicted ones. The biggest difference is the consistency between filled and unfilled orbitals, depending on the LCAOs the green can be either filled or unfilled. The general form of the calculated orbitals matches the predicted ones, and identifying which orbitals correlated wasn't difficult indicating that using MO theory is a useful qualitative method in the absence of computational analysis. However if accurate information or further calculations were to be conducted it would be advisable to use the computational method in order to avoid an increase in error. An interesting point to note would be the order of the 3a'₁and 2e' orbitals. In the predicted model there is ambiguity about the ordering of these two orbitals however the calculations conducted confirm the order of these two orbitals with 3a'₁ is placed below the 2e' as shown below.

alt text

NBO Analysis

In order to evaluate the Natural bond orbitals an optimization and vibrational analysis of the molecule must first be carried out in order to establish it is in it's ground state configuration. Then the charge distribution of the molecule can be reviewed. For this exercise NH₃ has been used.

NH₃

Optimisation Calculation: Media:OJA_NH3_OPT_631GDP_5.LOG

Optimisation Summary Table

NH3 Optimisation Summary
File Name	OJA_NH3_OPT_631GDP_5
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	0
Spin	Singlet
E(RB3LYP)	-56.55776863 a.u.
RMS Gradient Norm	0.00000279 a.u.
Imaginary Freq
Dipole Moment	1.8464 Debye
Point Group	C3V
Calculation Duration	1 minute 15 seconds

Calculations

 Item Value Threshold Converged?
Maximum Force 0.000005 0.000450 YES
RMS Force 0.000003 0.000300 YES
Maximum Displacement 0.000010 0.001800 YES
RMS Displacement 0.000007 0.001200 YES
Predicted change in Energy=-7.830149D-11
Optimization completed.
-- Stationary point found. 

Frequency Calculation: Media:OJA_NH3_FREQ_5.LOG

Frequency Summary

NH3 Frequency Summary
File Name	OJA_NH3_FREQ_5
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	0
Spin	Singlet
E(RB3LYP)	-56.55776856 a.u.
RMS Gradient Norm	0.00000279 a.u.
Imaginary Freq	0
Dipole Moment	1.8464 Debye
Point Group	C3
Time	41 seconds

Frequency Calculations

Low frequencies --- -11.6527 -11.6490 -0.0045 0.0333 0.1312 25.5724
Low frequencies --- 1089.6616 1694.1736 1694.1736 

As discussed in the earlier Frequency section, the first 6 low frequencies should be close to 0 to prove the validity of the calculation. However in this calculation one of the frequencies is unusually high, at ~25cm^-1, giving slight cause for concern. On review of the .log file related to this it was found that all forces were converged and very close to 0 therefore the calculation was successful. In order to minimize this frequency a more accurate basis set or method would be required but for the purpose of this exercise it is not appropriate to investigate that here.

Molecualr Orbitals

Energy Calculation: DOI:10042/25321

Charge Distribution

Charge distribution across NH₃

Using NBO analysis the charge distribution of NH3 can be viewed through a colour coded representaiton. Green indicates poisitive charge and red indicates negative charge; as expcected the central nitrgoen is hgihly negatively charged. The charge limits in the case are from -1.125 to +1.125. Below the actual charges of the atoms has been tabulated. Hydrogen is very slightly positively charged, hence its green colouring in the adjacent image.

Atom	Charge
N	-1.125
H	+0.375

Reaction Energies

Accumulating the skills learned from the above exercises in optimization, vibrational analysis, molecular orbitals and NBO Analysis, the reaction energies for the formation of NH₃BH₃ can be calculated. By using the optimization energies the dative N-B bond energy can be found and then with comparison to the separate NH₃ and BH₃ energies the association/dissociation bond energy can be found.

NH₃BH₃

Optimisation: Media:OJA_NH3BH3_OPT_631GDP.LOG

Summary Table

NH3BH3 Optimisation Summary
File Name	OJA_NH3BH3_OPT_631GDP
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	0
Spin	Singlet
E(RB3LYP)	-83.22469007 a.u.
RMS Gradient Norm	0.00006839 a.u.
Imaginary Freq
Dipole Moment	5.5653 Debye
Point Group	C1
Calculation Duration	3 minutes 7 seconds

Calculations

 Item Value Threshold Converged?
 Maximum Force 0.000139 0.000450 YES
 RMS Force 0.000063 0.000300 YES
 Maximum Displacement 0.000771 0.001800 YES
 RMS Displacement 0.000338 0.001200 YES
 Predicted change in Energy=-2.028055D-07
 Optimization completed.
 -- Stationary point found.

Frequency: Media:OJA_NH3BH3_FREQ.LOG

Summary Table

NH3BH3 Frequency Summary
File Name	OJA_NH3BH3_FREQ
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	0
Spin	Singlet
E(RB3LYP)	-83.22469000 a.u.
RMS Gradient Norm	0.00006830 a.u.
Imaginary Freq	0
Dipole Moment	5.5653 Debye
Point Group	C1
Time	1 minute 22 seconds

Calculations

Low frequencies --- -0.0015 -0.0010 -0.0007 18.9885 23.6408 42.9617
 Low frequencies --- 266.5827 632.3776 639.4313 

Dissociation Energy

Enery Table

Molecule	Energy
NH3	-56.56 a.u.
BH3	-26.61 a.u.
NH3BH3	-83.22 a.u.

In order to find the bond energy and hence the dissociation energy of NH₃BH₃, the relative energies of the molecuels were taken from the calculaitons conducted and used in the following equation. Calculation ΔE=E(NH3BH3)-[E(NH3)+E(BH3)] = -83.22 - (-26.61 + -56.56) = -0.05a.u. = -0.05*2625.50 kj/mol = -131.275kj/mol

The bond dissociation energy of NH₃BH₃ has been determined to be -131.28 kjmol^-1. In comparison with a literature value found at 30.7 kcal/mol (128.45kj/mol) this method of determining bond dissociation energies can be taken to be successful.

References

Computational Labs: Module 2

D-Space Links

caption

Calculation	Benzene	Boratabenzene	Pyridinium	Borazine
Optimisation	DOI:10042/25676	DOI:10042/25669	DOI:10042/25667	DOI:10042/25672
Frequency	DOI:10042/25675	DOI:10042/25666	DOI:10042/25665	DOI:10042/25671
Energy	DOI:10042/25673	DOI:10042/25668	DOI:10042/25664	DOI:10042/25670

Optimisation

Summary Table

caption

Optimization	Benzene	Boratabenzene	Pyridinium	Borazine
File Name	OJA_BENZ_OPT_631GDP_OUTPUT	OJA_BORAT_OPT_631GDP_OUTPUT	OJA_PYR_OPT_631GDP_OUTPUT	OJA_BORZ_OPT_631GDP_OUTPUT
File Type	.log	.log	.log	.log
Calculation Type	FOPT	FOPT	FOPT	FOPT
Calculation Method	RB3LYP	RB3LYP	RB3LYP	RB3LYP
Basis Set	6-31G(d,p)	6-31G(d,p)	6-31G(d,p)	6-31G(d,p)
Charge	0	-1	1	0
Spin	Singlet	Singlet	Singlet	Singlet
E(RB3LYP)	-232.25820551 a.u.	-219.02052984 a.u.	-248.66807396 a.u.	-242.68458739 a.u.
RMS Gradient Norm	0.00009550 a.u.	0.00015822 a.u.	0.00003896 a.u.	0.00006610 a.u.
Imaginary Frequency
Dipole Moment	0.0001 Debye	2.8465 Debye	1.8727 Debye	0.0002 Debye
Point Group	C1	C1	C1	C1
Time	1 minute 13.8 seconds	2 minutes 52.9 seconds	2 minutes 54.5 seconds	3 minutes 28.2 seconds

Item Table

Benzene

 Item Value Threshold Converged?
Maximum Force 0.000212 0.000450 YES
RMS Force 0.000085 0.000300 YES
Maximum Displacement 0.000991 0.001800 YES
RMS Displacement 0.000315 0.001200 YES
Predicted change in Energy=-5.157444D-07
Optimization completed.
-- Stationary point found. 

Boratabenzene

 Item Value Threshold Converged?
Maximum Force 0.000159 0.000450 YES
RMS Force 0.000069 0.000300 YES
Maximum Displacement 0.000911 0.001800 YES
RMS Displacement 0.000335 0.001200 YES
Predicted change in Energy=-6.630189D-07
Optimization completed.
-- Stationary point found. 

Pyridinium

 Item Value Threshold Converged?
Maximum Force 0.000064 0.000450 YES
RMS Force 0.000023 0.000300 YES
Maximum Displacement 0.000702 0.001800 YES
RMS Displacement 0.000174 0.001200 YES
Predicted change in Energy=-6.897601D-08
Optimization completed.
-- Stationary point found. 

Borazine

 Item Value Threshold Converged?
Maximum Force 0.000093 0.000450 YES
RMS Force 0.000033 0.000300 YES
Maximum Displacement 0.000338 0.001800 YES
RMS Displacement 0.000096 0.001200 YES
Predicted change in Energy=-1.027046D-07
Optimization completed.
-- Stationary point found. 

Frequency

Summary Table

caption

Optimization	Benzene	Boratabenzene	Pyridinium	Borazine
File Name	OJA_BENZ_FREQ_OUTPUT	OJA_BORAT_FREQ_OUTPUT	OJA_PYR_FREQ_OUTPUT	OJA_BORZ_FREQ_OUTPUT
File Type	.log	.log	.log	.log
Calculation Type	FREQ	FREQ	FREQ	FREQ
Calculation Method	RB3LYP	RB3LYP	RB3LYP	RB3LYP
Basis Set	6-31G(d,p)	6-31G(d,p)	6-31G(d,p)	6-31G(d,p)
Charge	0	-1	1	0
Spin	Singlet	Singlet	Singlet	Singlet
E(RB3LYP)	-232.25820586 a.u.	-219.02052984 a.u.	-248.66807396 a.u.	-242.68458753 a.u.
RMS Gradient Norm	0.00009558 a.u.	0.00015830 a.u.	0.00003894 a.u.	0.00006600 a.u.
Imaginary Frequency
Dipole Moment	0.0001 Debye	2.8465 Debye	1.8727 Debye	0.0002 Debye
Point Group	C1	C1	C1	C1
Time	4 minutes 15.7 seconds	5 minutes 0.4 seconds	4 minutes 22.8 seconds	5 minutes 7.5 seconds

Low Frequencies

Benzene

 Low frequencies --- -17.0537 -14.3774 -9.3919 -0.0009 -0.0006 0.0003
Low frequencies --- 413.7989 414.4772 620.8619 

Boratabenzene

 Low frequencies --- -13.1241 0.0008 0.0009 0.0009 15.0608 18.1734
Low frequencies --- 371.3450 404.2340 565.2523 

Pyridinium

 Low frequencies --- -7.2019 -0.0005 0.0002 0.0006 17.3427 18.5430
Low frequencies --- 392.4561 404.0619 620.4714 

Borazine

 Low frequencies --- -17.0998 -10.8330 -5.8654 0.0006 0.0013 0.0013
Low frequencies --- 288.8425 289.6877 404.1663 

NBO Analysis

Table showing Charge distributions

Benzene	Boratabenzene	Pyridinium	Borazine
Range: -0.239 - +0.239	Range: -0.588 - +0.588	Range: -0.483 - +0.483	Range: -1.102 - +1.102

Table showing charge distribution values. Atoms are numbered with the top atom being 1 and then in a clockwise fashion around the ring

Atom	Benzene	Boratabenzene	Pyridinium	Borazine
1	-0.239	0.202	-0.476	0.747
2	-0.239	-0.588	0.071	-1.102
3	-0.239	-0.250	-0.241	0.747
4	-0.239	-0.340	-0.122	-1.102
5	-0.239	-0.250	-0.241	0.747
6	-0.239	-0.588	0.071	-1.102
H-1	0.239	-0.096	0.483	-0.077
H-2	0.239	0.184	0.285	0.432
H-3	0.239	0.179	0.297	-0.077
H-4	0.239	0.186	0.292	0.432
H-5	0.239	0.179	0.297	-0.077
H-6	0.239	0.184	0.285	0.432

Table showing electronegativity values on the Pauling Scale

Atom	Electronegativity
C	2.550
H	2.200
N	3.040
B	2.040

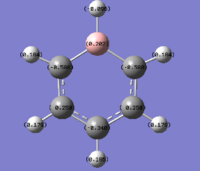
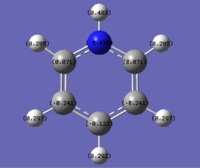
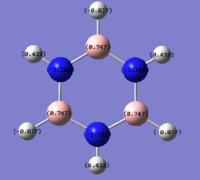
As can be seen from the images above, changing a single atom in the ring affects all other atoms in it. In benzene there is a uniform spread of electrons across the carbons as they are all the same. However in Boratabenzene the introduction of an electropositive boron causes the neighboring carbons to have an increase in electron density making them more negative and hence a bright red colour. The carbon opposite the boron shows higher electronegativities than those next to it, indicating at an uneven spread of electrons over the remaining carbon atoms.

The opposite of this can be seen in pyridinium. Here an electronegative atom has been introduced into the ring and that means that the electron density is drawn towards it, making the neighboring carbons far more electropositive than in benzene. This then leads to a build up of electron density on atoms 3 and 5 leaving atom 4 (opposite the nitrogen) more electropositive than carbon 4 in benzene.

The expected trend of distinct electropositive and electronegative sites is seen in Borazine. Due to the difference in electronegativities of boron and nitrogen, as seen in the table below, the electron density is held in a repeat pattern and is not smeared across the ring as seen in boratabenzene and pyridinium.

The changing electronegativities of the atoms in the ring has an effect on the charge distribution on the Hydrogen atoms. The more electronegative a ring atom is the more electron density that the nitrogen holds. This means that the phenomena seen on the ring atoms is the inverted pattern seen on the hydrogens.

References

MO Diagram of Benzene

Using the molecular orbitals of Benzene acquired through calculations an MO diagram with accompanying LCAOs has been constructed. The molecular orbitals calculated have been interpreted in order to form the LCAOS by using known information about the molecule, e.g. that the carbons are sp² hybridized due to the planar nature of the molecule.

These MOs can be used to show that benzene is aromatic. For example the pi orbital arrangement of orbitals shows how the electrons can be delocalized around the ring as there are no breaks in the orbital. This can also be seen in the sigma orbitals as the orbitals can be seen to not be localized on to specific atoms but instead extend across the ring, indicating that the molecule is aromatic.

In order for a molecule to be aromatic it must hold 4n+2 electrons in it's pi orbitals. Benzene fulfills this brief and can be seen on the MO diagram. The 3 bonding pi orbitals hold two electrons each leading to 6 electrons in total. In this case n=1, and benzene fulfills the criteria to be aromatic.

MO Diagram of Benzene

MO comparison

Below is a comparison table of 3 of the molecular orbitals from Benzene, Boratabenzene, Pyridinium and Borazine.

Orbital	Benzene	Boratabenzene	Pyridinium	Borazine
12	E=-0.518	E=-0.289	E=-0.790	E=-0.525
	Due to the LCAOs all being the same size and shape in Benzene there is through space bonding which forms a ring around and inside the molecule. This is formed from the sp2 C orbitals and the s Hydrogen orbitals. IN Boratabenzene however, there is no contribution from Boron and a ring isn't formed due to a mismatch in orbital sizing causing poor through space bonding. Pyridinium differs in that a great proportion of the orbital is sat at the electronegative nitrogen and is obviously contributing greatly to this MO. It indicates that this MO is built from 4 carbon sp2 opposite one another which then mathces the symmetry of the Nitrogen sp2 orbital. In Borazine it would appear that it is predominatantly s orbitals of hydrogen and boron that are forming this molecular orbtial and nitrogen is not interacting as such. this may be due to a lack of symmetry match between the arrangement of boron-hydrogen orbitals with nitrogen ones. For Benzene, Boratabernzene and Pyridinium this orbital shows no degeneracy, however in borazine it does, indicating that there is a differing in ordering of the borazine MOs in comparison to Benzene.
14	E=-0.439	E=-0.204	E=-0.700	E=-0.434
	Orbital 14 in benzene can be seen to be made up of a crown of alternating Carbon sp2 orbitals with no contribution from the Hydrogen s orbitals. This differs greatly from the other three which all show interaction between the ring atoms and outer Hydrogen s orbitals to a certain degree, showing that different LCAOs are interacting in these species. Boratabenzene shows the interaction between two hydrogen s orbitals with two carbon sp2 orbitals, and then down the middle of the molecule the orbitals are inverted and mirrored. There is no contribution form the boron in this orbital and it lacks the same uniformity as the benzene orbital. In pyridinium there is predominantly an interaction between the carbon and hydrogen orbitals leading to through space bonding in the centre of the molecule however it doesn't appear that the nitrogen is contributing in this one either. Due to the complimentary orbital sizes in borazine there is a lot of through space bonding resulting in the double horseshoe formation at the top and middle of the molecule. In borazine this MO shows degeneracy with orbital 13 showing that the ordering of the orbitals has been changed which could be due to the presence of nitrogen, a common factor of the two molecules.
20	E=-0.247	E=-0.035	E=-0.508	E=-0.276
	This orbital is constructed from the pz orbitals and provides the delocalised pi ring which makes benzene aromatic. Boratabenzene and pyridinium show opposing variations on the 'original' benzene orbital, boratabenzene loses the electron density over the boron and carbon-4 whereas in pyridinium the electron density is drawn away from carbon 2 and 6 due to its high electronegativity. This leads to an asymmetrical distribution of electrons across these two molecules. As expected the borazine orbital size and shape is most similar to the benzene orbital however slightly distorted due to the changing in electronegativity of Nitrogen and Boron.

By changing the certain atoms in a molecule the whole MO set will be affected, firstly in the relative energies of the orbital levels. A general trend can be seen throughout this set of molecules:

Boratabenzene < Benzene ~ Borazine < Pyridinium

This reflects the electronic structure of each of the complexes. Pyridinium carries a positive charge so is lacking in electrons and hence the whole molecule is higher in energy in comparison to the other three. Conversely Boratabenzene carries a negative charge making it lower in energy as it is electron rich. Benzene and borazine are neutral and are most similar in electron density distribution and so are close in energy.

The ordering of the MOs is also affected which includes where degenerate orbitals sit. As the symmetry of the LCAOS for the ring atoms will change due to the introduction of new atoms so will their energy levels, which results in the order being slightly different for each molecule. Below the ordering and energies of orbitals 7 to 27 can be seen, with degenerate orbitals highlighted in red.

Both pyridinium and Borazine have no degenerate molecular orbitals and this is due to a lack of symmetry in the molecule. When either N or B is replaces a Carbon in the benzene ring the orbital's eigen values change resulting in different energies for the orbitals.