Rep:Mod:NishMeisterMod3

Nisha Mistry

Module 3: Characterising Transition Structures

The aim of this module was to characterise transition structures on potential energy surfaces for the Cope Rearrangement and the Diels Alder cycloaddition. We are going to use molecular orbital-based methods, numerically solve the Schrodinger equation and locate transition structures based on the local shape of the potential energy surface.

The Cope Rearrangement

1,5-hexadiene under goes a [3,3]-sigmatropic shift known as the Cope Rearrangement. The mechanism is thought to be a concerted pericyclic reaction which goes via a chair or boat transition structure. The reaction is under thermodynamic control and is reversible. An equilibrium is established between the two conformers and overall, there is no change in total bond energy. The scheme for this reaction, drawn using ChemDraw Pro, is shown below in figure 1.

Figure 1: The Cope Rearrangement of 1,5-hexadiene

Optimisation of the Reactants and Products

A molecule of 1,5-hexadiene was drawn in Gaussian with an "anti" linkage for the 4 central atoms, the structure was cleaned and then optimised using the Hartree-Fock method and the 3-21G basis set. Table 1 shows the structure, symmetry and energy of the molecule.

Another molecule of 1,5-hexadiene was drawn in Gaussian, this time with a "gauche" linkage across the 4 central carbons. The structure was optimised using the HF/3-21G method and basis set. The structure, symmetry and energy is shown below in table 1. The "gauche" conformer was expected to be higher in energy than the "anti" conformer, and this is indeed what was seen in the calculations.

A series of conformers were drawn and optimised, including the C_i anti 2 conformer, to try to find the lowest energy conformer of 1,5-hexadiene. The conformers, the symmetries and energies are all shown below in table 1.

The energies in the table exactly match those found on the Module 3 wiki page in appendix 1.

Conformer	Structure	Point Group	Energy (Hartrees) HF/3-21G	Relative energy (kcal mol-1)
anti 1	DOI:10042/to-11054	C2	-231.69260	0.04
anti 2	DOI:10042/to-11055	Ci	-231.69254	0.08
anti 3	DOI:10042/to-11059	C1	-231.69097	1.06
anti 4	DOI:10042/to-11061	C2h	-231.68907	2.25
gauche 1	DOI:10042/to-11062	C2	-231.69167	0.62
gauche 2	DOI:10042/to-11063	C1	-231.68962	1.91
gauche 3	DOI:10042/to-11065	C2	-231.68772	3.10
gauche 4	DOI:10042/to-11064	C1	-231.69266	0.0
gauche 5	DOI:10042/to-11067	C1	-231.68916	2.20
gauche 6	DOI:10042/to-11068	C2	-231.69153	0.71

Table 1: A table to show the different conformers, symmetries and energies of 1,5-hexadinene

It was found that the two lowest energy conformers were anti 1 and gauche 4 where anti 1 was only 0.04 kcal mol^-1 higher in energy that gauche 4. Using this method of optimisation, the lowest energy conformer was found to be gauche 4 because of an attractive interaction present between the π orbital and the vinyl proton.

The anti 1, anti 2 and gauche 4 conformers have been optimised again, this time using the DFT method and B3LYP/6-31G(d) basis set, this is a higher basis set and therefore would be expected to give more reliable results. Table 2 shows the 3 conformers after they have been optimised with the new method and basis set and the relative energies.

Conformer	Structure	Point Group	Energy (Hartrees) HF/3-21G	Energy (Hartrees) B3LYP/6-31G	Relative Energy (kcal mol-1)
anti 1	DOI:10042/to-11052	C2	-231.69260	-234.61180	0.0
anti 2	DOI:10042/to-11056	Ci	-231.69254	-234.61171	0.06
gauche 4	DOI:10042/to-11066	C1	-231.69266	-234.61133	0.29

Table 2: A table to show the change in energy on optimising with a more accurate basis set

It can be seen that after optimising with the higher basis set, B3LYP/6-31G(d), the geometries of the molecules showed some changes, the point groups however did not change from C₂, C_i and C₁. This new basis set shows that the anti 1 conformer is now the most stable conformer and is 0.06 kcal mol^-1 more stable than the anti 2 conformer and 0.29 kcal mol^-1 more stable than the gauche 4 conformer. The gauche conformer becomes less stable because the C-C-C bond angle increases from 111.87° to 113.47°, which increases the distance between the π orbital and the vinyl proton, so decreasing the attractive interactions in this conformer. Table 3 below shows the changes in bond lengths and angles.

Basis Set	HF/3-21G					B3LYP/6-31G
	Bond lengths (Å)			Bond angles (°)		Bond lengths (Å)			Bond angles (°)
Conformer	C=C	=C-C-	C-C	C=C-C	C-C-C	C=C	=C-C-	C-C	C=C-C	C-C-C
anti 1	1.32	1.51	1.55	124.75	111.37	1.33	1.50	1.55	125.24	112.67
anti 2	1.32	1.51	1.55	124.82	111.35	1.33	1.50	1.55	125.29	112.68
gauche 4	1.32	1.51	1.55	125.02	111.87	1.33	1.50	1.55	125.48	113.47

Table 3: A table to show the changes in bond lengths and bond angles on using a higher basis set for optimisation

On optimising with a higher level basis set it can be seen that overall, the geometry changes very little. The bond lengths get closer to the ideal bond lengths of 1.34 Å, 1.50 Å, 1.55 Å for the C=C, =C-C-, and C-C lengths respectively. There are also very small increases in the bond angles.

Frequency Calculations

To compare the energy values for the three conformers above to experimental values, further calculations are required. Providing there are no negative frequencies, frequency calculations also confirm that a true minimum energy has been reached.

Frequency calculations on the anti 1, anti 2 and gauche 4 conformers were run through Gaussian. The lowest real frequencies have been tabulated below, showing that the conformers are a true minimum. The Jmols and IR spectrum of the 3 conformers are also shown in table 4.

Conformer	Lowest Real Frequency (cm-1)	IR Spectrum
	74.97	DOI:10042/to-11053
	74.29	DOI:10042/to-11070
	75.00	DOI:10042/to-11071

Table 4: A table to show the low frequencies of the 3 conformers

The most intense frequencies on the spectra for the anti 1 and anti 2 conformers appear at 939 cm^-1 and are a result of the 4 alkene protons (-CH=CH₂) bending. On the spectrum for the gauche 4 conformer, the most intense frequency also appears at 939 cm^-1 but it is less intense because only 2 of the alkene protons are bending, and not all 4 as in the 2 anti conformers. The high frequency (3000 - 3500 cm^-1) peaks have also decreased in intensity in the gauche spectrum compared to the spectra for the anti conformers. These peaks correspond to various alkene stretches and bends and since, in the gauche conformer, some of the symmetry is lost compared to the anti conformers, there are an increase in the number of peaks in this region, but they are all of lower intensity.

In the log files of the frequency calculation there is data on the thermochemistry of the conformers. The sum of the electronic and zero-point energies is the potential energy at 0K including the zero-point vibrational energy. The sum of the electronic and thermal energies is the energy at 298.15 K and 1 atm pressure, and includes contributions from the translational, rotational and vibrational energy modes at this temperature. The sum of the electronic and thermal enthalpies contains an additional correction for RT (H = E + RT) which is important when looking at dissociation reactions. Finally the sum of the electronic and thermal free energies includes the entropic contribution for the free energy. The four energies for each conformer are shown below in table 4.

Temperature	0 K	298.15 K			0 K
Conformer	Sum of electronic and zero-point energies (hartrees)	Sum of electronic and thermal energies (hartrees)	Sum of electronic and thermal enthalpies (hartrees)	Sum of electronic and thermal free energies (hartrees)	Sum of electronic and zero-point energies (hartrees)	Sum of electronic and thermal energies (hartrees)	Sum of electronic and thermal enthalpies (hartrees)	Sum of electronic and thermal free energies (hartrees)	DOI
anti 1	-234.46929	-234.46197	-234.46102	-234.50016	-234.46885	-234.46885	-234.46885	-234.46885	DOI:10042/to-11302
anti 2	-234.46920	-234.46186	-234.46091	-234.50078	-234.46877	-234.46877	-234.46877	-234.46877	DOI:10042/to-11301
gauche 4	-234.46869	-234.46146	-234.46052	-234.50011	-234.46826	-234.46826	-234.46826	-234.46826	DOI:10042/to-11309

Table 5: A table to show the thermochemistry of the 3 conformers

It can be seen that as more contributions, such as vibrations and rotations, and corrections such as RT and entropic contributions are added to the potential energy, the increases as a more accurate value for the energy is obtained. The calculations were run again, at 0 K. The Sum of electronic and zero-point energies ought to have been the same however this calculations was carried out using the "Freq=ReadIsotopes" option in Gaussian and the isotopes used were carbon 12.0 and hydrogen 1.0, and not the average of all isotopes, hence the difference in energy. At 0K it can be seen that all 4 energies are identical, this shows that at this temperature there are no thermal contributions and therefore no rotations or translations.

Optimising the 'Chair' and 'Boat' Transition Structures

Chair

An allyl fragment was first optimised using the HF/3-21G method and basis set, this was then copied twice into a new window, and positioned to look like the chair transition state. The Hartree Fock method and 3-21G basis set has been used to optimise the chair transition state, using the "Optimisation to a TS (Berny)" option in Gaussian. The keywords "Opt=NoEigen" were used to stop the calculation failing is the true transition state was not found. The optimised molecule is shown below.

Figure 2: Optimised chair transition state using HF/3-21G (TS Berny) DOI:10042/to-11193

For the chair transition state, the frequency calculation gave one imaginary frequency of 818 cm^-1, showing that it had been successfully optimised. If it had be found that there was more than one imaginary frequency then it would have been known that the fully optimised transition state had not be found. The vibration resulting in the imaginary frequency was seen to be the one corresponding to the Cope Rearrangement and is shown below.

Figure 3: Vibration showing the Cope rearrangement

The transition state was optimised again using the frozen coordinate method and specifying the frozen bond lengths to be 2.2 Å. After this, the bond breaking/forming distances were also optimised. The two structures are shown below.

Figure 4: Optimised chair transition state using the frozen coordinate method DOI:10042/to-11194

Figure 5: Optimised bond breaking/forming distances DOI:10042/to-11418

The distance between the terminal bonds, which are the bond forming and bond breaking lengths, and the bond angles, in the two optimised structures are shown in the table below. It can be seen that both the methods give identical bond lengths and bond angles.

Method	HF/3-21G		Frozen Coordinate		Optimised bond breaking/forming distances
Bond lengths (Å)	2.02	2.02	2.2	2.2	2.02	2.02
C-C-C bond angle (°)	120.5	120.5	122.0	122.0	120.5	120.5

Table 6: A table to show the bond forming/bond breaking lengths

Boat

The boat transition structure has been optimised using the QST2 method. In this method, the reactants and products are specified so that the calculation can interpolate between them to find the transition state. The anti 2 conformer, with C_i symmetry, was used as the reactant and product and the molecules were relabeled to correspond to each other in the following way:

Figure 6: Labeling on the reactant and the product DOI:10042/to-11195

The QST2 transition state optimisation calculation failed almost immediately, because the calculation does not consider the possibility of rotation around the central bonds. The geometries were modified to more closely resemble the boat transition structure. For the reactant, the C2-C3-C4-C5 dihedral angle was changed to 0°, and the C2-C3-C4 and C3-C4-C5 angles were changed to 100°. For the product the C2-C1-C6-C5 dihedral angle was changed to 0° and the C2-C1-C6, and C1-C6-C5 angles were changed to 100°. They now looked like the following:

Figure 7: Modified structures of the reactant and product

Figure 8: Optimisation which gave a twist boat structure DOI:10042/to-11196

This result gave a twist boat structure (figure 8) so the the calculation was run again, this time choosing to calculate the force constants once. The structure obtained from this optimisation was a boat and is shown below in figure 9.

Figure 9: Optimisation which gave a boat transition structure DOI:10042/to-11197

There is only one imaginary frequency at 840 cm^-1, and it corresponds to the bond breaking/bond forming vibration as shown in figure 10.

Figure 10: Vibration showing the bond breaking and bond forming

IRC Calculations

From the optimised chair and boat transition states it is almost impossible to predict which conformers the transition states will lead to. However on Gaussian it is possible to predict which structure it will lead to by following the minimum energy pathway from the transition state to the local minimum. This is called the Intrinsic Reaction Coordinate method.

In Gaussian, IRC was chosen as the job type and as the reaction coordinate is symmetrical, it was computed in the forward direction only, and the force constant was calculated once at the beginning. 50 points along the IRC were considered.

For the chair transition state the output showed that calculation had not yet reached the minimum energy. Three different methods were tried to attempt to reach the true minimum geometry, there were: (i) the last point from the IRC was taken and a normal minimisation run (ii) the IRC was restarted using a larger number of points (iii) the IRC was rerun specifying that force constants were to be run at every step.

The results from the initial IRC calculation and the three modified methods to reach the true minimum are shown in the table below.

Method	Initial IRC	IRC + normal minimisation	IRC + a larger number of points	IRC + force constants at every step
Geometry	not a true minimum DOI:10042/to-11200	gauche 1 DOI:10042/to-11199	not a true minimum DOI:10042/to-11203	gauche 1 DOI:10042/to-11204
Energy (hartrees)	-231.68704	-231.69167	-231.68704	-231.69166

Table 7: A table to show structures obtained from the IRC calculations of the chair transition state and the modifications in order to find the true minimum geometry

From this table it can be seen that 2 of the methods give a minimum conformation. These methods are (i) (taking the last point from the initial IRC and running a normal minimisation) and (iii) (redoing the IRC, specifying for the force constants to be computed at every step). The minimum conformer obtained was the gauche 1 conformer which had an energy of -231.69167 hartrees.

The reaction path for this calculation is shown below, and shows that the structure obtained from the initial IRC calculation is almost a minimum since the gradient obtained is extremely close to zero.

Figure 10: Graphs to show the energy and gradient along the reaction path from the chair transition state

For the IRC calculations of the boat transition state the energy and reaction path as shown in figure 11 showed that the structure had not been minimised to the true minimum. The same three methods as above were also applied to the boat transition state and the results of each calculation are shown in the table below.

Method	Initial IRC	IRC + normal minimisation	IRC + a larger number of points	IRC + force constants at every step
Geometry	not a true minimum DOI:10042/to-11206	gauche 4 DOI:10042/to-11209	not a true minimum DOI:10042/to-11210	not a true minimum DOI:10042/to-11211
Energy (hartrees)	-231.67839	-231.69266	-231.67839	-231.68672

Table 8: A table to show structures obtained from the IRC calculations of the boat transition state and the modifications in order to find the true minimum geometry

Figure 11: Graphs to show the energy and gradient along the reaction path from the boat transition state

The table shows that method (i) has minimised the boat transition state to the gauche 4 conformer. As shown in tables 1 and 2, the gauche 4 conformer is one of the lowest energy conformer showing that reactions that proceed via the boat transition state result in the lower energy conformer.

Calculating Activation Energies

In order to calculate activation energies for the reactions via both transition states the chair and boat transition structures were minimised using the B3LYP/6-31G(d) method and basis set.

Method	HF/3-21G				B3LYP/6-31G(d)
	Jmols	Electronic Energy	Sum of electronic and zero-point energies	sum of electronic and thermal energies	Jmols	Electronic Energy	Sum of electronic and zero-point energies	sum of electronic and thermal energies
			0 K	298.15 K			0 K	298.15 K
Reactant - anti 2		-231.69254	-231.53954	-231.53257		-234.611710	-234.46920	-234.46186
Chair Transition State		-231.61932	-231.46670	-231.46134		-234.55698	-234.41493	-234.40901
Boat Transition State		-231.60280	-231.45093	-231.44530		-234.54309	-234.40234	-234.39601

Table 9: A table to show the energies of the structures minimised with both basis sets

From these energies, it is possible to calculate the activation energies. By minusing the Sum of electronic and zero-point energies of the reactant from each of the transition states, it is possible to obtain the activation energy at 0 K. Carrying out these calculations using the sum of electronic and thermal energies gives the activation energies at 298.25 K

Method	HF/3-21G		B3LYP/6-31G(d)		Experimental
	0 K	298.15 K	0 K	298.15 K	0 K
ΔE chair (kcal/mol)	45.71	44.70	34.05	33.16	33.5 ± 0.5
ΔE boat (kcal/mol)	55.60	51.23	41.96	41.32	44.7 ± 2.0

Table 10: A table to show the activation energies of the reaction via the chair and boat transition states

These activation energies show that the energies obtained by using the higher basis set, B3LYP/6-31G, show a much better correlation to values obtained by experimental methods. The chair transition state is lower in energy but leads to the higher energy product. This means that this is the kinetically favourable reaction route, where gauche 1 is the kinetic product. The boat transition state is higher is energy but leads to a lower energy conformer. This means that the reaction via the boat transition state is the thermodynamically favourable route and that gauche 4 is the thermodynamic product. Since there is free rotation around the central C-C bond, the overall product of the reaction is likely to be the anti 2 conformer. With further study into the energy barrier for rotation, i.e. looking at the eclipsed conformers, it would be possible to tell how much energy this would require.

The Diels Alder Cycloaddition

The Diels Alder reaction [4+2]-cycloaddition of a conjugated diene and a dieneophile. It is a pericyclic reaction in which the π orbitals of the dienophile are used to form new σ bonds with the π orbitals of the diene. Substituted dieneophiles can stabilise the transition state of this reaction and effect regioselectivity.

Formation of cyclohexene

The reaction between ethylene and butadiene is a concerted [4+2] reaction is is considered to be Diels Alder reaction.The reaction scheme and curly arrows for this reaction has been drawn in ChemDraw Pro and is shown below in figure 12.

Figure 12: The Diels Alder reaction of cis-butadiene and ethene

The structures of ethylene and cis-butadiene were drawn on Gaussian and optimised using the AM1 semi-empirical molecular orbital method. The HOMO and LUMO of the two moelcules, along with their symmetries, are shown in table 11.

	cis-butadiene DOI:10042/to-11328		ethylene DOI:10042/to-11327
Orbital	Structure	Symmetry	Structure	Symmetry
HOMO		anti-symmetric		symmetric
LUMO		symmetric		anti-symmetric

Table 11: A table to show the HOMO and LUMO of cis-butadiene

The transition state for this reaction was drawn in Gaussian and optimised using the AM1 semi-empirical molecular orbital method. The frozen coordinate method was first used, setting the new C-C bonds to 2.2Å. The structure from this optimisation is shown below.

Figure 13:The transition state for the Diels Alder reaction after optimisation using the frozen coordinate method DOI:10042/to-11321

These bond lengths were then optimised, and the structure obtained is shown in the table below with the geometry data.

Structure		Figure 14:The transition state for the Diels Alder reaction after optimisation to a transition state DOI:10042/to-11326
Energy (hartrees)		0.11166
bond lengths (Å)	New C-C	2.12
	C-C	1.40
	C=C	1.38

Table 12: A table to show structure and geometry data of the transition state

Typical sp³ and sp² carbon bond lengths are 1.55 Å, and 1.34 Å respectively. The bond lengths obtained from this optimisation show that in the transition state, the double bonds are increasing in length as they increasingly gain single bond character, and the single bond that was in butadiene is shorter than the average C-C single bond as its double bond character increases. The new C-C bond lengths are much longer than the typical C-C bond length. The van der Waals radius for a carbon atom is 1.7 Å. This indicates that, at the transition state, the carbon atoms are within the required distance for a bond to begin to form.

The vibrational analysis confirmed that the structure was a transition state by the presence of an imaginary vibration. This vibration appeared at 956 cm^-1 and corresponds to the reaction path at the transition state. The formation of the two bonds is synchronous, which agrees with the experimental data as the reaction is known to be concerted. The vibration is shown in figure 15.

Figure 15: The vibration showing the formation of cyclohexene

The lowest real vibration is asynchronous, and had a frequency of 147 cm^-1. The vibration is shown below in figure 16.

Figure 16: The vibration showing the formation of cyclohexene

Table 13 shows the HOMO and LUMO of the transition state. By comparing these orbitals to the ones shown in table 11 it can be seen that the HOMO of cis-butadiene combines with the LUMO of ethylene and that both of these orbitals are anti-symmetric, which results in the anti-symmetric HOMO for the transition state. The symmetric LUMO of the transition state is the result of the combination between the LUMO of cis-butadiene and the HOMO of ethylene. An allowed reaction is one in which the HOMO of one reactant can interact with the LUMO of the other reactant and the reaction occurs in a stereospecific concerted fashion. This reaction which fulfills both criteria, as can be seen from the orbital overlap, including the appropriate symmetries of the HOMOs and LUMOs, and the imaginary vibration showing the synchronous formation of the two new bonds, is therefore allowed.

Orbital		Symmetry
HOMO		anti-symmetric
LUMO		symmetric

Table 13: A table to show the HOMO and LUMO of the transition state

The product molecule was also optimised using the AM1 semi-empirical molecular orbital method and had an energy of -10.16 kcal mol^-1. The structure is shown below in figure 17.

Figure 17:DOI:10042/to-11370

In conclusion, the AM1 semi-empirical molecular orbital method is a suitable method for determining the molecular orbitals of the two reactants and looking at the overlap of these orbitals at the transition state. The vibrations agree with the theory that the reaction would be allowed and would proceed in a concerted fashion.

Studying the Regioselectivity of the Diels Alder Reaction

The regioselectivity of the Diels Alder reaction can be shown in the reaction of cyclohexa-1,3-diene with maleic anhydride. The reaction is known to give two products, the exo product is the thermodynamic product and the eno is the kinetic product. The following calculations and discussion of orbital overlap and geometries show this. Figure 18, drawn in ChemDraw Pro, shows the reaction scheme and the exo and endo products.

Figure 18:Reaction between cyclohexa-1, 3-diene and maleic anhydride

Cyclohexandiene and maleic anhydride were drawn in Gaussian and their structures optimised using the AM1 semi-empirical molecular orbital method. Table 14 shows the HOMO and LUMO of the two reactants along with the symmetry of the orbitals.

	Cyclohexadiene DOI:10042/to-11329		Maleic Anhydride DOI:10042/to-11330
Orbital	Structure	Symmetry	Structure	Symmetry
HOMO		anti-symmetric		symmetric
LUMO		symmetric		anti-symmetric

Table 14: A table to show the HOMO and LUMO of cyclohexadiene and maleic anhydride

The optimised reactants were used to draw a guess structure for the transition state. This was then optimised to a transition state (Berny) using Gaussian by first using the frozen coordinate method and freezing the bond forming lengths to be 2.2 Å. The structures obtained from this optimisation are shown in table 15. The energies from this optimisation show that the endo product is more stable by 0.87 kcal mol^-1.

	Exo	Endo
Structure	DOI:10042/to-11335	DOI:10042/to-11336
Energy (kcal mol-1)	-32.00	-32.87

Table 15: A table to show the structures and energies of the exo and endo Diels Alder transition states after optimisation using the frozen coordinate method

The bond forming lengths were then optimised giving the following structures, energies and molecular orbitals.

		Exo	Endo
Structure		DOI:10042/to-11338	DOI:10042/to-11339
Jmols
Energy (kcal mol-1)		-31.64	-32.32
Molecular Orbitals	HOMO
	LUMO

Table 16: A table to show the the exo and endo Diels Alder transition states after optimising to the transition state

This table shows that the endo conformer is now only 0.68 kcal mol^-1 more stable than the exo conformer. The HOMO of the exo transition state is made up of the HOMO of the cyclohexadiene and the LUMO of the maleic anhydride, both of which are anti-symmetric. The HOMO orbital of the endo transition state results from the combination of the same orbitals but from the opposite face of one of the molecules, allowing there to still be the appropriate overlap of the orbitals in the correct phase. For the same reasons as above, this reaction is therefore allowed.

The main structural difference between the endo and exo forms is the directions in which the maleic anhydride faces. In the exo form the maleic anhydride oxygens face towards the bridge-head, and in the endo form, the maleic anhydride oxygens point away from the bridge-head. For this reason the exo form is likely to be more strained as there would be steric effects from the bridge-head. This can be shown by carbon carbon distances between the carbonyl carbons in maleic anhydride and either the CH₂-CH₂ bridging carbons for the exo product or the CH=CH bridging carbons for the endo product. These lengths were 2.95 Å and 2.89 Å respectively which show that in fact the carbons are closer together in the endo conformer. However there are extra hydrogens in the exo product which point towards the anhydride group. This would create more steric repulsion. Steric effects are not included in the Gaussian calculations.

By an examination of the nodal planes in the HOMOs of the two transition states, it can be seen that there would be a secondary orbital overlap effect in the endo transition state where there would not be any effect in the transition state of the exo form. This secondary orbital overlap occurs the oxygen atoms on the maleic anhydride and the π orbital of the C=C bonds in cyclohexadiene and can be seen in the table above.

The vibrations in table 17 show two different vibrational frequencies. The imaginary frequency shows the reaction paths of the reactions and it can be seen that the formation of the new bonds are synchronous. The lowest real frequencies are asynchronous.

Frequency	Exo	Endo
Imaginary frequency (cm-1)
	-813.12	-806.24
Lowest Real Frequency (cm-1)
	59.97	62.58

Table 17: A table to show the vibrations of the exo and endo Diels Alder transition states

IRC Calculations

For the optimised transition structures IRC calculations were carried out to show the minimum energy pathway from the reactants to the products via the transition states. As above, IRC was chosen as the job type in Gaussian, and since this time, the reaction coordinate is not symmetrical, it was computed in both directions with force constants calculated at every step. 100 points along the reaction coordinate were considered.

	Exo	Endo
Structure after Intial IRC calculation	fully optimised DOI:10042/to-11393	fully optimised DOI:10042/to-11396
Energy (kcal mol-1)	-100.36	-100.51
Reaction Path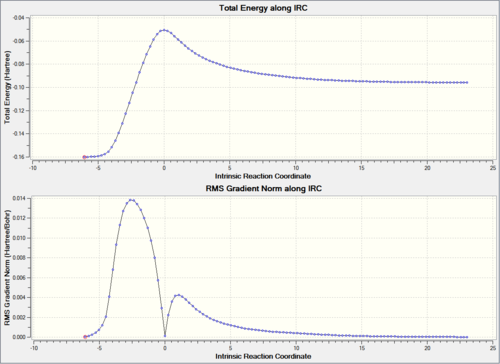
New C-C bond length (Å)	1.54	1.54

Table 18: A table to show the results from the IRC calculations of the two transition states

Table 18 shows that the output from the reaction showed the the exo and endo products for the corresponding transition states. The two products were drawn in Gaussian and the structures minimised using the AM1 semi-empirical molecular orbital method as above, to enable a comparison between these and the output from the IRC calculations. The products are shown in table 19.

The outputs from the IRC calculations showed the product had in fact been obtained as the energies for the final products were identical to the energies found in table 19. The bond lengths were also the same at 1.54 Å, this bond length compared very well to the literature value of 1.55 Å for sp³ bonded carbons.

It can also be seen that for the exo transition state the reaction path appears to have been calculated from product to reactants, instead of reactants to products as it has been for the endo calculation.

	Exo	Endo
Structure	DOI:10042/to-11365	DOI:10042/to-11366
Energy (kcal mol-1)	-100.34	-100.51
new C-C bond length (Å)	1.54	1.54

Table 19: A table to show the exo and endo products of the reaction between cyclohexadiene and maleic anhydride

A comparison of the total energies of the products showed that endo product was only 0.17 kcal mol^-1 more stable than the exo product. This exercise showed that instead of the exo being the thermodynamic product as expected with the Diels alder reaction, the endo conformer was both the thermodynamic and kinetic product due to sterics and secondary orbital effects.