Jump to content

Rep:Mod:NishMeisterG

From ChemWiki

Nisha Mistry

Module 1: Modelling Using Molecular Mechanics

Aims

Molecular models are used to visualise molecules in 3D which is an important tool in understanding their structure and reactivity. Molecular Mechanics (MM) is one approach for modelling molecules without the need for quantum mechanical methods. In this module is it used to predict the geometry and regioselectivity of different reactions by using the sum of the bond properties to express molecular properties. The implementation of the MM model used in this module is known as MM2.[1] Semi-empirical and DFT molecular orbital theory are used to investigate regioselectivity and neighbouring group participation.

Cyclopentadiene

The Dimerisation of Cyclopentadiene

Cyclopentadiene is of high importance due to its anion, C5H5-, being a very good metal ligand, particularly in sandwich compounds such as ferrocene.[2]The dimerisation of cyclopentadiene occurs through a Diels-Alder reaction, the result of this is that the product is formed in two different isomers, the endo and the exo forms. 1 below is the exo form and 2 is the endo form. Of these two products, one is more thermodynamically stable, i.e. has a lower energy than the other, and one is more kinetically stable, i.e. is formed faster than the other, because the transition state has a lower energy.

Figure 1: Reaction between two cyclopentadiene molecules
Energy (kcal/mol)
Cyclopentadiene Dimer Exo Dimer (1) Endo Dimer (2)
Stretch 1.2852 1.2508
Bend 20.5811 20.8477
Stretch-bend -0.8381 -0.8359
Torsion 7.6542 9.5114
Non-1,4 VDW -1.4171 -1.5441
1,4 VDW 4.2338 4.3201
Dipole/Dipole 0.3775 0.4477
Total Energy 31.8765 33.9975

Table 1: A table to show the relative energies of the cyclopentadiene dimers

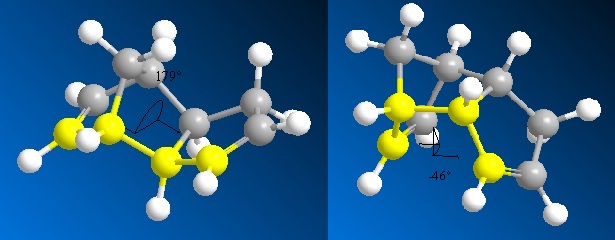
Table 1 below shows that the exo dimer is lower in energy by 2.121 kcal/mol, and therefore more thermodynamically stable. This is because of the torsional strain. Figure 2 shows the dihedral angles of the two dimers. From this it can be seen that the dihedral angle in the exo dimer is 179°, which makes the highlighted bonds almost anti periplanar to each other. This is the most favourable conformation. The dihedral angle for the endo dimer is 46°, which is not a favourable angle.

Figure 2: Torsional Strain on exo dimer (left) and endo dimer (right)

However it is known that the endo dimer is formed almost exclusively in the Diels Alder reaction.[3] This means the that product formed in the dimerisation of cyclopentadiene is the kinetic product. Since it is the kinetic product it has the lowest energy transition state. This is due to favourable orbital contributions, which are not taken into account by the MM2 method. The orbitals interactions are shown in figure 3 below.

Figure 3: Orbital interactions in the transition states on forming the exo (a) and endo (b) dimers

The Hydrogenation of the Cyclopentadiene Dimer

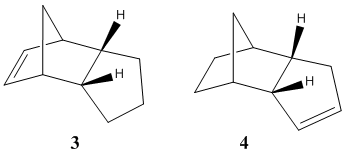
The hydrogenation of the cyclopentadiene dimer yields the two different dihydro products which shown below. The tetrahydro derivative is only formed after prolonged hydrogenation.

Figure 4: The two products from the hydrogenation of the cyclopentadiene dimer

The geometries of the two structures were minimised using the MM2 force field, the results of which are shown in the table below.

Energy (kcal/mol)
Dihydro Cyclopentadiene Dimer Dihydro Dimer (3) Dihydro Dimer (4)
Stretch 1.2774 1.0959
Bend 19.8622 14.5244
Stretch-bend -0.8347 -0.5489
Torsion 10.8091 12.4977
Non-1,4 VDW -1.2234 -1.0695
1,4 VDW 5.6324 4.5119
Dipole/Dipole 0.1621 0.1406
Total Energy 35.6850 31.1520

Table 2: A table to show the relative energies of the dihydro cyclopentadiene dimers

The results show that structure 4 is more stable than structure 3 by a total energy of 4.533 kcal/mol. This is result is mostly influences by the bending energy. For dimer 3, the bending energy was 19.8622 kcal/mol, this is significantly greater than the bending energy for dimer 4 which was only 14.5244 kcal/mol. This is reflected in the bond angles which are shown below in figure 5. The bond angle for dimer 3 was 108° and for dimer 4 was 112°. The ideal bond angle for a C=C-C bond is 120° and since the angle in dimer 3 is smaller this means that there is more bending strain and therefore it is higher in energy. The torsional strain is higher in energy for dimer 4 however bending strain is more dominant.

A study of frontier orbital theory is required to determine if the reaction is under kinetic or thermodynamic control.

Figure 5: Bond angles for dimer 3 (left) and dimer 4 (right)

Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

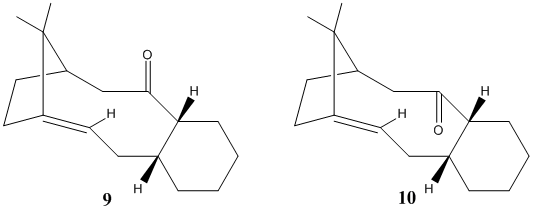
An intermediate in the synthesis of Taxol can be synthesised with the carbonyl group up or the carbonyl group down. The compound can isomerise to the other carbonyl isomer on standing. The two intermediates, 9 and 10, shown below in figure 6, are atropisomers. Atropisomers are conformers which arise from the restricted rotation around a single bond and can be isolated as different chemical species.[4] Using the MM2 force field, the energy of the two intermediates has been minimised.

Figure 6: A key intermediate in the synthesis of Taxol with the carbonyl group up (9) and down (10)

The intermediates can be both in the chair or twist boat conformation, however the twist boat is much higher in energy[5] and so is not included in this discussion. For Intermediate 9, using MM2 to minimise the energy, the energy of the twist boat was 53.01 kcal/mol.For Intermediate 10 the energy of the twist boat was 46.45 kcal/mol.

Energy (kcal/mol)
Intermediate 9 Intermediate 10
Stretch 2.7840 2.6019
Bend 16.5378 10.4163
Stretch-bend 0.4297 0.2905
Torsion 18.2498 19.3815
Non-1,4 VDW -1.5437 -2.2177
1,4 VDW 13.1067 12.9171
Dipole/Dipole -1.7247 -2.0088
Total Energy MM2 47.8396 41.3809
Total Energy MMFF94 70.5431 61.2094

Table 3: A table to show the relative energies of the two intermediates of Taxol

From the table above, it can be seen that intermediate 10 was the more stable isomer as the total energy was 6.46 kcal/mol lower in energy than intermediate 9. The largest contributing factor to the stability of intermediate 10 is the bending energy, which is 6.12 kcal/mol lower in energy for intermediate 10 than for intermediate 9. The unexpected stability of these intermediates is due to 'hyperstability', which is where the olefins contain less strain than the parent hydrocarbon.[6] These structures are unreactive because of the cage type structure of the olefin, providing extra stability to the isomer.

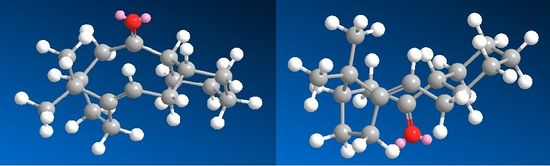
Figure 7: Left - Intermediate (9) - total energy = 47.8396 kcal/mol, Right - Intermediate (10) - total energy = 41.3809 kcal/mol

The alkene reacts very slowly because the alkane product is higher in energy, which makes the reaction of the alkene unfavourable. The minimised energy for the hydrogenation product of intermediate 10 was 48.69 kcal/mol, which was 7.31 kcal/mol higher in energy. Table 4 shows the energy breakdown for the saturated product.

Energy (kcal/mol)
Figure 8: Hydrogenation product of intermediate 10
Stretch 2.6743
Bend 12.1060
Stretch-bend 0.58.17
Torsion 22.8396
Non-1,4 VDW -2.6085
1,4 VDW 15.5192
Dipole/Dipole -1.7324
Total Energy MM2 49.3798
Total Energy MMFF94 69.5409

Table 4: A table to show the relative energies of the hydrogenation product of intermediate 10

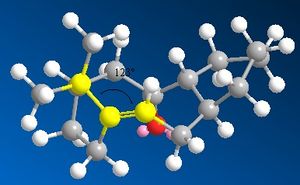
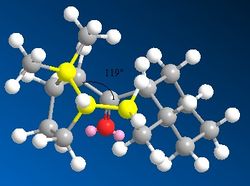
By comparing the date found in table 3 and table 4, it can be seen that the bending energy is one of the largest contributors to the raise in energy. From a study of the bond angles, it can be seen that the bond angle in intermediate 10 is 123° which is incredibly close to the ideal angle of 120° for an sp2 carbon. However, the saturated product has a bond angle across the bridge head of 119°, which is causing extra strain to the molecule considering that the ideal sp3 bond angle is 109.5°.

Intermediate 10 (olefinic) Intermediate 10 (saturated)
bond angle: 123°
bond angle: 119°
Figure 9: Bond angles for the olefin bridge head and saturated bridge head

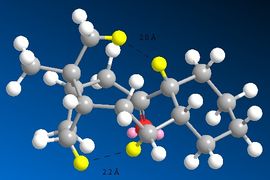
The other contributors to the raise in energy are 1,4 VDW interactions. On hydrogenation of the alkene, the H-H interaction become very replusive, as the lengths are 2.2 Å and 2.0 Å. compared to 2.2 Å and 2.1 Å in intermediate 10. Since this is an unfavourable interaction the energy is raised.

Intermediate 10 (olefinic) Intermediate 10 (saturated)
Repulsive Van der Waals interactions, 2.1 Å and 2.2 Å
bond angle: Repulsive Van der Waals interactions, 2.0 Å and 2.2 Å
Figure 10: Repulsive VDW forces for the olefin bridge head and saturated bridge head

Modelling Using Semi-empirical Molecular Orbital Theory

Regioselective Addition of Dichlorocarbene

Part 1

Orbital control of reactivity can be illustrated in the reaction of compound 12 with electrophilic reagents. The energy of the orbitals can be calculated and displayed graphically.

Figure 11: Compound 12

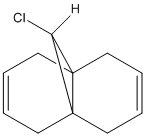
One such electrophilic reagent is chlorocarbene. The reaction of compound 12 with chlorocarbene can be rationalised using molecular orbitals and is shown to support the literature and experimental results. The literature states that the chlorocarbene reacts on the double bond endo to the chlorine and on the opposite face of the molecule to the chloropropyl ring.[7] The reactions mechanism for compound 12 and chlorocarbene is shown below.

Figure 12: The mechanism for the reaction between compound 12 and chlorocarbene

Firstly, using an MM2 force field, the energy of the compound was minimised. The results of this have been tabulated in table 5.

Energy (kcal/mol) Compound 12
Stretch 0.6185
Bend 4.7367
Stretch-bend 0.0398
Torsion 7.6577
Non-1,4 VDW -1.0654
1,4 VDW 5.7950
Dipole/Dipole 0.1123
Total Energy MM2 17.8945

Table 5: A table to show the minimised energies of compound 12

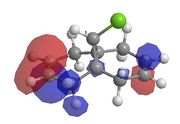
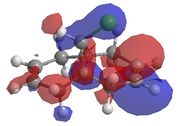
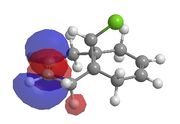
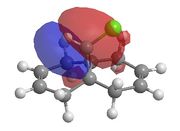
This method does not take into account the electrons in the bond and how this effects bonds, reactivity and spectroscopic properties. The MOPAC/PM6 MO method has been used to provide an approximate representation of the valence-electron molecular wavefunctions.[8]The energy obtained from the minimisation by MOPAC/PM6 was 19.740 kcal/mol. Representations of the HOMO-1, HOMO, LUMO, LUMO+1 and LUMO+2 are shown below.

HOMO-1 HOMO LUMO LUMO+1 LUMO+2
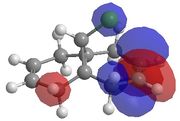Figure 13: Representations for some of the molecular orbitals of compound 12

From these results it is possible to determine the areas of high electron density. It can be seen from the HOMO that there is

Figure 14: MO diagram to show σ*-π interaction

higher electron density across the double bond which is endo to the chloropropyl ring. This makes the endo bond more nucleophilic than the exo bond and therefore making the endo C=C bond more reactive to attack by the electrophilic chlorocarbene.


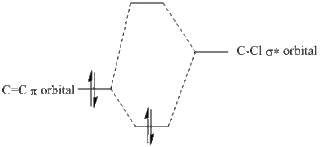
There is also a stabilising effect from the C-Cl σ* orbital to the exo C=C double bond. This C-Cl σ* orbital can clearly be seen in the representation of the LUMO+1 orbitals. The C-Cl σ* orbital interacts with the C=C π bonding orbital on the exo bond which can be seen in the representation of the HOMO-1 orbitals. This interaction can be displayed using a MO diagram, as shown in figure 13.

From looking at the orbitals above it is clear that no similar, favourable orbital interaction can be made with the C=C π bonding orbital on the endo bond. This explains the regioselectivity of this reaction.

Part 2

Compound 12 has been compared to its monohydrated version where the double bond exo (or anti) to the chlorine-carbon bond has been replaced with a carbon-carbon single bond. Using B3LYP/6-31G(d,p) Gaussian geometry optimization and frequency calculation, the vibrational frequencies of the two molecules were calculated. The IR spectra obtained from the calculations are shown below.

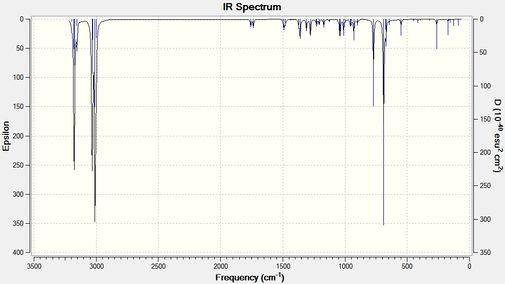
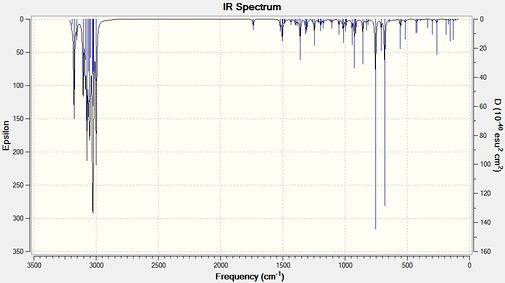
Figure 15: IR spectrum for Compound 12 Link to Dspace: http://hdl.handle.net/10042/to-10418
Figure 16: IR spectrum for the monohydrateed version of Compound 12 Link to Dspace: http://hdl.handle.net/10042/to-10419




















The table below shows the C-CL stretches and C=C stretches that have been found. The error in the predicted wavenumber is known to be approximately 8% so both the calculated values and corrected values have been tabulated.

Compound 12 Monohydrated Compound 12
C-Cl Stretch (cm-1) (corrected value) 770.91 (709.24) 756.12 (695.63)
C=C Stretch (endo)(cm-1) (corrected value) 1757.36 (1616.77) 1736.84 (1597.89)
C=C Stretch (exo)(cm-1) (corrected value) 1737.11 (1598.14) N/A

Table 6: A table to show the IR stretching frequencies of the C-Cl and C=C bonds

From the wavelengths above it can be seen that on removal of the exo C=C double bond, the C-Cl bond decreases indicating an increase in bond strength. This agrees with the analysis above since interactions between the C-Cl σ* orbital and the C=C π bonding orbital would weaken the C-Cl bond as the anti-bonding orbital gains (to a small extent) some electron density. The IRs show that the endo C=C double bond strength also increases on removal of the exo C=C double bond.

Monosaccharide Chemistry: Glycosidation

The glycosidation reaction is well known to produce the α-anomer (1,2-trans product) although the axial position in chair conformation is known to be higher in energy than the equatorial. This is due to the neighbouring group effect and stabilisation of the product due to electron donation into the Nu-C σ* orbital by the lone pairs on the oxygen in the ring. The figure below shows the mechanisms for the formations of the α-anomer and the β-anomer.

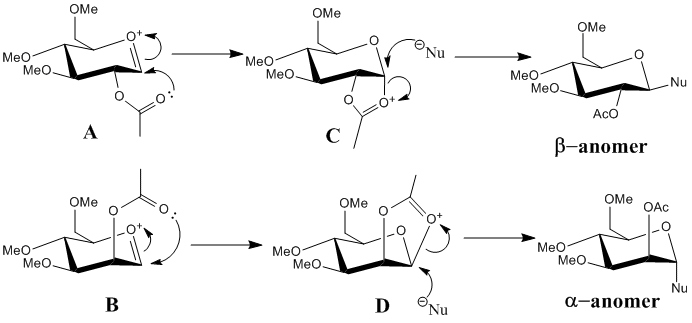
Figure 17: Mechanism for glycosidation to form the α- and β-anomers


Using MM2 and MOPAC/PM6 methods, the energies of structures A, B, C and D have been minimised. The energies and jmols for the structures are shown in the table below. A', B', C', and D', differ from the original molecules by whether the acyl group is above or below the plane of the oxonium ion.

Energy (kcal/mol)
Monosaccharide A Monosaccharide A' Monosaccharide B Monosaccharide B' Monosaccharide C Monosaccharide C' Monosaccharide D Monosaccharide D'
Stretch 2.8519 2.5493 2.8156 2.5768 2.0762 2.7115 1.8915 2.6179
Bend 11.5825 8.5970 10.7155 11.0959 14.1220 17.4764 20.7508 19.8546
Stretch-bend 1.0749 0.9210 0.9886 0.9405 0.7522 0.7956 0.7769 0.7770
Torsion 3.5117 3.5679 2.5349 1.3042 9.6737 8.1546 8.1065 6.6344
Non-1,4 VDW 1.5043 -2.5655 0.8526 -0.9340 -2.2883 -2.4147 -3.3239 -3.0817
1,4 VDW 18.86217 19.5152 18.9254 18.7639 17.8982 19.3921 17.0716 18.56.76
Charge/Dipole -23.0367 -1.4961 -21.4392 -12.3181 -9.5311 -0.3465 -4.9218 -0.7229
Dipole/Dipole 6.4541 3.1958 5.5009 4.7474 -2.0811 -1.7424 -1.7724 -1.2217
Total Energy MM2 22.8048 34.2847 20.8943 26.1766 30.6218 44.0265 38.5792 43.4252
Jmol MM2
Total Energy PM6 -91.66269 -77.39794 -88.72833 -77.50959 -91.66261 -66.85024 -88.72815 -67.00339
Jmol PM6
Acyl Above/ Below the plane of the oxonium ion Below Above Above Below Below Above Above Below

Table 6: A table to show the relative energies of the different monosaccharides

This table shows that the energy of A equals the energy of C and the energy of B equals the energy of D using the MOPAC/PM6 method. The MM2 method cannot account for the change in bonding, where-as the PM6 can since the acyl groups are in the correct orientation, and the method treats the neighbouring group effect as a non-classical carbocation, hence it gives the same energies. A non classical carbocation is one where the charge is not localised but distributed between the oxygen in the ring and the oxygen in the acyl group.[9]

The energies above clearly show that A, B, C and D are lower in energy than A', B', C' and D'. This explains the regioselectivity of the reactions shown in figure 17, since the conformations of A and B are lower in energy, and are more reactive than A' and B'. The charge/dipole interaction is the largest contributing factor to the differences in energy. These difference arise from the change in the position of the oxygens, which carry the most electron density, and the formal charges.

Mini Project using DFT-based Molecular Orbital Methods: Investigating the regioselectivity of the Baeyer-Villiger Reaction

The Baeyer-Villiger reaction oxidises ketones into esters by using as peracid.[10] The reaction scheme below shows the conversion of ketone 10 into esters 11 and 12 by m-chloroperbenzoic acid. The two products are known as β-lactams and are regioisomers. The calculations for this reaction were carried out using 3 different R groups, iso-propyl, tert-butyl, and phenyl. The results are shown below. The mechanism for this reaction is shown below in figure 18, where the red arrows form product 11, and the black form product 12.

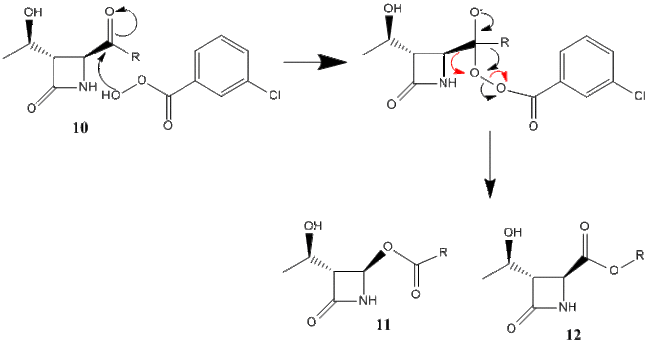
Figure 18: Mechanism for the conversion of ketone 10 into esters 11 and 12

Analysis of the NMR spectra below is the most effective method for discerning which product has been made in these reactions. The carbon and nitrogen NMR for each product are shown below.

Experimentally, when R=iPr, this reaction yields an equimolar mixture of both products.[11]

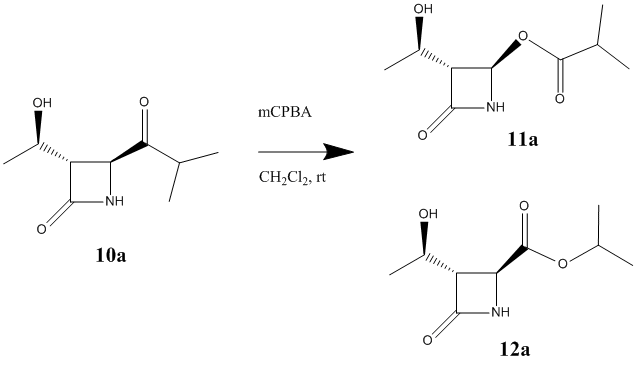
Figure 19: Reaction scheme for the conversion of ketone 10a into esters 11a and 12a

Using the MM2 force field and MOPAC/PM6 method the energy of the two products have been minimised. The results have been shown in the table below.

Energy (kcal/mol)
Isomer 11a Isomer 12a
Stretch 2.6139 2.1314
Bend 35.9920 36.8840
Stretch-bend -0.5435 -0.4504
Torsion 6.5900 8.4297
Non-1,4 VDW -2.7991 -6.8900
1,4 VDW 4.6560 6.9100
Dipole/Dipole -2.1392 -3.1995
Total Energy MM2 44.3702 44.8153
Jmol MM2
Total Energy PM6 -170.3962 -178.5153
Jmol PM6

Table 7: A table to show the relative energies of the two products

From the table above it can be seen that the energies for the two products are very similar and when minimised with MM2 are almost exactly the same with on a 0.44451 kcal/mol difference between them. However the MM2 method is not as accurate as the MOPAC/PM6 method, which in this case shows that there is a more significant energy difference between the two isomers. However the energies are still very similar indicating that the reaction would yield both products. The minimised energies for 11a and 12a, using Gaussian were -443147 kcal/mol and -443903 kcal/mol respectively. Links to Dspace: Product 11a:http://hdl.handle.net/10042/to-10420, product 12a:http://hdl.handle.net/10042/to-10421. This shows that using the most accurate method for optimisation the energies were in fact very similar, explaining why regioselectivity in this reaction is so poor. Shown below are the carbon and nitrogen NMRs for products 11a and 12a.

Figure 20: Carbon NMR of product 11a Link to Dspace for both C and N NMRs: http://hdl.handle.net/10042/to-10422
Figure 21: Carbon NMR of product 12a Link to Dspace for both C and N NMRs: http://hdl.handle.net/10042/to-10424
Figure 22: Nitrogen NMR of product 11a
Figure 23: Nitrogen NMR of product 12a



































From the carbon NMR, it is clear that in product 11a the 2 -C(CH3)2 iso-propyl carbons are degenerate where as in compound 12a they are not. This observation alone would be enough to know if only one of the products had formed. However this is not the only significant difference in the two spectra. C4 as on the spectra is the carbon atom in the 4-membered ring which is bonded to the ester group. When it is bonded directly to the carbonyl carbon as in product 12a, it is more deshielding therefore appears at a higher chemical shift (139.46 ppm) than when bound directly to the oxygen atom as in product 11a (112.97 ppm). The peaks obtained in these spectra have not compared well to the peaks obtained in the literature.[12] The nitrogen NMR shows the same trend in that when the carbonyl carbon is bound to the ring (product 12a) then the nitrogen is more deshielded and has a higher chemical shift of 132.95 ppm, compared to the chemical shift of 120.31 ppm for product 11a. This would be a good characteristic to use to identify the two different products.


As a second R group tert-butyl was used. Experimentally, it was found that 12b was the only product.[13] The reaction scheme for this reaction is shown in figure 24.

Figure 24: Reaction scheme for the conversion of ketone 10b into esters 11b and 12b

Using the MM2 force field and MOPAC/PM6 method the energy of the two products have been minimised. The results have been shown in the table below. The products were also minimised using Gaussian. The energies for products 11b and 12b were found to be -467821 kcal/mol and -468564 kcal/mol respectively. Link to Dspace for product 11b:http://hdl.handle.net/10042/to-10462 and product 12b: http://hdl.handle.net/10042/to-10465. These energy differences are more significant that for when R=iPr, and product 12b is much lower in energy. Both the MM2 and PM6 method of minimising the energies also agree with this data. This would explain why, experimentally, only product 12b is formed, since it is lower and energy and therefore easier to form.

Energy (kcal/mol)
Isomer 11b Isomer 12b
Stretch 2.8672 2.4519
Bend 36.1756 38.2602
Stretch-bend -0.4675 -0.4229
Torsion 7.3821 9.4489
Non-1,4 VDW -4.8054 -4.7894
1,4 VDW 5.8731 6.4023
Dipole/Dipole -1.94455 -3.1901
Total Energy MM2 45.0807 48.1610
Jmol MM2
Total Energy PM6 -175.0439 -190.4773
Jmol PM6

Table 8: A table to show the relative energies of the two products

Below are the carbon and nitrogen NMR spectra. A study of the resonances would give a good indication as to the structure of the product.

Figure 25: Carbon NMR of product 11b Link to Dspace for both C and N NMRs: http://hdl.handle.net/10042/to-10425
Figure 26: Carbon NMR of product 12b Link to Dspace for both C and N NMRs:http://hdl.handle.net/10042/to-10426
Figure 27: Nitrogen NMR of product 11b
Figure 28: Nitrogen NMR of product 12b


































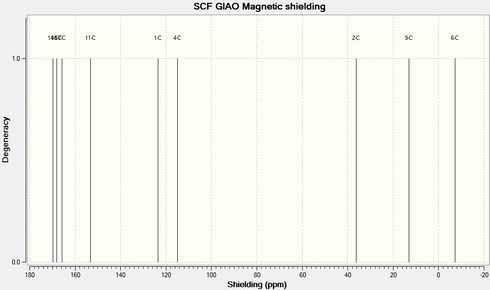
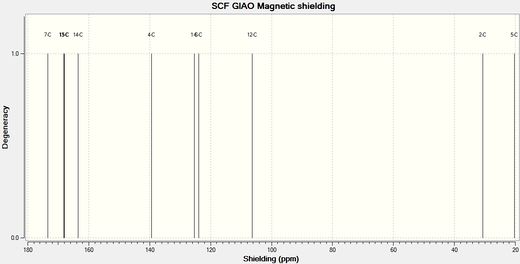
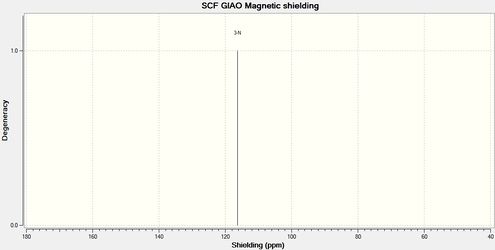
Looking at the carbon NMR spectrum it can be seen that C4, as described above as the carbon in the 4 membered ring, directly attached to either the carbonyl or the oxygen, has a different shift depending on if it bonded to another carbon or the oxygen. In product 12b, when it is bonded to the carbonyl carbon, C4 is more deshielded as so has a higher chemical shift than in product 11b. The nitrogen NMR shows a similar trend. In the spectrum for product 11b the nitrogen peak has a chemical shift of 116.33 ppm and in the spectrum for product 12b the peak has a chemical shift of 124.84 ppm, showing that in 12b the nitrogen is more deshielded. These two spectrum would clearly show that only product 12b had formed in this reaction.


As the third and final R group for this investigation, phenyl was used. Experimentally, it was found that 11c was the only product.[14] The reaction scheme for the formation of products 11c and 12c are shown below in figure 29.

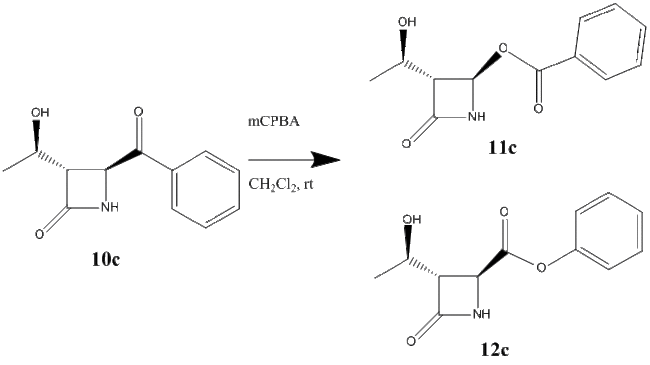
Figure 29: Reaction scheme for the conversion of ketone 10c into esters 11c and 12c

Using the MM2 force field and MOPAC/PM6 method the energy of the two products have been minimised. The results have been shown in the table below. The products were also minimised using Gaussian. The energies for products 11c and 12c were found to be -514119 kcal/mol and -514859 kcal/mol respectively. Link to Dspace for product 11b: http://hdl.handle.net/10042/to-10478 and product 12b: http://hdl.handle.net/10042/to-10479. All 3 minimisation methods show that product 12c is in fact the product which is lower in energy, however the Gaussian method (the most accurate) shows that the difference is comparatively very small. Sterics would be the decided factor as to which product is formed. The azetidinyl ring is a better migrating group that the phenyl ring, and looking back the mechanism in figure 18, the migration of this ring would yield product 11c.

Energy (kcal/mol)
Isomer 11c Isomer 12c
Stretch 3.1078 2.4990
Bend 39.2757 36.1799
Stretch-bend -0.5468 -0.5617
Torsion 1.5206 8.7154
Non-1,4 VDW -0.0231 -12.4082
1,4 VDW 9.4419 9.5300
Dipole/Dipole -0.9026 2.4768
Total Energy MM2 51.8734 46.4312
Jmol MM2
Total Energy PM6 -123.9512 -125.3455
Jmol PM6

Table 9: A table to show the relative energies of the two products

Below are the carbon and nitrogen NMR spectra for products 11c and 12c.

Figure 30: Carbon NMR of product 11c Link to Dspace for both C and N NMRs: http://hdl.handle.net/10042/to-10427
Figure 31: Carbon NMR of product 12cLink to Dspace for both C and N NMRs: http://hdl.handle.net/10042/to-10428
Figure 32: Nitrogen NMR of product 11c
Figure 33: Nitrogen NMR of product 12c




































These NMR would clearly show which of the two product is formed. In the carbon spectrum for products 11c and 12c C4 again shows a characteristic shift in chemical shift depending on whether the carbon atom is bound to another carbon atom or to an oxygen. In the spectrum for 12c where it would be joined to another carbon atom, it has a higher chemical shift of 140.07 ppm compared to 113.09 ppm in the spectrum of 11c, showing that it is more deshielded. The spectrum for product 11c also shows degeneracy for two of the phenyl carbons (14 and 16 at 69.73 ppm) whereas none of the phenyl carbons are degenerate in the spectrum for product 12c. In the nitrogen NMR, a similar trend is seen with a peak at 112.03 ppm for the nitrogen in 11c but a peak at 129.92 ppm for the nitrogen in product 12c, showing that, again, this nitrogen is more deshielded. These factors would make it clear as to which product had been formed in the reaction as shown in figure 29.


In summary, the energies are not a good indication as to which product would be formed as it does not take into account factors such as sterics or the degree to which the R groups are good migrating groups. NMR is clearly a good way of identifying which products have been obtained in the reactions as there are characteristic shifts for C4 and the nitrogen in the 4-membered ring depending on which ester has been formed.

References

  1. ↑ http://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:molecular_mechanics
  2. ↑ Wilkinson, G., Rosenblum, M., Whiting, M. C., Woodward, R. B., "The Structure of Iron Bis-Cyclopentadienyl", J. Am. Chem. Soc., 1952, 74(8), pp. 2125-26,DOI:10.1021/ja01128a527
  3. ↑ J. E. Baldwin, J. Org. Chem., 1966, 31, 2441-2444 DOI:10.1021/jo01346a003
  4. ↑ http://goldbook.iupac.org/A00511.html IUPAC Gold Book, accessed 21/11/11
  5. ↑ S. W. Elmore and L. Paquette, Tetrahedron Letters, 1991, 319 DOI:S0040403900926170
  6. ↑ W. F. Maier, P. V. R. Schley J. Am. Chem. Soc., 1981, 103 (8), pp 1891–1900DOI:10.1021/ja00398a003
  7. ↑ B. Halton, R. Boese and H. S. Rzepa, J. Chem. Soc., Perkin Trans. 2, 1992, 447-448 DOI:10.1039/p29920000447
  8. ↑ https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:organic
  9. ↑ J. D. Roberts, R. H. Mazur J. Am. Chem. Soc., 1951, 73 (7), pp 3542-3543 DOI:10.1021/ja01151a550
  10. ↑ Renz, M. and Meunier, B. (1999), 100 Years of Baeyer–Villiger Oxidations. European Journal of Organic Chemistry, 1999: 737–750. DOI:10.1002/%28SICI%291099-0690%28199904%291999:4%3C737::AID-EJOC737%3E3.0.CO;2-B
  11. ↑ M. Laurent, M. Cérésiat, and J. Marchand-Brynaert, J. Org. Chem., 2004, 69 (9), pp 3194–3197 DOI:10.1021/jo030377y
  12. ↑ M. Laurent, M. Cérésiat, and J. Marchand-Brynaert, J. Org. Chem., 2004, 69 (9), pp 3194–3197 DOI:10.1021/jo030377y
  13. ↑ M. Laurent, M. Cérésiat, and J. Marchand-Brynaert, J. Org. Chem., 2004, 69 (9), pp 3194–3197 DOI:10.1021/jo030377y
  14. ↑ M. Laurent, M. Cérésiat, and J. Marchand-Brynaert, J. Org. Chem., 2004, 69 (9), pp 3194–3197 DOI:10.1021/jo030377y
Retrieved from "https://chemwiki.ch.ic.ac.uk/index.php?title=Rep:Mod:NishMeisterG&oldid=817612"