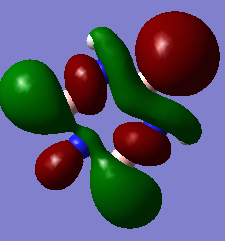
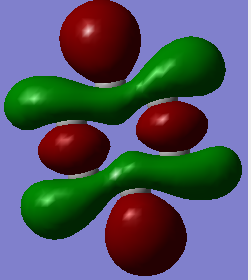
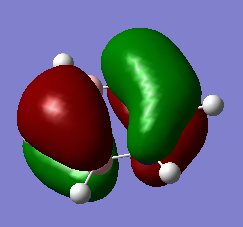
Rep:Mod:NKXYZ123
BH3
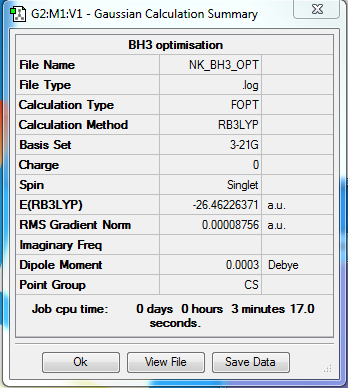
B3LYP/3-21G level
Optimisation Summary
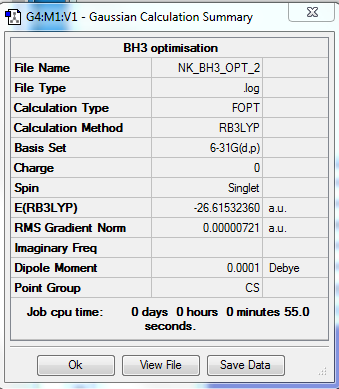
B3LYP/6-31G level
Optimisation Summary
Summary Table
Item Value Threshold Converged? Maximum Force 0.000217 0.000450 YES RMS Force 0.000105 0.000300 YES Maximum Displacement 0.000919 0.001800 YES RMS Displacement 0.000441 0.001200 YES
Frequency analysis log file narayankuleindiren_bh3_freq.log
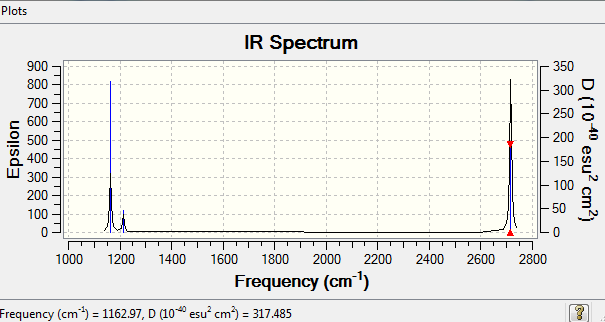
Low frequencies --- -7.9073 -1.6385 -0.0053 0.6256 6.5697 6.7709 Low frequencies --- 1162.9662 1213.1623 1213.1650
BH3 |
Vibrational spectrum for BH3
| wavenumber (cm-1 | Intensity (arbitrary units) | symmetry | IR active? | type |
| 1163 | 93 | A2” | yes | out-of-plane bend |
| 1213 | 14 | E | very slight | bend |
| 1213 | 14 | E | very slight | bend |
| 2582 | 0 | A1‘ | no | symmetric stretch |
| 2716 | 126 | E’ | yes | asymmetric stretch |
| 2716 | 126 | E’ | yes | asymmetric stretch |
IR Of BH3
|
There are fewer peaks than vibrational modes as some of the vibrational modes show no change in dipole moment.
MO for BH3:
|
The 3D models mirror the drawn MOs, hence showing the accuracy of the model
Smf115 (talk) 00:06, 17 May 2018 (BST)Correct assignments and the accuracy is noticed, hwoever, the comment is a little brief and consider the subtle differences between the MOs and the LCAOs.
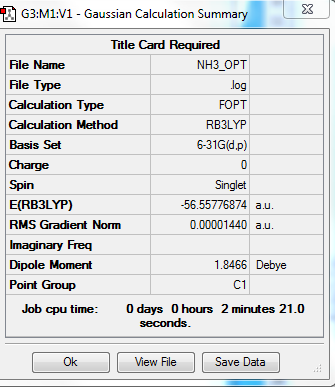
NH3
B3LYP/6-31G level
Optimisation Summary
Summary Table
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
Frequency analysis log file NK_nh3_freq.log
Low frequencies --- -0.0013 -0.0012 0.0015 12.1922 16.3313 18.2402 Low frequencies --- 1089.5725 1693.9569 1694.0197
NH3 |
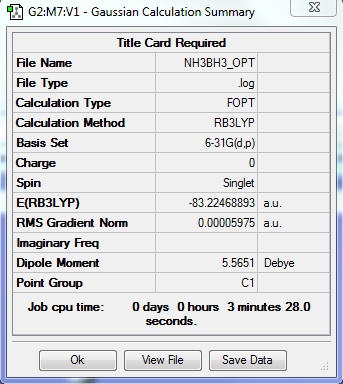
NH3BH3
B3LYP/6-31G level
Optimisation Summary
Summary Table
Item Value Threshold Converged? Maximum Force 0.000115 0.000450 YES RMS Force 0.000060 0.000300 YES Maximum Displacement 0.000581 0.001800 YES RMS Displacement 0.000345 0.001200 YES
Frequency analysis log file nk_nh3bh3_freq.log
Low frequencies --- -0.0007 0.0004 0.0009 16.1826 17.3444 37.1736 Low frequencies --- 265.8334 632.2043 639.2681
NH3BH3 |
E(NH3)= -56.55776874
E(BH3)= -26.6153236
E(NH3BH3)= -83.22468893
ΔE=[E(NH3)+E(BH3)] - E(NH3BH3)
Dissociation energy = 0.05159659 au
Dissociation energy = 136 kJ / mol
It is a relatively weak bond with a lower dissociation energy than O-O (142kJ/mol) another relatively weak bond.[1]
Smf115 (talk) 22:37, 15 May 2018 (BST)Great calculation with the correct accuracy for the energy values given and a well referenced comparison given.
BBr3
B3LYP/6-31G level
Optimisation Summary
Summary Table
Item Value Threshold Converged? Maximum Force 0.000008 0.000450 YES RMS Force 0.000005 0.000300 YES Maximum Displacement 0.000035 0.001800 YES RMS Displacement 0.000023 0.001200 YES
Frequency analysis log file NK_F_BBR3.log
Low frequencies --- -2.2522 -0.0002 -0.0001 0.0001 0.2464 0.9431 Low frequencies --- 155.9350 155.9462 267.6888
BBr3 |
My link: http://hdl.handle.net/10042/202340
Benzene
B3LYP/6-31G level
Optimisation Summary
Summary Table
Item Value Threshold Converged? Maximum Force 0.000198 0.000450 YES RMS Force 0.000082 0.000300 YES Maximum Displacement 0.000849 0.001800 YES RMS Displacement 0.000305 0.001200 YES
Frequency analysis log file nk_benzene_freq.log
Low frequencies --- -13.7810 -12.9763 -11.9029 -0.0008 -0.0001 0.0004 Low frequencies --- 414.0699 414.1914 620.9703
Benzene |
Borazine
B3LYP/6-31G level
Optimisation Summary
Summary Table
Item Value Threshold Converged? Maximum Force 0.000085 0.000450 YES RMS Force 0.000033 0.000300 YES Maximum Displacement 0.000249 0.001800 YES RMS Displacement 0.000077 0.001200 YES
Frequency analysis log file nk_benzene_freq_1.log
Low frequencies --- -5.4002 -0.0012 -0.0010 -0.0009 6.1075 8.7467 Low frequencies --- 289.5706 289.6717 404.3335
Borazine |
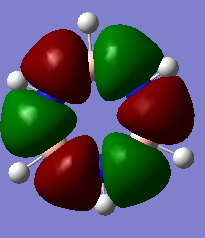
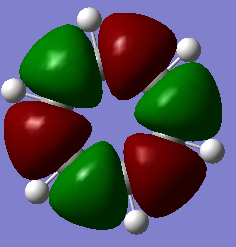
Borazine Vs. Benzene
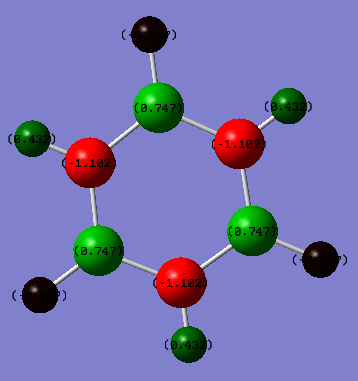
Charge Distribution
| Borazine | Benzene |
|---|---|
|
|
The formal charges are printed in the tables below
| Benzene | Charge (NBO) |
|---|---|
| Carbon | −0.239 |
| Hydrogen | 0.239 |
| Borazine | Charge (NBO) |
|---|---|
| Boron | 0.747 |
| Nitrogen | −1.102 |
| Hydrogen (B-H) | −0.077 |
| Hydrogen (N-H) | 0.432 |
It can be seen that different charges occur on the borazine ring compared with the benzene ring. On the benzene ring all of the six carbons are equivalent and hence the electronegativities of each atom on the ring is equal. All of the hydrogens in the ring are also in equivalent environments as they are all equivalent and attached to an equivalent carbons. This can be seen in the D6h symmetry. The carbon atoms are more electronegative than the hydrogen (2.55 (C) and 2.20 (H))[2] therefore the electrons are more attracted to the carbon atom. This explains the negative charge on the carbon and the more positive charge on the hydrogen atoms. Hence the charge distribution on each individual carbon and each individual hydrogen is equally distributed around the ring.
However nitrogen has a larger electronegativity than boron (3.04 (N) and 2.04 (B))[2] this means that the electrons are more attracted to each nitrogen atom and the charges are distributed unevenly between the nitrogen and the boron. The nitrogen therefore attracts the electrons more strongly giving it a more negative charge than boron. Borazine also differs from benzene as the charge on the hydrogen is dependent upon which atom it is connected to, either boron or nitrogen. Again the relative charge distributions can be explained by the relative electronegativities (2.20 (H))[2], as hydrogen is less electronegative than nitrogen the hydrogen atoms connected to the nitrogens have a more positive charge distribution. As hydrogen is more electronegative than boron the hydrogen atoms connected to the boron atoms have a negative electron distribution.
Smf115 (talk) 00:05, 17 May 2018 (BST)Excellent analysis of the charges and the colour range of the charge distribution across the molecules is correct.
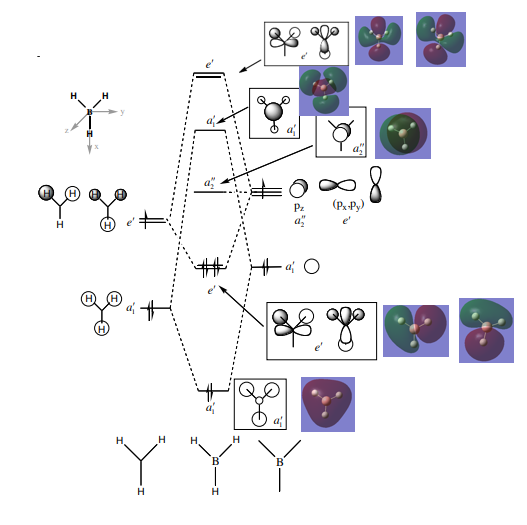
MO Comparisons
| Borazine | Benzene | Comparison |
|---|---|---|
 MO15
|
 MO14
|
These two MOs are very similar but do have a very subtle difference. They both correspond to higher energy sigma bonding MOs, the benzene MO is completely symmetric as each carbon is equivalent and contributes equally. However for the borazine the orbitals will slightly differ due to the differing contributions from the boron and the nitrogen. |
 MO19
|
 MO19
|
In these two MOs the differences between the MOs can be seen more clearly. They are both sigma anti-bonding orbitals. In the benzene due to the equivalence of the carbons the MO is symmetric. However in borazine, as boron is higher in energy than nitrogen it contributes more to the orbital than nitrogen and hence the MO is distorted towards the boron atom. |
 MO21
|
 MO21
|
These are both pi bonding MOs. Again the benzene MO is symmetric but the shape of the borazine MO is distorted due to the differing energies of the boron and the nitrogen atom. |
Smf115 (talk) 00:04, 17 May 2018 (BST)Good MO comparison with use of correct terminology. To improve, when mentioning symmetry a more thorough description, such as point group or symmetry element, could be given.
Aromaticity
Aromaticity is used to describe a cyclic, planar molecule with a ring of resonance bonds that exhibits more stability than other geometric or connective arrangements with the same set of atoms. Hückel's rule is used to predict if a planar ring molecule will have aromatic properties. According to the rule the criteria for a simple aromatic system are as follows:
1. The molecule must have 4n + 2 electrons in a conjugated system of p orbitals
2. The molecule must be planar
3. The molecule must be cyclic
4. The molecule must have a continuous ring of p atomic orbitals
The traditionally held view is that aromaticity arises from the overlap of pz orbitals in a plane creating a π system in which electrons are delocalised, and this the cause of the extra stability. This concept of overlapping pz orbitals works well for simple molecules such as benzene, however the model breaks down when considering more complex model. Both pyrene and coronene are aromatic and break the 4n + 2 rule [3]. Aromatic systems do not need to be planar either a well observed example is oath- and para- cyclophanes [4] There are also other non traditional examples such as metallobenzenes and spherical systems such as fullerenes. For approximately the past half-century it has been suggested that the traditional view that the aromatic stability is simply and only due to π-electron delocalisation is being challenged. It has been suggested that the σ-electrons may also be of importance, a lively debate topic in recent years. [5] MO theory is useful for explaining and visualising aromaticity as on of the main concepts shows how lone pairs of electrons are not contained in localized bonds such as in the valence bond theory but instead electrons can exist in molecular orbitals that are spread over the entire molecule. This explains a lot of the main aromatic properties such as common bond lengths
Smf115 (talk) 00:02, 17 May 2018 (BST)A well referenced and thorough discussion of aromaticity.
Smf115 (talk) 00:07, 17 May 2018 (BST)Overall a good wiki report with a strong project section.
References
- ↑ http://www.wiredchemist.com/chemistry/data/bond_energies_lengths.html
- ↑ 2.0 2.1 2.2 https://sciencenotes.org/list-of-electronegativity-values-of-the-elements/
- ↑ Roberts, John D.; Streitwieser, Andrew, Jr.; Regan, Clare M. (1952). "Small-Ring Compounds. X. Molecular Orbital Calculations of Properties of Some Small-Ring Hydrocarbons and Free Radicals". J. Am. Chem. Soc. 74 (18): 4579–82. doi:10.1021/ja01138a038.
- ↑ ]a)L.W.Jenneskens,J.C.Klammer,H.J.R.deBoer,W.H.deWolf, F.Bickelhoupt,C.H.Stam,Angew.Chem.1984,96,236;Angew. Chem. Int. Ed. Engl. 1984, 23, 238; b) F. Bickelhoupt, Pure Appl. Chem. 1990, 62, 373; c) F. Dijsktra, J. H. van Lenthe, Int. J. Quant. Chem. 1999, 74, 213; d) B. Ma, H. M. Sulzbach, R. B. Remington, H. F. Schaefer III J. Am. Chem. Soc. 1995, 117, 8392.
- ↑ Palusiak, M. and Krygowski, T. (2007), Application of AIM Parameters at Ring Critical Points for Estimation of π‐Electron Delocalization in Six‐Membered Aromatic and Quasi‐Aromatic Rings. Chemistry – A European Journal, 13: 7996-8006. doi:10.1002/chem.200700250