To view the molecules mentioned in this Wiki dynamically, please click here.

Module 3: Transition Structures

The computational study of transition structures is useful both as a method of studying a reaction and as a predictive tool for determining the likely structure of the products or the reactants. It can be used to assess the energy barrier a reaction faces and give an understanding of the mechanism through an assessment of the associated molecular orbitals. It is a powerful tool in the chemical toolbox, both for investigating the reactions we don't understand and for clarifying the reactions we do.

This Wiki will discuss the exercises and calculations set out in the Transition Sates script.

The Cope Rearrangement Tutorial

Optimizing the Reactants and Products

Throughout this section, reference is made to the conformations of 1,5-hexadiene, the structures of which may be found here.

a)

A structure of 1,5-hexadiene with an "anti" linkage was created from the cyclohexane fragment and optimised to a minimum at the HF/3-21G level of theory. It turned out to be the anti1 conformation, with energy -231.69260235 hartrees and point group C2

b)

A structure of 1,5-hexadiene with an "gauche" linkage was created from the cyclohexane fragment and optimised to a minimum at the HF/3-21G level of theory. It turned out to be the gauche6 conformation, with energy -231.68916020 hartrees and point group C1

As expected, the conformation generated for b) was of higher energy than that generated for a) due to the steric clashes a gauche linkage requires.

c)

anti2 looks as though it might be the lowest energy conformer, as it seems to have the fewest steric interactions. It was created from the cyclohexane fragment and optimised to a minimum at the HF/3-21G level of theory. It has energy -231.69253523 hartrees and point group C_i.

gauche3 was created from the cyclohexane fragment and optimised to a minimum at the HF/3-21G level of theory. It has energy -231.69266122 hartrees and point group C1.

The π* orbitals in anti1, anti2 and gauche3 all conjugate with σ* orbitals on the corresponding 3 or 4 atom. This creates a shortening and a strengthening on the C₂-C₃ and C₄-C₅ bonds. In anti1 and anti2, this conjugation is with C-C antibonds; in gauche3, it is with C-H antibonds. gauche3 is therefore less destabilised by this interaction.

anti1

anti2

gauche3

Nf710 (talk) 12:41, 25 April 2016 (BST) Good understanding, you could have better shown this with jmols of the orbitals

d)

The structures created in a) were anti1 and gauche6.

e)

anti2 was created in c). The energy is in good agreement with that provided.

f)

anti2 was optimised to a further minimum at the B3LYP/6-31G* level. It was returned with energy -234.61171062 hartrees and point group C_i. The geometry barely changed.

Nf710 (talk) 12:47, 25 April 2016 (BST) Nice use of jmol, but you should have looked at bond angles

g)

A frequency calculation was run on anti2 at the B3LYP/6-31G* level. There were no imaginary frequencies in the resulting Vibrations output.

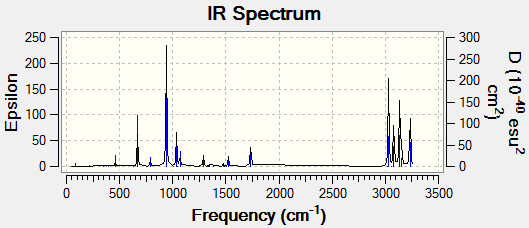
Sum of electronic and zero-point Energies / hartrees	Sum of electronic and thermal Energies / hartrees	Sum of electronic and thermal Enthalpies / hartrees	Sum of electronic and thermal free Energies /hartrees
-234.469219	-234.461869	-234.460925	-234.500809

Optimizing the "Chair" and "Boat" Transition Structures

a)

A first guess at the 1,5-cyclohexadiene chair transition structure was constructed out of two (CH₂-CH-CH₂) units, which in turn were created from the propane fragment.

b)

The 1,5-hexadiene chair was optimised to a transition state using the Berny method at the HF/3-21G level. At the same time, a frequency calculation was run on it. There was one imaginary frequency at -187.91 cm^-1, in line with expectation. Imaginary frequencies are the compuational manifestation of the restoring force of the quantum harmonic oscilator, acting against bond formation. If there were a bond there, it would resonate at the same magnitude of frequency. As there is no bond, we can only imagine - and calculate - what it would be like if there were one.

Nf710 (talk) 12:53, 25 April 2016 (BST) This is quite a strange way to explain it. its just the second derivative of the PES for that degree of freedom obviosuly you mean -817cm-1

c)

An optimisation of the 1,5-hexadiene chair was set up using frozen coordinates. The atoms that would be forming bonds were frozen and the rest of the molecule was optimised to a transition state using the Berny method at the HF/3-21G level.

d)

An optimisation of the 1,5-hexadiene chair was set up using unfrozen coordinates. The atoms that would be forming bonds were set to derivative and the molecule was optimised to a transition state using the Berny method at the HF/3-21G level.

	b) Standard Optimisation	c,d) Frozen Optimisation
C₁-C₆ new bond length / Å	2.02049	2.02069
C₃-C₄ new bond length / Å	2.02036	2.02059

The geometries of the two structures are very similar. The standard optimisation produced slightly shorter bond lengths, but the two methods give very similar results.

e)

1,5-hexadiene boat was optimised to a transition state using the QST2 method at the HF/3-21G level. It produced a viable transition structure with an imaginary frequency of -839.62 cm^-1

f)

Predictions of which conformers lead from which transition state

Chair TS	Boat TS
gauche2	gauche1
gauche5	gauche3
anti1	gauche 4
	gauche6
	anti2
	anti3
	anti4

An IRC optimisation was performed on the chair transition structure. It was chosen that the optimisation should proceed only in the forwards direction (as it would be symmetrical), that the force constant should be calculated at every step and that there should be 60 steps. When the calculation ran out of steps, it was observed that the structure looked similar to gauche2. Therefore, a normal optimisation to minimum at the HF/3-21G level was run, giving gauche2. After the IRC, the energy was -231.69157889 hartrees and the point group was C1. After the second optimisation, the energy was -231.69166702 and the point group was C2.

Nf710 (talk) 12:58, 25 April 2016 (BST) Correct conformer detrmined

g)

Both chair and boat structures were optimised to a transition state using the Berny method at the B3LYP/6-31G* level.

anti2

chair form

boat form

Click here for a dynamic
version of these molecules

Energy / hartrees

-234.61171062

-234.54309263

-234.55698303

Energy / kcal mol^-1

-32.32

-31.64

Imaginary IR frequency / cm^-1

-806.45

-812.20

Nf710 (talk) 13:05, 25 April 2016 (BST) The IR streches you give here are not the same as the ones in the appendix you have provided?

Nf710 (talk) 13:02, 25 April 2016 (BST) Those streches are not correct, you also ahvent worked out the activation energy or compared it to experiment. You have done some very nice formatting with Jmol, but you havent really shown that much of an understanding of the computational methods etc.

The Diels-Alder Cycloaddition

The reaction of butadiene and ethylene

Cis-butadiene and ethylene were created from the n-butane and ethane pre-loaded fragments respectively and were optimised to a minimum at the semi-empirical AM1 level. Their addition transition state was created from the bicyclo[2.2.2]octane pre-loaded fragment with an inter-fragment distance was set to 2.2 Å and (after a few attempts without the opt=NoEigen keyword) was optimised to a transition state using the Berny method at the semi-empirical AM1 level. There was a single imaginary vibrational frequency at -955.99 cm^-1, indicating that this was a transition state.

The two new bonds are being formed synchronously. The four carbon atoms are extending directly towards each other at the same time. In contrast, the lowest real (positive) frequency is given by a transverse vibration: the two fragments rotate with respect to each other, in turn drawing each pair of carbon atoms closer together and temporarily increasing the bond order of each bond. This is asynchronous bond formation.

The HOMO-LUMO pairs in butadiene and ethylene must be of the right symmetry in order to be able to react. As can be seen from their calculated molecular orbitals (below), they are indeed. Not only are they of just the right symmetries, but they align in space well and have good orbital overlap. The two orbitals forming the transition state HOMO are antisymmetric relative to the plane of symmetry of the transition state, making the HOMO antisymmetric, and those forming the LUMO are symmetric, which makes the LUMO symmetric. The reaction is favoured by there being multiple MOs interacting. For this reason, Diels-Alder is a fairly facile reaction, and it can be favoured further, as will be seen below.

The partly formed bonds are calculated to be 2.12 Å long. To put this in context, the appropriately named A Bondi puts the mean van der Waals radius of carbon at 1.70 Å.^[1] Experimental data shows C-C bond lengths in cyclohexene to be around 1.5 Å, with the C3-C4 bond (i.e. the one that is being formed here) measured at 1.515 ± 0.020 Å.^[2] The two atoms are much closer to the 1.5 Å of a bond than to the 3.4 Å separation they would have with no bonding interaction. This suggests the two molecules are well on their way to becoming one at the transition state.

Ciang and Bauer give the cyclohexene C₁=C₂ bond length as 1.335 ± 0.003 Å. This happenes to be closer to the calculated lengths of the other bonds in the molecule than the value for single bonded C-C. Not only that, but the three bonds that were double bonds in the separate molecules remain the shortest in the transition structure. This suggests that the molecule is, in fact, not as far along the reaction coordinate as it seemed and the π bonds retain a lot of their character (although some π density is moving away from the old bonds and into the new ones).

(Nice intro. Refreshing to see some humour. Perhaps some general theory to serve as an introduction is needed? Tam10 (talk) 11:24, 14 April 2016 (BST))

Ethylene HOMO: symmetric (s) relative to TS plane of symmetry			Cyclohexene TS LUMO: symmetric (s) relative to TS plane of symmetry
Butadiene LUMO: symmetric (s) relative to TS plane of symmetry
Ethylene LUMO: antisymmetric (a) relative to TS plane of symmetry			Cyclohexene TS HOMO: antisymmetric (a) relative to TS plane of symmetry
Butadiene HOMO: antisymmetric (a) relative to TS plane of symmetry

The reaction of cyclohexa-1,3-diene and maleic anhydride

The transition structures were created by adding to and modifying the atoms in the Butadiene + Ethylene transition structure. They were optimised to a transition state using the Berny method at the semi-empirical AM1 level. Imaginary vibrational frequencies are given below. The exo transition state is 0.68 kcal mol^-1 higher in energy than the endo state.

There is surprisingly little difference in the molecular orbitals between the two forms of the Diels-Alder aduct. The π cloud between the two fragments is a little fuller for the endo form (along the new bonds), but this is only a slight change. Something else must account for the difference in energy. Steric clashes seem the likely answer, a hypothesis supported by Fox, Cardona and Kiwiet.^[3] One end of cyclohexa-1,3-diene is planar, the other is not. The cyclohexa-1,3-diene C_sp³-H groups would clash much more with the anhydride group on the maleic anhydride than with the maleic hydrogens. While the maleic anhydride C=C π cloud is of the right phase to interact with its counterpart on the cyclohexa-1,3-diene, lowering the energy of the transition state, the orbitals on the anhydride part of the molecule are antibonding with respect to this. The exo form reduces the interactions here and potentially allows an orbital interaction between the anhydride orbitals and the small p-like orbitals on the C_sp³.

(This section is a little short, but everything is here Tam10 (talk) 11:24, 14 April 2016 (BST))

Endo form

Exo form

Click here for a dynamic
version of these molecules

Energy / hartrees

-0.05150477

0.05041985