Transition States

The Cope Rearrangement Tutorial

In this section we optimized the the transition states of the [3,3] sigmatropic rearrangement of 1,5-hexadiene. It is know as the cope rearrangement. Firstly we optimized the reactant and products and then investigated the transition states

Optimising Reactants and Products

Firstly we optimized the various conformations of the reactant/products. The result are below. (All calculations done at the HF/321G level of basis set)

Conformer	Symetry	Energy (au) HF/3-21G	File
Gauche 1	C₂	-231.68772	From Script
Gauche 2	C₂	-231.69167	From Script
Gauche 3	C₁	-231.69266122	File:ReactGaucheOPNF.log
Gauche 4	C₂	-231.69153	From Script
Gauche 5	C₁	-231.68962	From Script
Gauche 6	C₁	-231.68916	From Script
Anti 1	C₂	-231.69260	From Script
Anti 2	C_i	-231.69253528	File:Reactanti2NFOP.log
Anti 3	C_2h	-231.68907067	File:ReactantiNF.log
Anti 4	C₁	-231.69097	From Script

We then reoptimized the Anti 2 with a higher Basis set B3YLP/631-G* this file can be found here File:Reactantanti2B3LYPNFOP.log The overall geometry barley changed, however, the energy was reduced by nearly approximately 3 Hartrees. This the higher Basis Set -234.61151569 au compared to -231.69253528 au.

A vibrational analysis was also done File:Anti2VIBNF.log

The first 3 vibration have been visulised below

102cm-1

116cm-1

146cm-1

Spectrum

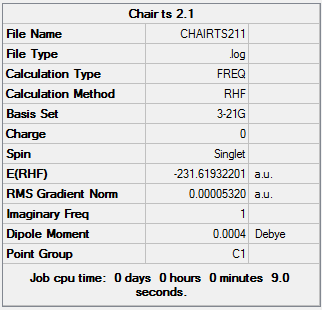
Optimising the chair and boat transition states

We found the chair transition state in two ways, all calculations used HF/321G. The first was to computate a force constant matrix known as the Hessian. The results can be seen below. This method is best used when the TS closely resembles the product.

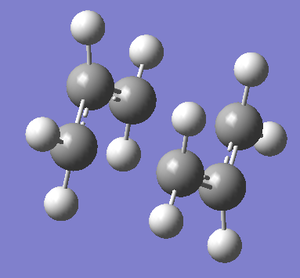
The above animation is for the imaginary vibration -817.7cm-1

However when the TS may differ significantly from the Reactants and products, one has to use the frozen co-ordinates method, which can be seen below. This method allows use to selective optimize parts of the TS whilst others are frozen.

A comparison of the transition bond lengths in interesting because there is a difference between the Hessian and frozen co-ordinates method, with them being 2.02095Å and 2.01992Å respectively.

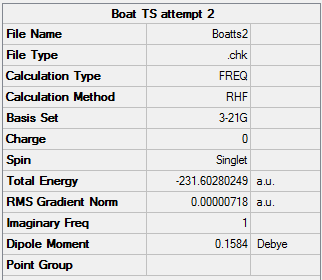
Finding the boat TS proved more tricky, we used the QST2 method. This is where you have an optimized reactant and product and you interpolate between the two to find the transition states.

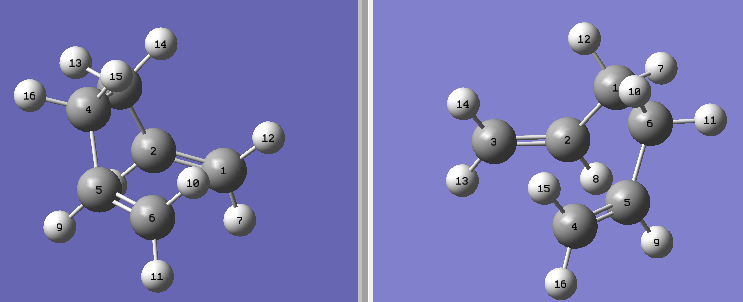
There it can been seen that the carbons are labeled and shows the difference between the reactant and product. Originally for this method we used an anti-conformer, but this did not give us the correct transition state as the computer didnt consider a twist in the bonds. The products and reactants have to resemble the transition state slightly as we are interpolating for us to find the desired transition state.

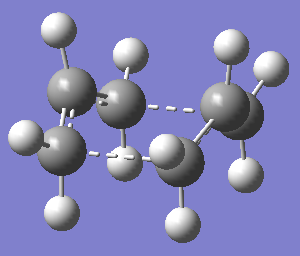
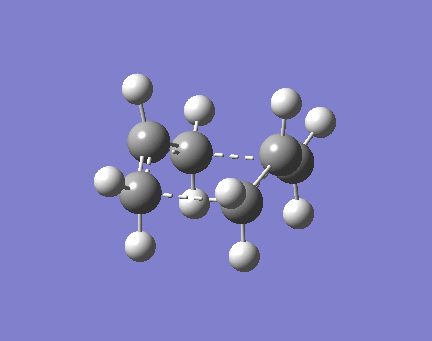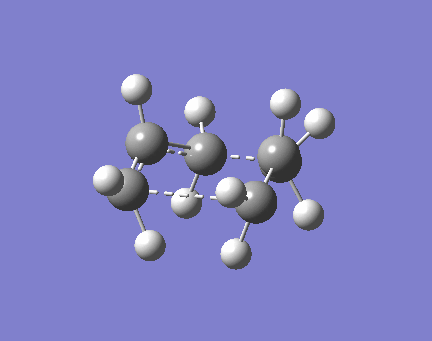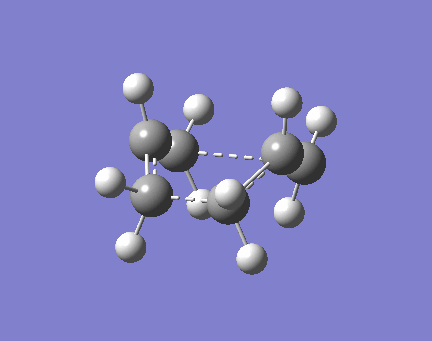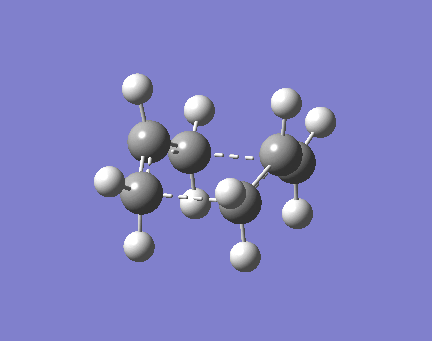
The above imaginary vibration is -840cm-1

The next step was to do an intrinsic reaction co-ordinate calculation of the chair TS structure. As our reaction co-ordinate is symetrical we can afford to only calculate it in one direction.

It was first calculated with 50 steps. and can be see below, starting at the high energy geometry leading the the low energy minimum geometry. To save time in the calculations force constants were calculated only once and not at every step.

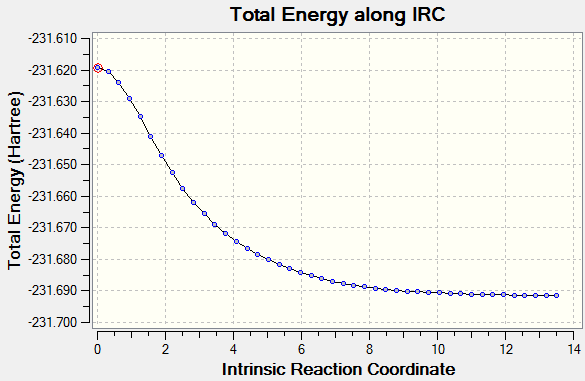
However it was felt that this was not conclusive enough. Therefor the calculation was repeated with 100 steps to make sure the energy had reached minimum.

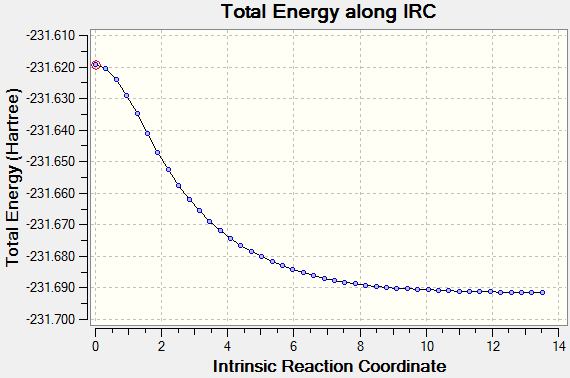
Once the minimum geometry was reached it can be seen that the geometry is of a gauche 3 conformation.

Higher Level Basis Set Comparision

To take things to a higher level of detail we then went on to use a higher level of basis set and compared their energies

B3YLP/631-G*

Structure	Electronic Energies (au)	Sum of electronic and zero-point energies at 0K (au)	Sum of electronic and thermal energies at 298K (au)	Activation Energy
Anti 2	-234.61151569	-234.469161	-234.461979
Chair TS	-234.55698303	-234.414929	-234.409008	0.05168539
Boat TS	-234.54309304	-234.402339	-234.396005	0.06842265

Diels Alder Investigation

The Diels alder reaction is known as a [4s+2s] sigmatropic rearrangement. The primary interactions are pi orbitals, hence 4 pi electrons on the diene, and 2 on the dieneophile. the 's' comes from the symmetry. This is important as the MOs will only be able to interact if the are of the same symmetry, otherwise it is forbidden. This along with the mechanism can bee seen below.

An optimized Molecule of cis-butadiene can be seen below with the HOMO and LUMO illustrated

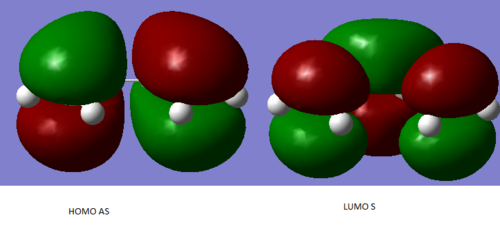
Firstly we are going to investigate the transition state of the diels alder reaction. initially we will investigate the most simple DA reaction which is that between cis - butadiene and ethene. In order to investigate the reaction path way we first optimized the structures of cis - butadiene and ethene. Then in order to find the transition state we did an optimization using the hessian method. A negative vibration of 818cm-1 of observed proving the presence of a transition state. This can be seen in the animation below.

Below is the HOMO of the transition state. The symmetrical nature in the plan of reaction can clearly been seen. Therefor justifying the [4s+2s] assignment given to this reaction.

Regioselectivity in the Diels Alder Reaction

The key files File:EXOHF631GNFDA NEW.LOG File:ENDOHF631GNFDA NEW.LOG

In the next section we will investigate how adding substituents onto the dieneophile changes the regioselectively of the reaction. we will be doing this with cyclohexadiene and maleic anhydride. This can be seen below.

The exo and endo forms come from which way round the maleic anhydride attacks the diene. This can be seen in the TS state animations below.The endo prefix come from when the substituents are underneath the two double bonds of the diene, or inside the ring. The exo prefix comes from the substituents being outside of the 'ring' formed in the TS and not underneath the double bond of the diene. The animation below were calculated at DFT/631G* level of basis set. The exo transition state vibration is at -448cm-1. The endo TS vibration is at -447cm-1.

EXO

ENDO

In this reaction the endo form predominates under kinetic control. We will investigate why this is the case.

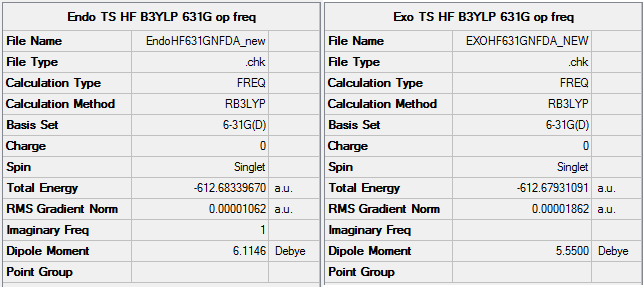
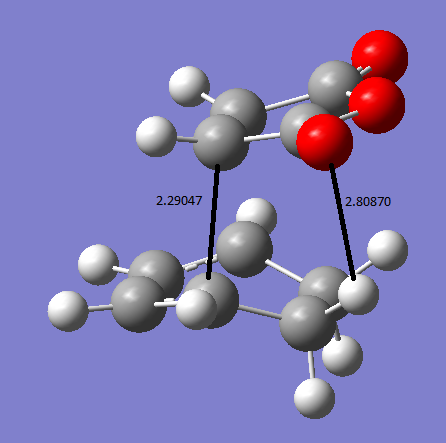
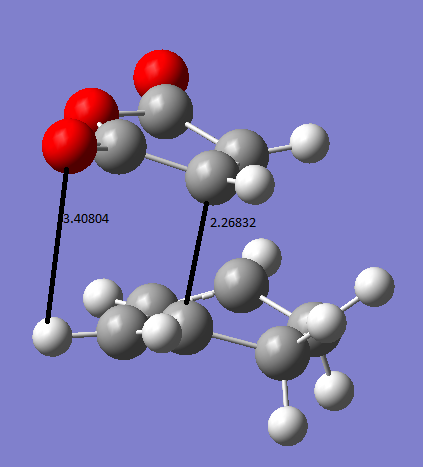
Therefor from he above summary it can be seen that the endo transition state is lower in energy which means under kinetic control it will be formed first. The reason for the exo being higher in energy is that the TS has slightly more steric clashes as if you look on the animation the oxygens are closer to the sp3 hydrogens than in the endo where they are next to the planar sp2 hydrogens . Therefor the Sp3 hydrogen are angled up towards the oxygens on the maleic anhydride and therefor increase the energy of the TS. This can be seen in the diagram below.

However that is not the end of that argument as there has been some evidence of second order orbital overlap effects. we will now investigate the MOs of TSs.

Exo

Endo

An interesting observation here and gives more evidence as to why the exo is higher in energy is the nodal properties around the O=C-O-C=O fragment. Look at the MO for the exo, on this fragment there are 5 nodal points, whereas on the endo there are only 3 in the same region. The number of nodes is proportional to energy, hence why an s orbital is lower in energy than a p orbital. This is known as second order orbital overlap effect. They are known as second order because they don't break or form new bonds in the pericyclic reaction. But their overlap effects energy and that is why the exo is of a higher energy because of decreased overlap and more nodal points.