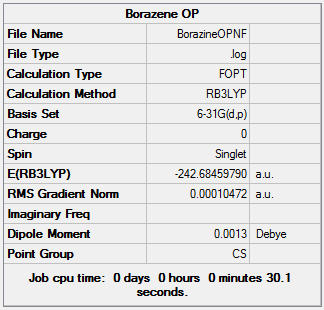
Rep:Mod:NF710M2
Computational Chemistry Module 2
Compulsory Section
Optimization of BH3
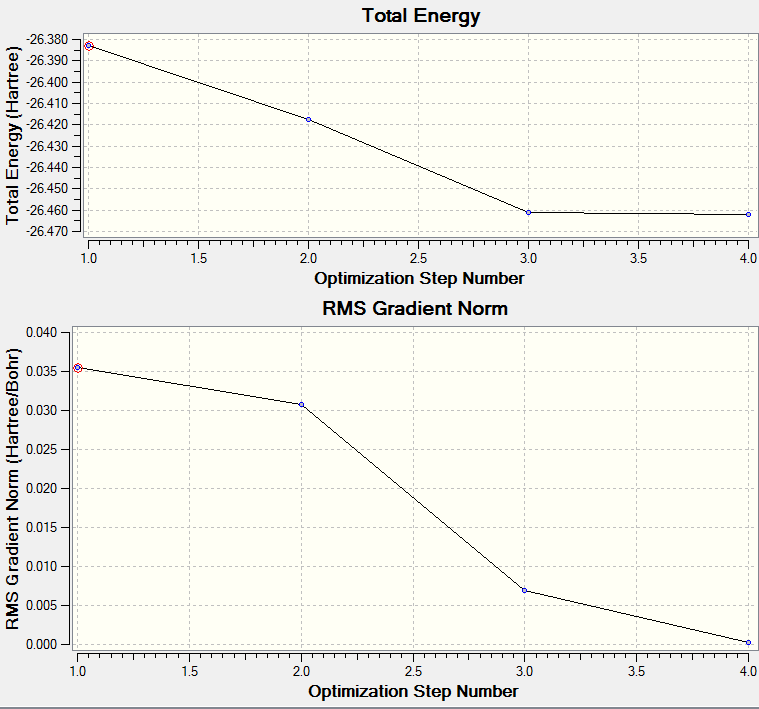
When optimizing BH3 we started with a trigonal planar BH3 with bond lengths 1.5Å which when optimized and at the bottom of the potential energy surface was reduced to 1.19349Å 
| File Name | BH3OPNF |
| File Type | .LOG |
| Calculation Type | FOPT |
| Calculation method | RB3LYP |
| Basis Set | 3-21G |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -26.46226338 a.u. |
| RMS Grad. Norm. | 0.00020662 a.u. |
| Dipole Moment | 0 Debye |
| Point Group | D3H |
| B-H Bond Length | 1.19349Å |
| H-B-H Bond Angle | 120.000° |
| Job Time | 1.0s |
Item Value Threshold Converged?
Maximum Force 0.000413 0.000450 YES
RMS Force 0.000271 0.000300 YES
Maximum Displacement 0.001643 0.001800 YES
RMS Displacement 0.001076 0.001200 YES
Predicted change in Energy=-1.018634D-06
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1935 -DE/DX = 0.0004 !
! R2 R(1,3) 1.1935 -DE/DX = 0.0004 !
! R3 R(1,4) 1.1935 -DE/DX = 0.0004 !
! A1 A(2,1,3) 120.0 -DE/DX = 0.0 !
! A2 A(2,1,4) 120.0 -DE/DX = 0.0 !
! A3 A(3,1,4) 120.0 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
The process was repeated using a better basis set and the bond length was reduced to 1.19202Å
| File Name | BH3OP2 |
| File Type | .LOG |
| Calculation Type | FOPT |
| Calculation method | RB3LYP |
| Basis Set | 6-31+G(d,p) |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -26.61722243 a.u. |
| RMS Grad. Norm. | 0.00021115 a.u. |
| Dipole Moment | 0 Debye |
| Point Group | D3H |
| B-H Bond Length | 1.19202Å |
| H-B-H Bond Angle | 120.000° |
| Job Time | 7.0s |
Item Value Threshold Converged?
Maximum Force 0.000422 0.000450 YES
RMS Force 0.000276 0.000300 YES
Maximum Displacement 0.001672 0.001800 YES
RMS Displacement 0.001095 0.001200 YES
Predicted change in Energy=-1.059107D-06
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.192 -DE/DX = 0.0004 !
! R2 R(1,3) 1.192 -DE/DX = 0.0004 !
! R3 R(1,4) 1.192 -DE/DX = 0.0004 !
! A1 A(2,1,3) 120.0 -DE/DX = 0.0 !
! A2 A(2,1,4) 120.0 -DE/DX = 0.0 !
! A3 A(3,1,4) 120.0 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
With reference to literature The B-H bond length has been reported at 1.190011Å[1] (via infrared spectroscopy) so our value of 1.19202Å isnt too far away. If better basis sets were used im sure we could get closer to this value.
Optimization of TlBr3
An Optimization was performed on the very large TlBr3, to do this we had to use pseudo-potentials and larger basis sets. This is because it takes into account the 186 electrons in this molecule, The potential energy surface can only be modeled to the best of its ability, so we have to use a mixture of basis sets and pseudo potential to take account for this.
DOI:10042/24011 link to d-space
| File Name | TlBr3NFlanL2DZ |
| File Type | .LOG |
| Calculation Type | FOPT |
| Calculation method | RB3LYP |
| Basis Set | LANL2DZ |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -91.21812851 a.u. |
| RMS Grad. Norm. | 0.00000088 a.u. |
| Dipole Moment | 0 Debye |
| Point Group | D3H |
| Tl-Br Bond Length | 2.65095Å |
| Br-Tl-Br Bond Angle | 120.000° |
| Job Time | 19.1s |
Item Value Threshold Converged?
Maximum Force 0.000002 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000016 0.001800 YES
RMS Displacement 0.000010 0.001200 YES
Predicted change in Energy=-4.107348D-11
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 2.651 -DE/DX = 0.0 !
! R2 R(1,3) 2.651 -DE/DX = 0.0 !
! R3 R(1,4) 2.651 -DE/DX = 0.0 !
! A1 A(2,1,3) 120.0 -DE/DX = 0.0 !
! A2 A(2,1,4) 120.0 -DE/DX = 0.0 !
! A3 A(3,1,4) 120.0 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
With refrence to literature using EXAFS spectroscopy the Tl-Br bond length has been noted to be between 2.492 and 2.502Å [2]
Optimization of BBr3
| File Name | BBr3NFGEN |
| File Type | .LOG |
| Calculation Type | FOPT |
| Calculation method | RB3LYP |
| Basis Set | GEN |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -64.43645296 a.u. |
| RMS Grad. Norm. | 0.00000383 a.u. |
| Dipole Moment | 0 Debye |
| Point Group | D3H |
| B-Br Bond Length | 1.93396Å |
| Br-B-Br Bond Angle | 120.000° |
| Job Time | 18.2s |
Item Value Threshold Converged?
Maximum Force 0.000008 0.000450 YES
RMS Force 0.000005 0.000300 YES
Maximum Displacement 0.000046 0.001800 YES
RMS Displacement 0.000030 0.001200 YES
Predicted change in Energy=-5.266345D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.934 -DE/DX = 0.0 !
! R2 R(1,3) 1.934 -DE/DX = 0.0 !
! R3 R(1,4) 1.934 -DE/DX = 0.0 !
! A1 A(2,1,3) 120.0 -DE/DX = 0.0 !
! A2 A(2,1,4) 120.0 -DE/DX = 0.0 !
! A3 A(3,1,4) 120.0 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Bond Length Comparisions
| File Name | BBr3NFGEN |
| File Type | .LOG |
| Calculation Type | FOPT |
Vibrational Analysis of BH3
DOI:10042/24012 link to D space
1 2 3
A2" E' E'
Frequencies -- 1156.1707 1204.2826 1204.2849
Red. masses -- 1.2531 1.1074 1.1074
Frc consts -- 0.9869 0.9463 0.9463
IR Inten -- 93.9187 13.4909 13.4945
Atom AN X Y Z X Y Z X Y Z
1 5 0.00 0.00 0.16 0.00 0.10 0.00 -0.10 0.00 0.00
2 1 0.00 0.00 -0.57 0.00 0.08 0.00 0.81 0.00 0.00
3 1 0.00 0.00 -0.57 0.39 -0.59 0.00 0.14 -0.39 0.00
4 1 0.00 0.00 -0.57 -0.39 -0.59 0.00 0.14 0.39 0.00
4 5 6
A1' E' E'
Frequencies -- 2581.6023 2709.7542 2709.7556
Red. masses -- 1.0078 1.1270 1.1270
Frc consts -- 3.9574 4.8759 4.8759
IR Inten -- 0.0000 142.3127 142.2970
Atom AN X Y Z X Y Z X Y Z
1 5 0.00 0.00 0.00 0.11 0.00 0.00 0.00 0.11 0.00
2 1 0.00 -0.58 0.00 0.02 0.00 0.00 0.00 -0.81 0.00
3 1 0.50 0.29 0.00 -0.60 -0.36 0.00 -0.36 -0.19 0.00
4 1 -0.50 0.29 0.00 -0.60 0.36 0.00 0.36 -0.19 0.00
BH3 Vibrations
| Vibration Number | Vibration Form | Frequency/cm-1 | Intensity | Symmetry |
|---|---|---|---|---|
| 1 | 1156.17 | 93.9187 | a2 | |
| 2 | 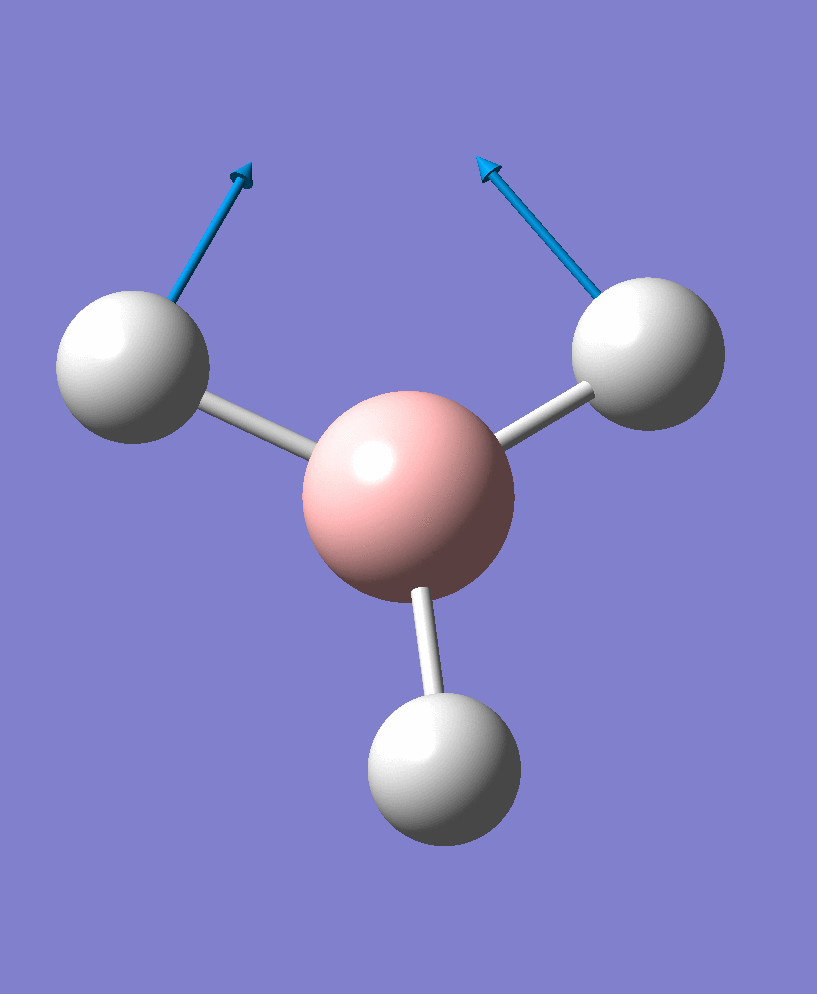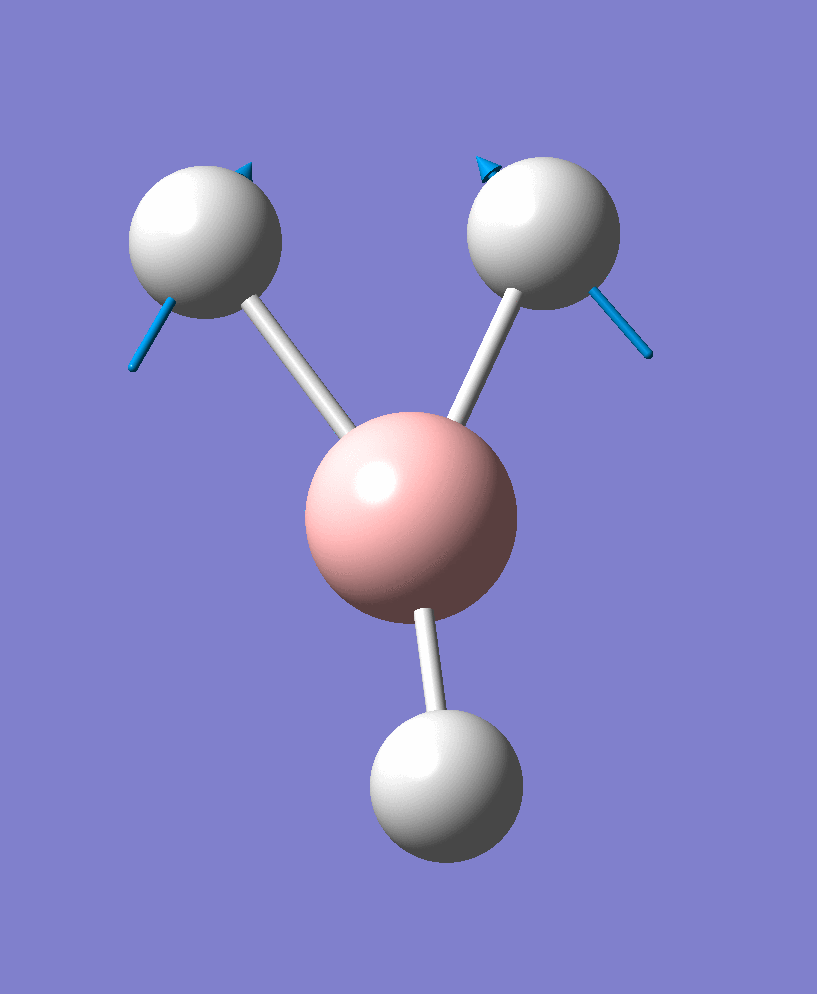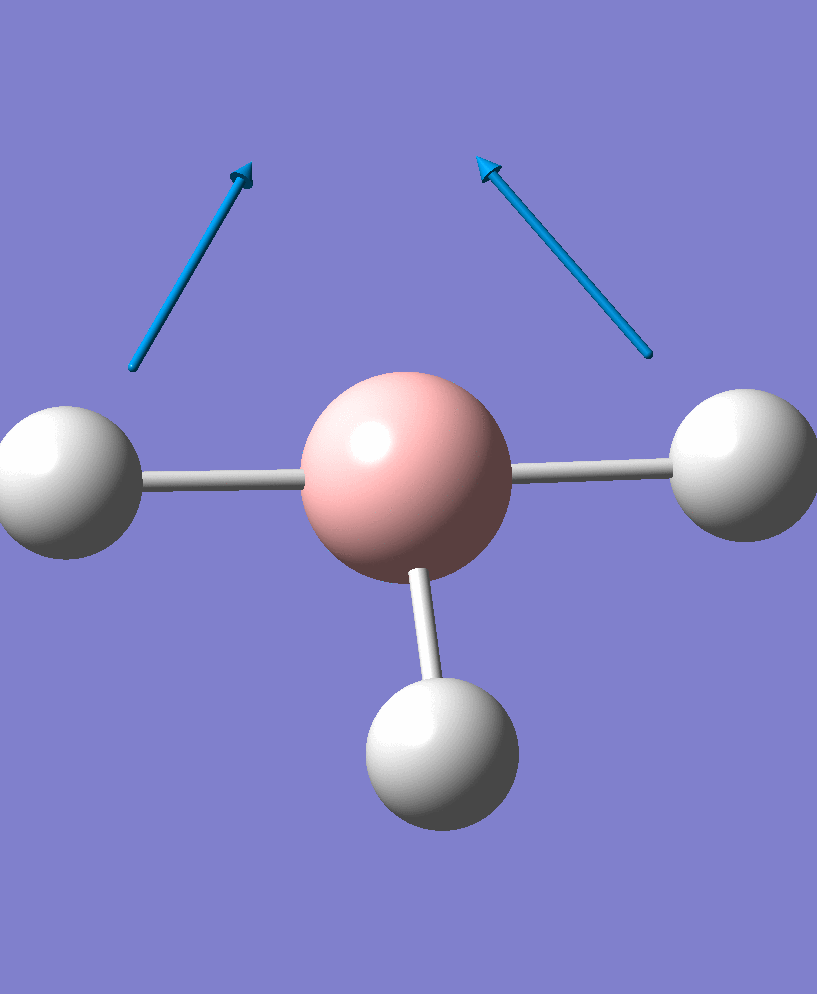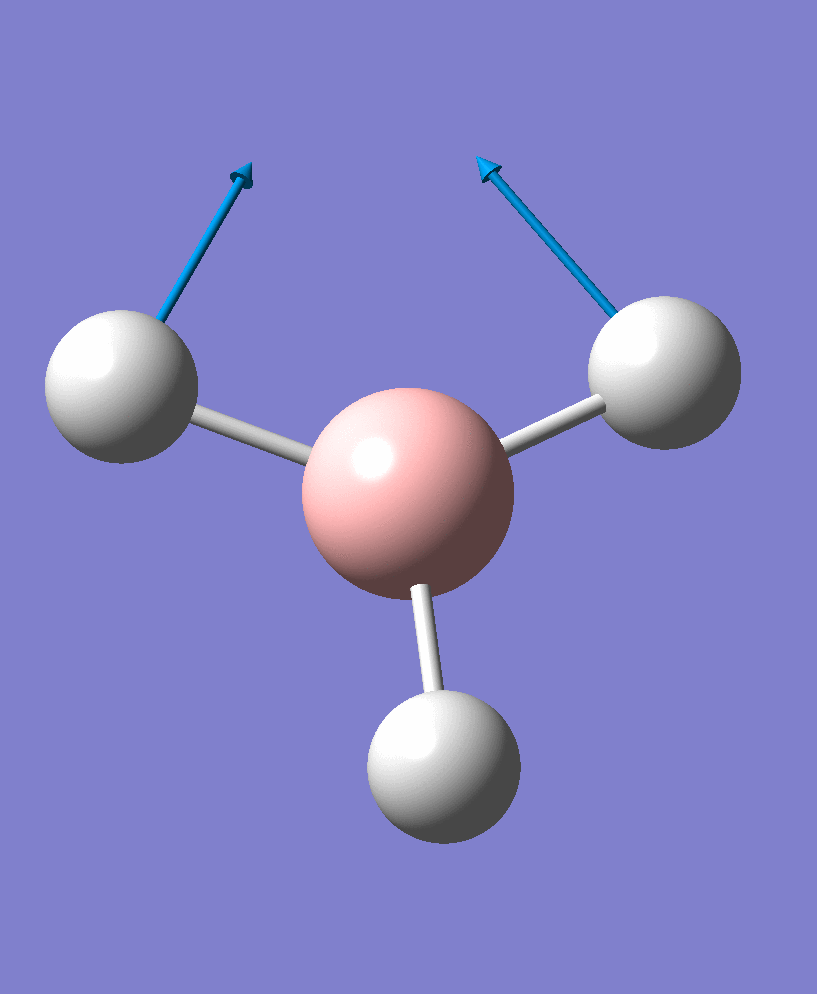 |
1204.28 | 13.4909 | e' |
| 3 | 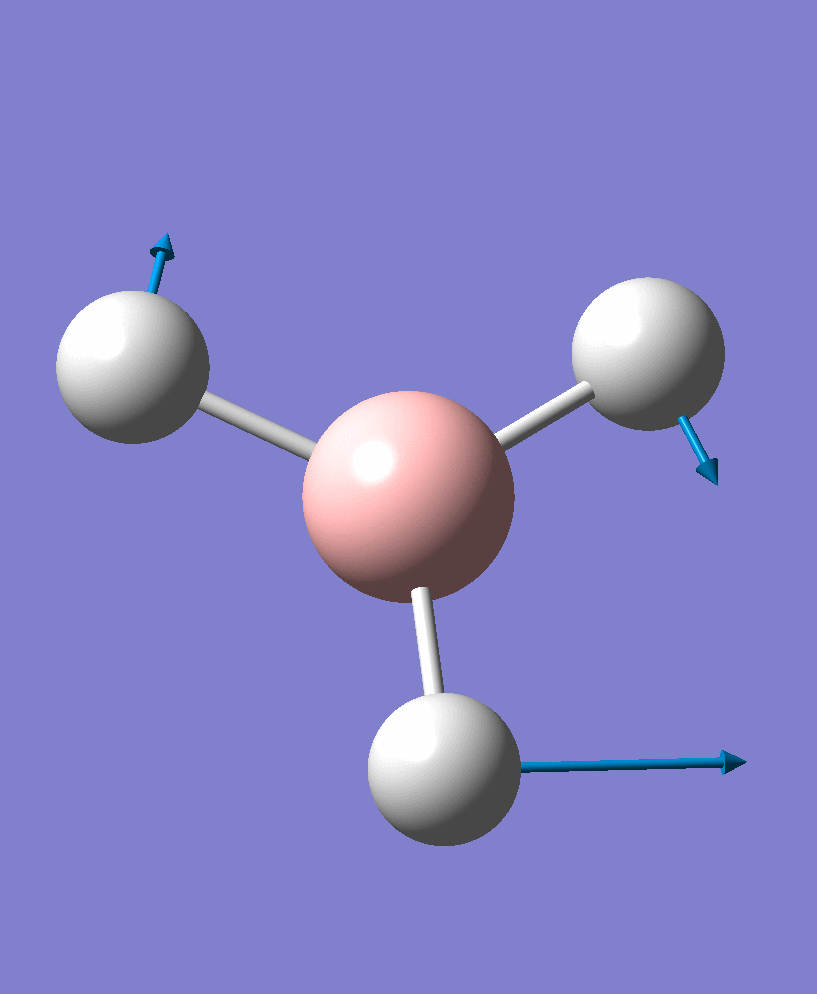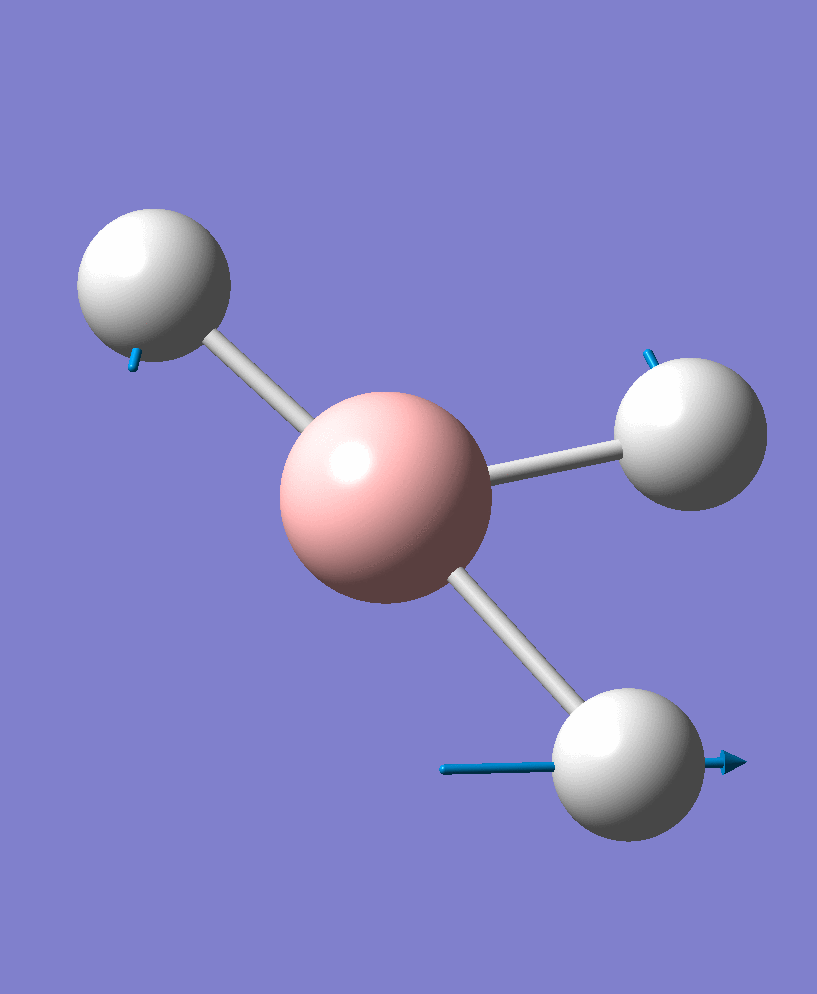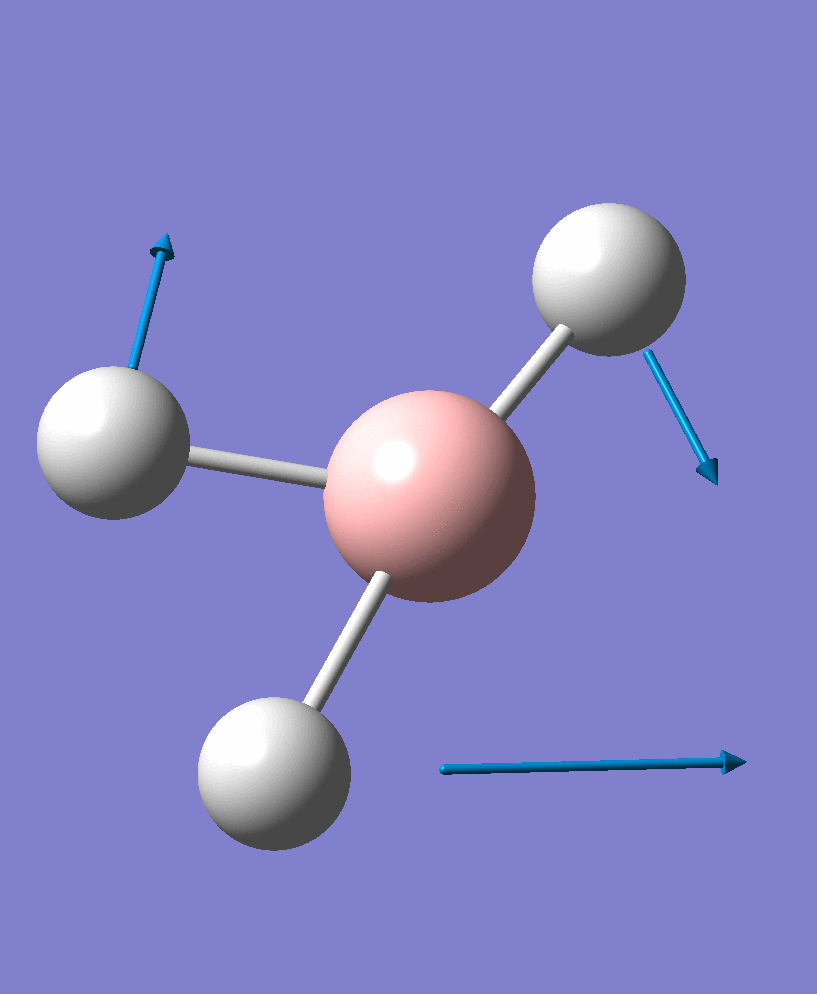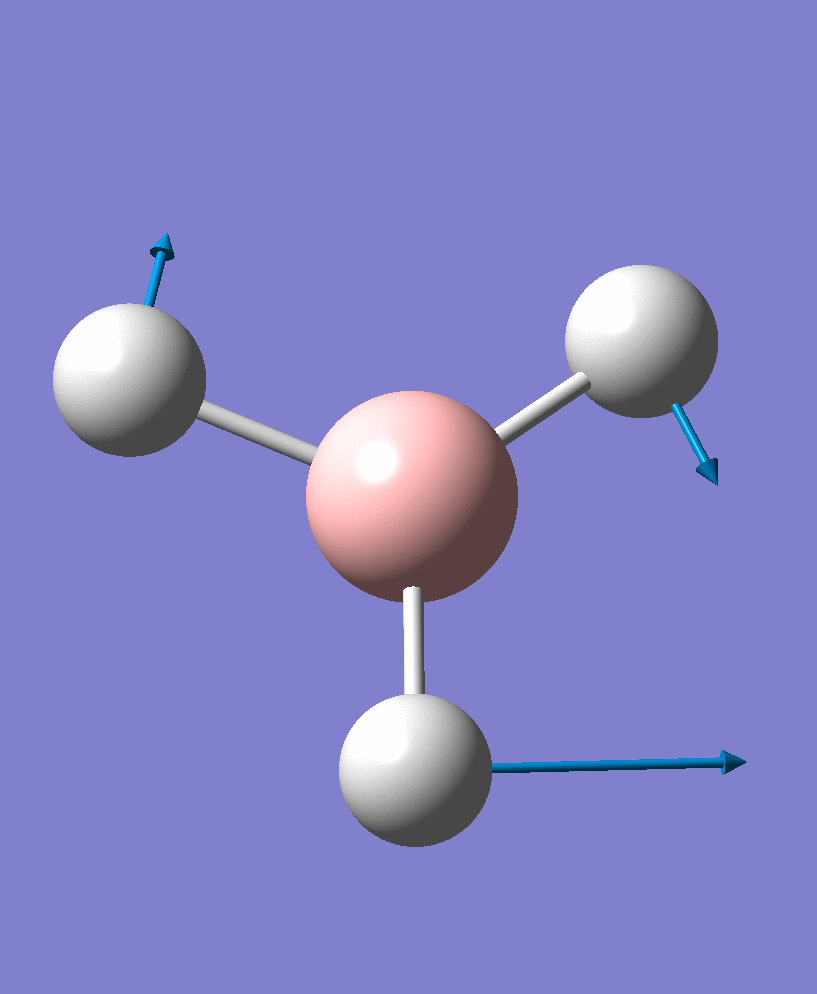 |
1204.28 | 13.4945 | e' |
| 4 |  |
2581.60 | 0 | a1' |
| 5 | 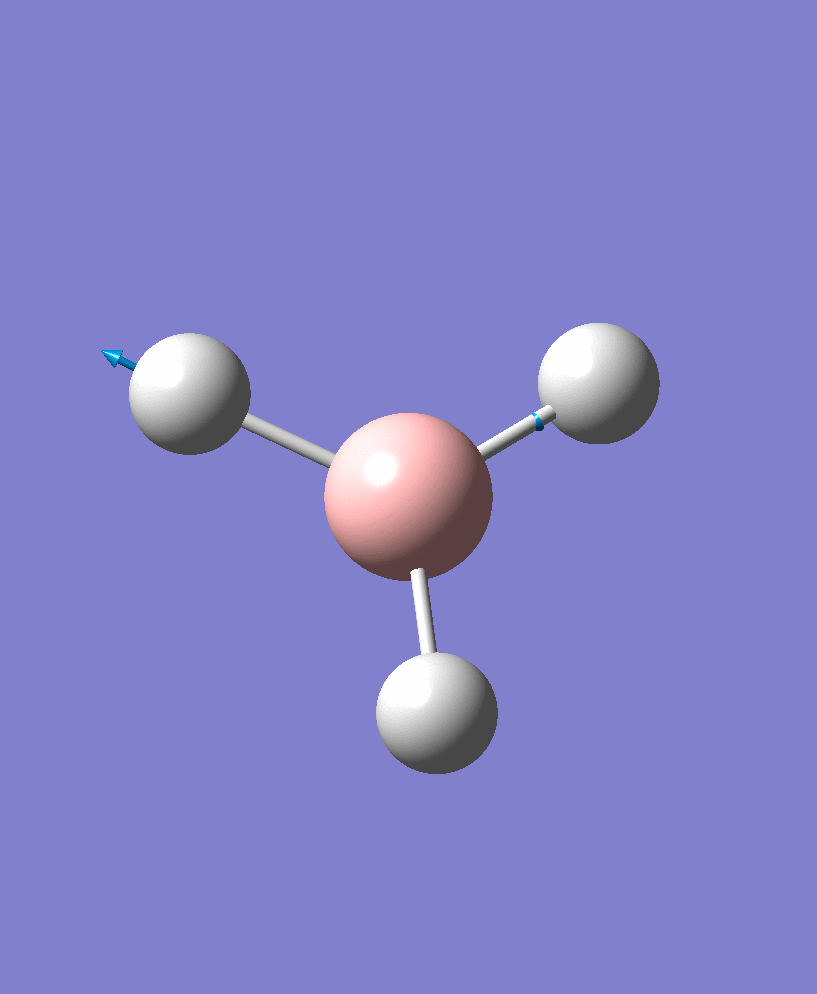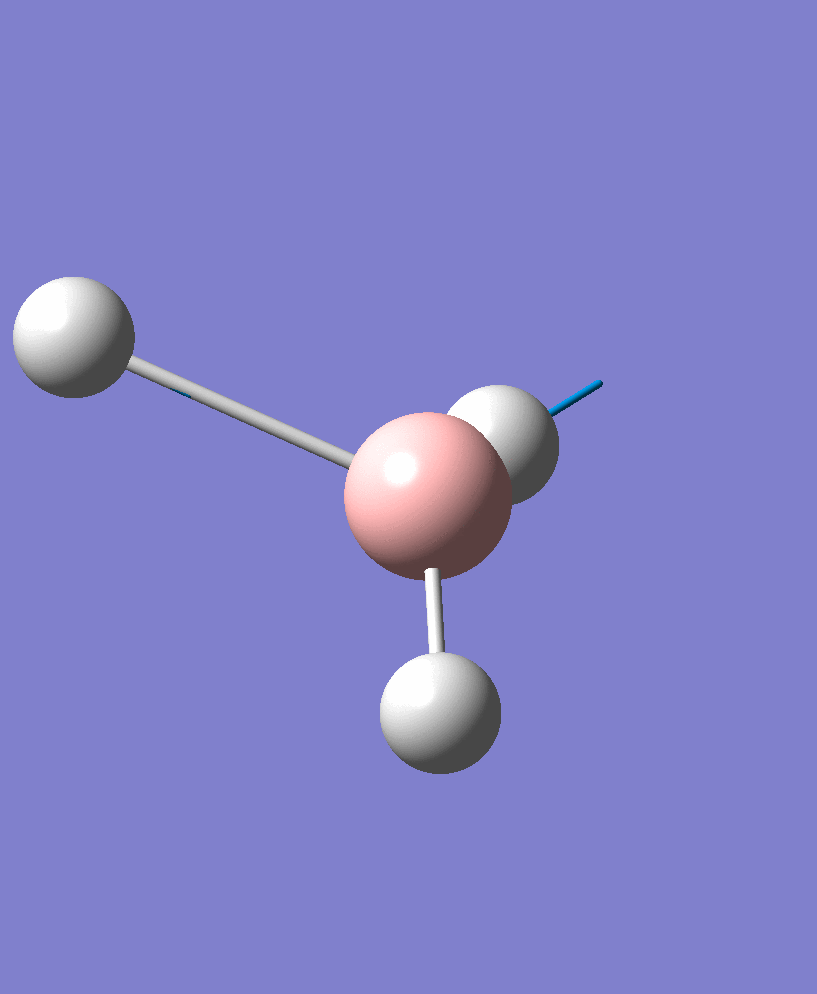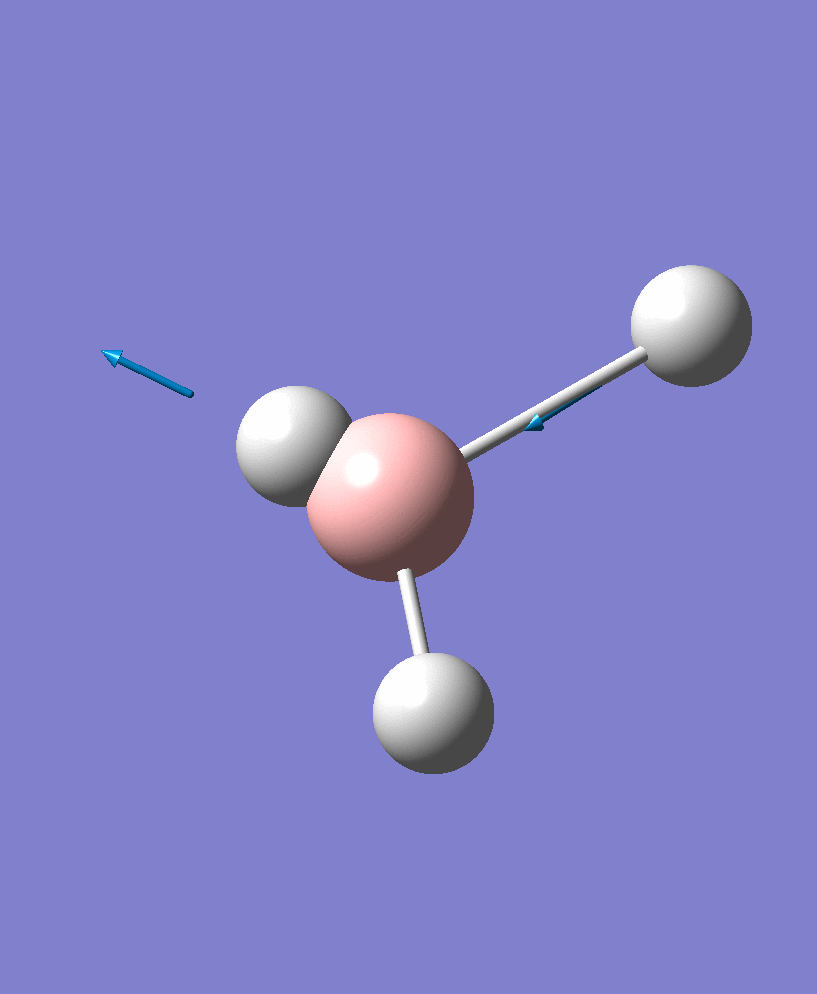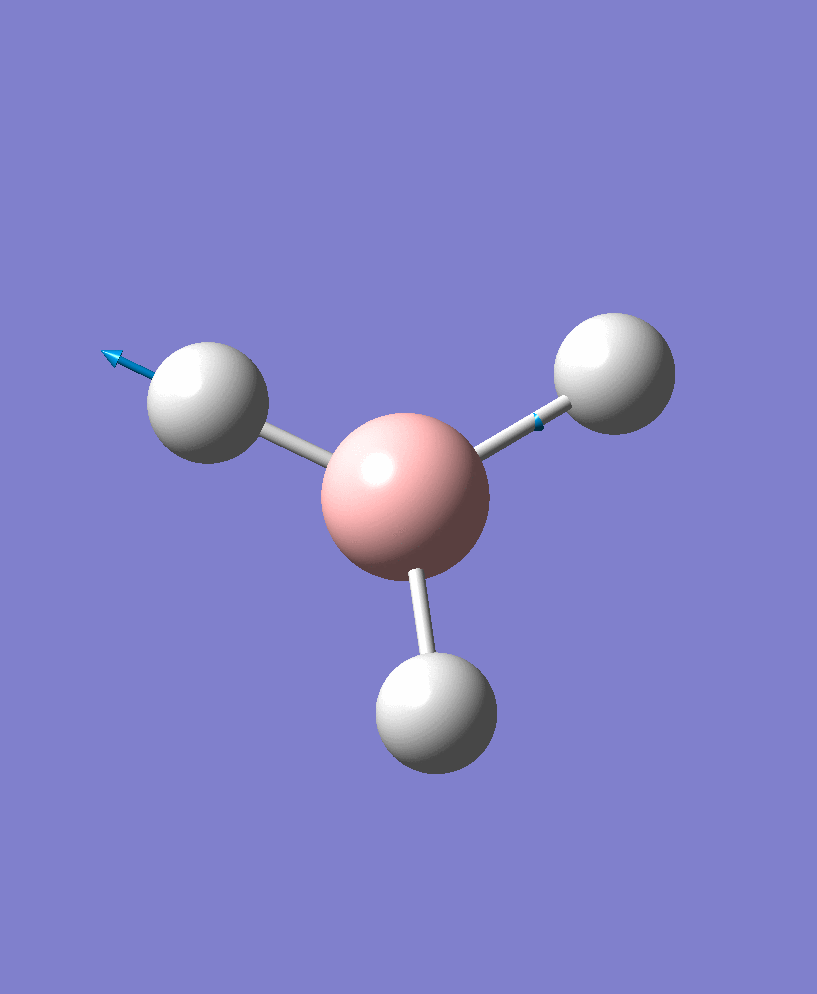 |
2707.75 | 142.3127 | e' |
| 6 |  |
2707.76 | 142.2970 | e' |
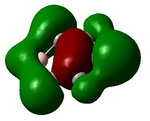
There are 6 vibrational modes, of which only 3 are seen in the spectrum. For a non-linear molecule 3N-6 degrees of freedom, hence this is correct. However the a1' stretch doesnt cause a change in dipole moment which thereformeans it isnt IR active and has an absorbance of 0. However there are two sets of degenerate stretchs so only one peak for each set is observed. Therefor with the A2' this gives us three peaks for A2, E' and another E'.
Vibrational Analysis of TlBr3
TlBr3 Vibrations
1 2 3
E' E' A2"
Frequencies -- 46.4289 46.4292 52.1449
Red. masses -- 88.4613 88.4613 117.7209
Frc consts -- 0.1124 0.1124 0.1886
IR Inten -- 3.6867 3.6867 5.8466
Atom AN X Y Z X Y Z X Y Z
1 81 0.00 0.28 0.00 -0.28 0.00 0.00 0.00 0.00 0.55
2 35 0.00 0.26 0.00 0.74 0.00 0.00 0.00 0.00 -0.48
3 35 0.43 -0.49 0.00 -0.01 -0.43 0.00 0.00 0.00 -0.48
4 35 -0.43 -0.49 0.00 -0.01 0.43 0.00 0.00 0.00 -0.48
4 5 6
A1' E' E'
Frequencies -- 165.2685 210.6948 210.6948
Red. masses -- 78.9183 101.4032 101.4032
Frc consts -- 1.2700 2.6522 2.6522
IR Inten -- 0.0000 25.4830 25.4797
Atom AN X Y Z X Y Z X Y Z
1 81 0.00 0.00 0.00 0.42 0.00 0.00 0.00 0.42 0.00
2 35 0.00 -0.58 0.00 0.01 0.00 0.00 0.00 -0.74 0.00
3 35 0.50 0.29 0.00 -0.55 -0.32 0.00 -0.32 -0.18 0.00
4 35 -0.50 0.29 0.00 -0.55 0.32 0.00 0.32 -0.18 0.00
| Vibration Number | Vibration Form | Frequency/cm-1 | Intensity | Symmetry |
|---|---|---|---|---|
| 1 |  |
46.43 | 3.6867 | e' |
| 2 |  |
46.43 | 3.6867 | e' |
| 3 |  |
52.14 | 5.8466 | a2 |
| 4 |  |
165.27 | 0 | a1' |
| 5 |  |
210.69 | 25.4797 | e' |
| 6 |  |
210.69 | 25.4797 | e' |
Comparison of BH3 and TlBr3 Vibrations
There are no negative vibrations, there proving that they are at a minimum on the potential energy surfaces.
| BH3 Frequency/cm-1 | TlBr3 Frequency/ cm-1 | Symmetry |
|---|---|---|
| 1156 | 52 | A2' |
| 1204 | 46 | E' |
| 2518 | 165 | A1' |
| 2707 | 211 | E' |
The large difference wavenumbers for the same vibrational mode is to do with how the B-H bond is stronger and the reduced mass will be lower. Both leading to a higher frequency. The vibrations have been re-ordered BH3 = A2', E',E', A1', E', E' whereas TlBr3 = E', E', A2', A1', E', E'. the lower energy vibrational modes are bending (movement of the center of mass of the molecule), the higher ones are stretches. You need to use the same potential energy surface to work out the vibrational modes, this was worked out in a previous optimization, for a given basis set, hence you must use the same set.
Frequency analysis is used to make sure we have are at a minimum on the potential energy surface, for example if we obtain negative frequencies we know we are not at a minimum, it can always be used to validate experimental data.
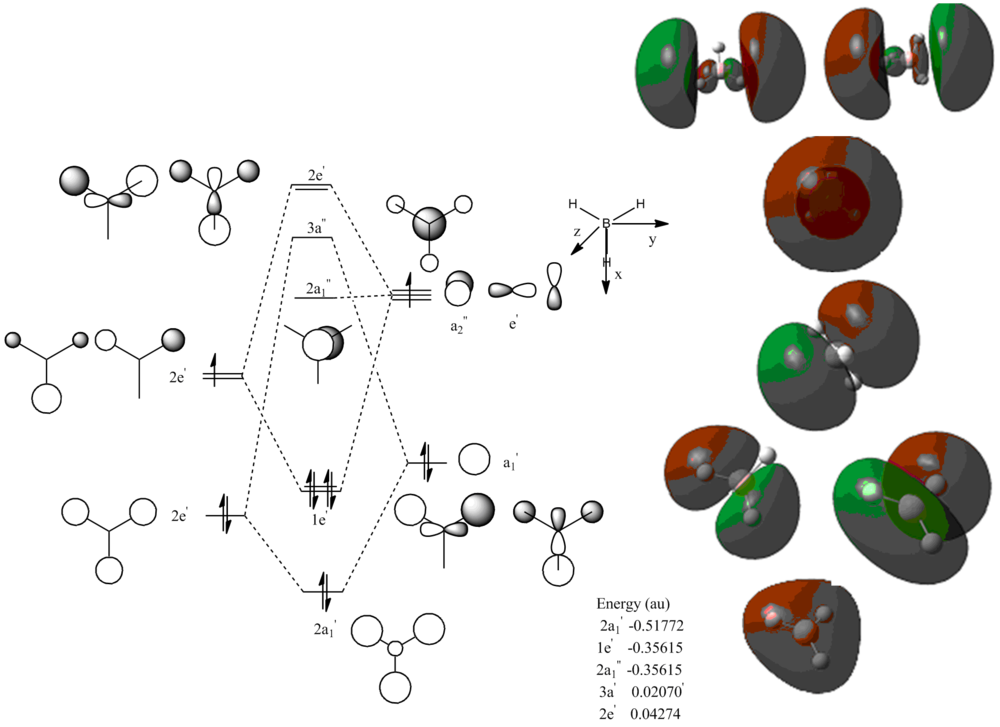
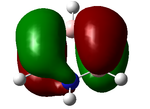
Molecular orbital analysis of BH3
In this next section we shall use the previously optimized BH3 File:BH3OP2.LOG to calculate the molecular orbital of BH3, they are calculated from an energy calculation with the sam basis set as befor.
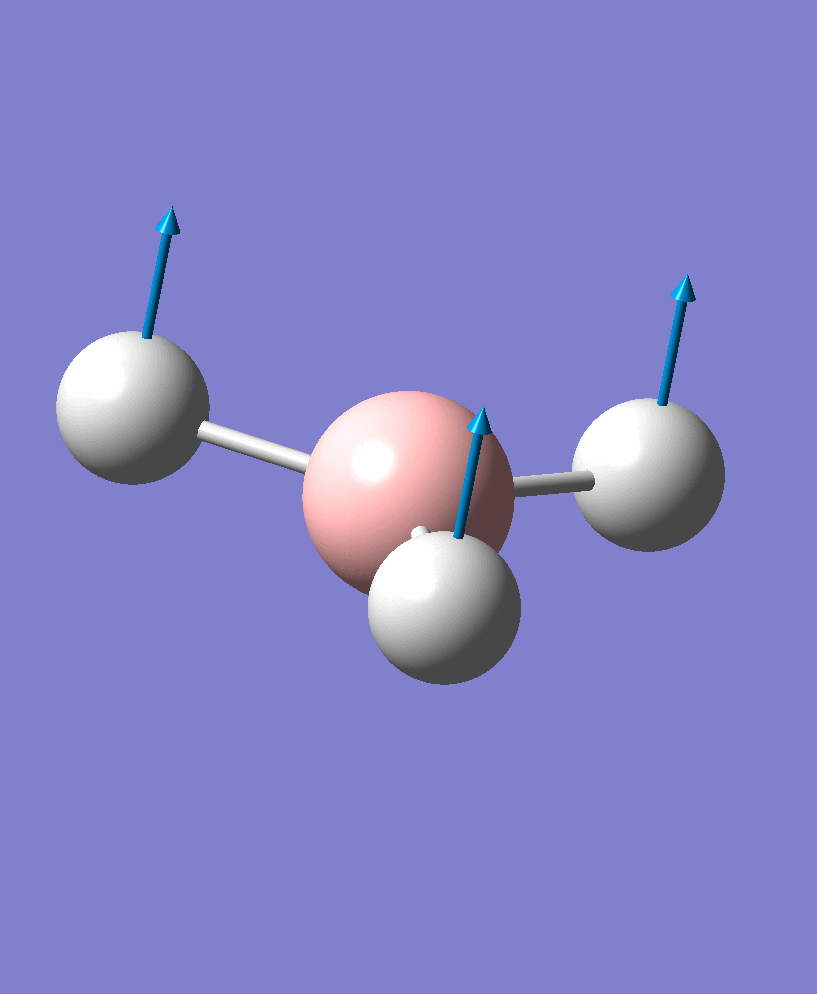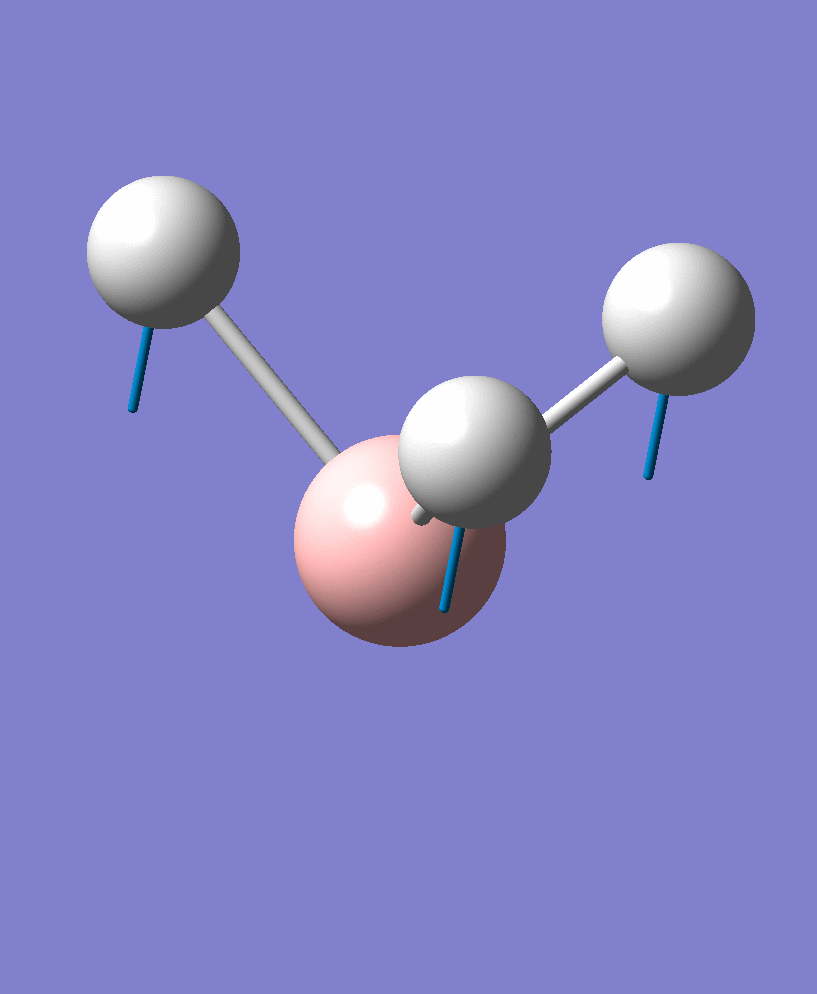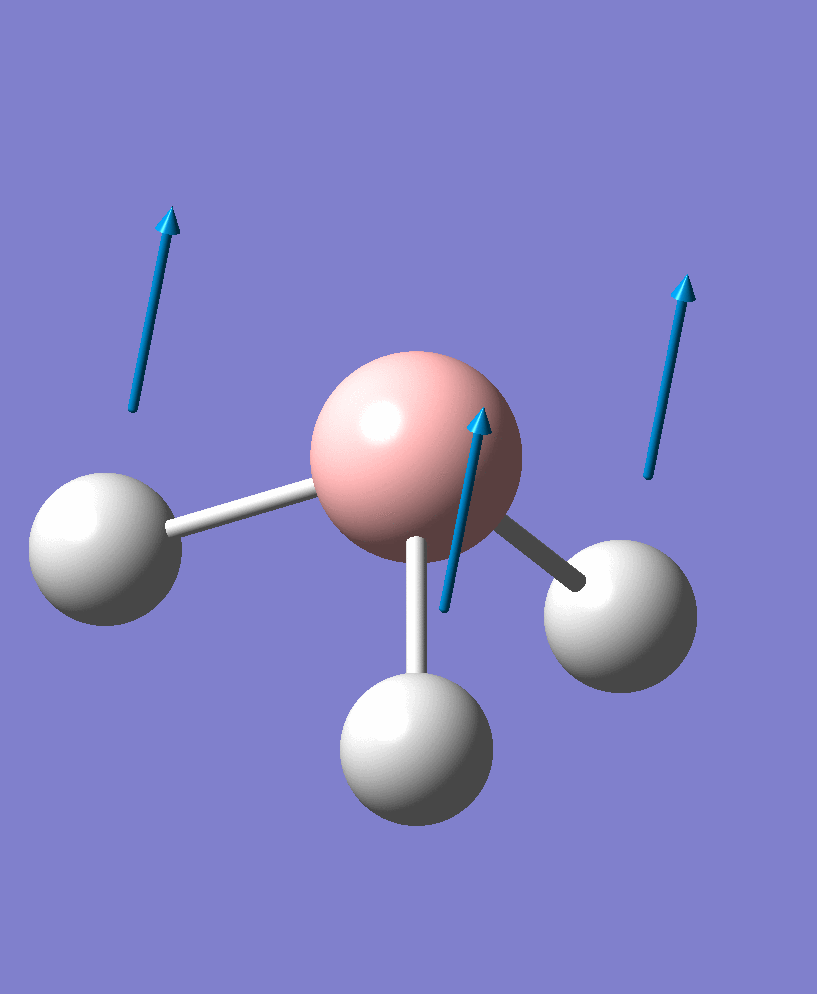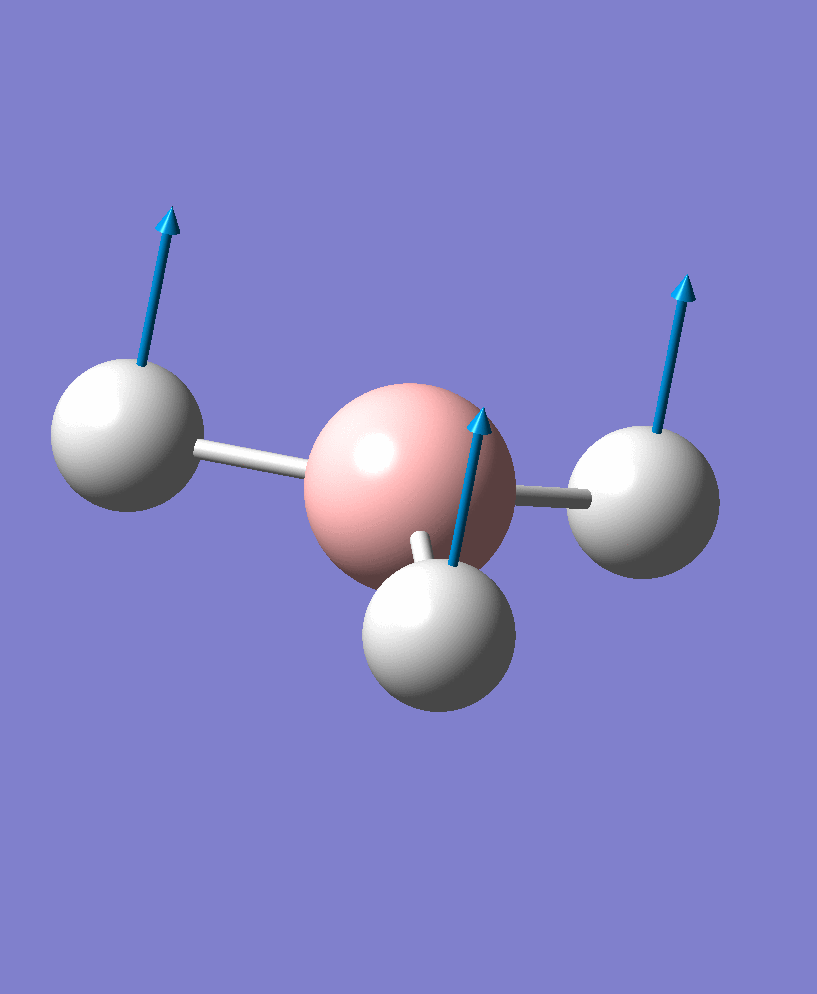
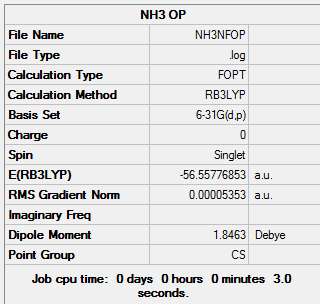
Optimisation and Frequency Analysis of NH3
NH3 was Optimized using Guassian with DFT(B3LYP, 6-31G (d,p) as a basis set) The File is here File:NH3NFOP.LOG
Item Value Threshold Converged?
Maximum Force 0.000102 0.000450 YES RMS Force 0.000062 0.000300 YES Maximum Displacement 0.000300 0.001800 YES RMS Displacement 0.000189 0.001200 YES Predicted change in Energy=-3.515685D-08 Optimization completed. -- Stationary point found.
The process took two optimizations
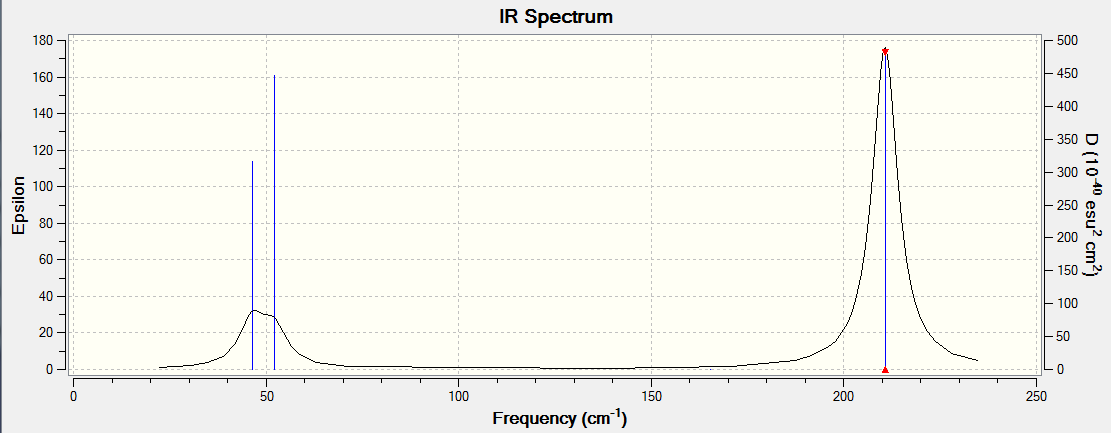
A further Frequency analysis took place to make sure the optimization had reached a minimum the file is here File:NH3NFOPVIB.LOG
1 2 3
A A A Frequencies -- 1089.8696 1694.2609 1694.3007 Red. masses -- 1.1800 1.0645 1.0644 Frc consts -- 0.8258 1.8003 1.8003 IR Inten -- 145.4117 13.5551 13.5500
4 5 6
A A A Frequencies -- 3459.8753 3588.2557 3588.4632 Red. masses -- 1.0272 1.0883 1.0884 Frc consts -- 7.2449 8.2562 8.2573 IR Inten -- 1.0617 0.2730 0.2708
Finally a population analysis took place which can be found here File:NH3NFMO.chk
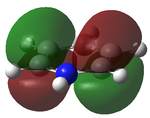
Natural Bond Order (NBO) Analysis of NH3
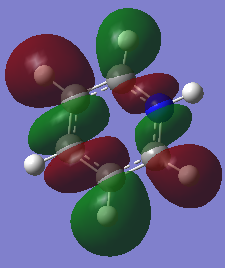
NBO analysis gives us the chance to see where the charges are within in the molecule as can be seen below. It can be done pictorially or numerically as can be seen below.
This shows that the electronegative nitrogen is slightly negatively charged compered to the electropositive hydrogens as it is pulling electron density onto it. If you were to open the .chk file you would be able to vizialize the MOs
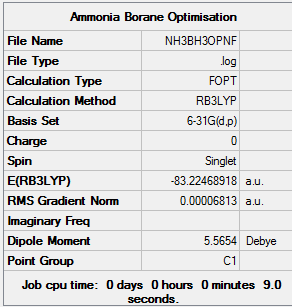
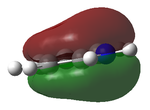
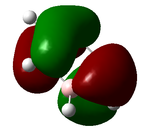
Assoication Energies NH3BH3
Guassian was used to optimize the molecule using DFT (B3LYP, 6-31G(d,p) as a basis set) File:NH3BH3OPNF.LOG
Maximum Force 0.000137 0.000450 YES RMS Force 0.000063 0.000300 YES Maximum Displacement 0.000740 0.001800 YES RMS Displacement 0.000456 0.001200 YES Predicted change in Energy=-2.037459D-07 Optimization completed. -- Stationary point found.
Job Summary
A further frequency analysis took place the file can be found here File:NH3BH3VIBNF.LOG
Low Frequencies - 265.88, 632.38, 639.07, 640.19, 1069.12
| Molecule | Energy |
| BH3 | -26.61722243 a.u. |
| NH3 | -56.55776853 a.u. |
| NH3BH3 | -83.22468918 a.u. |
The disociation energy is calculated from ΔE = E(NH3BH3) - (E(NH3)+(E(BH3))
Therefor:
ΔE = -0.04969822 au = 130.48268655 kJ/mol
This gives a reasonable answer as one would expect an answer in the hundreds of kJ. Stronger bonds have a dissociation of anywhere up to 350 kJ/mol so a weakish B-N at 130 kJ sounds reason able. Literature quotes that the dissociation is 146 - 167 kJ/mol[3], so one would expect if we were to use a better basis set we could perhaps get closer to this value.
Another refrence from literature claims that using microwave spectroscopy a B-N bond length of 1.6576Å[4]
Aromaticity
The most well know aromatic molecule is Benzene, its derivatives are key to life. Aromaticity is known to be present when a cyclic system has 4n + 2 pi electrons, forming a delocalised ring, this is known as Huckle's rule. Aromaticity leads to a stabilizing, lowering in energy which gives some interesting characteristics, such as its tendency to undergo substitution reactions rather than addition reactions like alkenes in other to maintain aromaticity. The delocalisation of its electrons also gives rise to interesting spectroscopic properties for its self and its analogues, as we shall investigate here.
In this section we shall investigate what happens when we replace some of the atoms in the molecule in the ring with elements other than carbon and also whether a borazine containing no carbons can be aromatic.
Optimization and Frequency Calculations
Benzene
Geometry Optimization
Item Value Threshold Converged? Maximum Force 0.000212 0.000450 YES RMS Force 0.000085 0.000300 YES Maximum Displacement 0.000991 0.001800 YES RMS Displacement 0.000315 0.001200 YES Predicted change in Energy=-5.157454D-07 Optimization completed.
-- Stationary point found.
Job Summary
Frequency Calculation DOI:10042/23995
1. 413.80cm-1 0A
2. 414.47cm-1 0A
3. 620.85cm-1 0A
4. 620.94cm-1 0A
5. 693.37cm-1 74.2532A
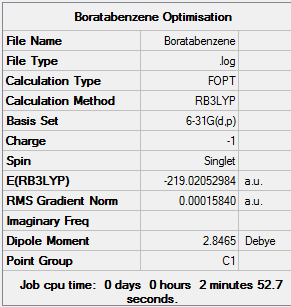
Boratabenzene
Item Value Threshold Converged? Maximum Force 0.000159 0.000450 YES RMS Force 0.000069 0.000300 YES Maximum Displacement 0.000878 0.001800 YES RMS Displacement 0.000326 0.001200 YES Predicted change in Energy=-6.589451D-07 Optimization completed. -- Stationary point found.
Job Summary
Frequency Calculation DOI:10042/24030
Low Frequency Modes
1. 371.35cm-1 2.30A
2. 404.23cm-1 0A
3. 565.25cm-1 0.16A
4. 568.48cm-1 0.09A
5. 607.77cm-1 11.3880A
Pyridinium
Item Value Threshold Converged? Maximum Force 0.000065 0.000450 YES RMS Force 0.000023 0.000300 YES Maximum Displacement 0.000826 0.001800 YES RMS Displacement 0.000176 0.001200 YES Predicted change in Energy=-6.972574D-08 Optimization completed. -- Stationary point found.
Job Summary
Frequency Calculation DOI:10042/24031
Low Frequency Modes
1. 392.46cm-1 0.9649A
2. 404.06cm-1 0A
3. 620.47cm-1 0.0144A
4. 645.25cm-1 0.2819A
5. 676.92cm-1 89.0887A
Borazine
In this Optimization two attempts were needed, hence the small computing time in the second computation.
Item Value Threshold Converged? Maximum Force 0.000234 0.000450 YES RMS Force 0.000067 0.000300 YES Maximum Displacement 0.000931 0.001800 YES RMS Displacement 0.000258 0.001200 YES Predicted change in Energy=-3.563172D-07 Optimization completed. -- Stationary point found.
Job Summary
Frequency Calculation DOI:10042/24029
Low Frequency Modes
1. 288.22cm-1 0.0001A
2. 290.23cm-1 0A
3. 403.76cm-1 23.7774A
4. 525.01cm-1 0.6374A
5. 525.13cm-1 0.6344
Distribution of Charge
In this section we used natural bond order (NBO) analysis to determine the distribution of charge throughout the four molecules. This can be seen in the table below.
| Benzene | Pryidinium ion | Boratabenzene ion | |
|---|---|---|---|
| DOI | DOI:10042/24033 | DOI:10042/24034 | DOI:10042/24035 |
| Pictorial Representation of Charge Distribution | 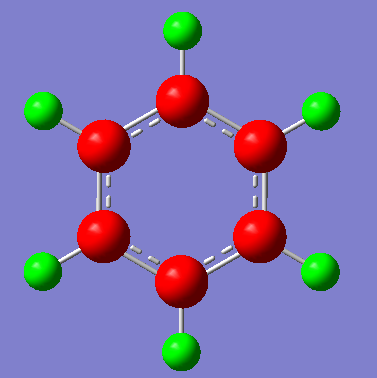 |
 |

|
| Overall Charge | 0 | +1 | -1 |
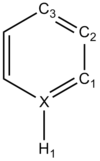
| X = | C | N | B |
| X charge | 0.239 | -0.472 | 0.202 |
| H1 | 0.239 | 0.342 | -0.096 |
| C1 | -0.239 | 0.179 | -0.588 |
| C2 | -0.239 | -0.105 | -0.250 |
| C3 | -0.239 | -0.009 | -0.340 |
| Colour Scaling Relative to charge |
It can bee seen from the above analysis that the three separate molecules exhibit different character because of their differences in electron distribution. In benzene (the molecule that we are referencing) it can be seen that each carbon is the same and so is each hydrogen. The more electron positive hydrogen has a charge of 0.239 and therefor carbon has a charge of -0.239. Giving as expected an even symmetric charge distribution.
The positive pyridinium ion is isolectric to benzene. Formed from the protonation of the base pyridine, one would expect this ion to be acidic and it can be seen that the hydrogen on the nitrogen has a partial positive charge of 0.342 therefor proving its acidity. The electronegativity of the nitrogen causes distortion of the pi cloud, we will discuss this later with reference to the MOs, this distortion can be seen in the charge values of C1.
Boratabenzene is isoelectric to benzene, upon exchange of a BH with a carbon, consiquently it gives a negative charge to the system. Boron is electropositive so the opposite effect of pi cloud distortion is seen here than with pyridinium. This can be seen in the charge values for the ortho and para carbons.
| Borazine | |
|---|---|
| DOI:10042/24036 | |
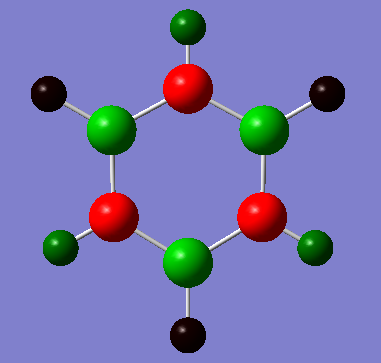
| |
| Atom | Charge |
| N | -0.471 |
| B | 0.307 |
| H(N) | 0.250 |
| H(B) | -0.007 |
| Colour Scaling Relative to charge |
It can bee above that there is an uneven distribution of charge. This is due to the differences in electronegativity, this goes on to explain how the hydrogens on the electronegative nitrogen are acidic and the ones on the electropositive boron are not.
Molecular Orbital Diagram of Benzene
MO orbitals assigned using D6h point group.
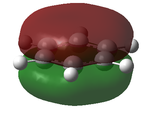
Aromaticity is defined as a delocalised ring of 4n+2 pi electrons in a cyclic molecule. Benzene and the other isoelectric molecules that we are studying, then according to Huckle's rule Benezene must be aromatic. This can be seen in the fifth highest energy occupied molecular orbital as there is a deloclaised pi cloud above and below he plane of the ring made up of the electrons in the pz orbitals. Aromaticity can be know as cyclic delocalisation and we can see this from our calculations. Furthermore it can be seen that the MOs because more diffuse as they become higher in energy and have more antibonding character.
Comparison of Benzene to its Isoelectric Deriviatives
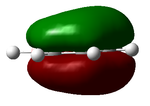
In the maximum bonding pi orbital it can be seen in benzene that there is an even donation of electron density into the orbitals resulting in a highly symmetric molecular orbital. However when we look at boratabenzene we see that there is no longer a high degree of symmetry and the orbital appears to be bulging. This is because the boron is electropositive and therefor contributes less to this bonding orbital. Hence why the MO appears to reduce in size round the boron atom. The opposite is true for pyridinium as the nitrogen is electonegative so we see more contribution to the bonding or orbital and an increase in size of the MO around the nitrogen. This can also be seen when you look at the energies of the orbitals. The difference in electronegativities is over come in borazine by them canceling each other out to give a symmetrical MO of similar energy to Benzene.
In the low energy MO 12 (in Benzene) we see that there a huge difference in energy between the moleles, this is again due to the fact that as the nitrogen is more electronegative it will contribute more to the strongly bonding orbital, lowering its energy. Whereas because the boron barely contributes, giving no stabalisation energy, hence it is a higher energy. In Borazine, you can see how the difference in electronegativities changes the size of the orbitals and their contributions, with the B orbitals very small and the nitrogen ones very large.
For the HOMO orbital we see that when the symmetry of the molecule is broken you lose the degeneracy of the HOMO. The homo also changes energy massively. It can be seen that the two HOMOs from pyridinium and boratabenzene are made up from a different LCAO. This therefor suggests that when the degeneracy is lost, one MO must feel the energy change more greatly. The MO that is not symmetry adapted (ie, the one with 3 pz(+) and 3 pz(-) (which contains the hetro atom) must lower in energy more when the electronegative nitrogen stablises the MO, therefor not being the HOMO anymore. But when the unfavorable electropositive boron destabilizes the MO through lack of contribution, the MO feels it more that the other HOMO (which doesn't contain the hetro atom) and get increased in energy more and become a single HOMO. Hence explaining why the two symmetrical atoms and overall equal charge distribution have a degenerate HOMO and the two with hetro atoms dont.
References
- ↑ Kawaguchi, Kentarou, J. Chem. Phys., 96, 1992, pp3411.
- ↑ Blixt, Johan, J.Am. Chem Soc, 117, 1995, pp5089.
- ↑ J.H. Ren,D.B. Workman and R.R. Squires, J.Am. Chem Soc, 120, 1998, pp10511.
- ↑ Thorne, L. R, J. Chem. Phys, 78, 1983, pp167.