Rep:Mod:NF333
Inorganic Computational Lab
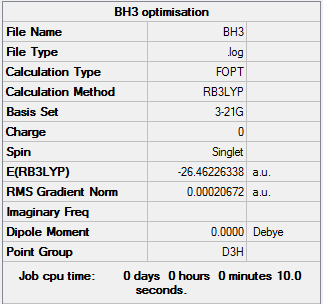
1st Optimisation of BH3
The optimisation file can be found here.
B-H bond distance = 1.19 Å; H-B-H bond angle = 120.0°
Item Value Threshold Converged?
Maximum Force 0.000413 0.000450 YES
RMS Force 0.000271 0.000300 YES
Maximum Displacement 0.001610 0.001800 YES
RMS Displacement 0.001054 0.001200 YES
Predicted change in Energy=-1.071764D-06
Optimization completed.
-- Stationary point found.
2nd Optimisation of BH3
The optimisation file can be found here.
B-H bond distance = 1.19 Å; H-B-H bond angle = 120.0°
Item Value Threshold Converged?
Maximum Force 0.000005 0.000450 YES
RMS Force 0.000003 0.000300 YES
Maximum Displacement 0.000019 0.001800 YES
RMS Displacement 0.000012 0.001200 YES
Predicted change in Energy=-1.305135D-10
Optimization completed.
-- Stationary point found.
Summary and comparison
The total energies of both basis set optimisations:
B3LYP -> -26.46226338 a.u.
631G,dp -> -26.61532363 a.u.
energy difference = 0.15306025 a.u. ≈ 402.79 kJ/mol
Optimisation of GaBr3
The optimisation file can be found here and this is the
Dspace-URL.
Ga-Br bond distance = 2.35 Å; Br-Ga-Br bond angle = 120.0°
The bond length compares well with the literature value of 2.31 Å[1] in Ga2Br4.2(dioxane) or another literature value of 2.57 Å[2].
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000003 0.001800 YES RMS Displacement 0.000002 0.001200 YES Predicted change in Energy=-1.282680D-12 Optimization completed.
Optimisation of BBr3
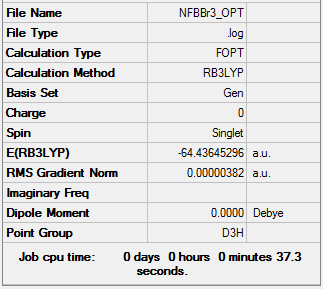
The optimisation file can be found here and this is the
Dspace-URL.
B-Br bond distance = 1.93 Å; Br-B-Br bond angle = 120.0°
Item Value Threshold Converged?
Maximum Force 0.000008 0.000450 YES
RMS Force 0.000005 0.000300 YES
Maximum Displacement 0.000036 0.001800 YES
RMS Displacement 0.000023 0.001200 YES
Predicted change in Energy=-4.027604D-10
Optimization completed.
-- Stationary point found.
Analysis of results
| BH3 | GaBr3 | BBr3 | |
|---|---|---|---|
| bond distance | 1.19 Å | 2.35 Å | 1.93 Å |
Comparing these bond distances with each other it is seen that the ligands as well as the central atom influence their sizes. The bond distance of BBr3 is increased relative to BH3, which is due to the larger atomic size and thus Van-der-Waals radius of Br than that of H. Consequently, the B and Br atoms are further apart from each other and so the bond is longer. However, Br is more electronegative than H reducing the bond distance slightly.
When B is exchanged by Ga as the central atom, the bond distance increases further, for the same reasons as mentioned above. Ga has a greater atomic size and thus a greater Van-der-Waals radius, but a smaller electronegativity than B. Therefore it is further apart from its ligands than B.
Sometimes bonds are not shown in gaussview as it would be expected because they exceed the range of the program, in which it defines that bond. This doesn't mean that there is no bond. It is just not shown. In theory, a bond consists of one or more pairs of electrons that are shared between two nuclei. Line(s) is put in between just for visualisation.
Frequency analysis of BH3
The frequency analysis file can be found here.
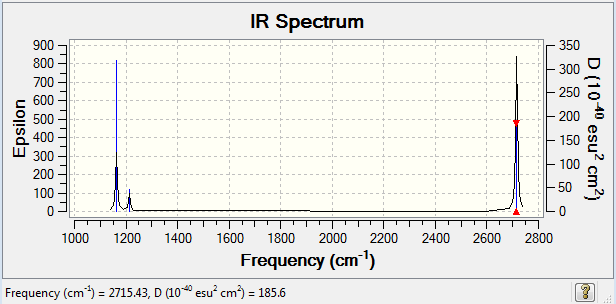
Low frequencies --- -0.9033 -0.7343 -0.0055 6.7375 12.2491 12.2824 Low frequencies --- 1163.0003 1213.1853 1213.1880
Only three peaks are seen rather than six (corresponding to the number of vibration modes) because as shown in the table below one of the modes has 0.0 intensity, thus is not seen as it is IR inactive (no change in dipole moment). Two other pairs are degenerate, so two peaks stand for four vibration modes. Ergo 6 - 3 = 3 peaks.
| no. | form of the vibration | frequency/cm-1 | intensity | symmetry: D3h point group |
|---|---|---|---|---|
| 1 |  The H atoms move up and down together in a concerned motion, always staying in the same plane. The B atom moves more slowly into the opposite direction. |
1163 | 92 | A2" |
| 2 |  While one H atom is slowly going up and down with the B atom, the two other H atoms are moving down towards a line that can be imagined as an elongation of the "stationary" H's bond, and up towards a line perpendicular to the previous. |
1213 | 14 | E' |
| 3 |  This is the same vibration as 2, however, the last H atom is pendulate, too - from left to right over the imagined light (elongation of its bond if stationary). |
1213 | 14 | E' |
| 4 |  All H atoms move in towards the central atom and out away from the central atom together in a concerted motion, the B atom is stationary. |
2582 | 0 | A1' |
| 5 |  Two H atoms stretch asymmetrically, while the third is fixed to the B atom, that moves towards the approaching H atom. |
2715 | 126 | E' |
| 6 |  Two H atoms stretch symmetrically, while the third H atom stretched asymmetrically to the other two. The B atom is moving back and forth symmetrically to the third H atom. |
2715 | 126 | E' |
Frequency analysis of GaBr3
The frequency analysis file can be found here and this is the Dspace-URL.
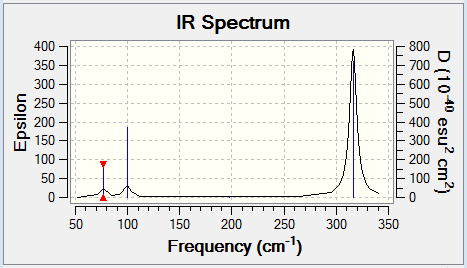
Low frequencies --- -0.5252 -0.5247 -0.0024 -0.0010 0.0235 1.2010 Low frequencies --- 76.3744 76.3753 99.6982
| no. | form of the vibration | frequency/cm-1 | intensity | symmetry: D3h point group |
|---|---|---|---|---|
| 1 |  |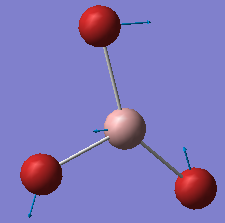
76 | 3 | E' |
| 2 |  |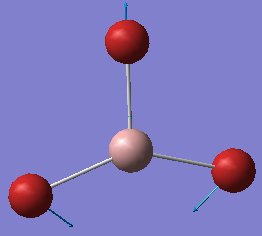
76 | 3 | E' |
| 3 |  |
99 | 9 | A2" |
| 4 |  |
197 | 0 | A1' |
| 5 |  |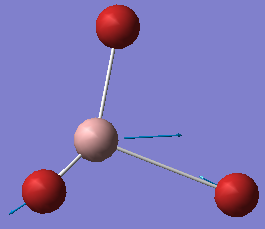
316 | 57 | E' |
| 6 |  |
316 | 57 | E' |
| Frequency, corresponding Intensity | Point group | ||
|---|---|---|---|
| BH3 | GaBr3 | BH3 | GaBr3 |
| 1163, 92 | 76, 3 | A2" | E' |
| 1213, 14 | 76, 3 | E' | E' |
| 1213, 14 | 99, 9 | E' | A2" |
| 2582, 0 | 197, 0 | A1' | A1' |
| 2715, 126 | 316, 57 | E' | E' |
| 2715, 126 | 316, 57 | E' | E' |
Frequency is directly proportional to the energy (E = hv). The large frequency values of BH3 thus indicate that BH3 vibrates at higher energy. This means that more energy is need for borane to stretch or bend. This could be reasoned by the fact that the Ga atom and Br atoms in GaBr3 are bigger in size and contain much more electrons than the B atom and H atoms in borane do, which obviously leads to greater repulsion and a longer bond length easing up vibration.
Looking at the equation below, also shows that molecules of greater size have lower frequencies thus lower energies. Clearly, GaBr3 has a bigger mass than borane does.
[3]
The IR spectra look very similar with both having 3 peaks of similar relative hights. The only differences are that the peaks of borane have intensities and that the peaks of GaBr3 are broader probably because GaBr3's degenerate frequencies are slightly more different than boranes.
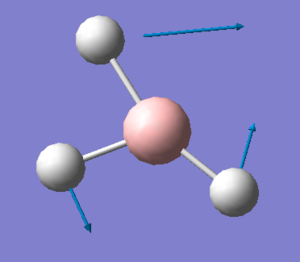
The first and the third mode have swapped places for GaBr3 compared to BH3. Looking at the third vibration mode of GaBr3 it becomes clear why this is like that. This is the mode that requires borane the least energy while it does the third least for GaBr3 as already stated. The mode restricts all Br atoms to stay in the same plane and vibrate horizontally from above to below the central Ga atom and vice versa. As Br atoms have a much greater size and more electrons than H atoms there is more friction and electron-electron repulsion between the Br atoms than there is for the H atoms. Thus the reordering of modes.
Following on from that A2" and E' lie closely together in energy while A1' and E' do the same, though with higher in energy. This is due to the fact that the last three modes of each molecule involve stretching and shortening of the B-H / Ga-Br bonds, which required a lot of energy or leads to great repulsion.
In contrast, the other three modes involve the motion around the central atom rather than closer or further away from it i.e. the bond length mostly stays the same for these.
The same basis set as well as the same method needed to be chosen for any optimisation and frequency calculation in order to have the molecules on exactly the same level and thus be able to compare them.
Frequency analysis are performed to check that a minimum structure of the molecule has been obtained. It is known that every molecule has 3N-6 vibrational frequencies. The essential information are the "low frequency" details given in the log file, which are the "-6 frequencies". The closer to zero these zero frequencies are the more accurate and precise the method is that has been used. Usually only values below 15 cm-1 are of acceptable accuracy.
Molecular Orbitals of BH3
The frequency analysis file can be found here and this is the Dspace-URL.
The computed MOs do agree with the qualitative one. However, often there are major differences due to the inaccuracy in drawing the actual electron density. This already starts with the second a1' orbital. While the computed MO pictures the whole molecule are to be encovered in electron density, by hand only a rough estimate (and the most likely abundance) of the electron density of the molecule is shown. In return, the qualitative approach accounts for the fact, which atom has a larger contribution to bonding/antibonding in for this particular MO, while the computed does not.
Therefore, in general, it can be said that the qualitative approach's precision should be handled with care. But it sure is very useful and fulfills its purpose of illustrating the individual MOs, their interactions and relative energies.
NBO analysis of NH3
Optimisation of NH3
The optimisation file can be found here.
Item Value Threshold Converged?
Maximum Force 0.000024 0.000450 YES
RMS Force 0.000012 0.000300 YES
Maximum Displacement 0.000079 0.001800 YES
RMS Displacement 0.000053 0.001200 YES
Predicted change in Energy=-1.629715D-09
Optimization completed.
-- Stationary point found.
Frequency of NH3
The frequency analysis file can be found here.
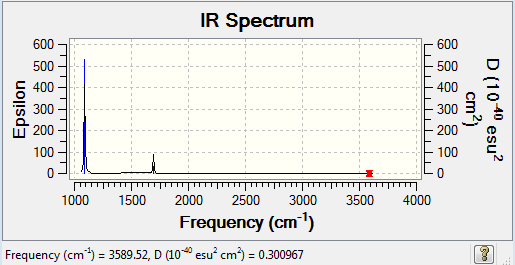
Low frequencies --- -30.7764 -0.0011 0.0016 0.0018 20.3142 28.2484 Low frequencies --- 1089.5557 1694.1237 1694.1868
Natural Bond Orbital Analysis of NH3
The population analysis file can be found here.
| Charge Distribution of NH3 | Specific NBO charges for N and H |
|---|---|
 Bright red colour indicates negative charge, |
 NBO charge of N atom = -1.125 |
As can be seen nitrogen is more negatively charged. This is because it has a greater electronegativity than hydrogen and can effectively withdraw electron density from these due to a good orbital overlap.
Association energy of ammonia borane
Optimisation of NH3BH3
The optimisation file can be found here.
Item Value Threshold Converged?
Maximum Force 0.000121 0.000450 YES
RMS Force 0.000057 0.000300 YES
Maximum Displacement 0.000508 0.001800 YES
RMS Displacement 0.000294 0.001200 YES
Predicted change in Energy=-1.611643D-07
Optimization completed.
-- Stationary point found.
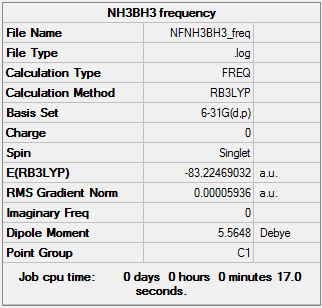
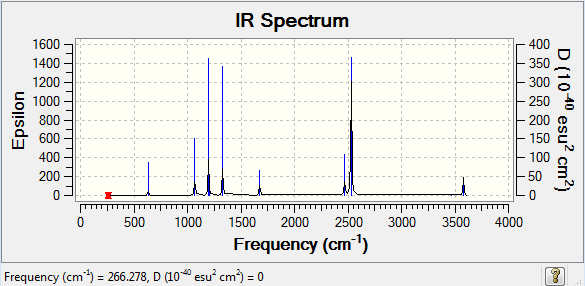
Frequency of NH3BH3
The frequency analysis file can be found here.
Low frequencies --- -0.0014 -0.0012 -0.0010 18.5340 23.7773 41.0318 Low frequencies --- 266.2868 632.2307 639.8263
Energies of ammonia, borane and ammonia borane
E(BH3) = -26.61532363 a.u.
E(NH3) = -56.55776856 a.u.
E(NH3BH3) = -83.22469032 a.u.
ΔE = E(NH3BH3) - [E(NH3) + E(BH3)] = -0.05159813 a.u.
Since "0.01 kJ/mol = 0.0000038 a.u.", the association energy = -135.78 kJ/mol
First of all this is a sensible value as it has a negative value indicating that energy is givven off upon the formation of the bond. Secondly association energies are generally in the range of 100 to few hundreds of kJ/mol.
