Jump to content

Rep:Mod:Mywiki

From ChemWiki

Ammonia

Calculations were carried out using the programme "Gaussian".

Summary of Results

Calculation method: RB3LYP
Basis Set: 6-31G(d,p)
Final Energy E(RB3LYP): -56.55776873 a.u.
RMS Gradient Norm: 0.00000485 a.u.
Point Group: C3V


Item Table from log file

Item               Value     Threshold  Converged?
 Maximum Force            0.000004     0.000450     YES
 RMS     Force            0.000004     0.000300     YES
 Maximum Displacement     0.000072     0.001800     YES
 RMS     Displacement     0.000035     0.001200     YES

It can be seen that all the items have converged. This shows that the optimisation of the molecule was successful.

Bond angle and Bond Length

The H-N-H bond angle is 105.74115 degrees. The N-H bond length is 1.01798 Angstrom.

Ammonia molecule

View the log file here: File:MALA NH3 OPTF POP.LOG

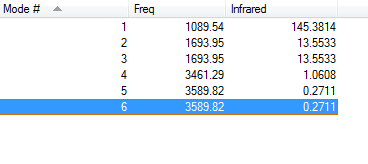
Vibrations of NH3 molecule in IR spectrum

From the 3N-6 rule, 3 vibrational modes are expected. Modes 2 and 3 (1693.95 cm-1), and 5 and 6 (3589.82 cm-1) are degenerate. Modes 1 and 2(or 3) are bending vibrations, while Modes 4 and 5 (or 6) are stretching vibrations. Mode 4 is highly symmetric (as the dipole doesn't change) Mode 1 is the "umbrella" mode. 3 bands would be expected to show up in an experimental spectrum of gaseous ammonia.

Since Nitrogen is more electronegative than Hydrogen, you'd expect N to have a negative charge, and H to have a positive charge. This is confirmed by the calculations which give N having a charge of -1.125 and H 0.375.

Nitrogen

Summary of Results

Calculation method: RB3LYP
Basis Set: 6-31G(d,p)
Final Energy E(RB3LYP): -109.52412868 a.u.
RMS Gradient Norm: 0.00000365 a.u.
Point Group: D∞H


Item Table from log file


         Item               Value     Threshold  Converged?
 Maximum Force            0.000006     0.000450     YES
 RMS     Force            0.000006     0.000300     YES
 Maximum Displacement     0.000002     0.001800     YES
 RMS     Displacement     0.000003     0.001200     YES
Nitrogen molecule


View the log file here: File:MALA N2 OPTF POP.LOG

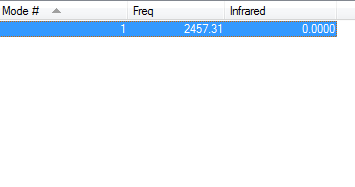
Vibrations of N2 in IR spectrum

For linear molecules, the 3N-5 rule is followed. This predicts the number of vibrational modes in nitrogen to be 1- which is in agreement with our calculation. There is one stretching vibration at 2457.31 cm-1. However, this does not show up in the infrared spectrum as N-N has no net dipole moment.

Bond Length

The bond length of Nitrogen is 1.10550 Angstrom.


Hydrogen

Summary of Results

Calculation method: RB3LYP
Basis Set: 6-31G(d,p)
Final Energy E(RB3LYP): -1.17853936 a.u.
RMS Gradient Norm: 0.00000017 a.u.
Point Group: D∞H


Item Table from log file

 Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000450     YES
 RMS     Force            0.000000     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000001     0.001200     YES


Hydrogen molecule


View the log file here: File:H2 mp.LOG

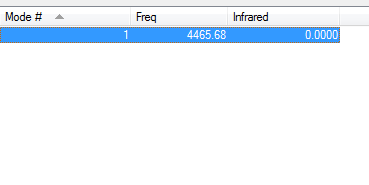
Vibrations of H2 in IR spectrum

Since Hydrogen is linear, the 3N-5 rule is followed and 1 vibrational mode is predicted. This is the stretching frequency at 4465.68 cm-1. This is a very high frequency since hydrogen atoms and small and thus the hydrogen bond is strong. Like nitrogen, hydrogen has no net dipole moment and therefore has zero intensity in the IR spectrum.

Bond Length

The H-H bond length is 0.74279 Angstrom. It is a linear molecule, and like nitrogen, has no net dipole since it is symmetric.

Haber-Bosch Reaction Energy

Reaction Energy for formation of Ammonia
N2 + 3H2 -> 2NH3
E(NH3) -56.55776873 a.u.
2*E(NH3) -113.1155375 a.u.
E(N2) -109.52412868 a.u.
E(H2) -1.17853936 a.u.
3*E(H2) -3.53561808 a.u.
ΔE=2*E(NH3)-[E(N2)+3*E(H2)] -0.0557907 a.u.

= -146.5 kJ mol-1

The enthalpy of formation of ammonia is -45.73112 kJ mol-1- from this information, the formation of 2 moles of ammonia would be 91.46 kJ mol-1.[1] [1] This is smaller than the Gaussian value of -146.5 kJ mol-1- this is due to the fact that the conditions used in Gaussian are different from actual experimental conditions. Since the reaction is exothermic, it can be seen that the formation of ammonia is favoured, over the formation of its gaseous reactants (N2 and H2).

Chlorine

Summary of Results

Calculation method: RB3LYP
Basis Set: 6-31G(d,p)
Final Energy E(RB3LYP): -920.34987886 a.u.
RMS Gradient Norm: 0.00002948 a.u.
Point Group: D∞H


Item Table from log file

Item               Value     Threshold  Converged?
 Maximum Force            0.000051     0.000450     YES
 RMS     Force            0.000051     0.000300     YES
 Maximum Displacement     0.000143     0.001800     YES
 RMS     Displacement     0.000202     0.001200     YES

The Cl-Cl bond length is 2.04176 Angstrom, and the molecule is linear.

Chlorine molecule


View the log file here: File:MP CL2 OPTF POP.LOG

Vibrations of Cl2 in IR spectrum


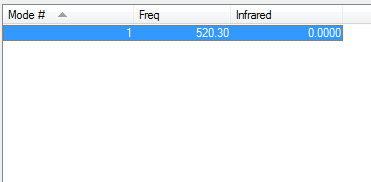
Chlorine follows the 3N-5 rule and 1 vibrational mode is predicted. This is the stretching vibration at 520.30 cm-1. This frequency is small since Chlorine atoms are big and the bond length is large. Like the other diatomic gases, chlorine has no net dipole moment.

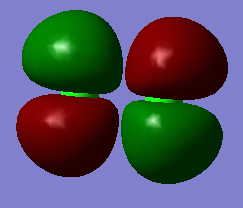
Molecular Orbitals in Chlorine

M.O.s in Chlorine
Orbital Description
- This M.O. is a sigma bonding orbital.

- This is formed by the overlap of the 3s orbitals of each chlorine atom.
- The A.O.s overlap in phase.
- The M.O. is lower in energy than the M.O.s formed by the overlap of 3p orbitals (all the M.O.s above)
- It has an energy of -0.93312.

- This M.O. is a pi bonding orbital.

- The two 3p orbitals overlap in phase.
- The p orbitals overlap "sideways". - The electrons are held above and below the plane of the bond, but not on the internuclear axis. - There is a nodal plane at the internuclear axis for all pi orbitals. - This has an energy of -0.40694

- This M.O. is a pi antibonding orbital.

- The two 3p orbitals overlap out of phase.
- "Sideways" overlap of p orbitals, nodal plane at internuclear axis. - This molecular orbital is the HOMO in molecular chlorine.
- This is higher in energy than the bonding orbital and has an energy of -0.31361.

- This M.O. is a bonding sigma orbital.

- It is formed as a result of "end to end" overlap of the two 3pz orbitals, i.e., along the internuclear axis, with the lobes pointing towards each other.
- The atomic orbitals overlap in phase.
- The orbital is higher in energy than the bonding pi M.O.s formed by the 3px and 3py orbitals.
- This is due to 'mixing' of the sigma bonding orbitals.
- Thus the energy of this molecular orbital is -0.47392
- This M.O. is fully occupied, and is the second HOMO after the pi antibonding orbitals (2pi*)

- This M.O. is the antibonding sigma orbital.

- The 3pz orbitals overlap along the internuclear axis ("end to end" overlap of the two 3pz orbitals with the lobes pointing towards each other)
- The atomic orbitals overlap out of phase.
- This orbital is unoccupied, and is the LUMO.
- It has an energy of -0.14207.



Mixing of Molecular orbitals:



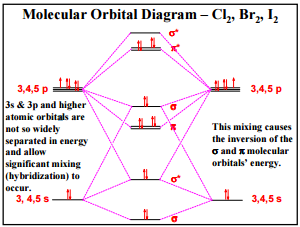
Figure 1 taken from http://web.utk.edu/~adcock00/g531ch17.pdf

As seen in the Molecular Orbital diagram, mixing occurs between bonding s and p σ orbitals when the two bonding orbitals are close in energy to each other. This is done to lower the energy of the lower energy sσ bonding orbital and to raise the energy of the higher energy pσ bonding orbital.[2] This is why one of the sigma bonding orbitals (formed from 3pz overlap along the internuclear axis) is higher in energy than the pi bonding orbitals (formed by 3px orbitals and 3py orbitals). Mixing allows greater orbital overlap and makes the formation of the molecule more exothermic.[2] [2]

References

  1. ↑ King, L. (1972). The enthalpies of ammonia ’ and formation, (January 1968), 675–683. (King, 1972)
  2. ↑ Inagaki, S., Fujimoto, H., & Fukui, K. (1976). Orbital mixing rule. Journal of the American Chemical Society, 98(14), 4054–4061. http://doi.org/10.1021/ja00430a006
Retrieved from "https://chemwiki.ch.ic.ac.uk/index.php?title=Rep:Mod:Mywiki&oldid=817558"